基于BP神经网络的长江口深水航道回淤量预测

王 淑 楠，顾 峰 峰，李 俊 花，赵 德 招

(1.上海海事大学 海洋科学与工程学院，上海 201306； 2.上海河口海岸科学研究中心 河口海岸交通行业重点实验室，上海 201201； 3.交通运输部长江口航道管理局，上海 200003)

0 引 言

长江口属于世界巨型河口，在径流、潮流等作用下，易形成由细颗粒泥沙组成的高浑浊带，垂向水沙盐分布的分层特征显著、近底含沙量高，使得长江口深水航道的回淤强度较大[1]。长江口深水航道治理工程于2011年5月18日通过国家竣工验收，发挥了巨大的经济效益和社会效益。然而，航道回淤量大、时空分布高度集中的难题也较为突出，给航道管理及维护施工调度(月度)带来巨大困难，因而如何精准预测航道回淤量是一个重要技术难题。

航道回淤量预测的方法通常包括：现场资料分析法、物理模型试验法、数值模拟法等。数值模拟法目前应用最为普遍，大多数学者采用的是三维水沙盐数值模型，例如王奎峰[2]等采用三维HEM-3D数值模型对黄河三角洲海域流场变化、盐度等进行了数值模拟，模拟结果与卫星遥感解译的岸线变化基本一致。吴修广[3]等应用FVCOM建立了三维潮流泥沙数学模型，成功再现了杭州湾潮流泥沙运动的过程。但数值模拟法在实际应用中还存在一些问题，如关键性泥沙参数的精确取值和整体模拟精度不高等[4]。随着各种工程技术领域研究的不断深入，人工智能的优势逐步体现。人工神经网络(Artificial Neural Network，ANN)是由大量简单神经元互联组成的非线性的信息处理系统，经过多年的发展，目前已有上百种的人工神经网络模型被提出[5]。常用的神经网络方法有误差反向传播算法(Back Propagation，BP)[6]、自适应共振理论ART(Adaptive Resonance Theory，ART)[7]、Hopfield网络[8]以及卷积神经网络(Convolutional Neural Nerworks，CNN)[9]等数十种。其中，BP神经网络在所有神经网络模型中应用最为普遍，被广泛应用于水沙研究的预测当中。例如：Deibel等[10]利用神经网络对鹿特丹港区航道进行泥沙预测，建立了以波浪、流量、沉降势能为输入参数，含沙量为输出参数的BP神经网络模型；霍粤蓟[11]运用BP神经网络以不同风力的风的作用时间作为输入参数、航道回淤量作为输出参数，建立了港口航道淤积分析模型。以上研究结果表明BP神经网络具有优异的多因子非线性逼近能力和较高的计算精度。

长江口深水航道维护一般以月为时段安排施工力量，月度回淤强度大且时空变化明显，导致如何精准预测航道回淤量成为了一个重要技术难题。人工神经网络预测模型的优点在于具有多因子耦合作用下针对关注目标快速的非线性拟合和预报能力。因此，本文在长江口航道淤积机制分析的基础上，建立了基于BP神经网络的航道回淤量预测模型，对逐月、逐个疏浚单元的回淤量进行训练、验证和预测，并优化预测模型。与文献[10-11]不同的是，本文并不是直接应用已有的传统泥沙冲淤理论，而是在此基础上根据长江口航道实际回淤机理筛选确定了多个导致长江口航道局部超强度淤积的主要影响因子作为神经网络的输入参数来建立一种新的映射关系，以实现高效率和高精度的预测。所以，在工程及河势边界相对固定，施工管理方法也相对固定的条件下，该模型可根据各河段实际回淤机理确定具体影响因子来预测月度内的航道淤积情况，并且模型预测结果也将为航道维护的科学管理和疏浚船舶的合理调度提供参考。

1 长江口航道淤积主要影响因子选取

长江口深水航道位于长江入海口，航道回淤影响因子众多，潮汐作用、长江径流、台风等恶劣天气都会造成航道淤积现象。目前关于长江口航道回淤特征已有很多学者进行了相关研究[12-14]，得到回淤总量巨大、回淤部位集中、以洪季回淤为主的回淤特征。孙继涛[15]发现由边滩进入航道的浮泥是长江口深水航道淤积的最重要来源；徐俊杰[16]发现导致长江口北槽航道回淤的主要原因是高床面切力引起的强再悬浮和泥沙沉降造成的高浓度近底含沙量；金镠[17]研究发现近底高浓度水层的横向运动对航道回淤起着重要作用；戚定满等[18]发现在航槽内部近底可观察得到存在可达上百公斤“超高”浓度泥沙层。因此，“超高”浓度泥沙层是导致航道局部超强度的主要原因之一。而近底高浓度泥沙层的形成与该区域多种宏观和微观作用机制密切相关。根据相关研究可知[18-20]，长江口航道回淤机制的主要物理过程可以描述如下。

(1) 在径潮流和波浪等作用下，长江口泥沙起动，形成长江口航道泥沙供给的来源。

(2) 北槽中下段航道底部的水沙净向下输运能力受径潮流及盐水入侵压力的影响，在一个潮周期内通常无法将高浓度底部泥沙团完整输运出北槽，造成泥沙往复振荡输运，汇聚槽内形成近底高浓度泥沙场。

(3) 北槽中下段区域受泥沙沉降和密度制紊的影响，泥沙在洪季易形成近底层高浓度，并主要以近底层高浓度的形式输运。

(4) 不同的潮位下，涨潮时期北槽中下段部分水沙越过南导堤进入航道，增加航道内泥沙供给，形成槽内近底高浓度泥沙场的重要泥沙来源。

(5) 在不同的动力、航道水深及沉速下，近底泥沙形成航道淤积。

综上可知，长江口深水航道回淤的外部主要因素可梳理包括如下：径潮流输运、盐水入侵、浮泥运输、泥沙絮凝沉降、风浪紊动等。其中径潮流输运、浮泥运输和盐水入侵主要对应潮位、潮差、流量和水深等影响因子；泥沙絮凝沉降对应水温影响因子；风浪、紊动对应波能影响因子等，其主要的对应关系如图1所示。在剔除相关度较高的影响因子后，筛选获取长江口航道淤积的主要影响因子为如下6个：上游流量、潮位、潮差、水温、水深和波浪。上述几个因子基本涵盖了径潮流驱动下的水沙输运、泥沙起动沉降、风浪影响等宏观和微观的回淤机制对航道回淤的影响。由于本文尝试建立一种外部水文条件与航道回淤量的间接映射关系，其中含沙量、泥沙粒径、水动力等直接影响因素受上述6个主要的外部水文条件影响，因此模型建立时不把直接影响因素作为本文模型的计算因子；且本文模型利用大数据的数据量大、易于获取的特点，以达到在大量实测水文数据的基础上进行模型预测的目的。因此，本文尝试进行一种可以表征外部水文条件与航道回淤量之间的间接映射关系的神经网络预测模型的构建方法和应用研究。

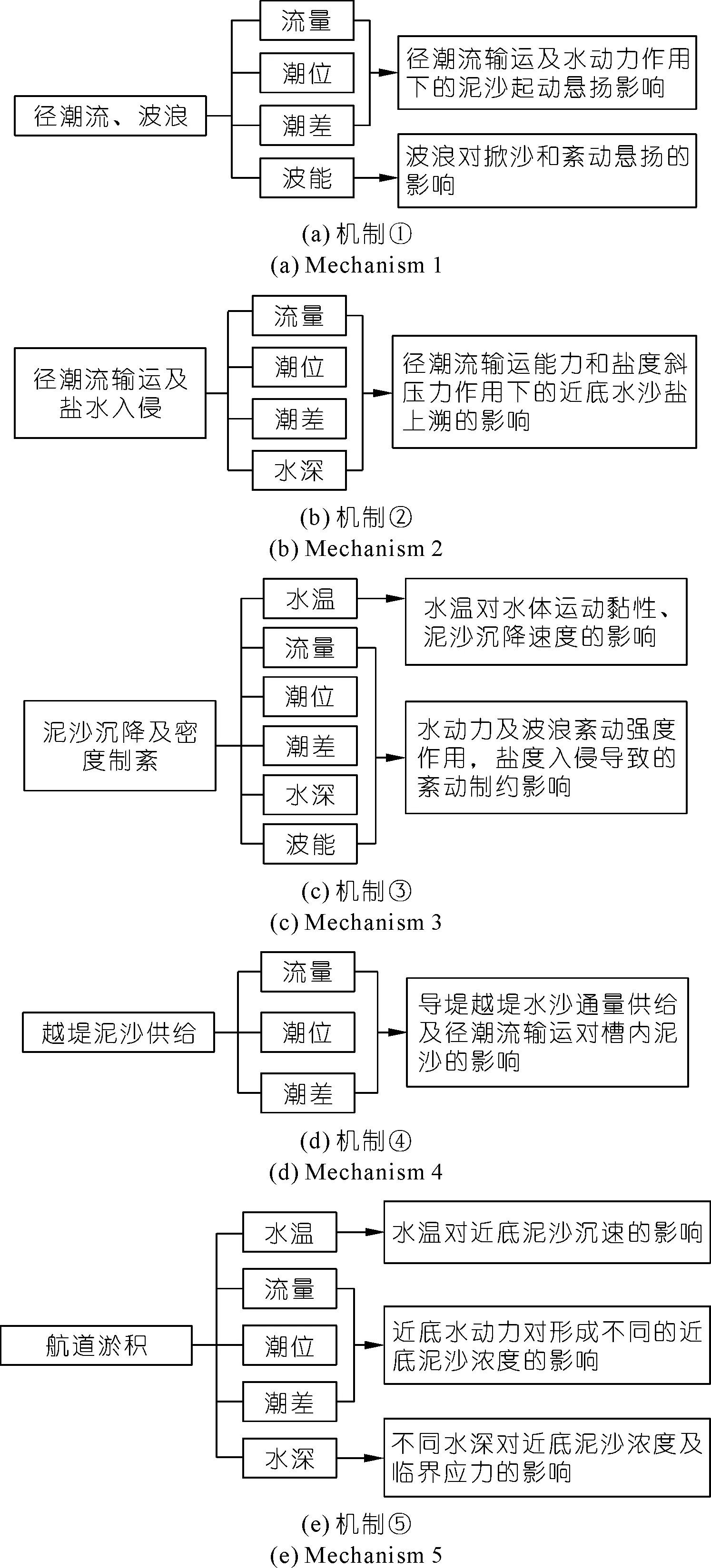
图1 影响因子及影响因子对应的回淤机制Fig.1 Influence factors and back siltation mechanism corresponding to influence factors

2 研究区域概况与资料说明

长江口共有北支、北港、北槽、南槽4个入海通道(见图2)，北槽是长江口的主要入海通道。目前长江口下段及口外呈“南汇东滩-南槽-九段沙-北槽-横沙浅滩-北港-崇明东滩-北支”滩、槽相间的格局。本次模型预测的分析数据主要来源于3个水文站：大通站、北槽中站、牛皮礁站，各个站点位置分布见图2。为降低航道回淤量，2015年11月实施了南坝田挡沙堤加高工程(+3.5 m)，南坝田挡沙堤加高完善工程(+4.5 m)于2019年12月实施。在此期间工程及河势边界相对固定，施工管理方法也相对固定，回淤量也较为稳定，维持在5 332万～5 550万m3之间，因此收集2016～2019年的资料用于预测和验证月度内的航道淤积情况。其中流量采用大通水文站数据，潮位、潮差、水温采用北槽中站数据，波高采用牛皮礁水文站数据，即用这6组数据分别代表航道回淤量变化的6个主要影响因素。

图2 长江口水文波浪观测系统站点布置Fig.2 Stations layout of hydrological wave observation system in the Yangtze Estuary

上游流量采用长江口上游潮临界区域的水文站——大通站的数据，通过水利主管部门的公开数据获取。北槽中站的水温、潮位、流速，牛皮礁站的波高及其对应的长序列数据，通过“长江口水文波浪观测系统”获取，该系统数据通过现场实时采集和内业实时接收，采集数据时间间隔一般为10 min。本次分析数据中，测量仪器问题导致2018年12月24日至2018年底的潮位以及2018年8～9月牛皮礁站波高及周期的部分数据缺失，模型计算时采用线性插补。航道水深采用“长江口深水航道考核测量水深”数据，由长江口航道管理局每月收集一次，取临近测次航道加密测量水深统计的航道单元平均值。

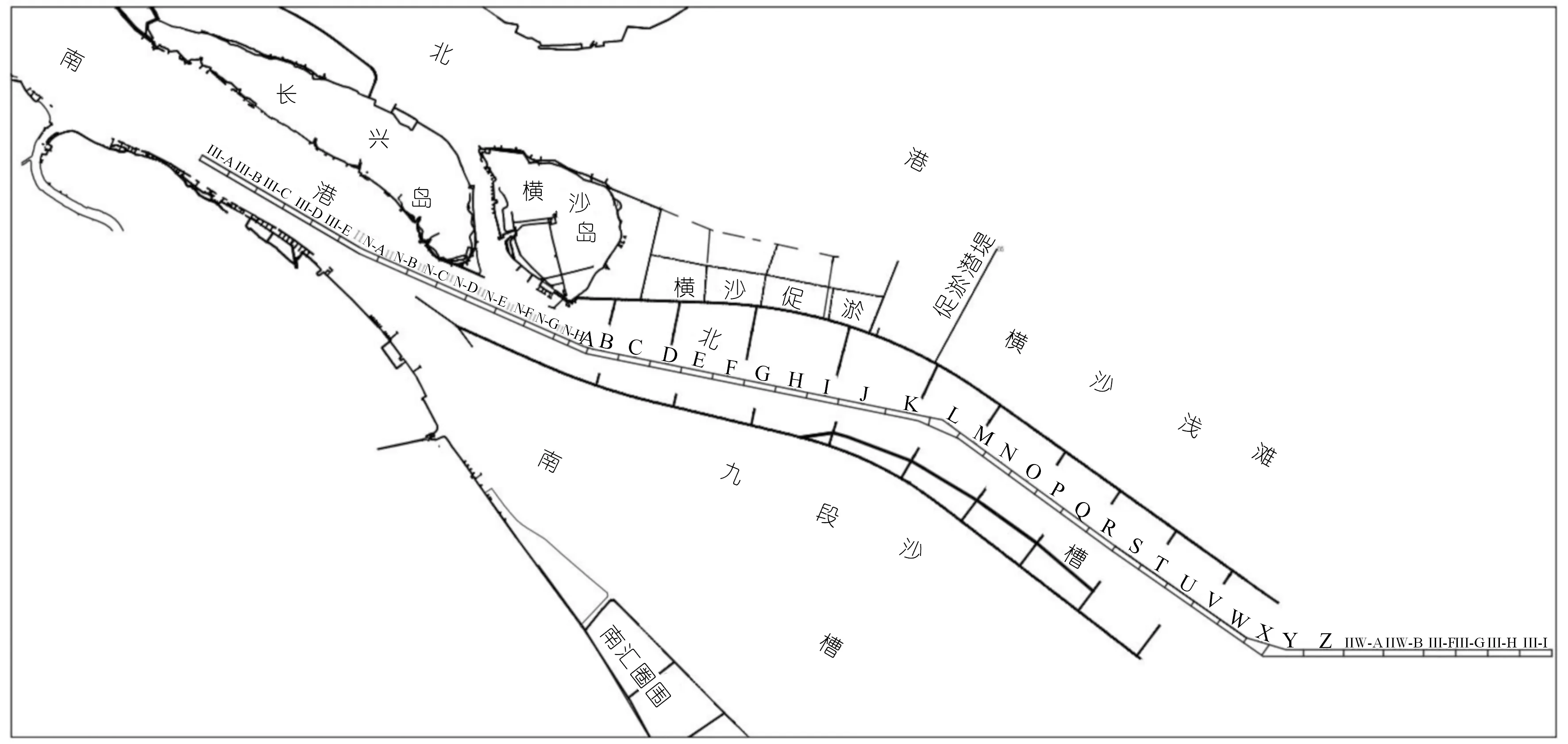
图3 长江口深水航道疏浚单元位置及主要单元布置Fig.3 Location of dredging units and layout of main units of deep-water channel in the Yangtze Estuary

基于上述数据资料，按月整理历年资料，分别为：上游代表站点的月度平均流量Qm(m3/s)，航道纵向中部位置代表站点处的平均水温Tm(℃)，航道纵向中部位置处代表站点处的平均潮位Hm(m)，航道纵向中部位置处代表站点处的平均潮差ΔHm(m)，航道单元水深Di，m(m)，m=1，2，…，M，M为以月为单位的统计数据总数，航道下段代表站点处的波能Em(kW·h/m)，其中波能E代表波浪能量的指标，其计算公式如下[21]：

(1)

式中：H为波高，m；k为波数，个；h为水深，m；σ=2π/T为波浪圆频率，s-1；T为波周期，s；g为重力加速度，m2/s。其中波高和周期为“长江口水文波浪观测系统”的实测数据，其中计算波能时，波高选取大于1.5 m进行计算。考虑上游径流传递和波浪影响与泥沙落淤之间存在一定的滞后性，本次研究经计算比对，选择提前7 d的实测资料进行统计。

由于历年的航道回淤量统计本身就是以月和航道单元进行统计，因而可以直接使用，但因航道单元的回淤量波动较大，个别数据存在异常值，所以需对回淤量数据进行平滑预处理。平滑处理采用smooth移动平均滤波函数，并选用lowess线性最小二乘滤波法。经过预处理后可以减小回淤量波动和回淤量预测误差。航道单元水深每月底按单元进行一次测量，在模型的训练和预测过程中使用前一个月的月底水深来预测月底的回淤量。

3 基于BP神经网络的航道回淤预测模型

3.1 模型基本原理

神经网络(Artificial Neural Network，ANN)是一种旨在模仿人脑结构及其功能的信息处理系统[22]。神经网络有很多种，用途各不相同，常用的有前馈神经网络、自组织网络、BP神经网络等。BP神经网络是一种根据误差反向传播算法训练的多层前馈神经网络，它主要由输入层、隐含层和输出层3部分组成，具有较强的非线性映射能力、自学习和自适应能力、泛化能力、容错能力[23]。

BP神经网络各层神经元阈值和网络权值的确定，是一个需要不断调整的过程，该过程主要通过BP算法来完成，更新过程主要包括网络信息输出的正向传播和误差的反向传播两个阶段。将每组输入信号的输出值和期望输出值进行比较，如果满足精度要求，则网络训练结束，如果不符合精度要求，那么开始误差反向传播。由于BP神经网络具备简单直观的网络结构和可以无限逼近任意函数的能力，可以提升多因子作用下回淤机制研究能力，提高航道回淤预测的效率和精度，所以本文选择BP神经网络作为本次研究的网络模型。

3.2 模型构建

模型网络结构见图4。针对每个航道单元，输入层为xij，输出层为uij，输入层与隐含层各神经元之间的连接权重为wik，隐含层与输出层各神经元之间的连接权重为wkp，下标i、k以及p分别表示输入层、隐含层以及输出层神经元的个数，下标j表示样本数。其中BP神经网络预测模型设置的输入变量为6个，输出变量为1个，也即航道回淤量，具体参数见表1。该模型采用的激活函数为traingdm，网络的其他参数为：学习速率h=0.01，训练次数epochs=1 000，目标误差goal=10-6，训练步长show=25。

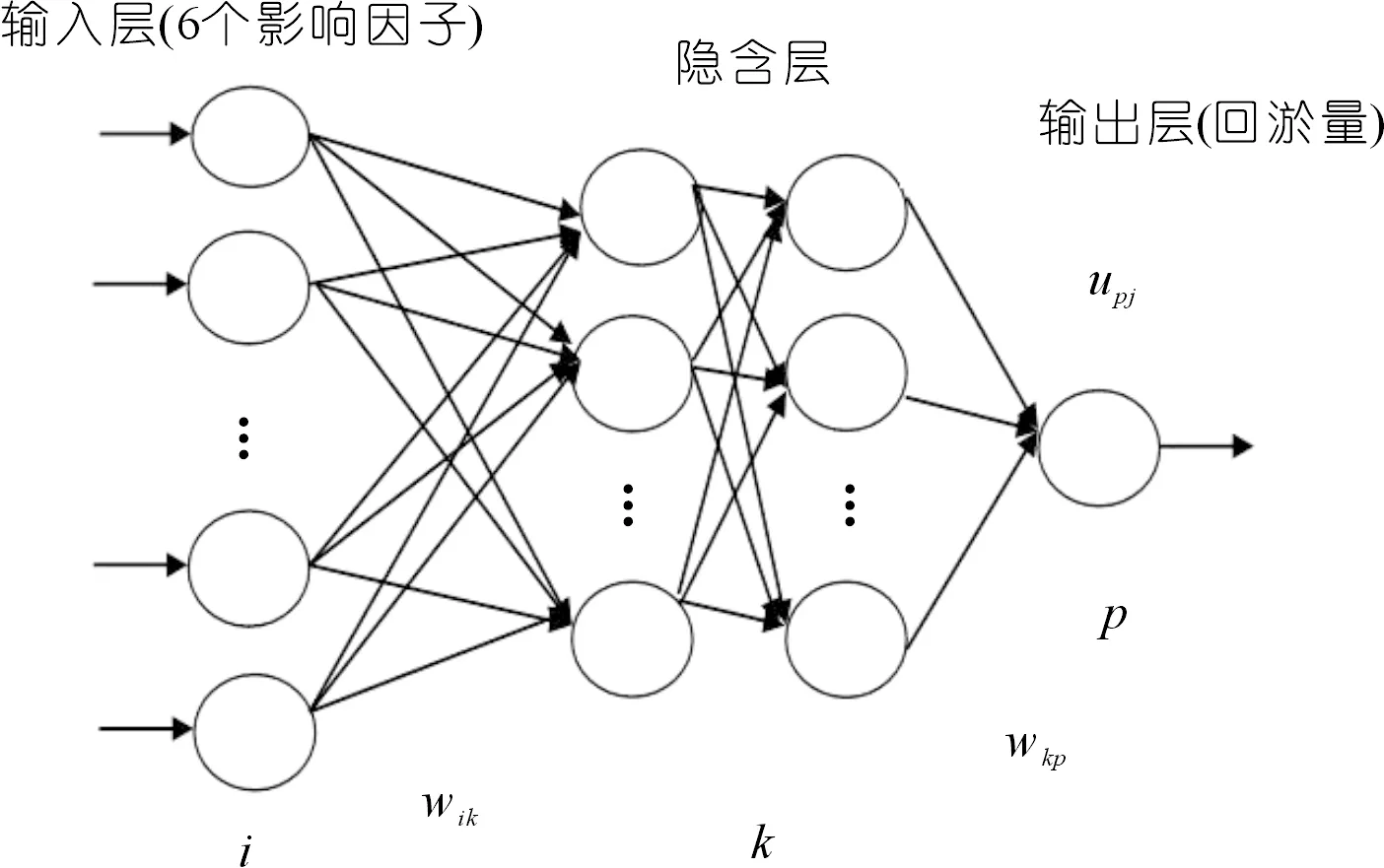
图4 回淤量预测的网络拓扑结构Fig.4 Network topology of back siltation prediction

表1 神经网络模型参数Tab.1 Parameters of neural network model

对一个含有隐含层的BP神经网络来说，隐含层的层数以及神经元数量会影响BP神经网络的性能。所以选择恰当的隐含层个数以及神经元数量对于神经网络模型十分重要。目前被广泛用来确定隐含层节点数目的公式为[24]

(2)

式中：l为隐含层节点数；m，n为输出层与输入层的节点数；a的范围为[1，10]。

在上述神经网络结构的基础上，建立基于神经网络的回淤量的预测模型，并进行训练和验证。本次模拟预测的步骤如下：① 根据收集的2016～2019年各水文站数据资料和实测资料，建立航道回淤预测的神经网络数据库，并对回淤量进行标准化处理(转换成单元淤积强度)；② 构建网络结构并确定BP神经网络模型的基本参数；③ 利用2016～2018年的数据对网络进行训练，以每一个航道单元、每一个月的回淤量作为训练目标，以每一个月相应的水文条件及实测的航道单元水深作为输入因子，即可完成神经网络的训练；④ 利用2019年的数据对网络进行预测验证，分析预测结果精度和模型可靠性。

3.3 网络模型优化

为找到最佳的隐含层层数以及神经元个数，通过比较训练网络与预测网络的46个航道单元的模拟值与实测值之间的Pearson相关系数(R)的平均值来完成。R的计算公式如下：

(3)

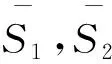
表2列出了不同隐含层及不同神经元数目下模型的R值，其中预测网络R值包括空间上的46个航道单元的R值平均值和时间上12个月各航道单元总回淤量的R值平均值。综合比较训练网络和预测网络的R值发现：隐含层层数为2层时训练网络的结果较1层时稍好。其中预测网络的各航道单元R值平均值较其他3组R值偏小，是由于46个航道单元的上段和下段中的一些单元R值过小，导致R值平均值偏小，网络预测精度偏低，但从预测网络的航道总量R值来看，可以达到0.8左右，可以用于回淤量预测模型当中。因此，综合考虑训练网络和预测网络的R值，网络规模为[6，20，20，1]的表现最佳，所以最终使用的训练和预测网络的隐含层数为2层，且各层神经元分别为20个。

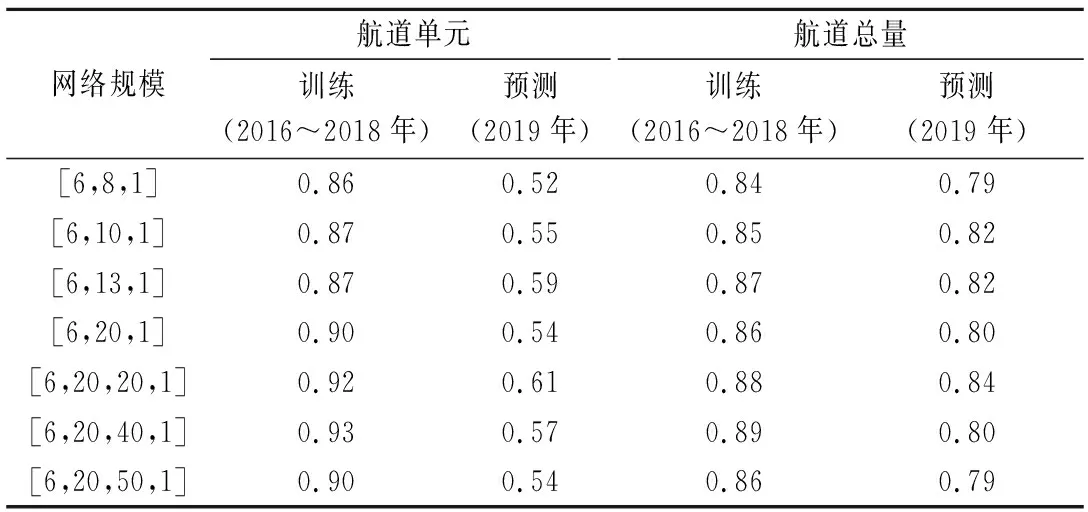
表2 不同隐含层及不同神经元数目下模型的R值Tab.2 R value of model under different hidden layers and different number of neurons

3.4 网络模型的训练结果分析

(1) 典型航道单元的回淤量拟合结果分析。选取2016～2018年3 a数据的拟合数据，并选取航道的上、中、下3段的典型单元，拟合结果参见图5，训练得到的各区段回淤的相关系数基本在0.78以上，其中航道中段训练结果最好，上段和下段根据前述可知其回淤量绝对值较小，实测数据误差影响较大，导致训练结果比中段稍差。这里回淤量为负表示航道淤积，正为冲刷，下同。

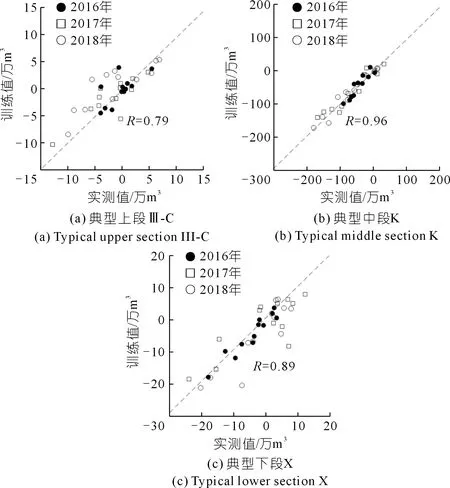
图5 不同航道单元月度回淤量预测和实测对比Fig.5 Comparison of monthly back siltation prediction and actual measurement of different channel units

(2) 月度回淤总量及洪枯季典型月份的回淤量分布拟合结果分析。月度航道回淤总量的拟合结果参见图6(a)，可以看到，2016～2018年各月回淤总量拟合结果很好，R值可达0.98。另外，选取洪枯季代表月份(2月和8月)的各航道单元回淤量拟合结果进行分析，结果见图6(b)和图6(c)。可以看到，洪枯季的总体拟合度都较高，其中洪季(R=0.97)的训练拟合的结果明显优于枯季(R=0.76)。

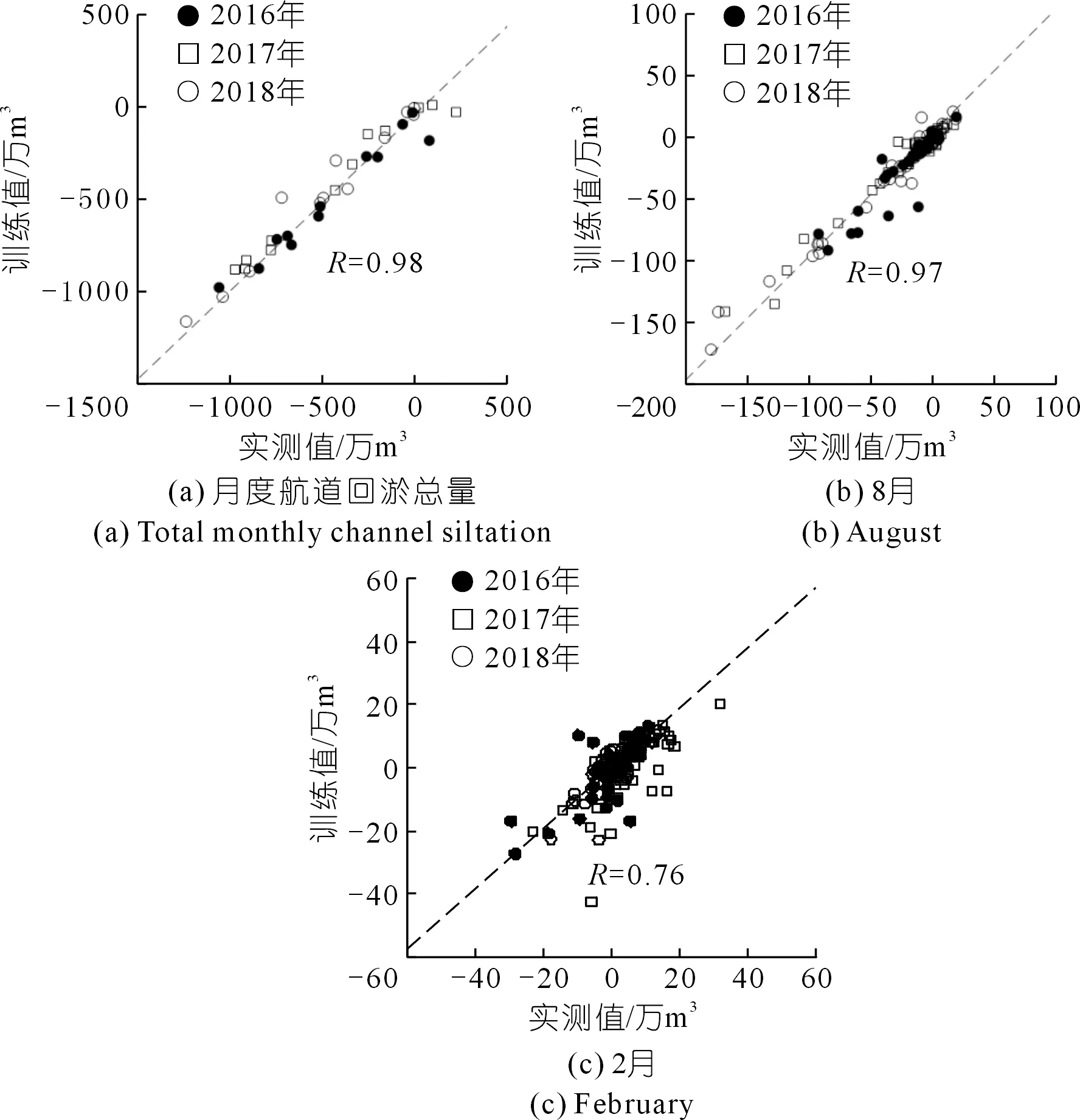
图6 月度航道回淤总量及洪枯季典型月各单元回淤量训练值和实测值对比Fig.6 Total monthly channel back siltation amount and the comparison of the training values and the measured values of monthly siltation amount of each unit in a typical flood and dry season

3.5 网络模型的预测结果分析

以2019年航道回淤量作为模型验证和误差分析目标，预测模型的各航道单元月度回淤量的实测与预测对比见图7(a)，月度航道总量的预测结果与实测的对比情况见图7(b)。

结合2019年回淤量实测数据和图7(a)拟合图可知，中下段的航道单元K～W回淤量较大，其预测精度明显高于回淤量较小的上段航道单元并且航道单元的月度回淤量实测值与预测值拟合点基本分布在Y=X线附近。而上段和末段回淤量绝对值较小，实测数据误差影响较大，并且存在个别异常数据，导致上段航道单元的拟合程度不好。

由图7(b)可知，预测月度航道回淤总量变化趋势与实测基本一致，较好地反映了月度航道回淤总量的年内变化特征，其各月统计结果的R值基本在0.70以上，洪季可以达到0.90。

图7 2019年实测与预测值比较Fig.7 Comparison chart of measured and predicted back siltation values in 2019

2019年洪枯季典型月的航道各单元回淤量预测值和实测值比较参见图8，全航道年总量预测结果及误差统计见表3。由图表可知：① 洪枯季典型月份各航道单元的回淤量预测的结果具有较高的精度(洪季典型月R值为0.91，枯季典型月R值为0.78)，反映出航道回淤量时空差异和分布规律：洪季淤积高于枯季，淤积部位集中在H～O单元。② 整体上来看，年回淤总量预测误差较小，仅为4.13%。上述误差分析结果证明了本文选取的影响因子及构建的预测模型的合理性，验证了本文建立的模型在回淤总量和回淤量较大的航道单元的预测上效果较好，可以用来进行航道回淤的预测当中。

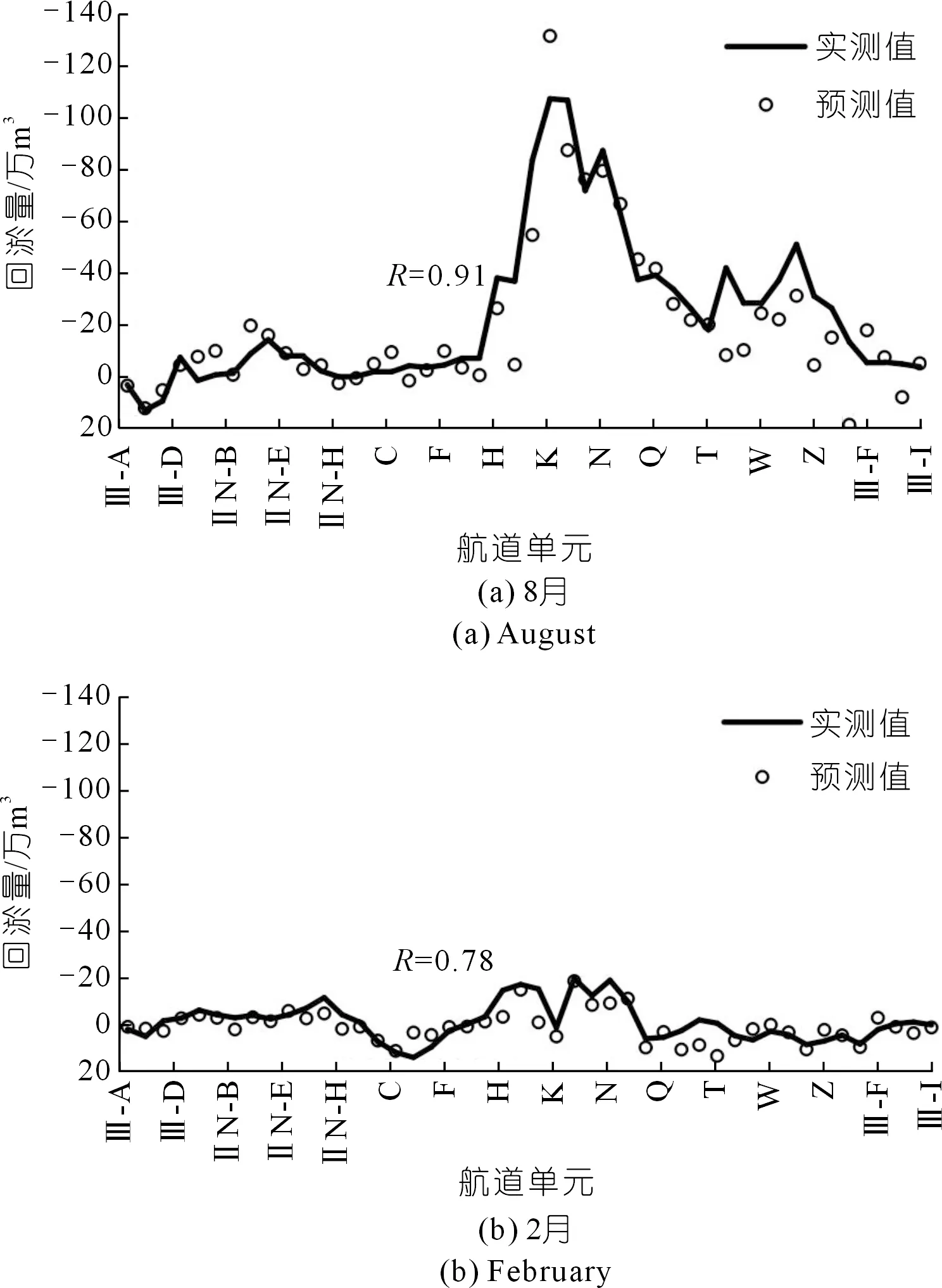
图8 2019年洪枯季典型月的航道各单元回淤量预测和实测对比Fig.8 Comparison of predicted and measured back siltation volume of each channel unit in typical months in flood and dry seasons of 2019

表3 2019年航道回淤量总量实测与预测比较Tab.3 Comparison of measured and predicted total amount of back siltation in 2019

3.6 回淤参数敏感性分析

模型参数敏感性分析能够确定参数对模型输出的重要性及贡献度，以便有针对性地优选较为重要的参数。本文采用局部分析法对6个参数进行敏感性分析，将6个输入参数上下变动10%，计算回淤量的变化情况。本文使用相对敏感性值将参数敏感性归一化，计算敏感性指数I[25]：

(4)

式中：O为模型模拟输出结果；Fi为影响O的因子(参数)；ΔO为模型模拟输出结果的改变量；ΔFi为表示影响O的因子(参数)的改变量。根据I，可将敏感性进行分类(见表4)。

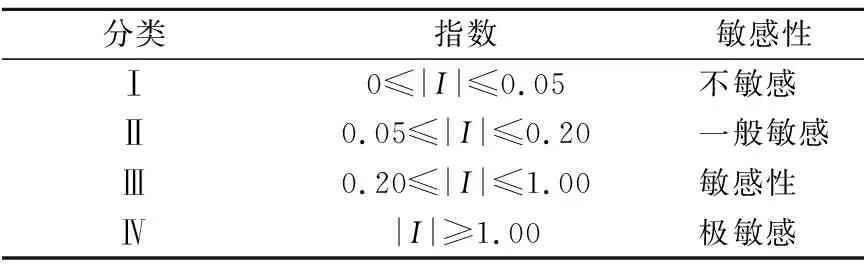
表4 参数敏感性分类Tab.4 Classification of parameter sensitivity

应用式(4)计算2019年全航道46个单元各参数的敏感性指数并进行对比，结果见表5。表5中初值、回淤量改变量、敏感性指数|I|均为12个月的平均值。由表5可知各参数敏感性排序为：水深>潮差>潮位>流量>水温>波能。其中水深的敏感性指数最大，说明水深因子对全航道的回淤量影响最大。并且所有参数敏感性指数|I|均大于1，因此各参数敏感性等级均为Ⅳ级，也说明了前文在回淤影响因子上选取以及模型构建的合理性。

表5 参数敏感性分析结果Tab.5 Results of parameter sensitivity analysis

4 结论及展望

(1) 本文构建的预测模型对航道不同区段单元的回淤量、月度回淤总量及洪枯季典型月份的回淤量分布都具有较高的拟合精度。

(2) 中下段航道单元的月度回淤量实测值与预测值拟合程度较好，上段航道单元拟合程度稍差。

(3) 预测月度航道回淤总量变化趋势与实测基本一致，较好地反映了月度航道回淤总量的年内变化特征，其各月统计结果的R值基本在0.70以上，洪季可以达到0.90。

(4) 洪枯季典型月份各航道单元的回淤量预测的结果具有较高的精度(洪季典型月R值为0.91，枯季典型月R值为0.78)，反映出航道回淤量时空差异和分布规律。

(5) 整体上来看，年回淤总量预测误差较小，仅为4.13%。

(6) 通过对回淤影响参数进行敏感性分析得到全航道各参数敏感性指数排序为：水深>潮差>潮位>流量>水温>波能。

上述研究结果证明了本文选取的影响因子及构建的预测模型的合理性，同时验证了模型在回淤总量和回淤量较大的航道单元和月度的预测上效果较好，在回淤量较小的航道单元预测精度上稍差，在之后的研究中可以增加几年的水文数据，增大训练数据容量，进一步提升预测精度。在工程及河势边界相对固定，施工管理方法也相对固定的条件下，该模型可根据各河段实际回淤机理确定具体影响因子来预测月度内的航道淤积情况，模型预测结果可为航道维护的科学管理和疏浚船舶的合理调度提供重要支撑。在后续工作中，可以进一步分析不同区域的回淤受各因子的影响，从而获取具体准确的回淤机理。