2022年低枯水期长江中下游水位流量关系外延研究

蒋 四 维，吴 琼，贺 志 岗，周 文 静，张 亭，陶 昕 怡

(1.长江水利委员会水文局 汉江水文水资源勘测局，湖北 襄阳 441000； 2.长江水利委员会 水文局，湖北 武汉 430010)

0 引 言

2022年汛期受持续高温少雨和上游来水不多等因素的影响，长江流域罕见地出现“汛期反枯”现象。8月份以来，长江干流及洞庭湖、鄱阳湖水位均为有实测记录以来同期最低[1]。为缓解旱情、保障用水安全，预测准确可靠的低枯水期水位流量关系，从而调度三峡水库向长江中下游补水，需对长江中下游典型水文站当前水位流量关系曲线进行低枯水延长，寻找合理的水位流量关系曲线延长趋势至关重要。

目前国内对于水位流量关系曲线延长的研究，聚焦于利用多种方法进行高水外延，除传统方式[2-4]外，刘文忠[5]提出利用Matlab平台编制曼宁公式或史蒂文法进行高水外延；程银才[6]、李明华[7]等采用多层递阶和回归分析相结合的方法对单一水位流量曲线进行外延。李正最等[8]在断流水位分析法的基础上以0.618法和二次插值法对断流水位进行优选；付晓忠等[9]在水位流量单一关系曲线延长中采用水位面积、水位流速关系曲线法和分析法进行低水外延。但是这些分析法受到分析者主观认知差异的影响，难以确定最优断流水位，且水位流速关系曲线延长目前多采用顺势延长，任意性较大。基于此，本文提出用一元三点插值法对顺势延长水位流速关系曲线进行验证，同时在分析长江中下游代表站点低枯水期比降及糙率资料的基础上，结合水文资料整编规范，将曼宁公式作为低枯水期水位流量关系曲线延长的一种新的参证方式，用以弥补传统低枯水外延方式的不足。

1 低枯水期水位流量关系外延方法

在对测站低枯水期水位流量关系线进行外延时，通常参照水文资料整编规范，对水位面积、水位流速关系点比较集中的站采取水位面积、水位流速关系曲线法外延；对测站下游有浅滩、石梁且断面形状较为整齐的断面，采用断流水位法进行外延。由于曼宁公式是明渠稳定流经典公式，适用于水位流量关系稳定的河流断面，本文在上述两种方法外，也将曼宁公式作为水位流量关系曲线低枯水延长的一种方式。

1.1 水位面积、水位流速关系曲线法外延

根据水文资料整编规范，对于河床比较稳定，水位面积、水位流速关系点比较集中，曲线趋势明显的测站，可根据水位面积、水位流速关系曲线作高低水位延长。

水位面积关系延长通过实测大断面资料的不同水位级来判定左右水边，从而确定断面范围，提取各起点距下对应的测深垂线，并计算过水断面面积。计算时将相邻测深垂线、垂线间水面、河底构成梯形，以相邻垂线深度作为梯形的上、下底，垂线间水面宽度作为梯形的高，分别计算出每一部分的面积。其中，两岸边的部分面积按三角形面积计算，各部分面积的总和即为河道横断面面积。

部分面积计算[10-11]采用平均分割法，见图1(a)，以测深垂线为分界将过水断面划分为若干部分，相邻垂线之间的间距为部分宽，乘以相邻垂线水深的平均值，得到部分面积，见式(1)，岸边部分面积按三角形面积计算。

(1)

式中：Ai为平均分割法计算的第i部分面积，m2；i为测深垂线序号，i=1，2，…，n；Hi为第i条垂线的实际水深，m；Bi为第i部分宽，m。

过水断面面积为各部分面积之和，见式(2)。如果过水断面为复式断面，可分别计算各分块断面面积再求和。

(2)

通过上式计算出各水位级对应的面积后，绘出水位面积关系曲线，如图1(b)所示。

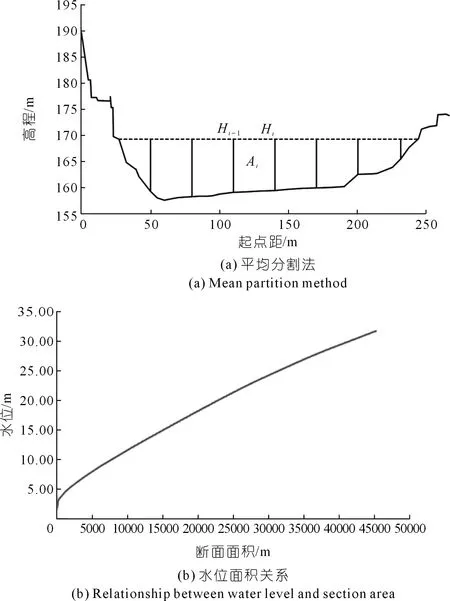
图1 水位-面积曲线绘制Fig.1 Water level-section area curve drawing

低枯水期水位流速曲线延长通常是顺着实测流量资料的关系趋势向下延长，此种方法在延长过程中存在一定的任意性。为探求顺势延长法关系曲线的合理性，本文提出在中低水选择3个以上有代表性测点，在水位-流速曲线上通过一元三点插值法[12-13]对低枯水期水位-流速进行验证。

对于一条水位流速曲线，断面平均流速用v表示，水位用Z表示，若选取N个结点(N>3)，水位Z对应的断面平均流速v用下式计算：

(3)

在水位流速关系曲线上，在端点附近与曲线曲率较大处选择至少3个水位级呈梯级分布的测点对低枯水期水位进行插值计算。

1.2 断流水位法外延

断流水位法[14]适用于测站下游有浅滩、石梁，或下游较长距离内河底平坦，断面形状较为整齐且无浅滩、分流等现象的断面。以断流水位为控制点对低枯水期水位作延长时，应以断流水位和流量为零的坐标(Z0，0)为控制点，将水位流量关系曲线向下延长至需要的水位处。断流水位的确定可采用下列方法：

(1) 根据测站纵横断面资料确定法。如测站下游有浅滩或石梁，则以其顶部高程作为断流水位；若下游较长距离内河底平坦，则以基本水尺面最低点高程作为断流水位。

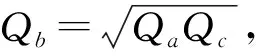
(4)

式中：Z0为断流水位，m；Za，Zb，Zc分别为水位流量关系曲线上a，b，c三点的水位，m。

图2 图解法确定断流水位Fig.2 Graphic method for determining stage of zero flow

1.3 曼宁公式法外延

曼宁公式适用于河道顺直、河床底坡平坦、断面均匀较稳定的测站，根据有无糙率和比降资料，可分别对流速或流速因子进行延长计算。

(5)

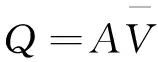
(6)

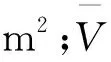
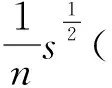
2 典型水文站枯水水位流量关系外延规律

通过对低枯水期水位外延方法得到水位流量延长曲线是一种理论手段，在实际应用过程中还需要参照具体测站的历年水位流量关系变化规律，来辅助验证低枯水期水位流量外延曲线的合理性。测站水位流量关系受工程建设、河道冲淤等多种因素的影响，在年际变化中往往呈现出一定的规律性。本文参考宜昌、沙市[15]、螺山[16-17]、汉口[18]、大通等典型站历年水位流量整编方法及各站的水位流量关系变化趋势，分析影响水位流量关系的因素，找寻变化规律，对低枯水期水位流量关系延长曲线进行进一步验证。

以汉口水文站为例，收集汉口水文站2009～2022年多年大断面对比图(见图3)及历年低枯水期水位流量关系曲线(见图4)。

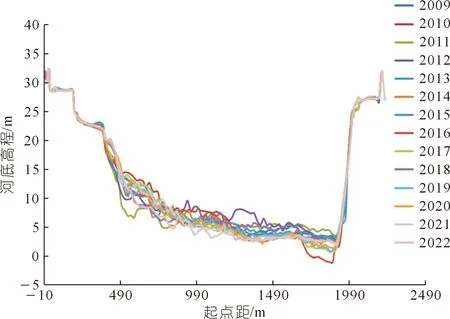
图3 汉口站多年大断面对比Fig.3 Comparison of multi-year cross-section of gauges in the Hankou hydrological gauge

图4 汉口站低枯水期水位流量关系Fig.4 Hankou hydrological gauge low-flow rating curve

由图3～4可知：汉口水文站同流量级水位年际变化处于下降趋势，而多年大断面对比图显示汉口水文站河底高程同样处于下降趋势，两种方法分析结果基本一致。以此得出汉口站受断面冲刷影响，同水位级下流量年际变化应持续偏大，水位流量关系曲线应持续向右偏移的结论。因此在对汉口站进行2022年低枯水期水位流量关系外延时，所得的延长曲线也应符合这一规律，低枯水期同水位级流量较往年偏大。

3 2022年“汛期反枯”时汉口站水位流量关系外延分析

汉口站2022年8月以来水位持续下降，相关单位共开展低水流量测验13次，施测范围9 260～20 900 m3/s，水位变幅6.21 m。在绘制水位流量关系曲线外延部分时，分别采用水位-面积、水位-流速关系曲线外延，断流水位法外延及曼宁公式法外延3种方式进行比较分析。

3.1 水位-面积、水位-流速关系曲线外延

通过2022年实测流量及大断面成果绘制水位-面积及水位-流速关系曲线，分别在两条曲线上查找水位所对应的面积、流速，两者相乘得到相应流量并进行外延。水位-面积根据部分面积法计算求得，水位-流速曲线综合顺势延长和一元三点插值法进行绘制(见图5)。

图5 水位流速曲线延长Fig.5 Extrapolation of water level-velocity curve

利用一元三点插值法外延过程中，以实测最低流速点为界限，在其附近以均匀水位间距选取几组数据，每组数据由3个结点构成，计算曲率，优选曲率最大处数据作为所求结点，以此延长水位-流速关系曲线。

汉口站水位流速关系延长过程中，在实测最低水位附近选取3组数据，如表1所列，经曲率计算，选择组1结点为参证数据进行低枯水期水位流量关系曲线外延，外延曲线结点如表2所列。

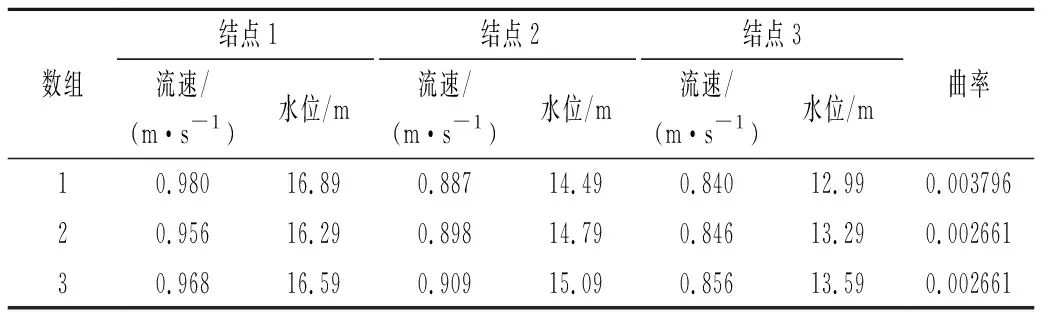
表1 结点选取Tab.1 Node selection

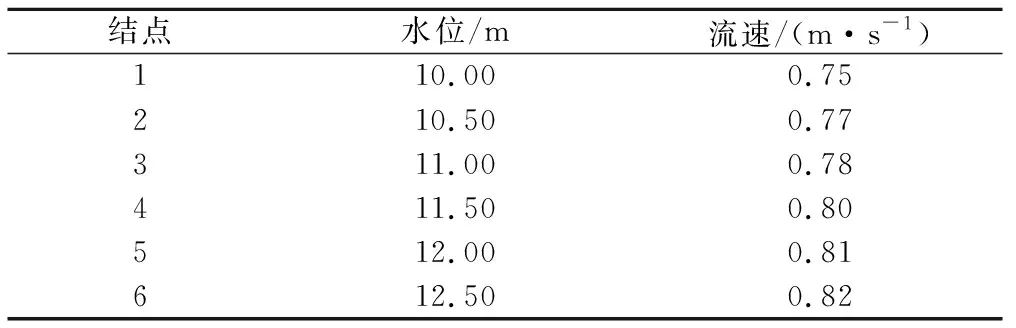
表2 一元三点插值法外延曲线结点Tab.2 Epitaxial curve nodes by single-variable three-point interpolation method

通过上述两种方式对水位-流速曲线进行外延，由图5可知外延趋势可靠合理。

3.2 断流水位法外延

采用断流水位分析法在汉口站水位流量关系曲线变曲处，找到点a(9 260 m3/s，12.72 m)，点c(20 900 m3/s，18.93 m)，通过公式(5)计算点b(13 900 m3/s，15.20 m)，从而算出断流水位点0(0，7.80 m)。

3.3 曼宁公式法外延

通过统计汉口站与上游石矶头水位站低枯水时期的水位落差，推算出低枯水期汉口站糙率稳定在0.024，两站区间比降稳定在0.000 025，根据2022年实测大断面资料计算各级水位下汉口站湿周及水力半径，从而推算流量如表3所列。

表3 利用曼宁公式进行低枯水期水位流量关系延长Tab.3 Low flow extrapolation by Manning′s equation

4 结果分析比较

通过3种不同方法对水位流量关系曲线进行外延，得到图6。

图6 不同分析方法得到的低水外延曲线对比Fig.6 Comparison of flow extrapolation curves during low water period with different analysis methods

将汉口站水位14.40 m(枯水)以下实测流量资料与查线流量进行对比，结果见表4。

表4 实测流量与查线流量相对偏差统计Tab.4 Relative deviation of measured flow and extrapolation flow

在判断水位流量关系精度时，除计算相对误差外，引入系统误差和随机不确定度两个概念，计算公式见式(7)～(8)，系统误差用以描述实测点相对于水位流量关系线的整体偏移情况，随机不确定度用以描述实测点相对于水位流量关系线的离散程度。通常某类站点采用ADCP进行流量测验，系统误差应在±1%以内，随机不确定度应在10%以内。3种方式精度统计见表5。

表5 外延方式精度统计Tab.5 Precision seatistics of extrapolation mode %

(7)

(8)

由表5可知，3种方法中通过曼宁公式法进行低水外延的偏差最少，将曼宁公式法外延曲线与历年水位流量关系曲线进行对照，结果见图7。

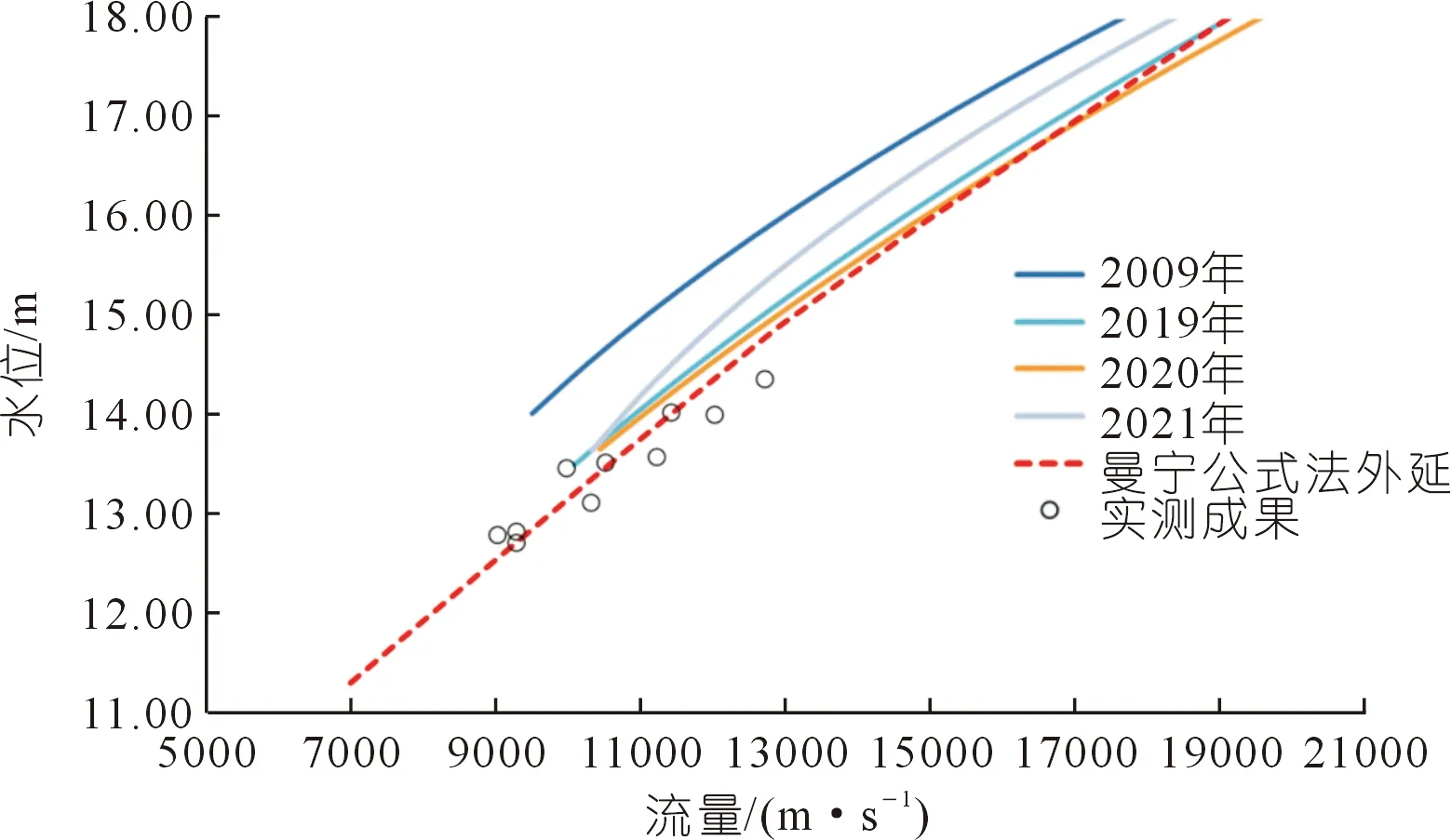
图7 汉口站2022年低枯水期水位流量关系曲线Fig.7 Water level-flow relationslip curve of Hankou station during low-dry season of 2022

根据水位流量关系变化趋势及曼宁公式，综合绘制2022年“汛期反枯”期间汉口站水位流量关系曲线，确定了各流量级对应水位，如表6所列。

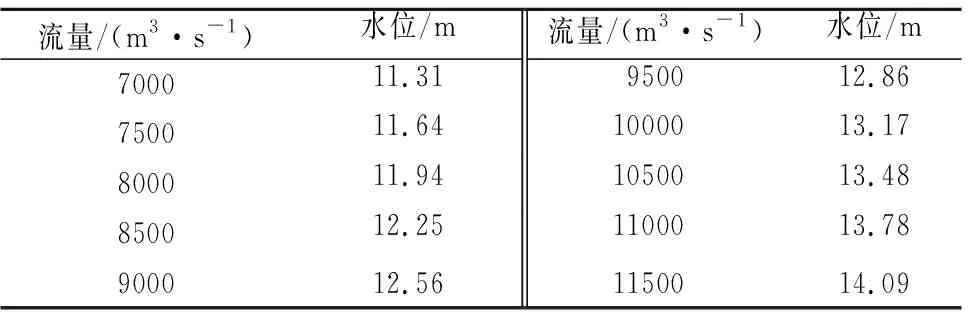
表6 汉口站各流量级对应水位Tab.6 Corresponding water level of each flow stage in Hankou hydrological gauge

此分析方式也适用于长江中下游其他站点枯水期水位流量关系曲线外延，如宜昌、螺山、九江、大通站可参照历年水位流量关系趋势及水位面积-水位流速曲线延长，沙市站可参照历年水位流量关系趋势及曼宁公式延长。

5 结 论

(1) 由于影响水位流量关系曲线精度的因素很多，因此进行低枯水期水位流量关系曲线延长时应该分析各种影响因素，尤其应重点分析历年水位流量关系曲线趋势以及多年大断面冲淤变化的合理性。

(2) 通过3种方式对低枯水期水位流量关系外延趋势进行分析，结果表明断流水位法因为特征点的确定受到分析者主观认知差异的影响，因而难以确定最优断面水位，精度相对较差。水位面积、水位流速关系曲线延长法精度普遍较高，适用于多数低枯水期水位流量关系稳定的站点，且一元三点插值法与水位流速关系曲线延长拟合程度较好；曼宁公式延长法则适用于河床稳定、各要素关系点比较集中、曲线趋势明显、低枯水期比降糙率趋近于常数的测站。

(3) 通过准确合理的水位流量关系曲线外延，可由水位变化趋势推算相应流量成果。本文获取的汉口水文站的低枯水期外延流量与实测成果偏差较小，在应对2022年长江“汛期返枯”现象中为长江流域旱情防御提供了参考。