抚河流域农业干旱的影响机制研究
2023-03-06郑金丽,周祖昊,刘佳嘉,严子奇,李国文,王钦钊
郑 金 丽,周 祖 昊,刘 佳 嘉,严 子 奇,李 国 文,王 钦 钊
(1.中国水利水电科学研究院 流域水循环模拟与调控重点实验室,北京 100038; 2.江西省水文监测中心(江西省水资源监测中心),江西 南昌 330002; 3.江西省水文局,江西 南昌 330000)
0 引 言
干旱是一种缓慢发生、影响范围大、持续时间长的自然灾害[1],在全球范围内均可发生,严重影响了全球粮食作物生产[2]。据《中国水旱灾害公报2020》统计,1950~2020年我国年均粮食损失高达163亿kg,年均受灾面积高达200万hm2[3]。因此,开展干旱研究对于减少农业干旱造成的损失至关重要。
农业干旱作为干旱灾害的主要类型之一,常通过建立干旱指数的方法进行评估[4-5]。已有农业干旱指数通常分为3种,即土壤水分指数类、作物生理生态指数类和卫星遥感干旱指数类[6],其中由于土壤水分是影响作物生长发育的主要因子,因此基于土壤水分的干旱指数被广泛应用[7]。周洪奎等[8]采用标准化土壤湿度指数反映黄淮海平原的农业干旱状况,发现干旱指数对农业干旱引起的冬小麦减产起到指示作用。Souza等[9]采用土壤水分农业干旱指数分析农业干旱与玉米和高粱作物的生产力和收获面积的相关性,发现农业干旱与高粱作物的相关性更加显著。Yao等[10]采用土壤水分亏缺指数分析农业干旱对小麦/玉米产量的影响,发现产量和干旱指数的相关性在6、7月最高。由于大面积土壤水分的监测比较困难,因此基于水文模型的农业干旱评估方法被广泛应用。如王富强等[11]构建基于SWAT(Soil and Water Assessment Tool)的区域农业干旱模拟模型;李军等[12]通过VIC(Variable Infiltration Capacity)模型模拟蒸散发、径流和土壤水分等水文气象要素构建农业干旱指数。但是土壤含水量受作物类型、灌溉条件等人类活动影响,而考虑灌溉等人类活动对农业水循环过程影响机制的模型不多,因此需要构建反映人类影响机制的水文模型对农业水循环过程进行模拟,在此基础上对农业干旱进行评价。
农业干旱受到很多因素的影响,其中气候变化和人类活动是主要的影响因素[13]。已有研究表明农业干旱受气候变化影响较大,但是诸如土地利用变化、水资源开发利用等人类活动的影响也不可忽略。如蒋桂芹[14]分析海河水系1956~1975年和1990~2009年气候变化、土地利用和水资源开发利用对农业干旱的驱动作用,结果分别为40%、4%和-56%。杨志远[15]分析乌裕尔河流域1961~1985年和1986~2011年气候变化和土地利用对农业干旱的影响,发现气候变化的贡献率为15%~62%,土地利用变化的贡献率为38%~85%。黎云云等[16]对比分析黄河流域1968~1990年、1991~2000年和2001~2010年气候变化和土地利用对黄河流域农业干旱的影响贡献率,发现气候变化的贡献率约为50%~90%,土地利用变化的贡献率约为10%~50%。以上贡献率的研究方法中均将单个因素的影响贡献简单相加作为多因素的综合贡献,但对于不同影响因素之间的相互作用考虑不足。对此,刘佳嘉等[17]提出的多因素综合影响贡献量分解方法能改进上述方法的不足。
本文深入研究农业干旱的影响机制,以位于长江中下游地区的抚河流域为例,采用抚河流域二元水循环模型、农业干旱评估法及多因素归因分析法,在动态评价抚河流域长系列农业干旱演变规律的基础上,定量分析气候变化和人类活动对抚河流域农业干旱演变造成的影响。
1 研究区概况及数据来源
1.1 抚河流域概况
抚河流域位于长江中下游地区,隶属于鄱阳湖水系,流域面积为15 767 km2。多年平均降水量为1 755.7 mm,多年平均蒸发量约为1 100 mm,流域内抚州市多年平均水资源总量为160.97亿m3。抚河流域历史旱情是由于降水年内分布极不均匀,且与农田生长需水要求不相协调造成的,以致每年均发生不同程度的旱灾。一般年受旱面积约4.7万hm2(70万亩),以1963年和1978年灾情最为严重。本文以抚河流域大中型灌区作为灌区单元,大中型灌区以外单元作为其他单元,如图1所示。
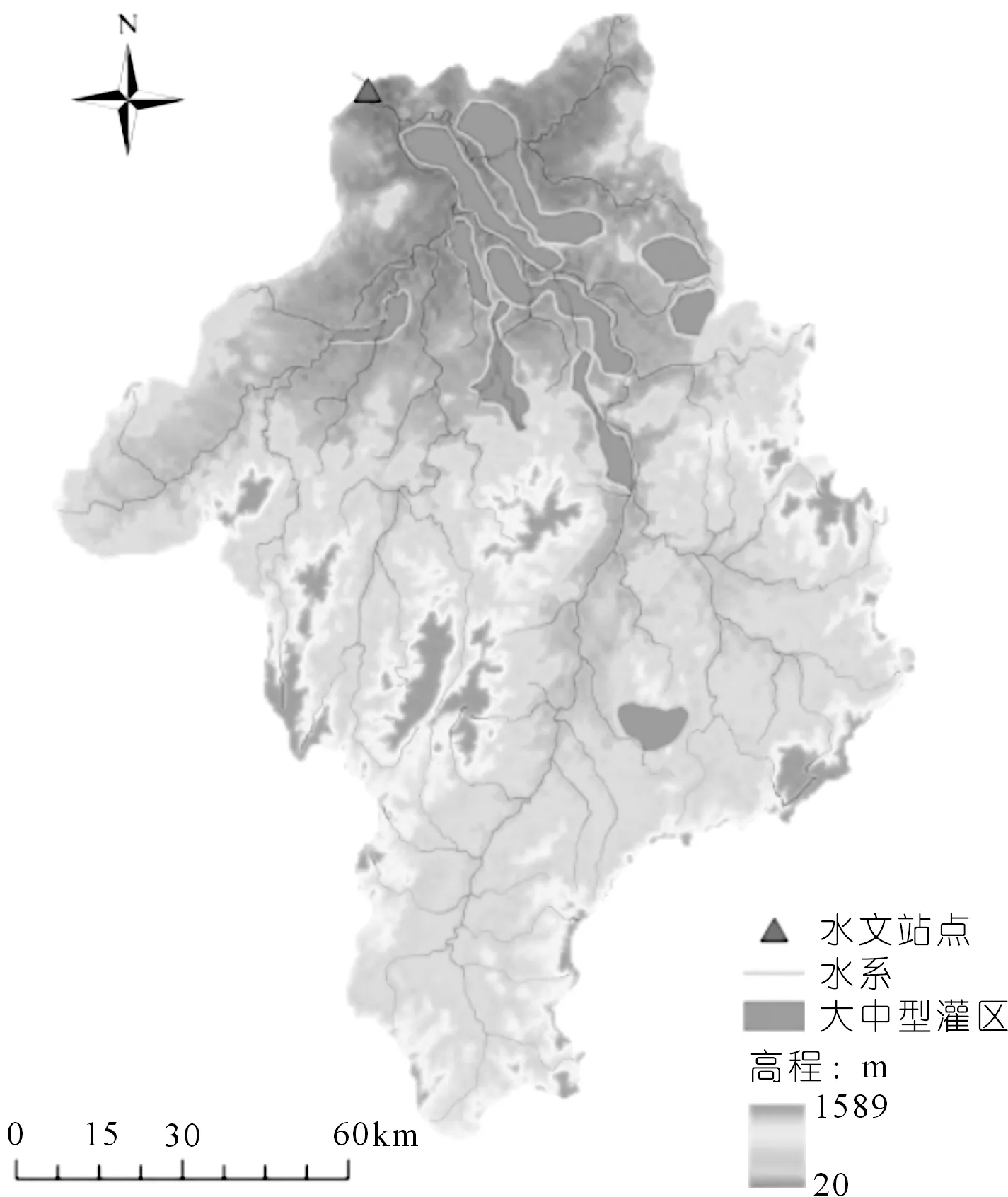
图1 抚河流域研究区概况Fig.1 Overview of the study area in the Fuhe River Basin
1.2 数据来源
本文研究数据包含2类数据:第一类是模型计算需要的数据,主要涉及DEM和河道信息、土地利用类型、土壤类型以及人工取用水数据等数据;第二类是用于模型结果验证的数据,包括李家渡、廖家湾、娄家村等3个水文站逐日流量数据,以及2010~2019年土壤墒情站点数据。
以上各项数据中,1956~2019年3个水文站逐日流量数据来自江西省水文局;1956~2019年2个土壤墒情站点数据来自江西省水文局;11个国家气象站1956~2019年的每日气象数据,包括降水、气温、相对湿度、日照时数和风速,由国家气象信息中心提供;1956~2019年10个雨量站逐日降雨数据来着江西省水文局;DEM数据采用SRTM90,栅格边长为90 m(http:∥srtm.datamirror.csdb.cn/);土地利用数据采用1985年和2015年的LANDSAT TM数据;抚河流域遥感蒸散数据来自MODIS蒸散数据集;土壤数据均采用《中国土种志》上的“统计剖面”资料,采用第二次全国土壤普查结果1∶100 000分辨率的土壤类型图;抚河流域灌区以及大中型水库资料来源于抚州市水资源公报;经济社会用水数据来自抚州市水资源公报和江西省统计年鉴。
2 研究方法
2.1 分布式二元水循环模型
WEP-L分布式二元水循环模型(简称WEP-L模型)是耦合“自然和社会”二元水循环过程的分布式水循环模型[18],目前已在黄河、海河、松花江、汉江、柳江、红河等南北方多个流域进行了应用,本次研究采用WEP-L模型模拟抚河流域农业干旱相关水文要素。
2.1.1模型原理
WEP-L模型[18]的空间计算单元为子流域套等高带,自然水循环过程主要是对各计算单元的降水、入渗、产流、汇流等过程进行模拟,通过下垫面划分和垂向结构对产流过程进行计算,采用“马赛克”法划分土地利用类型,具体为裸地-植被域、灌溉农田、非灌溉农田、水域和不透水域五大类。在垂直方向上,可划分截留层、根系土壤层、过渡层和含水层等。水平方向上,采用一维运动波模型进行汇流过程演算,从上游到下游子流域之间进行河道汇流演算。WEP-L自然水循环过程模拟如图2所示。
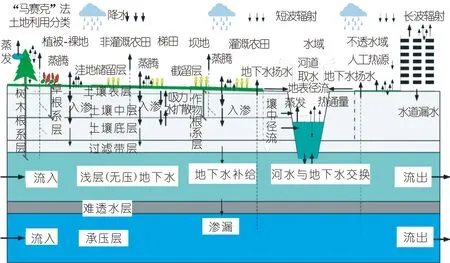
图2 自然水循环模拟Fig.2 Natural water cycle simulation
人工侧支水循环过程[19]集中于取水、输水、储水、用水、排水和耗水6个方面。在大多数情况下,取水和排水是与自然水循环有关的两个关键过程,如图3所示,耦合机制主要发生在这两个过程中。河流、水库和地下水可以被认为是取水来源。取水过程使河流和地下水中的水量减少,排水过程使河流和地下的水量增加。此外,该模型还考虑了废水回用。图4为WEP-L模型耦合的原理。
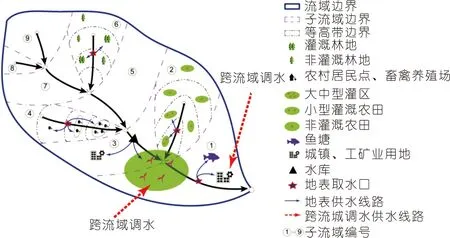
图3 社会水循环模拟Fig.3 Generalizations of social water cycle systems
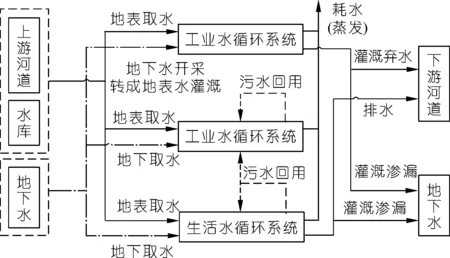
图4 自然、社会水循环耦合原理Fig.4 The coupling principle of natural and social water cycle
2.1.2模型率定验证方法
根据研究对象的突变情况,将研究时间序列划分为基准期和变化期,分别采用水文站月平均流量、土壤墒情站点的月均土壤含水量对抚河流域二元水循环模型进行率定验证,具体计算公式如下:
(1)
(2)
(3)
2.2 干旱演变分析方法
2.2.1农业干旱评价指标
农业干旱通常用土壤含水量来表征,考虑标准化土壤湿度指数计算方法较为常用,所需的长系列土壤含水量数据可通过模拟获得,因此农业干旱选用标准化土壤湿度指数作为评价指标。标准化土壤湿度指数(Standard soil moisture index,SSMI)是一个无量纲的农业干旱指标,通过对土壤湿度指数(Soil moisture index,SMI)标准化得到,SMI的计算公式如下:
(4)
式中:wsim、wwilt和wfc分别为土壤含水量、凋萎系数和田间持水量,其中土壤含水量可通过模型模拟获得。
其次,对土壤湿度指数序列依次进行分布拟合、正态标准化等处理,得到标准化土壤湿度指数(SSMI)。获得某时段的SSMI值的计算公式如下:
(5)
式中:当F≤0.5时,S=-1;当F>0.5时,F=1-F,S=1。其它常数项分别为c0=2.515 517,c1=0.802 853,c2=0.010 328,d1=1.432 788,d2=0.189 269,d3=0.001 308。
2.2.2干旱特征识别方法与评估指标
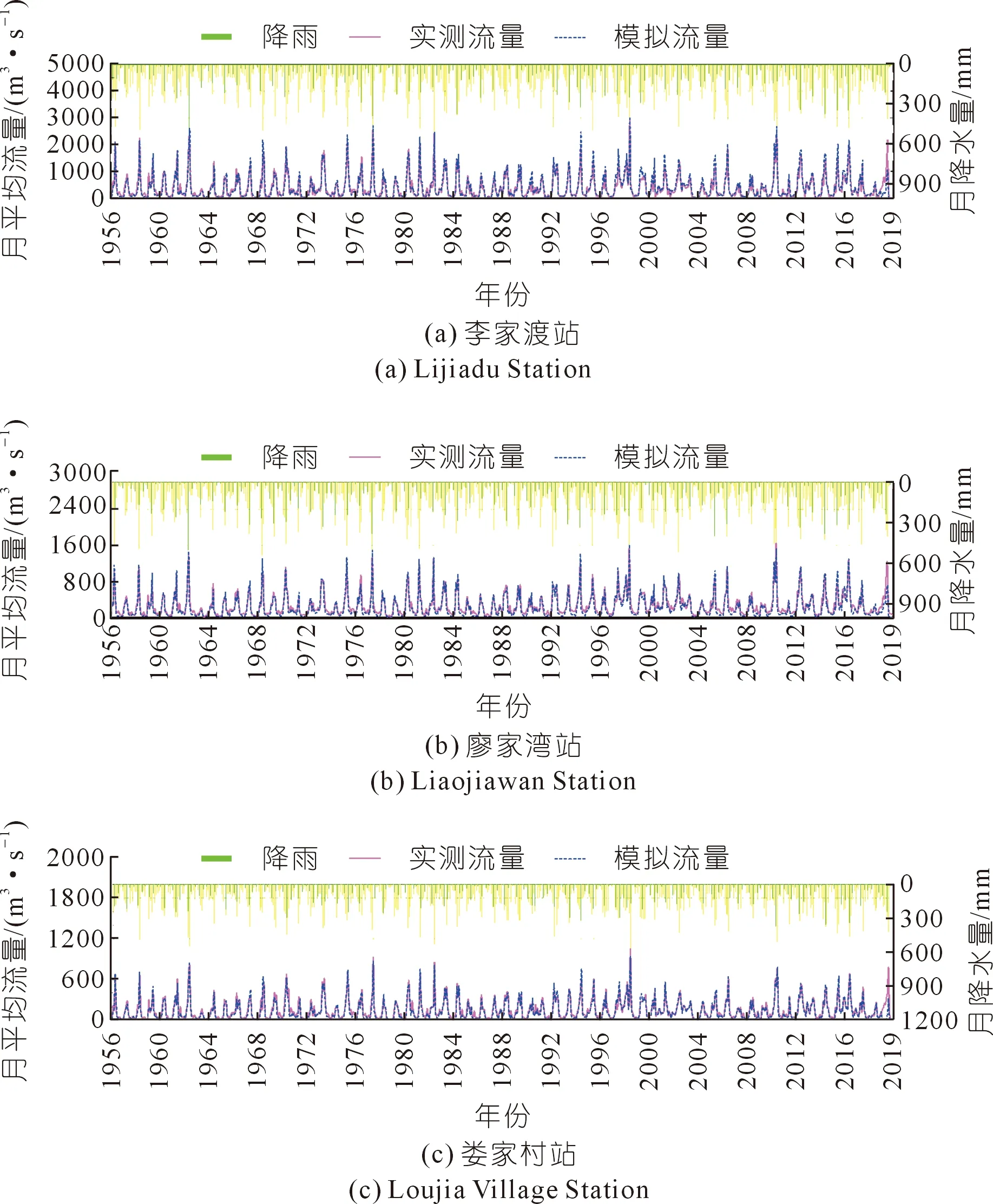
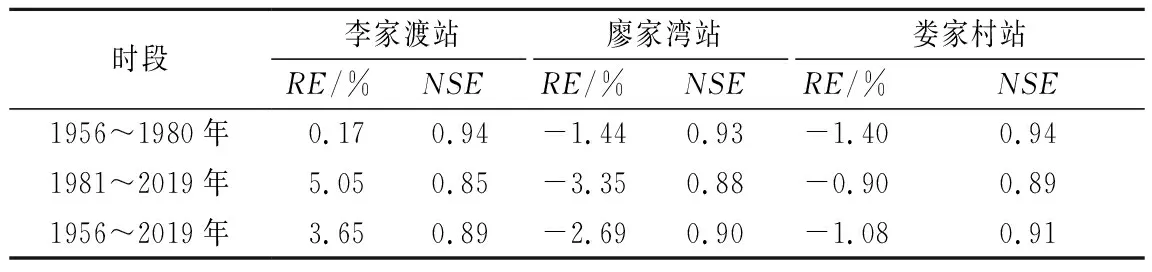
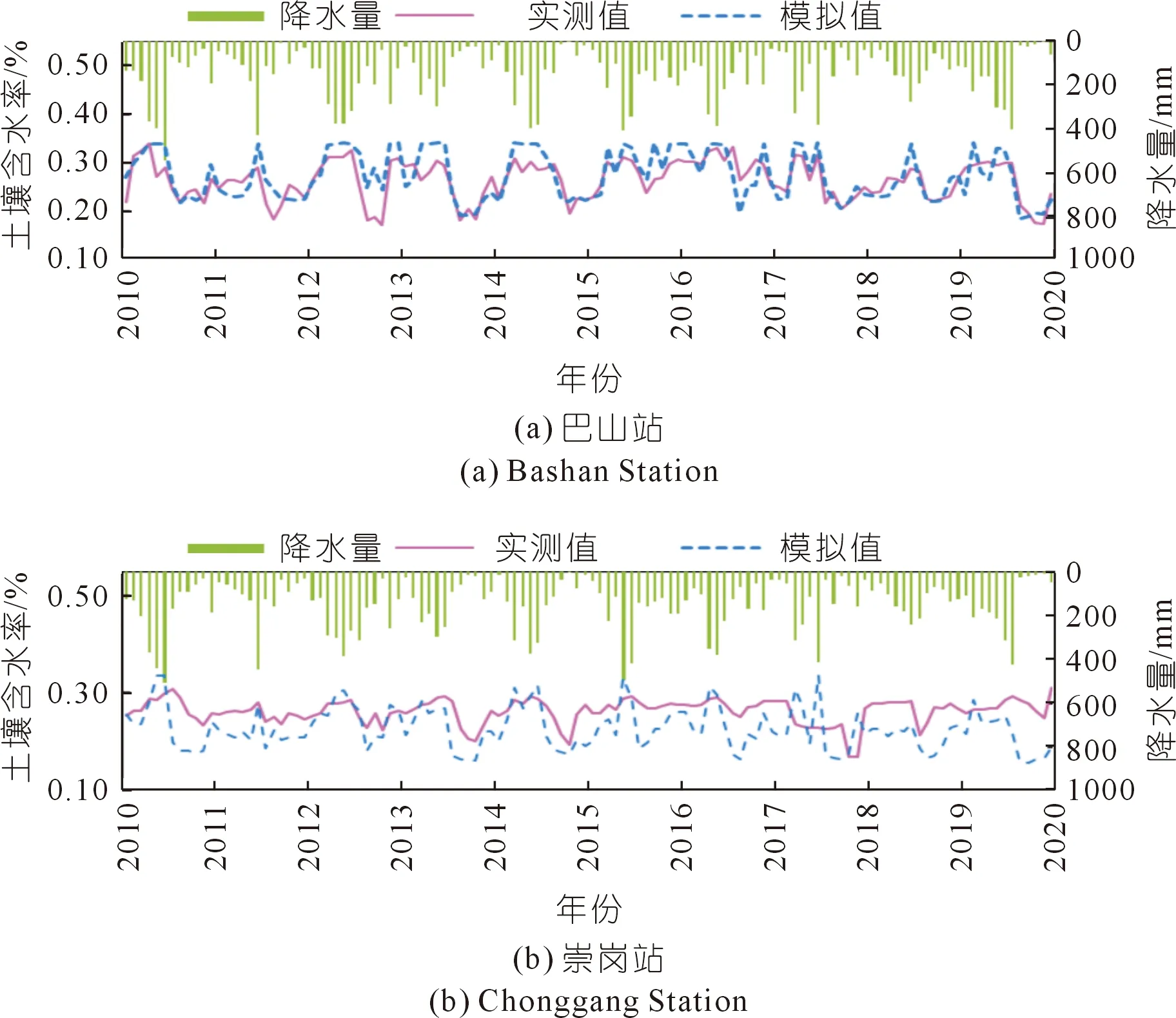
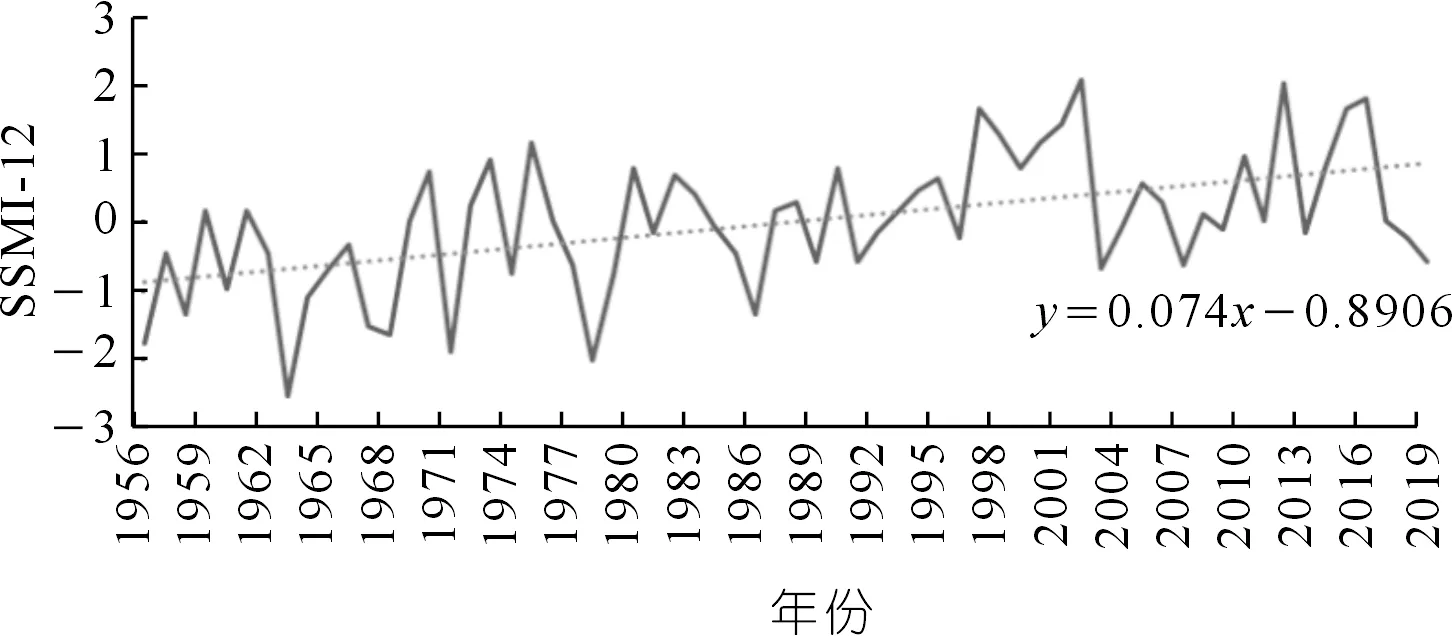
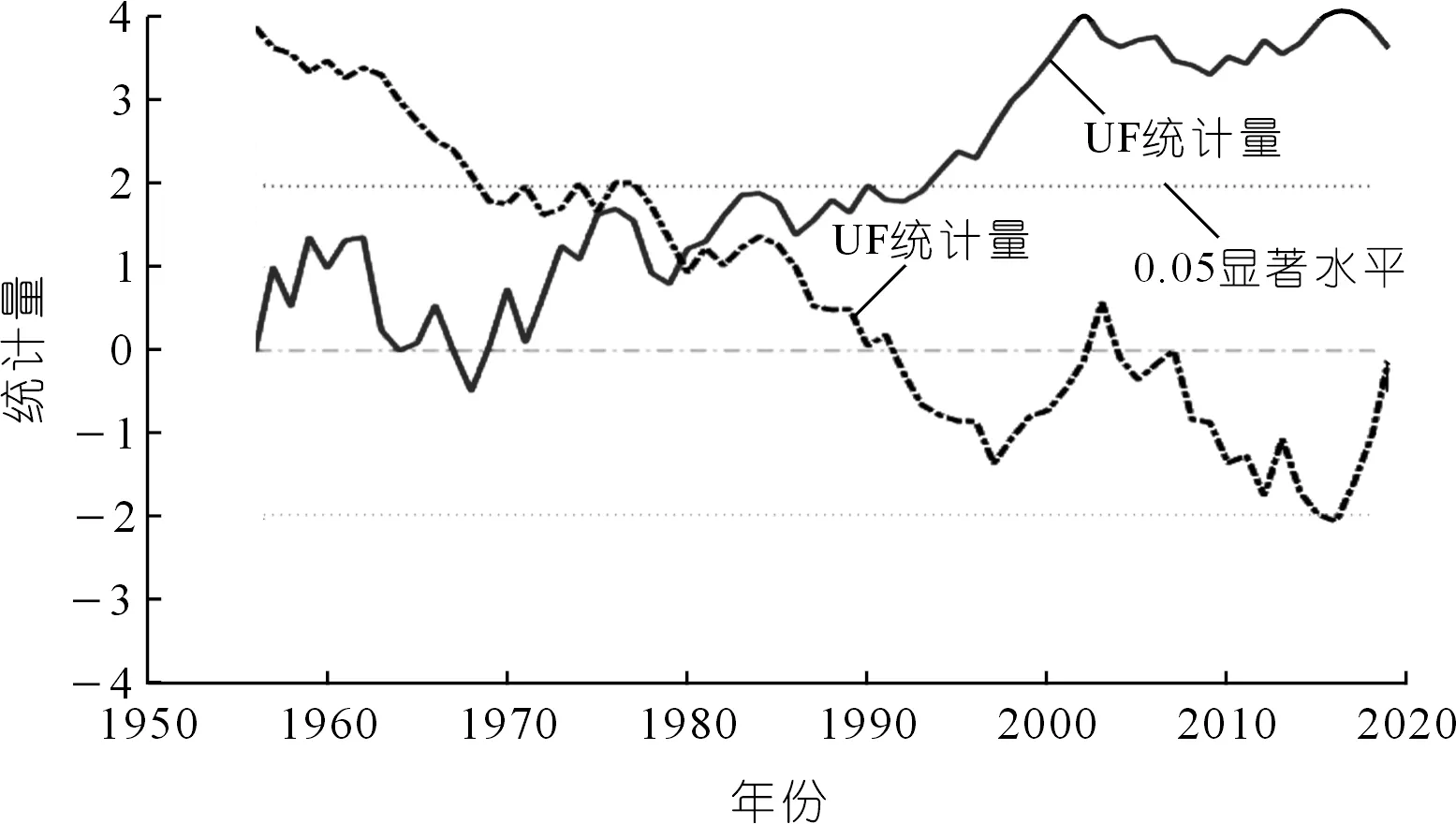
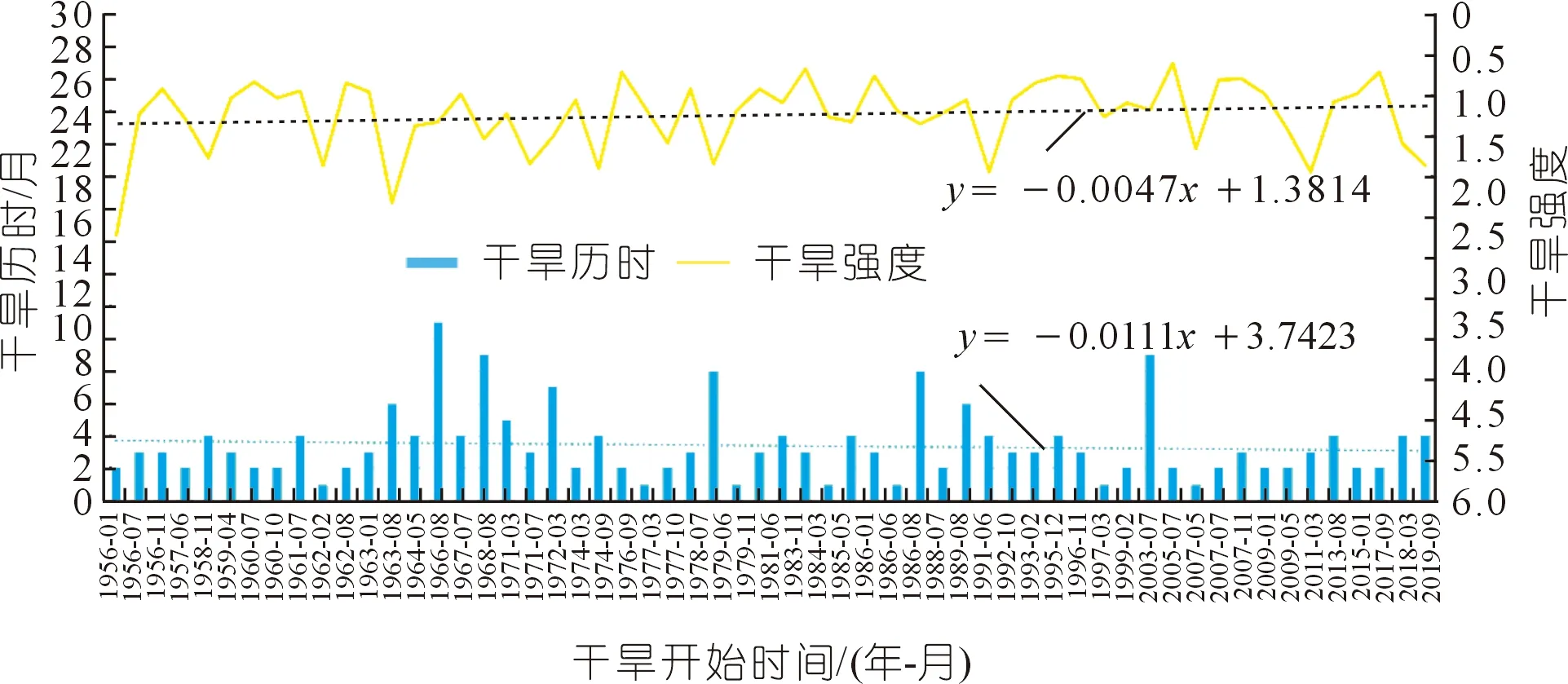
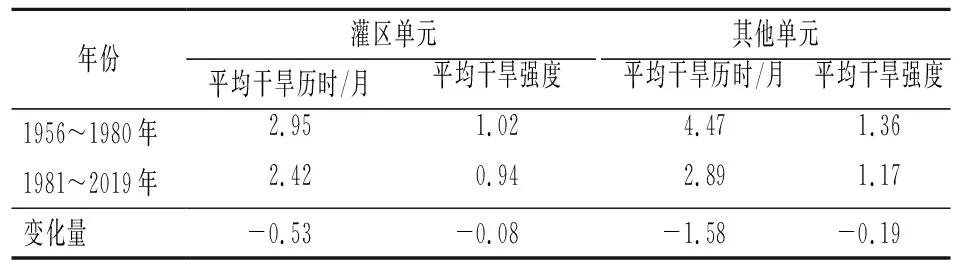
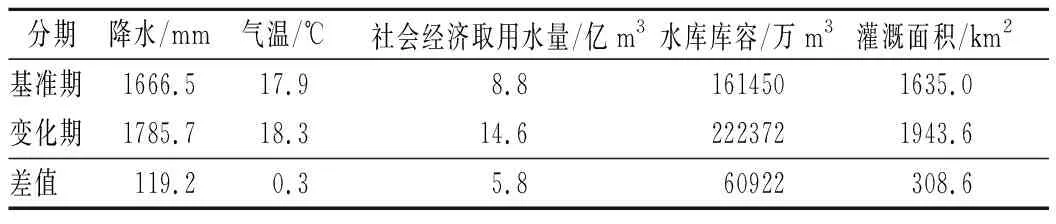
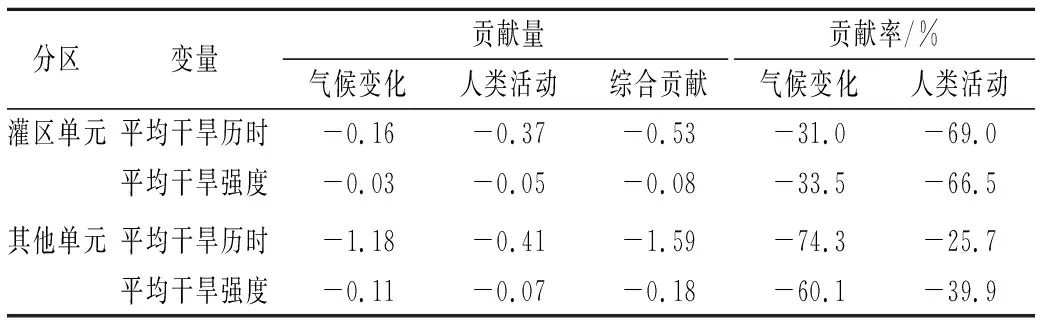
基于干旱评估结果,采用游程理论识别出干旱特征指标,具体包括干旱历时和干旱强度。同时为了尽量减少轻微干旱的影响,研究采用双阈值法对干旱过程进行识别,根据干旱等级评估标准,设定截断水平Z1=-0.5,如图5所示。根据已有长江中下游干旱研究成果[20],设单月干旱事件截断水平Z2=-1.5,间隔期截断水平Z0=0.5,具体过程为:① 将干旱指数视为离散序列,设定截断水平Z1,当干旱指数序列在连续时段出现负游程( 图5 游程理论示意Fig.5 Schematic diagram of run theory 干旱历时(Duration,D)表示基于游程理论识别出的开始和结束时间的时间差;干旱强度(Intensity,I)表示干旱发生时段内干旱指数绝对值之和与时间的比值。 D=j-i+1 (6) (7) 式中,i,j分别表示图5中干旱事件c,d的开始和结束时间;Zi为干旱指数,D为干旱事件的干旱历时。 本文采用多因素归因分析方法对农业干旱演变进行归因分析[17]。根据影响农业干旱的n个因素划分基准气和变化期,然后对不同因素的状态进行交叉组合设置模拟情景,进而采用分布式水文模型模拟得出各情景模拟值,采用公式(4)~(7)计算农业干旱指数及干旱特征,并用于影响贡献量分解计算,贡献量和贡献率分解计算采用以下公式: (8) (9) 式中:ΔXj为第j个因素的贡献量;ai,j为第j个因素对应情景i的权重系数,若该情景下j个因素处于变化期为1,基准期为-1;n为因素个数;γi为第i个因素的占总变化的贡献率。 3.1.1月径流过程率定和验证 根据干旱指数突变的时间,选取李家渡、廖家湾以及娄家村3个水文站1956~1980 年和 1981~2019年逐月流量序列对模型参数进行率定和验证。各站流量过程模拟结果和效率系数如图6和表1所示。率定期3个水文站月径流过程Nash-Sutcliffe效率系数均在0.9以上,相对误差在±2%以内;验证期3个水文站月径流过程Nash-Sutcliffe效率系数均在0.85以上,相对误差在±6%以内。结果表明,WEP-L模型总体上能够较好地描述抚河流域的径流过程。率定期由于人类活动较少,所以相比验证期,率定期模型模拟效果稍好。 图6 1956~2019年抚河流域月流量模拟率定效果Fig.6 Model calibration effect of monthly flow in the Fuhe River Basin from 1956 to 2019 表1 模型率定验证结果Tab.1 Model calibration and validation results 3.1.2土壤含水量率定和验证 基于WEP-L模型模拟了抚河流域等高带单元农田单元根系层的土壤含水量。模型模拟的3层土壤含水量假设在每一层都是均匀分布的,根据各层的深度线性插值成浅层0~10 cm、中层10~20 cm及深层20~40 cm的土壤含水量数据,与实测土壤墒情站点土壤含水量监测深度相对应。由于抚河土壤墒情站点建设较晚,且监测数据连续性不高,因此本文选取时间序列完整的土壤墒情站点巴山站和崇岗站2010~2019年数据,对模型模拟的两个站点的土壤含水率进行验证,结果如图7所示。此外,相关性系数的评价结果表明,两站土壤含水量模拟值和实测值的相关系数分别为0.76和0.40,相对误差均小于5%,表明WEP-L模型模拟的土壤含水量可以较好反映实际土壤含水量的变化过程。 图7 2010~2019年抚河流域月土壤含水率模型率定效果Fig.7 Model calibration effect of monthly soil water content in Fuhe River Basin from 2010 to 2019 3.2.1干旱指数变化规律 采用公式(4)~(5)计算12个月时间尺度的农业干旱指数SSMI(SSMI-12),并对其进行MK趋势检验,发现在90%的置信水平下,抚河流域年尺度SSMI的Z值为3.71,同时结合SSMI-12趋势变化图(图8),可知抚河流域农业干旱在年尺度上呈现显著湿润化趋势。采用MK突变检验法对年尺度的SSMI进行突变检验,结果如图9所示。选取0.05显著性水平的置信区间(±1.96)作为临界曲线的MK检验值,根据突变检验结果,发现抚河流域农业干旱年尺度存在突变性,突变开始时间是1980年。 图8 抚河流域1956~2019年SSMI趋势变化Fig.8 SSMI changes in the Fuhe River Basin from 1956 to 2019 图9 抚河流域1956~2019年SSMI突变诊断Fig.9 SSMI mutation diagnosis for the Fuhe River Basin from 1956 to 2019 3.2.2干旱特征变量变化规律 根据干旱特征识别方法中的游程理论识别出1956~2019年抚河流域发生农业干旱的次数,通过公式(6)~(7)计算得到各次农业干旱的历时和强度,如图10所示。由图可知,抚河流域1956~2019年发生农业干旱事件共计58次,总体上,干旱历时和干旱强度呈现减少的趋势。由表2可知,相比1980之前,1980年以后灌区单元平均干旱历时减少0.53个月,平均干旱强度减少0.08。其他单元平均干旱历时减少1.58个月,平均干旱强度减少0.19。 图10 1956~2019年抚河流域农业干旱历时和干旱强度统计Fig.10 Statistics on duration and intensity of agricultural drought in the Fuhe River Basin from 1956 to 2019 表2 基准期和变化期农业干旱特征变量变化Tab.2 Changes of agricultural drought characteristic variables in base period and change period 3.3.1多因素归因情景方案 根据农业干旱指数的突变性分析结果,确定抚河流域农业干旱演变影响机制分析的基准期和变化期分别为1956~1980年和1981~2019年。情景设置如表3所列。由于主要考虑气候变化(主要涉及降水、气温)和人类活动(主要涉及社会经济取用水量、水库库容和灌溉面积)2类因素,因此共设置4个情景。基准期与变化期不同因素的设置见表4。不同时期代表气候变化和人类活动的5个指标的多年平均值如表5所列。由表可知,相比于基准期,变化期的降水年均值增加119 mm,气温年均值增加0.3 ℃,社会经济取用水量年均值增加5.8亿m3,水库库容均增加60 922万m3以及灌溉面积增加308.6 km2。 表3 抚河流域农业干旱影响机制分析的情景方案设置Tab.3 Scenario settings for analysis of impact mechanism of agricultural drought in the Fuhe River Basin 表4 基准期和变化期不同因素的设置Tab.4 Setting of different factors in base period and change period 表5 抚河流域农业干旱相关主要影响因素特征值Tab.5 Characteristic values of main influencing factors related to agricultural drought in the Fuhe River Basin 3.3.2农业干旱影响机制分析 采用WEP-L模型对各情景分别进行模拟,根据模型模拟结果,采用公式(6)~(7)计算干旱特征变量,采用公式(8)和(9)计算气候条件和人类活动两个因素对干旱贡献率,如表6所列。从表6可以看出: 表6 气候变化和人类活动对农业干旱的影响Tab.6 Impacts of climate change and human activities on agricultural drought (1) 从各要素对农业干旱历时的影响来看,气候变化和人类活动都起到减缓作用。对灌区单元内的农业干旱而言,人类活动影响最大,贡献率为-69.0%;其次是气候变化,贡献率为-31.0%。对其他单元内的农业干旱,气候变化影响最大,贡献率为-74.3%;其次是人类活动,贡献率为-25.7%。 (2) 从各要素对农业干旱强度的影响来看,气候变化和人类活动都起到减缓作用。对灌区单元内的农业干旱而言,人类活动影响最大,贡献率为-66.5%;其次是气候变化,贡献率为-33.5%。对其他单元内的农业干旱,气候变化影响最大,贡献率为-60.1%;其次是人类活动,贡献率为-39.9%。 以上针对农业干旱演变的归因分析中,气候变化和人类活动都起到减缓作用,且对于灌区单元而言,社会经济取用水、水库和灌溉等人类活动的贡献率高于气候变化,而其他单元人类活动的贡献率低于气候变化。结合基准期和变化期各项指标的变化情况,可以得出,降水作为导致干旱发生的关键因素,其年均值变化期高于基准期,因此导致气候变化在农业干旱演变过程中起到减缓的作用。相应地,在表征人类活动的各项指标中,水库库容增加能一定程度增大干旱发生时期的用水量,同时取用水量和灌溉面积的增加能弥补作物关键生育期土壤水分的不足,保证作物的正常发育,这在一定程度上能达到缓解农业干旱的目的。 本文以抚河流域作为研究对象,基于二元水循环模型的干旱评估方法,并采用多因素归因分析法对气候变化和人类活动对农业干旱的贡献进行分析,对推动水文水资源学科与干旱灾害研究融合具有重要意义。 (1) 通过构建的抚河流域基础数据平台,搭建了抚河流域分布式水循环模型。模拟结果表明,径流模拟的NSE均大于0.85,相对误差小于±5%。两个墒情监测站土壤含水量模拟值和实测值的相关系数分别为0.76和0.40,相对误差均小于5%,模型模拟效果符合要求。 (2) 抚河流域年尺度SSMI呈现增加趋势,流域农业干旱存在突变性,农业干旱的突变点在1980年。 (3) 气候变化和人类活动要素对抚河流域农业干旱的平均干旱历时和平均干旱强度均起到减缓作用。气候变化和人类活动对灌区单元平均干旱历时的贡献率分别为-31%和-69%,对平均干旱强度的贡献率分别为-33.5%和-66.5%。气候变化和人类活动对其他单元平均干旱历时的贡献率分别为-74.3%和-25.7%,对平均干旱强度的贡献率分别为-60.1%和-39.9%。由于数据时段的限制,下一步将考虑2022年长江流域特大干旱的数据,开展进一步研究。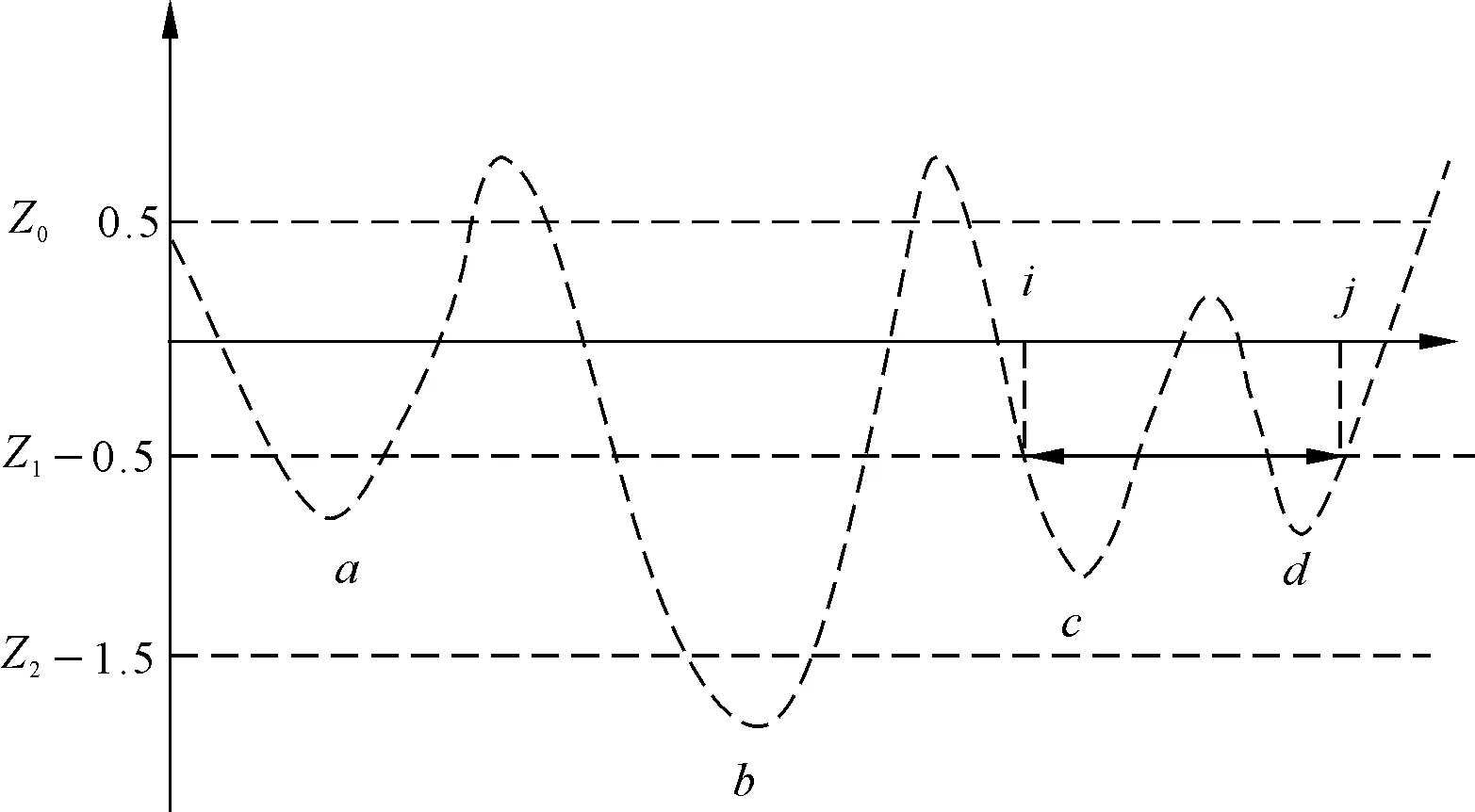
2.3 多因素归因分析方法
3 结果分析
3.1 抚河流域分布式二元水循环模型验证
3.2 抚河流域农业干旱演变规律
3.3 抚河流域干旱演变影响机制分析


4 结 论
