嵌入式系统中激活函数的快速计算

梁 东，杨 涛，曹鑫磊，吕建良

（中国航天空气动力技术研究院，北京 100074）

0 引 言

在多层神经网络系统中，上层节点的输出与下层节点的输入之间具有一个函数关系，这个函数被称为激活函数。为了提高神经网络的适应性，在神经网络计算中，必须引入非线性函数作为激活函数[1-3]，常用的激活函数包括Sigmoid函数[4]、Tanh函数和ReLU函数等。

随着神经网络算法的应用普及，在嵌入式系统中进行神经网络计算的情况越来越多，虽然部分嵌入式处理器中增加了硬件乘法器，但多数嵌入式系统的性能较电脑仍有较大差距，且复杂非线性的激活函数计算耗时严重，因此提高神经网络中激活函数的运算速度对于确保神经网络的实时性具有重要意义。

1 激活函数分析

常用的激活函数Sigmoid见式（1）：

Sigmoid函数输出波形如图1所示，其输出范围为0～1，一般用于预测概率作为输出模型，但其输出为非0均值，会降低权重更新的效率，同时幂函数运算求解复杂，降低了系统实时性。

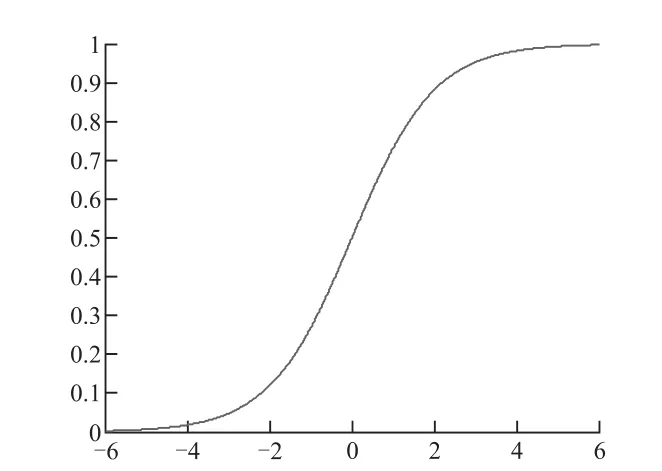
图1 Sigmoid函数波形

Tanh函数如下所示：

Tanh函数输出波形如图2所示，其解决了Sigmoid函数非零均值的问题，因此其应用最为广泛，但其仍存在梯度消失和幂函数运算的问题。在嵌入系统中应用时可简化为式（3），以减少幂函数的运算。

图2 Tanh函数波形

ReLU是分段性函数，如式（4）所示，计算其实时性可以满足使用要求，但其非线性较弱，因此，一般用于多层神经网络系统中。

综上所述，Sigmoid函数和Tanh函数均存在幂运算复杂，降低了神经网络实时性的问题，进而限制了神经网络运算在嵌入式系统中的应用。本文以ex为例，实现幂函数的快速计算。

2 快速计算原理

2.1 存储格式

在嵌入式系统中，浮点数采用IEEE754格式存储[5-7]，以单精度浮点数格式为例，IEEE单精度浮点数格式共32位，包含3个构成字段，1位符号s，8位偏置指数e，偏置值为127，23位尾数f，如图3所示。浮点数真值F见式（5）。

图3 单精度浮点数存储格式

以103.5为例，首先将十进制转化为二进制数，见式（6）：

将式（6）进行规格化则有：

根据单精度浮点数的存储格式则有：

因此，浮点数103.5在嵌入式系统中存储的十六进制代码为：42CF0000h。

2.2 计算原理

激活函数中常见的幂函数见式（11）：

首先，根据函数特点及浮点数的存储格式可知，y=ex＞0，因为浮点数y的符号位s=0。为与嵌入系统中单精度浮点数的存储格式对应，对式（11）两边同时取2的对数则有：

进而可得：

式中：n=[xlog2e]是xlog2e的整数部分，须满足n≤[xlog2e]；E为xlog2e的小数部分，E=xlog2e-n，须满足0≤E≤1。

对比式（5）和式（13）可知，y的偏置指数为：

尾数见式（15）：

由于0≤E≤1，因此可直接利用2x在0处的泰勒展开公式进行估算[8]。为进一步降低泰勒展开公式的复杂度，对式（15）进行变换，换成ex的格式，见式（16）：

由0≤E≤1可知，0≤Eln2≤0.693 2，因此可利用式（17）进行估算：

式中，x=Eln2，计算出尾数f后，右移23位，即可写入浮点数的尾数中。至此，y的符号位、偏置指数位、小数位均计算完成，y=ex计算完毕。

3 算法实现

利用C语言实现上述算法，流程如图4所示。在计算中需考虑输出结果是否在单精度浮点数的数据范围内。

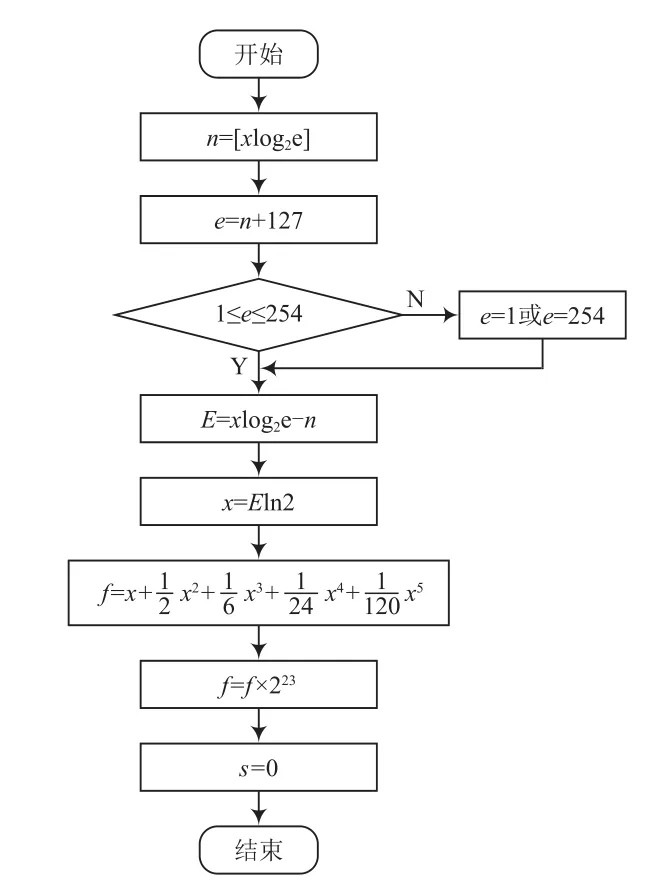
图4 函数实现流程

4 试验验证

在STM32F427上进行试验验证，其主频为180 MHz，具有FPU（浮点运算器）单元[9-10]，首先进行精度验证，为满足输出结果为单浮点精度数，x取[-87：1：88]，分别采用本文的方法（fast_exp）与math函数库中的exp（）函数进行计算，按式（18）进行误差计算：

相对误差范围量级在10-6，可以满足一般神经网络的计算需求，若需进一步提高精度，将式（17）的高阶泰勒展开项加入计算中即可。

为检验运算速度，分别采用本文的方法与exp（）函数计算10 000次，以随机数x=12.543 36为例，试验结果显示，采用本文的方法耗时217.5 ms，采用exp（）函数计算耗时4 158.8 ms，计算时间减少了94.77%，大大提高了幂函数运算的实时性。

5 结 语

本文总结了神经网络系统中常用的激活函数，并对激活函数中幂函数的快速计算方法开展研究，利用嵌入式系统浮点数的存储格式及泰勒级数展开，实现了幂函数的快速计算，在嵌入式系统中验证后可知，计算精度达10-6以上，计算时间减少了94.77%，大大提高了幂函数的运算速度，对于提高神经网络算法在嵌入式系统中应用的实时性具有重要意义。