Quasi-static magnetic compression of fieldreversed configuration plasma: amended scalings and limits from two-dimensional MHD equilibrium

Abba Alhaji BALA,Ping ZHU (朱平),Haolong LI (李浩龙),Yonghua DING (丁永华),Jiaxing LIU (刘家兴),Sui WAN (万遂),Ying HE (何莹),Da LI (李达),Nengchao WANG (王能超),Bo RAO (饶波) and Zhijiang WANG (王之江)

1 International Joint Research Laboratory of Magnetic Confinement Fusion and Plasma Physics,State Key Laboratory of Advanced Electromagnetic Engineering and Technology,School of Electrical and Electronic Engineering,Huazhong University of Science and Technology,Wuhan 430074,People’s Republic of China

2 School of Physics,Huazhong University of Science and Technology,Wuhan 430074,People’s Republic of China

3 Department of Physics,Federal University Dutse,Jigawa 720101,Nigeria

4 Department of Engineering Physics,University of Wisconsin-Madison,Madison,Wisconsin WI-53706,United States of America

5 College of Physics and Optoelectronic Engineering,Shenzhen University,Shenzhen 518060,People’s Republic of China

Abstract In this work,several key scaling laws of the quasi-static magnetic compression of field reversed configuration (FRC) plasma (Spencer et al 1983 Phys.Fluids 26 1564) are amended from a series of two-dimensional FRC MHD equilibriums numerically obtained using the Grad-Shafranov equation solver NIMEQ.Based on the new scaling for the elongation and the magnetic fields at the separatrix and the wall,the empirically stable limits for the compression ratio,the fusion gain,and the neutron yield are evaluated,which may serve as a more accurate estimate for the upper ceiling of performance from the magnetic compression of FRC plasma as a potential fusion energy as well as neutron source devices.

Keywords: magneto-hydrodynamic equilibrium,Grad-Shafranov equation,field reversed configuration,NIMEQ,magnetic compression

1.Introduction

Field-reversed configuration (FRC) is an elongated compact torus plasma sustained solely by a poloidal magnetic field[1].Because the FRC has no or little toroidal magnetic field,it has a very high plasma beta (〈β〉 averaged over the separatrix volume lies in the range of 0.5-1).The magnetic field of FRC is composed of open magnetic field lines,separatrix,and closed magnetic field lines,while the plasma almost entirely exists inside the separatrix with an attractive feature of having no material objects linking the torus.The two FRC regions are referred to as ‘open’ and ‘closed’ respectively [2].

FRC has been one of the preferred candidate configurations for fusion devices such as compact nuclear fusion reactors and neutron sources,which has received increasing attentions from various countries.Both experimental and theoretical studies have been performed to explore the potentials and challenges associated with such an attractive path towards fusion [3-6].The C-2 experiment in TAE Technology has been able to obtain and maintain an FRC withnreaching3 × 1019m-3,TeandTiaround 1 keV respectively,the energy confinement timeEτabout 1 ms,and theβaround 90 percent [7].The Los Alamos National Laboratory (LANL) and the ALPHA project in the United States successfully increased the temperature and density of an FRC plasma by 1 order of magnitude using staged magnetic compression [6].Japan,Canada,Russia and other countries also have related experimental devices as well [8].In China,the Huazhong field reversed configuration has been designed to explore a novel concept of‘two-staged’magnetic compression of FRC as a path to achieve a compact and economic neutron source and potential fusion reactor [9].

Magnetic compression of FRC is one of the promising paths to fusion that has been pursued over years.For instance,the Princeton ATC device [10]has increased the plasma density by 5 times with adiabatic compression.The FRX-C/LSM device of LANL also adopted the adiabatic compression method for FRC,and the plasma temperature and density are increased by 10 times and 5 times respectively [11].

A one-dimensional (1D) model for the adiabatic compression of FRC [12,13]was established.In this theory,the quasi-static approximation is used such that compression process is considered as a series of MHD equilibria with sequentially varying compression ratio.Although the magnetic compression of FRC plasma is a highly nonlinear 3D dynamic process,the quasi-static approximation allows us to establish the scaling laws and to evaluate the upper stable limits achievable for the compression ratio,fusion gain and neutron yields from such an approach.

However,1D approximations are often made in order to obtain the analytical scaling laws for compression,where the two-dimensional (2D) MHD equilibrium conditions or constraints on the FRC parameters are often not well satisfied.The FRC equilibrium is essentially two-dimensional,and previous theory models for FRC magnetic compression often fail to take into account the 2D spatial and geometric features of FRC equilibrium.More importantly,previous FRC magnetic compression theories have not considered the constraints imposed on the accessible parameter space due to the macroscopic instabilities of FRC plasmas.Therefore,subject to the constraints from the strict FRC 2D equilibrium and the stability criterion,whether the FRC plasma parameters can achieve the fusion ignition conditions through the approach of magnetic compression remains one of the primary problems to address in the design of FRC neutron source and fusion reactor today.

In order to explore this major issue,in this work,we use a series of 2D FRC MHD equilibria from numerically solutions of the Grad-Shafranov (G-S) equation to obtain the amended scaling laws for the key parameters of the FRC plasma during quasi-static magnetic compression including 2D spatial geometric effects,and together with empirical criterion for FRC kinetic MHD stability,to evaluate the fusion ignition conditions and the upper limit of neutron yield that can be achieved through the stable FRC magnetic compression process in the resistive MHD model.

Figure 1.(a)The numerical error En ofψ as a function of the element polynomial degree for 2 × 2 element mesh () and 8 × 8element mesh () in FRC equilibrium.(b) The numerical error En ofψ as a function of the number of elements for the 2nd order elements ()and the 4th order elements().The black lines stand for the scaling fitted from the decaying numerical errors,where N denotes thenumber of elements.

The rest of this work is organized as follows.In section 2,the numerical FRC equilibrium solution is determined and checked for convergence.In section 3,the 2D MHD equilibriums during a quasi-static FRC compression process are solved and the numerical solutions are used to obtain the amended scalings for compression.In section 4,the empirically stable limits for the compression ratio,the fusion gain,and the neutron yield are evaluated.Finally,summary and discussion are given in section 5.

2.The FRC equilibrium

Figure 2.Contours of equilibrium magnetic flux functions ψ (R ,Z)with initial elongation κ 0= 1and maximum pressure μ 0 Pm i=0.0018,for various radial compression ratios .σ The black dash line denotes the separatrix.The units of R and Z are m.

In this work,we solve for the 2D MHD equilibrium of FRC that are consistent with the analytical scaling law for the maximum pressure in radial profile during the magnetic compression based on a 1D approximation.The 2D MHD equilibrium of FRC can be obtained from solving the G-S equation.Besides the limited analytical G-S solutions of FRC equilibria[14-17],numerical methods have been applied to solving the G-S equation using 2D spectral element [18],method of fundamental solutions,finite difference method,boundary element method,conformal mapping and Green’s function.Correspondingly,numerical toroidal equilibrium codes have been developed,such as EFIT,CHEASE,ESC,and NIMEQ[15].In this study,we use the G-S equilibrium solver NIMEQ which is based on the spectral element expansions in two dimensions.The NIMEQ solutions for the 2D FRC equilibriums with different compression ratios are then used to obtain the compression scaling laws,which are compared with the Spencer theory based on 1D approximation.

From the force balance equation,the magnetic divergence constraint,and Ampere’s law,we obtain the G-S equation for the MHD equilibria of an axisymmetric toroidal system.The FRC is characterized by a zero toroidal field,thus the G-S equation for the FRC equilibrium takes the form as

wheretψis the flux inside the separatrix,P0andP2are constants,equation (1) is reduced to the following linear equation forψ

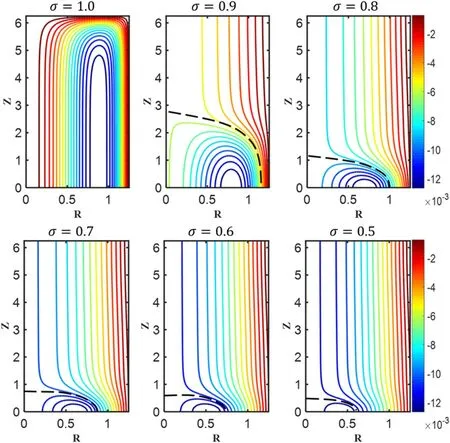
Figure 3.Contours of equilibrium magnetic flux functions ψ (R ,Z)with initial elongation κ 0= 5and maximum pressure μ 0 Pm i=0.0018,for various radial compression ratios σ .The black dash line denotes the separatrix.The units of R and Z are m.

We look for solutions in the cylindrical coordinatesRandZthat are symmetric with respect to the middle planeZ= 0.With boundary conditionsψ(R,Z)= 0atR=aandZ= ±b,whereh= 2b,andaandhare the radius and the length of the cylinder containing the FRC plasma respectively,we obtain

For a more general pressure profileP(ψ) ,we numerically solve the G-S equation (1) using the NIMEQ code,which is a G-S equilibrium solver developed within the framework of NIMROD for the more realistic geometry [18].The finite element method is used to solve the G-S equation and the Picard scheme is used to advance the iteration.To demonstrate the numerical accuracy and convergence of the NIMEQ code,the numerical and analytical solutions of equation (1) are compared for the special case of pressure profile in equation(2)in terms of the numerical error defined by

whereψNis the numerical solution from NIMEQ andψAis the analytic solution from equation (4),and the summation is performed over all of the finite-element nodes.

Two methods are applied to examine the convergence of the NIMEQ solution,namely,the h-refinement and p-refinement.In the p-refinement method,the polynomial degree is increased as the number of elements is kept constant.In contrast,in the h-refinement method,the polynomial degree is fixed while the number of elements is varied.Both methods of comparisons show numerical convergence of the NIMEQ solutions (figure 1).

3.FRC equilibrium during quasi-static magnetic compression

The pressure profile inside the separatrix of an FRC plasma during compression can be modelled as

For any specific radial compression ratio,the 2D FRC equilibrium equation(8)is numerically solved using NIMEQ.The external coils are applied to ensure that the NIMEQ radial compression ratioRs/RwatZ= 0matches that of the pressure profile (figures 2 and 3).For both small and large initial elongations,the last closed flux surface as well as the separatrix of FRC shrinks quickly along the axial direction(i.e.Z-direction) as the FRC is compressed radially to each value ofσ.The FRC lengthlscan be measured from the intersection between the separatrix and theZ-axis atR=0,the elongationκ=ls/2Rs,and the magnetic field at the wallBware compared between the measured values from the 2D MHD equilibrium solutions and the following Spencer scaling law (equations (9)-(11)) for various radial compression ratios (figure 4)

whereRs0=Rw,and the magnetic field magnitudeBwat wall is measured from the equilibrium solution at(Rw,0) .

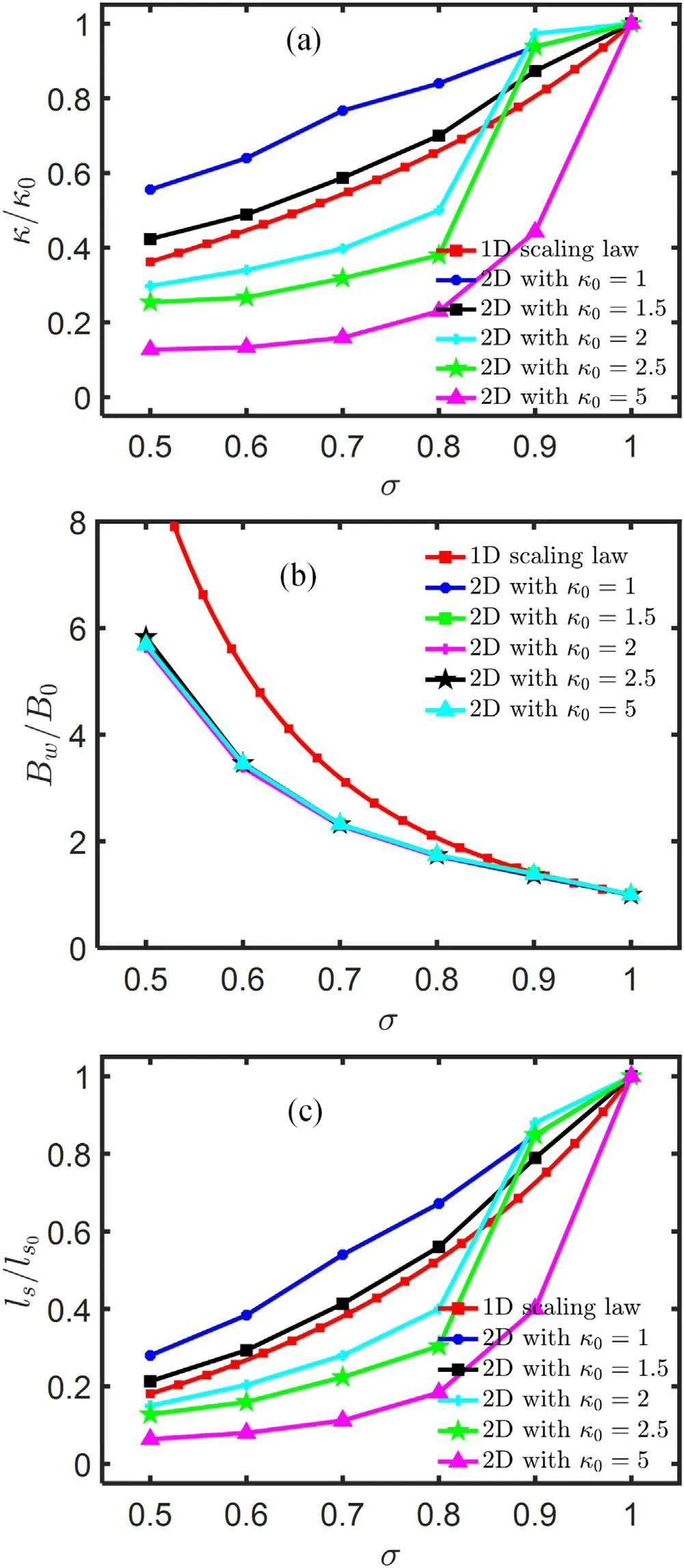
Figure 4.(a) Elongation κ ,(b) wall magnetic field B w ,and (c) FRC separatrix length ls as functions of the radial compression ratioσ from 1D scaling law and 2D MHD equilibrium with various initial elongations.Here the initial separatrix length l s0 = 2.5 m,3.75 m,5.0 m,6.25 m,and 12.5 m for various initial elongations κ0 respectively,and the initial magnetic field strength at wall B0 = 0.06 T which is same in all other figures.

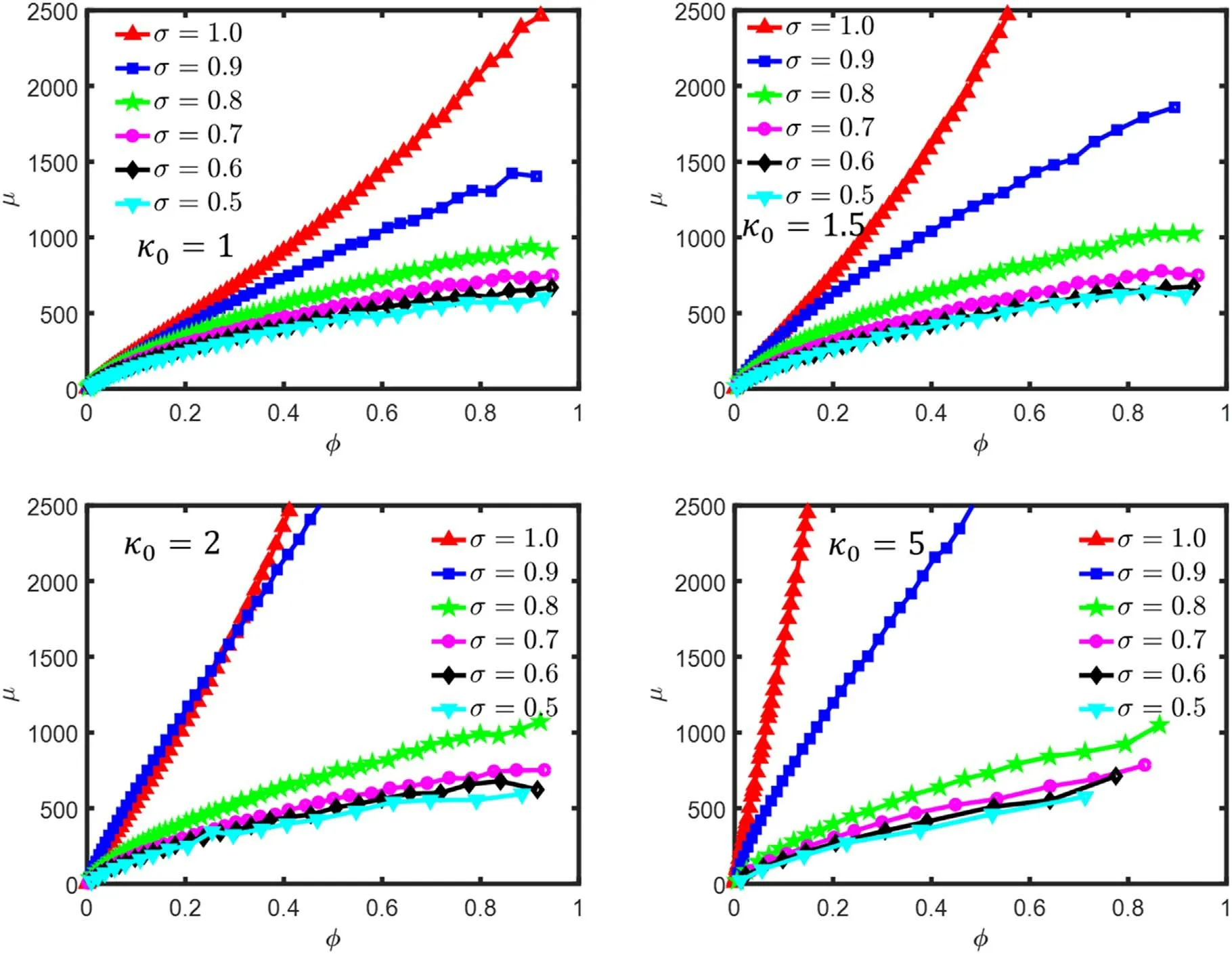
Figure 5.The μ (ϕ )profiles evaluated from 2D MHD equilibrium with various initial elongations for μ 0 Pm i=0.0018.

Where as the comparisons show overall quantitative agreement,the degree of quantitative agreement depends on the FRC equilibrium elongation,which is defined as the ratio of the FRC lengthlsover radiusRsat separatrix for the initial elongationκ0= 1.5,the agreement on thelsandκscalings are the best for the smaller initial elongation,the FRC shape measured from 2D equilibrium shrinks slower than the 1D Spencer scaling law.As the initial elongation increases,the shrinking of FRC during compression becomes faster from 2D equilibrium calculations than 1D Spencer scaling law,as indicated in figures 4(a) and (c).This finding may appear surprising,since the Spencer scaling law is expected to apply best when FRC is highly elongated and hence the 1D approximation is more valid.However,the 2D equilibrium calculations show that,even for the FRC with large initial elongation (e.g.κ0≥5),once the magnetic compression process begins,the FRC elongation itself quickly drops out of the regime where the 1D approximation is valid.

For the entropy per unit flux

its 1D approximation for the elongated FRC is based on[12]

where l(ψ) is the half circumference of the flux surface labelled withψin the poloidal plane,and may be approximated aslsin the 1D model for the elongated FRC.Comparisons of the μ(ψ) profiles calculated from the 2D MHD equilibrium using equation (12) with various initial elongations and radial compression ratios(figure 5)suggest that the adiabatic condition underlying the Spencer scaling law is less satisfied in the quasi-static magnetic compression process modelled by the series of 2D MHD equilibriums.This may also contribute to the differences between compression scalings measured from the 2D equilibrium and calculated from the 1D Spencer scaling laws.

4.Stable limits of FRC compression

4.1.FRC stability criterion

Based on experimental data,an empirical stability criterion of FRC can be written as [19-21]

Using the analytical scaling law for the adiabatic compression of an elongated FRC [12]

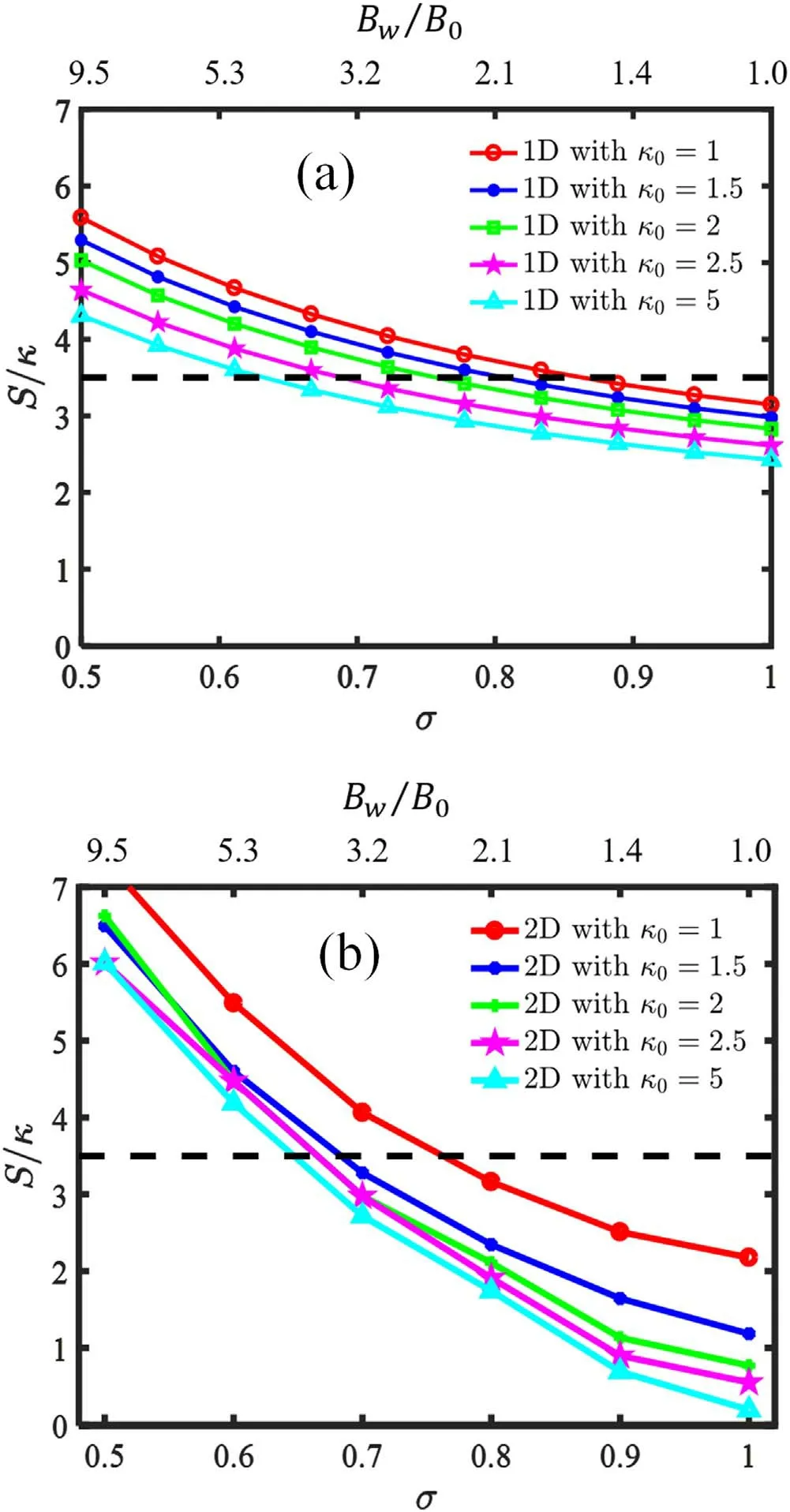
Figure 6. The S /κ stability criterion calculated from (a) 1D scaling laws and (b) 2D MHD equilibrium for different radial compression ratiosσ and magnetic field strengths at the wall B w,with various initial elongations, n i0 =3.0 × 101 9 m -3 ,γ =5/ 3,and ϵ = -1/ 4.

wherels0andni0are the scale length of the separatrix and number density for the initial equilibrium,respectively,we obtain an estimate of the ratio /S κfor a given radial compression ratioσas

The FRC compression results in a reduction in the separatrix radiusRs,but also an even more rapid reduction in the separatrix elongationκ.As a consequence,the more the FRC is compressed,the faster it reaches the stability boundaryS/κ＜ 3.5and goes unstable,as indicated in fgiure 6.Moreover,the figure further indicates that when the initial elongation increases,the stability window of the compression process becomes broader.The stability boundary crossing range ofσreduces from ～[0.63,0.88]in the 1D model to ～[0.65,0.77]in the 2D results.The fact that the stability boundary crossing values ofσmostly differs for the small initial elongation cases,suggests the dominant stability contribution from the 2D geometrical effects to the FRC compression.

4.2.Stable ignition regime

The stability criterion /S3.5κ＞ sets another boundary for the ignition parameter regime through the magnetic compression of an FRC plasma.One such example is demonstrated in figure 7,where the Lawson criterions [22,23]

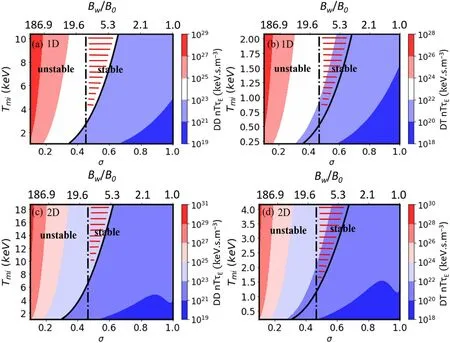
Figure 7.Contours of the fusion triple products nT Eτ as functions of the initial maximum temperature Tmi and the radial compression ratioσ or equivalently the compression magnetic field strength at wall Bw from 1D scaling laws for(a)D-D reaction,(b)D-T reaction,and from 2D MHD equilibrium for (c) D-D reaction,(d) D-T reaction with ls 0 = 2.5 m,n i0 = 3.0 × 101 9 m- 3,and Rw = 0.25 m.The black dash line denotes the /S κ stability criterion boundary and the black solid curve the lowest ignition contour line.The stable ignition regimes are shown as the red line-shaded upper triangular areas.

4.3.Limits of D-T and D-D neutron yield rates

We further estimate the upper limits on the neutron yield rates from D-T and D-D fusion reactions through FRC compression imposed by the empirical stability criterion.The neutron yield rate used herein is estimated using [25]

whereniis the ion number density,σν〈 〉is the reaction rate in cm s .3 1- For D-D reactions,the reaction rate is

whereTiis in keV.For D-T reactions,

Using the scalings forniandlsamended by the MHD equilibrium,we compare the neutron yield rates for different compression ratios and magnetic field strengths at the wall in the MHD stable regimes between D-D and D-T reactions(figure 8).The neutron irradiation power can be calculated

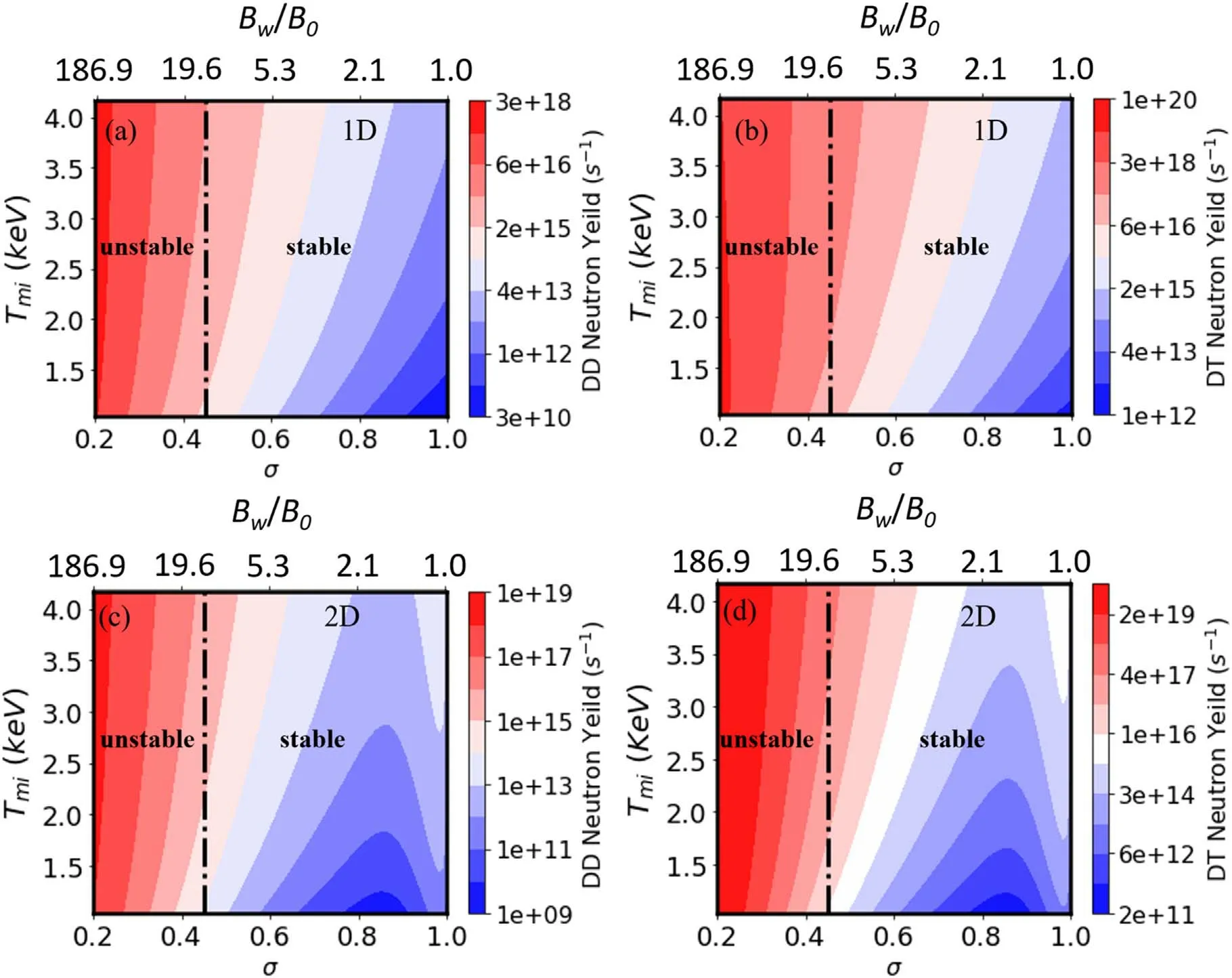
Figure 8. Contours of the neutron yield rates as functions of the initial maximum temperature Tmi and the radial compression ratioσ or equivalently the compression magnetic field strength at wall Bw from 1D scaling laws for (a) D-D reaction,(b) D-T reaction,and from 2D MHD equilibrium for (c) D-D reaction,(d) D-T reaction with ls 0 = 2.5 m,n i0 = 3.0 × 101 9 m- 3,and Rw = 0.25 m.The black dash line denotes the /S κ stability criterion boundary.

5.Summary and discussion

In summary,the scaling laws for the adiabatic compression of FRC based on 1D analytical theory have been amended using results from 2D MHD equilibrium calculations.In particular,the FRC elongation has been self-consistently determined from the G-S equation solution for any given radial compression ratio.The amended scaling for FRC elongation during magnetic compression is applied to the estimate of the upper limits for the radial compression ratio along with the empirical stability criterion for FRC.The stability regimes for fusion ignition and neutron yield rates from the approach of FRC compression are also evaluated.Under the combined constraints from FRC 2D MHD equilibrium force balance and empirical kinetic MHD stability conditions,along with the assumption that the magnetic confinement time is governed by the resistive magnetic diffusion,it is found that the FRC plasma can access the fusion ignition parameter regime through a stable quasi-static magnetic compression process,which demonstrates the physical feasibility of quasi-static magnetic compression of FRC plasma as a potential path to achieving fusion ignition conditions.These calculations may help the design of future fusion experiments and devices based on the magnetic compression of FRC plasma.

The 2D MHD equilibrium calculation for FRC during compression in this work adopts the scaling law for the maximum pressure previously derived from 1D analytical theory.We plan to develop a more self-consistent scaling law for the maximum pressure of FRC plasma during the magnetic compression entirely from the 2D MHD equilibrium and geometry of FRC in future study.

Acknowledgments

This work was supported by the National Magnetic Confinement Fusion Program of China (No.2017YFE0301805),National Natural Science Foundation of China (No.51821005),the Fundamental Research Funds for the Central Universities at Huazhong University of Science and Technology (No.2019kfyXJJS193),and the U.S.Department of Energy (Nos.DE-FG02-86ER53218 and DE-SC0018001).The authors are grateful for the supports from the NIMROD team.The author Abba Alhaji Bala acknowledges the support from the Chinese Government Scholarship.

ORCID iDs