Solving Poisson equation with slowingdown equilibrium distribution for global gyrokinetic simulation
2023-03-06QiZHONG钟奇andYongXIAO肖湧
Qi ZHONG (钟奇)and Yong XIAO (肖湧)
Institute for Fusion Theory and Simulation,Department of Physics,Zhejiang University,Hangzhou 310027,People’s Republic of China
Abstract Fusion-born alpha particles in burning plasmas are usually regarded as have a slowing-down distribution,which differs significantly from the Maxwellian distribution of thermal particles in velocity space.A generalized multi-point average method has been developed for gyrokinetic Poisson equation with slowing-down equilibrium distribution using optimization in Fourier space.Its accuracy is verified in both long and short wavelength limits.The influence of changing equilibrium distribution from Maxwellian to slowing-down on gyrokinetic Poisson equation is analyzed to illustrate the significance of the new method.The effect of critical speed in the slowingdown distribution on the field solver is also presented.This method forms an important basis for global gyrokinetic simulation of low-frequency drift Alfvénic turbulence in burning plasmas.
Keywords: gyrokinetics,Poisson solver,slowing-down distribution
1.Introduction
In gyrokinetic particle simulation,the difference between particle distribution and gyro-center distribution leads to the double gyro-average of potential field,which is manifested in polarization density [1,2].The polarization density,which is essential for the gyrokinetic Poisson equation,depends critically on the phase structure of the equilibrium particle distribution,especially for short wavelength modes.Global gyrokinetic simulations are crucial for studying many important physics issues in magnetic fusion plasmas,such as turbulent transport scaling and turbulence spreading [3-7].With the advent of burning plasmas,alpha particles inevitably excite Alfvénic turbulence with a slowing-down distribution via electron-alpha collisions [8-14].A more accurate global gyrokinetic Poisson solver with slowing-down background distribution is desirable for simulating alpha particle physics in burning plasmas and neutral beam injection heating scenarios.
The multi-point average method[2,15]is a key invention that enables global simulation of microturbulence,which has been widely used in many global gyrokinetic particle-in-cell codes [16,17].However,these global gyrokinetic particle simulations are based on Maxwellian background distribution.Some researchers have recently used so-called equivalent Maxwellian distribution,whose temperature or second order velocity moment stays the same as the slowing-down distribution [18],to simulate the turbulent transport of alpha particles,which may be valid for a number of physics scenarios that depend weakly on the phase space structure of the equilibrium distribution.Some other works [19],though correctly considering velocity space derivatives for alpha particles,have used the local flux-tube approximation to avoid tackling the global spatial dependence of the gyrokinetic Poisson equation.
In this work,a novel global method based on the multipoint average [2,15]to solve the gyrokinetic Poisson equation is developed to include slowing-down equilibrium distribution for alpha particles,and the accuracy of this new method is verified in the long and short wavelength limits.This method is useful for global gyrokinetic simulation to accurately investigate alpha particle physics in burning plasmas with the advent of International Thermonuclear Experimental Reactor (ITER)operation when the alpha particles accumulate to a non-negligible portion of the ion species.
The rest of this article is structured as follows: section 2 describes how to derive polarization density in gyrokinetics with slowing-down particle distribution; section 3 shows our numerical scheme to solve the gyrokinetic Poisson equation with the slowing-down equilibrium distribution; numerical verification is provided in section 4 for the accuracy of this new scheme;and the numerical results are summarized in section 5.
2.Gyrokinetic simulation with α particles
whereTiis the ion temperature and the double gyro-average of electric potential is defined as
Next,we show how to derive the form of polarization density for the alpha particles,i.e.npol,δαin equation (7),based on a gyrokinetic approach.Employing the Lie transform method [28],we can calculate the alpha densitynαby integrating over the velocity space on the distribution function,generated by pulling back the gyrocenter alpha distribution function=fsld+,
With these newly defined functions,the gyrokinetic Poisson equation can be written in a dimensionless form
For the typical D-T plasmas parameters mentioned before in the definition in temperature of slowing-down distribution,the polarization density of alpha particles is enhanced by the mass ratio /m miαfor long wavelengths if the equilibrium density ratio is given.However,the rationα,pol/ni,polgoes down ask⊥become larger,as shown in figure 2.
This Fourier representation is neat in form but it mixes up the configuration space and velocity space dependences through theJ0term.In reality,the background magnetic field and perpendicular temperature can vary in real space,and thenΓαwill gain global spatial dependence.Besides,the Fourier transform approach makes it more difficult to deal with realistic tokamak geometry,where no periodicity exists in the radial direction and on many occasions the global effects have to be considered seriously [3].For the Maxwellian background distribution,the multi-point/four-point gyro-average method has been developed to solve this gyrokinetic Poisson equation in real space[1,2].Here we modify this method by including the slowing-down background distributionfsldas the equilibrium distribution in the gyrokinetic Poisson equation.
3.Multi-point method for gyrokinetic Poisson solver with slowing-down distribution
The crucial part of implementing this multi-point average method for a gyrokinetic Poisson solver is to representin
We note that the Padé approximation with the Maxwellian distribution has a similar form withcα=1.In the long wavelength limit,these approximations are both very close to the exact value,as shown in figure 5,and it can be further verified by the numerical benchmarks shown in the next section.
Although the method demonstrated here is applied to the isotropic background distribution,it can also be generalized for more complex anisotropic background distributions.To obtain theΓαfunction in equation (13) for the polarization density term,we just need to perform /μ∂∂ and integrate it over velocity space with the anisotropic distribution function,which can be performed even for the numerical distribution functions.This will be carried out in our future work.
4.Numerical verification
To verify our global algorithm for the slowing-down background distribution,we shall solve the gyrokinetic Poisson equation without electron response in a largeaspect-ratio toroidal geometry tokamak with circular cross section as a sample problem.We have implemented this multi-point method for the gyrokinetic Poisson solver in Gyrokinetic Toroidal Code (GTC) by loading slowingdown marker distribution,modifying weighting coefficients and using its embedded PETSc Library for the gyrokinetic Poisson solver.The simulation domain is chosen to ber∈ [a0,a1]on the poloidal plane,witha0=0.142a,a1= 0.938aandρα/a≈ 2.51 ×10-2.In the GTC,the accuracy of gyrokinetic Poisson solver has been verified for thermal ions and electrons [31].Thus,we can verify the accuracy of gyrokinetic Poisson solver for alpha particles by ignoring contributions from the thermal ion and electron in equation(14).In the long wavelength limit equation(14)can be reduced to the following form using the Taylor expansion of :Γα
In order to compare this analytic solution with that from the four-point average method,we keep the magnetic field and temperature profile constant and thuscρis spatially uniform.If the density is given by a summation of the aforementioned eigenfunctions,then equation(14)can be solved analytically.Here we sum up three eigenfunctions withm6,= and different radial wavelengths atkrρc= 1,1.5,2,and corresponding amplitudes to 1,0.5 and0.2 respectively.Figures 7 and 8 show the 1D and 2D plots for the numerical solutions from the four-point average method and Padé approximation,respectively.The globally averaged differences between the numerical methods and the analytic solution are about 1%and can be ignored.Figure 7 also shows the solution from the original four-point average method with an equivalent Maxwellian with the same temperature as the slowing-down distribution,i.e.the orange dotted-and-dashed line.This numerical solution deviates from the analytic solution with an overall error of more than 6%.The amplitude of the solution using the four-point average method is slightly larger,which can be ascribed to the fact that the operator of the four-point average is larger than the Padé approximation inkspace,as shown in figure 4.Though not so precise inkspace,the Padé approximation still gives a solution as good as that from the four-point average method in this case.This suggests that we may not need to be very accurate at largek ρα⊥since the polarization density is nearly identical to the adiabatic response in the short wavelength limit,regardless of the particle’s velocity distribution.
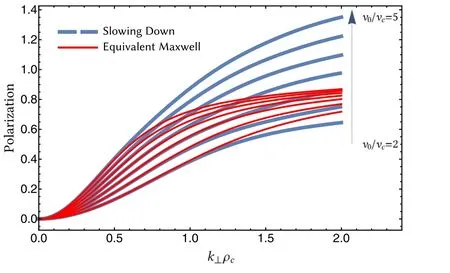
Figure 1.Polarization comparison between slowing-down distribution and equivalent Maxwellian in k-space.The blue dashed line is for the slowing-down distribution and the red solid line is for the equivalent Maxwellian distribution.The lines from bottom to top correspond to various ratios of v 0 /vc ranging from 2 to 5 with a step size of 0.5.
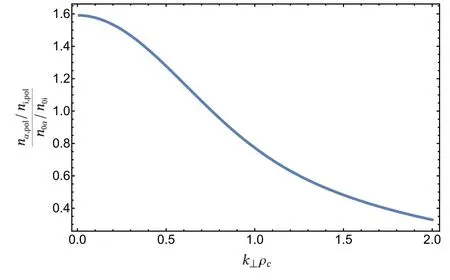
Figure 2. Polarization density ratio between alpha particles and thermal fuel ions varying in k space,normalized by their equilibrium densities respectively.
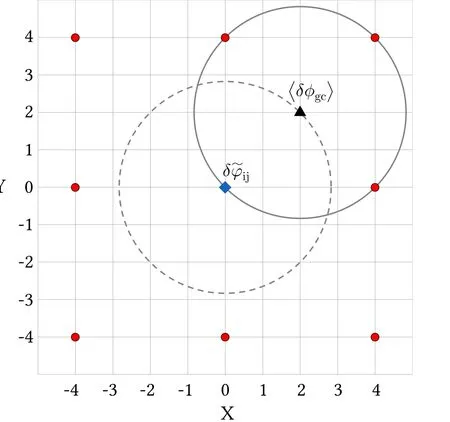
Figure 3.Scheme for calculating at grid point i j,.

Figure 4.ExactΓα function (blue solid line) and its numerical approximations vary with perpendicular wavelength k⊥ ρc:4-point average method with three velocity nodes in the integration (red dotted line),and Padé approximation (black dashed line).

Figure 5.Comparison of analytic expression and numeric solutions using four-point average approximation and Padé approximation for the gyrokinetic Poisson equation in the long wavelength limit with k r ρ i= 0.11and m =6.

Figure 6.2D poloidal contours for solutions to different operators to the gyrokinetic Poisson equation in the long wavelength limit:(a)four-point average operator,(b)Padé approximation operator,where k r ρ i= 0.11and m = 6.The differences between these two solutions are shown in(c).

Figure 7. Comparison of analytic solution (blue solid line) and numeric solutions using the new four-point average method with slowing-down equilibrium (red X marker),original four-point average method with equivalent Maxwellian equilibrium (orange dotted-and-dashed line)and Padé approximation (black long dashed line) for the gyrokinetic Poisson equation in the short wavelength limit.
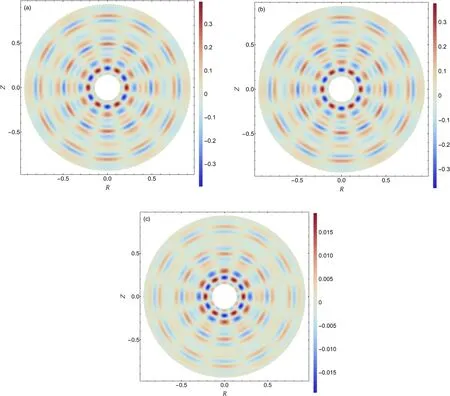
Figure 8. 2D contour of the solution to gyrokinetic Poisson equation in the short wavelength limit on the poloidal plane.The numerical methods used in solving the Poisson equation are the (a) four-point average method and (b) Padé approximation.The difference between them is shown in (c).

Figure 9.Solutions to an arbitrary density source with a dominant wavelength k r ρc ~ 1with different energetic alpha particle fraction from 5% to 20%.
Finally,we investigate how the fraction of energetic particle affects the gyrokinetic Poisson solver.Here we assume that the main ions are a 50%-50%mixture of D and T with a temperature of 10 keV,and the energetic particles are the fusion-born alpha particles with a slowing-down distribution.The density term is the same as that in the above short wavelength verification wherekrρc~ 1and in this casekrρi≪1.The solutions are shown in figure 9 with different energetic particle fractions from 5% to 20%.The difference could be significant whenn α/neincreases above 5%,as demonstrated in the figure.
5.Conclusion
A real space gyrokinetic Poisson solver for slowing-down equilibrium distribution has been developed based on the multi-point average method [2,15]and verified for its accuracy in the long and short wavelength limits.The discovery process for this method is shown in detail and it can be further modified to accommodate more complicated equilibrium distributions.This method can be incorporated into the global gyrokinetic particle simulation to study the crucial alpha particle physics in the burning plasmas,i.e.to simulate the drift Alfvénic turbulence accurately in the presence of slowing-down alpha particle distribution.
Acknowledgments
This work is supported by the National Magnetic Confinement Fusion Program of China (No.2015GB110000),and by National Natural Science Foundation of China(No.11975201).
ORCID iDs
杂志排行
Plasma Science and Technology的其它文章
- Efficient combination and enhancement of high-power mid-infrared pulses in plasmas
- Realization of Te0>10 keV long pulse operation over 100 s on EAST
- Experimental studies of cusp stabilization in Keda Mirror with AXisymmetricity (KMAX)
- BITS: an efficient transport solver based on a collocation method with B-spline basis
- Comparing simulated and experimental spectral line splitting in visible spectroscopy diagnostics in the HL-2A tokamak
- Optimization of X-mode electron cyclotron current drive in high-electron-temperature plasma in the EAST tokamak
