基于边缘计算的高渗透率微电网并行分布式优化经济调度

聂涌泉，彭超逸，胡亚平，何宇斌，马光，黄楚鸿

（1. 中国南方电网有限责任公司电力调度控制中心， 广州 510663； 2. 中国能源建设集团广东省电力设计研究院有限公司， 广州 510663）

0 引言

新能源具有可持续性和环境友好性，使用风力、光伏等新能源发电是减少碳排放的有效方式，因此新能源发电技术已经成为各国关注的焦点［1-2］。与此同时，新能源发电可以解决大部分发展中和发达国家都在遭受能源短缺的问题［3-4］。为了提高可再生能源的渗透率，将可再生能源发电进行规模化组合形成微电网，并利用控制中心对其进行控制与调度，大大降低了可再生能源的波动性对大电网的影响，提高了供电可靠性［5］。大电网与合适的控制方法相结合，被国内外许多专家学者认为是降低能耗、提高电力系统可靠性可靠性和灵活性的主要方式［6］。微电网的运行方式主要分为并网和离网两种，对于包含海量分布式可再生能源的微电网而言，采用并网运行方式可以提高系统运行稳定性［7］，并网运行时为了给微电网留出足够安全裕量，协调控制微电网内部分布式电源来平抑关口变压器功率输出［8］。

边缘计算是靠近端侧设备或数据源头的本地计算，具备实时采集、即时计算、在线响应和准确控制等优点［9］。基于边缘计算的微电网控制方法可以确保信息流处理的实时性，进而保证能量流控制的稳定性，近来已得到广泛关注［10］。文献［11］结合边缘计算和深度强化学习，提出一种微电网能量调度方案，考虑边缘计算服务器任务载量的同时对原问题进行了分解，实现了微电网供电计划的分布式求解。文献［12］基于多接入边缘计算对微电网进行能源调度，考虑可再生能源预测和能源消耗的不确定性，提出一种具有风险意识的微电网能源调度方法来最小化调度方案实际的能量剩余。文献［13］提出了一种具有边缘计算能力的自供电无线网络能量调度机制，建立了系统总能耗最小的两阶段线性随机规划模型，实现了电网的经济调度。文献［14］提出一种基于云-边缘计算架构的海岛微电网经济调度策略，通过启发式算法生成最优决策样本并采用监督学习模型进行训练，实现了孤岛微电网的实时经济调度。

在过去10年中，很多学者对微电网的控制做了大量研究，所提出的控制方案主要有3 种类型，即分层控制［15-18］、集中控制［19-22］以及分散或分布式控制［23-26］。分层控制包括主控制、二次控制，有时包括三次控制，其中分布式电源（distributed generator，DG）由主控制调节，而主控制引入的偏差由二次控制消除。

在集中控制中，有一个中央控制器收集并处理所有信息，因此无需迭代即可获得最优解。文献［27］根据发电机稳态模型，以最小化运行成本与最大化环境效益为目标函数，提出了一种基于集中控制策略的调度模式。文献［5］以最大化发电收益为目标函数，提出了一种互联微电网集中式预测模型，实现了集中控制下微网的发电机最大资源收益。文献［28］提出了一种集中式一致性算法，运用总功率偏差作为收敛条件，在总功率偏差的计算中对当前所有的发电机输出功率进行求和再进行运算，从而解决了对每个区域的功率调度问题，然而单点故障将导致整个系统故障。

另一方面，在分散控制或分布式控制中，仅使用局部信息，即使多个控制器失效，系统仍然可以工作。为了降低通信和计算的复杂性，分散或分布式控制似乎更适合复杂系统。由于微电网的分布式特性，利用相邻单元之间的沟通和信息交流可以提高信息传输的效率。因此，近年来，微电网的分布式控制和分布式优化调度方法，已成为研究的热点。

文献［29］基于传统的下垂控制提出了一种交流电网的最优功率控制策略，应用等微增率原理满足系统的经济调度要求。文献［30］以发电机最小成本为目标函数，提出了一种完全分布式算法来解决有向网络上的微电网经济调度问题，该算法使得每个处理器可以进行本地分配权重，并且在考虑了噪声和传输延迟的情况下实现了最优调度。文献［31］提出了一种基于一致性的分布式微电网控制方案，将频率控制与图论中的一致性协议相结合，采用PI频率控制器和神经网络频率控制器开发经济调度方法，并且提出了鲁棒经济调度控制方法，使得系统在通讯失败的情况下也能保持最佳调度，在实现经济调度的同时提高了系统鲁棒性。文献［32］提出了一种基于混合整数规划微电网分布式发电经济调度策略，使用分段线性的方法产生可行解和区域解的下界，从而实现更快速和准确的计算。文献［33］提出了一种交直流微电网群的分布式控制调度方法，根据离散一致性原则对电流变换器进行控制，从而实现各个交直流微电网之间的功率分配，从而达到最优经济调度的目的。文献［34］提出了一种混合连接微网的经济调度策略，该方法充分考虑了可再生能源与负荷的波动，在多网络连接的拓扑结构中有着更高的鲁棒性。

一致性算法可以以分布式方式解决成本最小化的经济调度问题。然而，对于更一般的优化问题，找到一个变量来达成一致并不容易。在这种情况下，交替方向乘子法（alternating direction method of multipliers，ADMM）能够以一种分布式的方式进行一般优化问题的快速求解［35］。ADMM 早在上世纪七十年代就由Gabay 和Mercier 等人提出，最近又由Stephen Boyd 进行整理，成为一种求解具有可分结构的凸优化问题的重要方法［36］。ADMM 同时具备对偶分解法和增广拉格朗日法的优点，既能够将原问题分解为多个子问题来进行分布求解，又放宽了对目标函数必须为凸函数且可导的严格要求。因此，该算法已经被广泛应用于求解各类可分凸优化问题［37］。文献［38］使用二阶锥松弛方法以及同步型ADMM 算法作为模型上层搭建多微网的主动配网分布式双层优化调度策略，有效地实现了系统的最优运行，提高了系统的经济性。文献［39］使用ADMM 算法将全局变量转化为局部变量，并以满足局部变量为基础，进而推进满足全局变量优化，解决了多微网运行之间的个体变量矛盾，高效解决了多微网的联合经济调度，减少了运行成本。

综上所述，ADMM是一种广泛使用的分布式优化方法，结合边缘节点天然分布式特性，可以在边缘计算分布式平台上得到充分利用。但是，标准的ADMM是串行工作的，这意味着每一个边缘节点要等上一个边缘节点更新完成后，才开始计算和更新。对于一个多变量的复杂优化问题，随着优化问题规模的增大，这样的串行求解过程可能会导致ADMM需要更多的迭代次数来寻找最优解。如果分布式优化方法并行工作，信息可以在多个边缘节点之间交换和处理，各边缘节点可以同时（并行）搜索其子问题的解空间，从而加快迭代寻优的收敛速度。

基于边缘计算分布式优化框架，本文提出了一种并行ADMM方法，所有边缘节点并行对子问题的决策变量进行更新求解，并将求得的本地中间解与邻接的边缘节点进行交换，在反复迭代的过程中，逐步得到优化问题的全局最优解。在不降低优化精度的前提下，改进的ADMM 算法比标准ADMM算法收敛更快。进一步，融合边缘计算信息网络，建立微电网信息-能量双层模型，将该方法应用于求解微电网经济调度问题。仿真结果表明，求解相同的优化问题，并行ADMM 算法的迭代次数仅为标准ADMM 算法的二分之一甚至更少。求解含海量可再生能源微电网发电成本最小优化调度时，各可控DG 的增量成本趋于一致，表明此方法能够使得微电网运行成本最小化。

1 基于边缘计算的改进并行ADMM

首先介绍了边缘计算的概念并描述了其对应信息网络分布式求解的流程，接着介绍了标准ADMM 算法串行求解可分解优化问题的计算步骤并提出了一种改进的并行ADMM 算法用于分布式地求解优化问题。

1.1 边缘计算与信息网络

边缘计算是指靠近网络边缘侧数据源头，融合网络、感知、计算、存储、分析等核心应用能力的分布式开放平台。边缘计算依托于靠近端侧设备的边缘节点（Node）对数据进行感知和本地计算，并通过分布式组建的信息网络在平台内分享信息，从而在保证信息流实效性的基础上提供稳定的服务。边缘节点组建的分布式信息网络如图1所示。

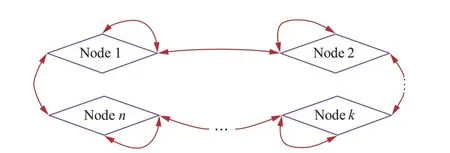
图1 边缘计算信息网络Fig. 1 The information network of edge computing

边缘计算框架要求信息网络中的边缘节点作为对等节点能够实现双向通信以提升整个通信过程的协同性。D2D（device-to-device）通信技术是实现智能代理之间的横向通信且无需占用过多公共通信资源的一种优势技术［40］。本文选择D2D 通信技术作为边缘计算框架的通信基础，忽略时延、丢包等问题认为在迭代求解过程中边缘节点之间可以理想地共享信息。

式中：F（x）为总目标函数；x∈Rn×1；A∈Rm×n；B∈Rm×1；f(xi)为凸函数；n为节点数量。

原问题F（x）经分解后，可以得到每个边缘节点对应的子问题f（xi）及子决策变量xi。优化问题求解过程中，Nodei可以感知xi的当前状态并进行本地计算，之后Nodei与邻接的其余边缘节点进行信息共享并根据共享得到的信息对本地计算结果进行修正，依托于边缘计算信息网络天然的分布式特性，优化问题得以在满足全局约束的条件下实现分布式的求解。

1.2 改进的并行ADMM

式（1）对应的增广拉格朗日函数Lρ为：

式中：y为拉格朗日乘子组且y∈Rm×1；ρ为惩罚因子且ρ＞0。

采用标准ADMM 算法，各变量依次进行交替求解的计算步骤如式（3）所示。

式中：k为迭代次数；xk，i为第k次迭代中第i个节点接收到的上一个节点更新过的本地决策量；xik+1为第k次迭代更新后第i个节点的值；yk为第k+1 次和第k次迭代更新后的拉格朗日乘子组。

采用标准ADMM 求解时，每个边缘节点根据式（3）更新完本地的决策量后，都会用更新后的本地决策量来替代更新之前的值并传送给下一个边缘节点，即xk，i为：

所有的决策量根据式（4）更新完成后，利用本次迭代更新完的决策量来统一更新拉格朗日乘子，完成本轮迭代。更新后的拉格朗日乘子在下一次迭代更新过程中依次传递。因此，第k次迭代中第i个边缘节点更新时接收到的由上一个可控DG 边缘节点发送的信息为：

采用标准ADMM 对上述可分解优化问题进行串行求解时，当某一个边缘节点更新本地决策变量时，环形信息网络中其余所有边缘节点均处于等待状态，造成计算资源的浪费和求解时长的增加。如图1 所示，环形信息网络中边缘节点之间的通信链路是双向的，改进ADMM 算法使所有边缘节点可以并行地更新本地决策变量，并将更新后的中间解与邻接的边缘节点进行交换，可以提高求解效率。在上层环形信息网络中，采用改进ADMM 算法，各边缘节点并行求解的计算步骤如式（6）所示。

采用改进ADMM 算法求解时，上层环形信息网络中每个边缘节点在进行迭代计算前会收到左右两个邻接边缘节点发送来的上一次迭代完成的中间解。上层信息网络中边缘节点的数量为n时，第k次迭代计算前第i个边缘节点接收到的来自左右两个邻接边缘节点发送的中间解汇总后分别如式（7）所示。

式中si（j）为环形信息网络中第j个边缘节点到第i个边缘节点的通信距离。

若两个相互邻接的边缘节点之间的通信距离为1，则环形信息网络中编号为j的边缘节点到编号为i的边缘节点的通信距离可表示为：

在第k次迭代中，第i个边缘节点更新完本地的决策变量后，将xik+1与xk，i进行整合得到-xk，i，用于进一步更新可以表示为：

如式（9）所示，各边缘节点利用更新完的中间解并行地更新本地的拉格朗日乘子，并将更新后的本地拉格朗日乘子与中间决策变量发送给邻接的边缘节点。因此，在第k次迭代前，第i个边缘节点接收到的由左右两个邻接边缘节点发送的信息为：

在下一次迭代开始前，每个边缘节点利用接收到的信息，将邻接边缘节点发送的本地拉格朗日乘子与自身的本地拉格朗日乘子进行融合，确保迭代运算的结果收敛到全局最优值。

2 微电网信息-能量双层模型

为了对微电网中分散的电气设备进行实时的就地分布式控制，借助边缘计算理论，本文提出一种基于边缘计算的微电网信息-能量双层优化结构，其中包括由边缘节点组成的上层信息网络和由微电网终端设备连接而成的下层能量网络。下层能量网络由分布式电源和负载组成，分布式电源包括光伏、风机、微型燃气轮机和小型柴油发电机等；上层信息网络中包含各类终端DG对应的边缘节点，边缘节点就地对终端DG 的出力进行感知、计算分析和控制。具体的微电网信息-能量双层优化结构如图2 所示，图中上层信息网络中的边缘节点由菱形框表示，有向箭头用来表示各边缘节点之间的通信链路及其方向。边缘节点通过虚线双向箭头对物理网络中DG的出力进行感知和控制。

图2 双层网络的微电网分布式控制模型Fig. 2 Two-layer distributed control model for microgrids (MGs)

为了最大限度消纳海量分布式可再生能源，降低并网微电网的碳排放量，使光伏、风机等分布式电源工作在最大功率点追踪方式（maximum power point tracking，MPPT），此时其功率输出不能人为地调整，故称其为不可控DG；微型燃气轮机、小型柴油发电机等可以根据需要人为地调整其功率输出，工作在PQ模式，称为可控DG；微电网并网运行时，微电网中的公共耦合节点（point of common coupling，PCC）通过关口变压器与上级电网交换瞬时波动功率来提供电压和频率的支撑，随后PCC处的交换功率被其他可控DG 分担。微电网通过与上级电网互动调控使微电网在留有较大安全裕量的同时实现稳定运行。

信息网络中对应PCC的边缘节点通过感知微电网中PCC当前的功率输出，获得微电网当前时刻的功率波动，并将这一信息传递给邻接可控DG 对应的边缘节点，即PCC对应的边缘节点只有出边没有入边。可控DG 对应的边缘节点，在对信息进行计算处理后，通过双向的通信链路与邻接的边缘节点进行信息共享已完成经济调度的分布式求解，因此其同时具有出边和入边。如图2 所示的上层信息网络，可控DG 对应的边缘节点依次按顺序成环形连接，确保后续分布式求解优化问题时结果能够收敛到全局最优。

3 微电网优化经济调度模型

首先建立了并网微电网发电成本最小的优化调度模型，之后在建立的微电网信息-能量双层模型的上层信息网络中，结合边缘计算的分布式优化框架，利用本文改进的ADMM 算法，推导出了微电网发电成本最优调度时各可控DG 出力的迭代计算公式。

3.1 优化经济调度模型

微电网并网运行时，其经济调度的主要任务是实现内部分布式电源发电成本的最小化，当风机、光伏等可再生能源按照最大功率跟踪模式输出时其发电成本可以忽略不记，则微电网的发电成本主要由微型燃气轮机等可控DG 的发电成本构成［41-43］。微型燃气轮机等可控DG 的发电成本函数通常可以近似表示为其输出有功功率的二次函数［44］，此外可控DG 发电产生碳氧化物的治理成本可以用其需要缴纳的碳税来衡量，当单位碳税价格已知时，碳氧化物的治理成本可以表示为输出有功功率的一次线性函数［45］，则微电网优化经济调度的目标函数可以表示为：

式中：ncg为微电网中可控DG的数量；Fi为第i台可控DG 的优化目标函数；Ci（·）为第i台可控DG 的发电成本函数；Ei（·）为第i台可控DG 发电产生碳氧化物的治理成本函数；Pcg，i（t）为第i台可控DG在t时刻的发电功率。

可控DG 的发电成本函数和碳氧化物治理函数分别如式（12）所示。

式中：αi、βi和γi分别为第i台可控DG 发电成本的一次、二次和常数项系数；egas为单位碳税成本系数。

当t时刻微电网中以可再生能源驱动的DG 出力或者负荷需求突然发生变化时，PCC 立即通过关口变压器与上级电网进行功率交换，维持微电网的电压和频率稳定，因此在t时刻微电网中PCC 的出力如式（13）所示。

式中：PL（t）为微电网在t时刻的负荷需求量；Pre，i（t）为第i台可再生能源在t时刻的发电功率；PPCC（t）为微电网中PCC 在t时刻的交换功率；nre为微电网中可再生能源发电机数量。

为了在外部环境或负荷需求发生突变时，微电网能够拥有较大的调节能力，微电网根据PCC与上级电网交换功率值对可控DG 输出进行调控，即微电网中可控DG的功率输出需满足式（14）约束。

此外，微电网中的可控DG，其任一时刻的功率输出存在上下限，如如式（15）所示。

式中：Pcg，i，min和Pcg，i，max分别为第i台可控DG 的发电功率下限和上限。

第i台可控DG 的功率输出限制即其在t时刻的爬坡速率限制如式（16）所示。

式中：dPcg，i，down和dPcg，i，up分别为第i台可控DG 的最大下坡速率和最大上坡速率。

3.2 基于改进ADMM的优化模型求解

并网微电网发电成本最小优化模型如式（17）所示。

记t时刻优化求解得到的第i台可控DG 的出力Pcg，i（t+1） =Pcg，i，则考虑等式约束时，根据边缘计算分布式优化框架，利用改进ADMM 算法求解微电网发电成本最小的迭代公式如式（18）所示。

式中：Pcgk，i为第i个可控DG边缘节点在第k次迭代前接收到的邻接可控DG 边缘节点发送的可控DG出力中间解；为第i个可控DG 边缘节点在第k次迭代中更新完本地可控DG 出力后的中间解；-1为元素全为1 的ncg维列向量；Pcg（t）为t时刻可控DG出力组成的列向量。

根据式（18）完成每次迭代后，各可控DG 边缘节点根据式（15）—（16）所示的上下限约束来进一步确定本次迭代中间解的最终值。

4 算例分析

首先基于MATLAB/Simulink建立了含海量可再生能源微电网仿真平台，之后通过对典型可分解凸优化函数进行求解，对比测试了标准ADMM 算法和改进ADMM 算法的求解性能，最后在微电网仿真平台上采用改进ADMM 算法对可控DG的发电成本最优调度进行了求解。

4.1 微电网仿真平台

为了测试改进ADMM 算法求解微电网发电成本最优的有效性，在Matlab/Simulink 环境下搭建了包括11 个DG 及其负荷的放射型并网微电网仿真平台如图3所示。其中，6台可控DG 的发电成本系数如表1所示。

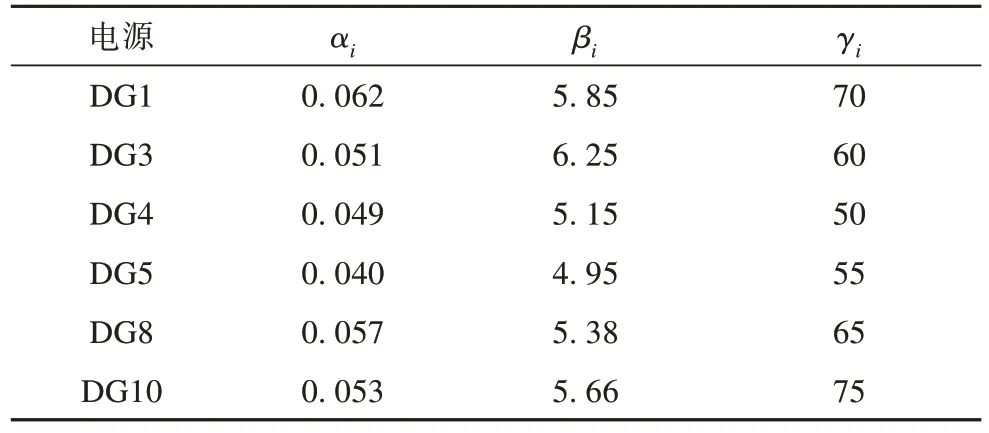
表1 可控DG发电成本系数Tab. 1 Generation cost coefficients for controlled DGs

图3 微电网仿真模型Fig. 3 Simulation model for MGs

微电网内各DG 的容量及其运行方式，以及其对应的负载最大需求如表2所示。

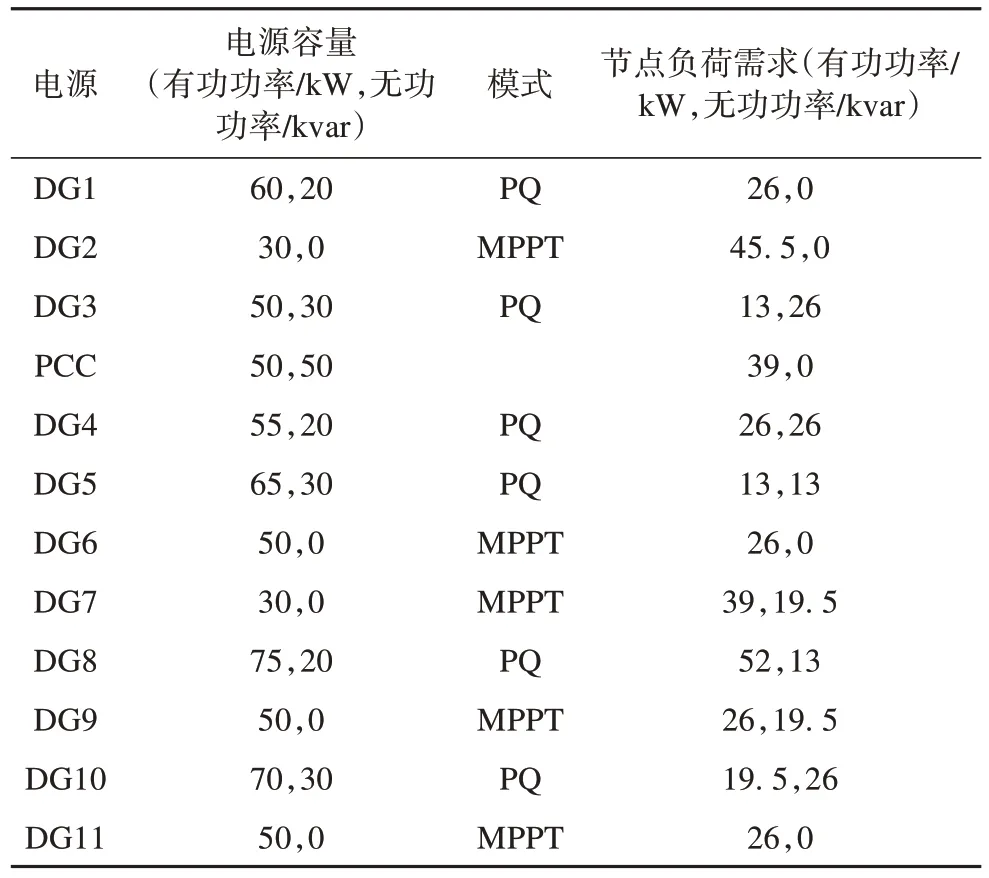
表2 DG和负载参数Tab. 2 Setup and parameters of DGs and loads

4.2 算法对比

为了测试所提改进ADMM 算法的性能，本算例对比测试了标准串行ADMM 和改进并行ADMM在边缘计算分布式优化框架下求解的精度和收敛速度。选用如表3 所示的4 种典型凸函数作为目标函数，来对两种算法进行比较测试。

表3 测试函数表Tab. 3 Tables of test functions

为了消除随机性对算法求解性能的影响，在每种测试目标函数下分别设置100 组系数不同的等式约束条件分别利用标准串行ADMM 和并行ADMM求解，再将相关的性能指标做平均来做比较。等式约束中优化变量对应系数取值式（19）所示。

同时，等式约束常数项的取值应保证所构造优化问题最优解的存在。

以内点法求解的结果作为参考最优解，计算标准ADMM 和改进ADMM 算法所求出最优解与参考最优解的绝对平均偏差（mean absolute errors，MAE）来比较两者求解精度。MAE 的计算公式如式（20）所示。

式中：xi*，IPA为内点法计算得到的参考最优解的第i个分量；xi*为边缘节点利用标准ADMM 或改进ADMM计算得到的第i个子问题的最优解。

标准ADMM 和改进ADMM 算法的惩罚因子设置相同均为0.05，收敛精度均取0.01，则在所设置的100组约束条件下消除随机性后利用标准ADMM算法和改进ADMM 算法求解上述表中所示典型凸优化问题得到的最优解与内点法参考最优解的绝对平均偏差MAE 以及所需迭代次数（number of iteration，NoI）如表4所示。

表4 串行ADMM与并行ADMM结果对比Tab. 4 Results comparison berween serial ADMM and parallel ADMM

由表4 可知，在边缘计算分布式优化框架下采用标准ADMM 算法和本文改进的ADMM 算法对测试的优化问题求解时，MAE 值很小，得到的最优解与采用内点法得到的参考最优解基本一致。其中，对同一测试函数纵向对比来看，当n值增大即问题复杂度提高时，采用两种算法求解的迭代次数都会增加。此外，横向对比来看，分别采用标准ADMM 算法和改进ADMM 对同一优化问题进行求解时，改进ADMM 算法求得的最优解精度更高，且迭代次数更少收敛速度更快。测试第一类函数时，改进ADMM 算法的迭代次数仅为标准ADMM算法的三分之一；测试第二类函数时，改进ADMM算法的迭代次数仅为标准ADMM 算法的二分之一；测试第三类函数时，改进ADMM 算法的迭代次数最小为标准ADMM 算法的四分之一；测试第四类函数时，改进ADMM 算法的迭代次数平均最小为标准ADMM算法的十分之一。

此外，根据事前分析估算法可以计算出单次迭代过程中本文所提并行ADMM 算法与标准ADMM算法的空间复杂度，包含存储执行代码和预分配变量的内存在内，若最大允许迭代次数为Tmax，则两者的单位空间复杂度都可以近似表示为O（nTmax+n）。结合上述利用事后统计法对比迭代次数的结果可知，在单位空间复杂度近似相同的情况下，本文所提的并行ADMM 算法相对于标准ADMM 算法而言在时间复杂度对比上仍然具有优越性。

4.3 成本最小

仿真过程中，微电网内高比例风机和光伏的出力曲线以及微电网内负荷总的有功需求和无功需求分别如图4和表5所示。

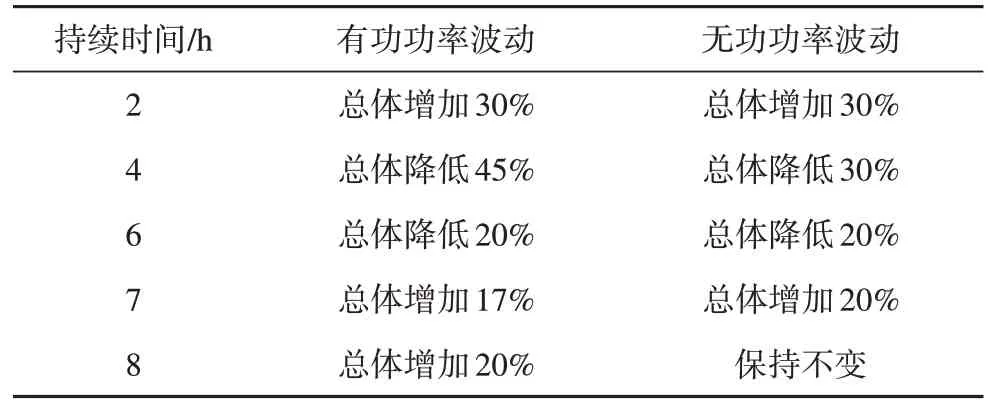
表5 负荷需求波动Tab. 5 The fluctuations of the loads demand

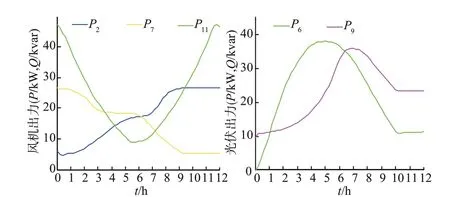
图4 微电网仿真环境设置Fig. 4 The simulation environment setting for MGs

在建立的微电网仿真平台中，上层信息网络中边缘节点利用式（20）所示的并行ADMM 求解公式来对孤岛运行微电网发电成本最小优化调度进行求解，在调度周期内各可控DG 的出力曲线如图5所示。

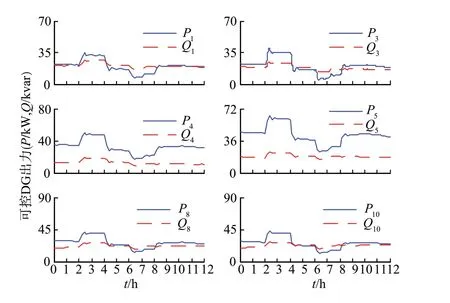
图5 可控DG出力曲线Fig. 5 The output curve for controlled DGs

如图5 所示，t=2 h 之前微电网内没有较大的功率波动，各可控DG 的出力没有较大变化，且如图所示各可控DG 对应的耗量微增率始终保持相等，微电网内可控DG的出力实现了经济最优。

在t=2 h，微电网内部负荷需求突然急剧增大，此时如图6 所示，微电网的电压和频率受到影响从而发生较大波动。

图6 微电网电压和频率曲线Fig. 6 The voltage and frequency curve of MGs

如图7 所示，微电网调控PCC 及时从上级电网汲取功率，从而保证微电网的电压和频率稳定且不会越过安全限制。之后PCC对应的边缘节点感知从上级电网汲取的功率值，并在信息网络中与可控DG 对应的边缘节点进行共享，可控DG 边缘节点并行进行更新，通过控制可控DG 增发功率来分担储能系统的放电输出，如图8 所示，增发功率后各可控DG 的耗量微增率仍然保持一致，微电网内的发电成本实现了经济最优。

图7 PCC出力曲线Fig. 7 The output curve for PCC

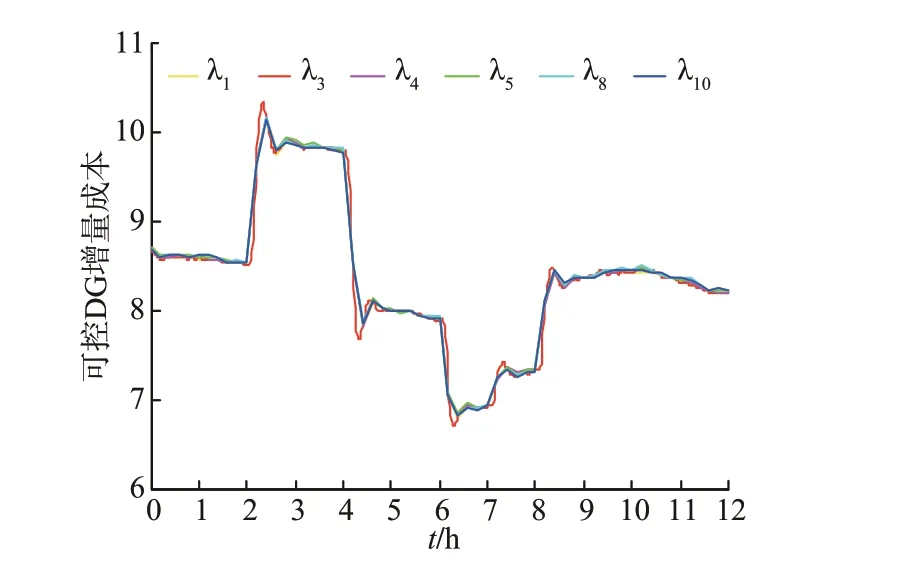
图8 可控DG耗量微增率曲线Fig. 8 Incremental ratio of consumption curves for controlled DGs

在t=4 h，微电网内部负荷需求突然大幅度减小，此时如所示微电网的电压和频率受到影响发生较大波动。如图7 所示，微电网调控PCC 及时通过关口变压器向上级电网输送功率来消纳微电网内多余的电量，进一步稳定微电网的电压和频率。之后各可控DG 按照对应边缘节点更新的控制指令来减发功率，通过微电网与上级电网的互动调控使PCC的功率波动为零，如图8 所示，减发功率后各可控DG 的耗量微增率仍然保持一致，微电网内的发电成本实现了经济最优。

其余时刻，当微电网内部的负荷需求突然减小或增大时，微电网通过与上级电网互动调控使PCC及时通过关口变压器向上级电网汲取或释放功率，从而维持微电网电压和频率的稳定。之后PCC对应的边缘节点将感知到的关口变压器交换功率与信息网络中其余的边缘节点进行共享，各可控DG 对应的边缘节点在上层信息网络中采用改进的ADMM算法对各自出力的大小进行分布式的求解，在保障微电网留有较大安全裕量的基础上实现了经济最优。

5 结论

基于边缘计算的分布式优化框架，本文提出了一种用于含海量分布式可再生能源微电网能量管理的并行分布式优化方法，在并网微电网与上级电网互动调控的前提下实现微电网的经济调度，其目的是提高分布式优化方法的收敛速度。因此，对标准ADMM 的串行求解方式进行改进，在本文提出的并行ADMM 方法中，边缘节点在本地并行地对优化问题进行求解，并将求得的局域优化结果与邻接的边缘节点进行共享，在边缘计算的分布式框架下反复迭代，从而逐步获得优化问题的全局最优解。此方法在不降低优化精度的前提下，可以提高算法收敛速度。进一步，搭建含海量可再生能源微电网的优化调度模型，将该方法应用于求解微电网经济调度问题。

在MATLAB/Simulink 中搭建微电网仿真平台，从仿真结果可以得到下面的结论。首先，将并行ADMM 求得的最优解的精度与使用IPA 和标准ADMM 得到的结果进行了比较，结果表明这三种方法得到的最优解几乎相同。其次，求解相同的可分解优化问题时，本文所提的并行ADMM 算法的迭代速度要远快于标准ADMM 算法，前者的迭代次数仅为后者的二分之一甚至更少。最后，采用设计的并行分布式方法对含海量分布式可再生能源微电网的优化调度问题进行求解，仿真结果表明，在并网微电网与上级电网互动调控的前提下，微电网可以在保留较大安全裕量的同时实现稳定运行，且微电网内分布式电源的增量成本一致，即微电网运行成本最小实现了最优调度。