高强度钢方管局部感应加热数值模拟及实验研究

王 宇， 刘 靖， 马晓燕， 韩静涛,

(1. 北京科技大学 材料科学与工程学院，北京 100083；2. 欣诺冷弯型钢产业研究院(曹妃甸)有限公司，河北 唐山 063200)

高强度钢方管作为一种绿色环保的轻量化材料，通过减小自身截面尺寸和质量，降低焊接和涂装工作量，减少能源和资源消耗，在汽车轻量化和钢结构建筑等领域应用广泛.然而，高强度钢室温下屈服强度高，在发生塑性变形时的流动应力、最小弯曲半径和回弹量较大[1]，导致成形后的尺寸精度差[2]，且容易在弯角处出现裂纹[3].高强度钢方管的主要塑性变形区域为圆角，在辊压成形过程中存在厚度减薄缺陷和冷作硬化效应[4]，4个圆角的外形尺寸难以统一.为了避免出现角部裂纹，高强度钢方管需要采用更大的圆角半径，但会减小方管的应用范围，同时增大焊接难度和工作量.

为了克服高强度钢方管的冷成形难题，改善圆角区域的几何尺寸和组织性能，彭雪锋等[5]在冷辊压成形工艺基础上，提出局部热辊压成形工艺，在成形道次之前增添加热装置，对高强度钢普通方管(下文中简称“方管”)进行二次辊压成形，目的是将上述不均匀的4个圆角成形为圆角半径极小的“尖角”，同时克服厚度减薄缺陷和冷作硬化效应.感应加热技术具备加热速度快、加热效率高、环境污染小等优点，可以满足局部热辊压成形工艺的技术要求.选用合适的感应加热工艺参数，在圆角区域迅速获得适宜温度的透热，是得到理想高强度钢尖角方管(下文中简称“尖角方管”)的重要前提.

由于目前的测量手段难以获得坯料表层以下的温度分布，所以学者们对感应加热技术中温度场的研究多是借助有限元法.马骏等[6]通过数值仿真，完成小型可变气隙直流感应加热器样机的建模，探索不同加热条件与铝棒加热分布间的关系.Guo等[7-8]分别建立圆管和方管的变曲率局部感应加热弯曲成形工艺有限元模型，前者发现轴向推进速度和加热工艺参数对成形结果影响显著，后者研究了芯棒对成形质量和成形极限的影响.Wang等[9-11]分别将局部感应加热技术应用到水火弯板和齿轮轧制工艺中，前者通过热弹塑性分析，研究了不同工艺参数对钢板弯曲结果的影响，后者通过分析温度场结果，对加热线圈的结构进行了优化，同时减轻成形缺陷，提高了成形精度.此外，研究表明，在加热线圈上安装导磁体可以增强局部感应加热效果[12]，不同几何尺寸的导磁体对加热速率和温度分布均匀性也有显著影响[13].

尽管不少学者已经对感应加热技术进行了数值模拟研究，但绝大多数研究重点仅为温度场，而电磁场作为影响温度场的根本源头，相关研究很少.与此同时，很多数值模拟研究缺乏相应实验验证，而测温枪作为目前最常用的测温仪器，只能进行单点温度捕捉且准确度不高.彭雪锋等[5]选用700 ℃作为最高热成形温度，成形后的方管外圆角半径为2 mm，约等于板带厚度，但是内圆角处萌发了大量微小裂纹，在后续工程应用中存在安全隐患，这表明加热工艺参数有待进一步优化，否则无法彻底解决高强度钢成形难题.

为了进一步提升高强度钢方管“尖角化”效果，即大幅减小外圆角半径并消除裂纹缺陷，同时避免传统“试错法”造成的资源浪费，本文建立局部感应加热辊压成形工艺的电磁-温度场耦合模型，从电磁场角度揭示温度场变化的根本原因，对加热工艺参数进行系统性优化.采用数值模拟优化后的加热工艺参数开展实验研究，并利用红外热像仪对整个加热区域进行高精度的温度捕捉，验证有限元模型的预测精度.

1 数学模型

1.1 电磁场模型

局部感应加热辊压成形工艺中，方管加热的基本电磁场理论是麦克斯韦方程组，它由4个方程组成，微分形式如下[14]：

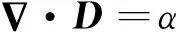
(1)

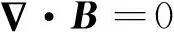
(2)

(3)

(4)

式中：D为电位移矢量；α为电荷密度；B为磁感应强度矢量；E为电场强度矢量；H为磁场强度矢量；J为电流密度矢量；t为时间.

假设分析域内不存在自由载荷，则式(1)和(4)可以简化为

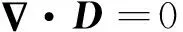
(5)

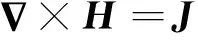
(6)

在电磁场分析中，直接求解E和H并不方便，为了降低求解难度，引入矢量磁位A和标量电位φ，分别满足：

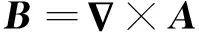
(7)

(8)

此外，B、H、J、E之间还满足以下关系：

J=Je+Js=σE+Js

(9)

B=μH=μ0μrH

(10)

式中：Je为感应电流密度；Js为激励源电流密度；σ为电导率；μ为磁导率；μ0为真空磁导率；μr为相对磁导率.

假设源电流随时间按正弦规律变化，将式(7)～(10)代入式(6)，整理得到电磁场的控制方程：

(11)

1.2 温度场模型

方管温度场的变化遵循热力学第一定律，热传导过程遵循傅里叶定律[14]：

(12)

式中：ρ为密度；c为比热容；T为温度；k为导热系数；Q为加热功率密度.

将Je和σ代入得：

(13)

同时考虑热对流和热辐射两种传热方式，方管内外表面温度边界条件如下所示：

(14)

式中：n为边界面法向量；h为表面对流换热系数；Tamb为环境温度；ε为表面发射率；σsb为斯特藩-玻尔兹曼常量.

2 几何模型及边界条件

方管局部感应加热的三维模型如图1(a)所示.方管的圆角外侧排布着平行于z轴方向的同一根铜管，铜管外侧安装有导磁体.为了保证加热段铜管的平行度，铜管两端分别加装固定板.铜管、导磁体和固定板一同构成加热线圈的主体.

为了提高求解效率，对三维模型进行简化，将图1(a)中所标横截面的二维模型作为研究对象建模，将方管形心设为平面直角坐标系的原点，如图1(b)所示.

为了更加贴近实际状况下的磁感线分布状态，在模型的最外围边界上施加磁感线平行边界条件：

A=0

(15)

电磁场在其他内部边界上具有连续性，涡流区和非涡流区交界面的边界条件[15]为

n×(H1-H2)=0

(16)

式中：H1和H2分别为涡流区和非涡流区的磁场强度矢量.

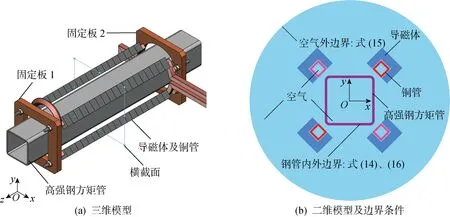
图1 几何模型Fig.1 Geometric model

3 数值模拟

数值模拟过程可分为3个部分：前处理、求解以及后处理.本文基于ANSYS参数化设计语言(ANSYS Parametric Design Language, APDL)，实现了全流程的参数化设计与分析.

3.1 前处理

首先在绘图软件中绘制二维模型，导出为通用图形文件，然后导入到ANSYS中生成几何模型.之后，定义单元类型和材料参数并指定给相应几何面，设置网格密度并完成网格划分，如图2所示.可以看出，空气域的网格形状不规则且尺寸最大.方管、铜管和导磁体的网格均由规则四边形构成，且网格细小，过渡均匀.从内圆角到外圆角，方管网格的径向厚度逐渐减小，外圆角表层的网格厚度最小，设为室温下集肤深度的一半，这样可以充分模拟出感应加热的集肤效应.最后选择相应边界，分别施加电磁场和温度场边界条件.前处理中所有点、线和面的选择以及数值设定都基于APDL命令流，这样可以大幅降低改变几何模型或者载荷参数后的工作量.

为保证计算结果准确性，所有物理量都采用国际单位制.方管横截面宽度和高度均为0.04 m，厚度为0.002 m，内、外圆角半径分别为0.002 m和0.004 m.在电磁场分析中，铜管、方管、导磁体和空气域均选用基于矢量磁位理论的二维八节点磁单元PLANE53.而在温度场分析中，由于只研究方管的温度变化，所以只需将方管单元定义为二维八节点热单元PLANE77，其他区域无需定义热单元.

定义铜管、空气域和导磁体的相对磁导率μr分别为1、1及 1 000，由于三者不参与温度场计算，所以无需额外定义温度场相关的材料参数.方管参与电磁场和温度场的耦合计算，需要定义随温度变化的相对磁导率μr、电阻率ρT、导热系数k和比热容c等材料参数[16]，如表1所示.

前处理主要常数如表2所示，其中环境温度Tamb设为室温293 K.方管表面与周围空气的对流换热系数h[17]选用40 W·m-2·K-1.于坤等[18]的研究成果表明，当温度超过900 ℃以后，ε趋于0.7，所以本文选用ε为0.68.

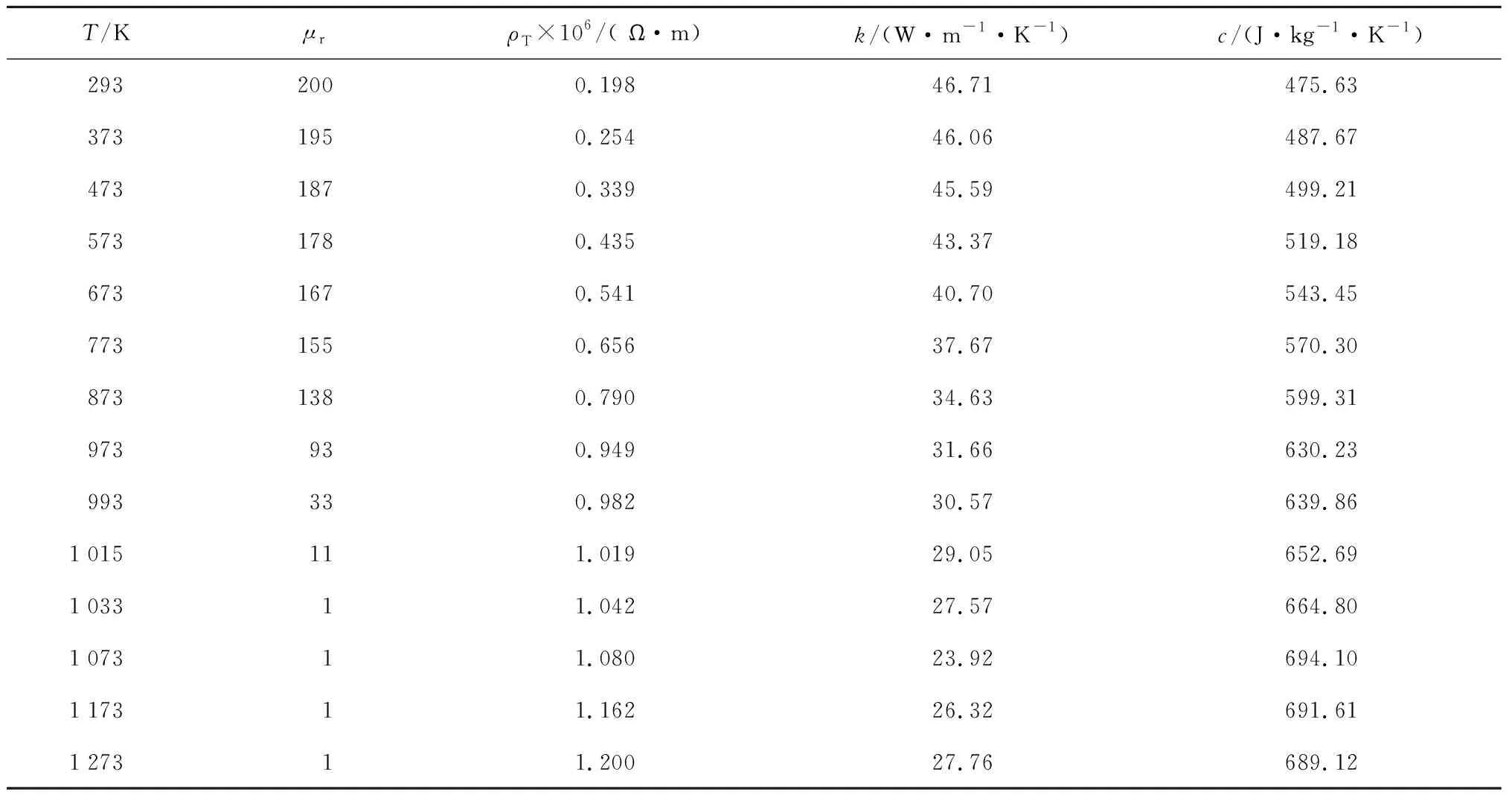
表1 高强度钢材料参数Tab.1 Material parameters of high strength steel

3.2 求解流程

感应加热技术是一种建立在电磁感应和电流热效应两个物理原理基础上的电加热方法，因此感应加热数值模拟涉及到电磁场和温度场的耦合分析，本文选用物理环境法实现它们的顺序耦合.此方法使用同一个满足所有物理场要求的实体模型和网格，然后创建多个用来定义物理环境的物理文件，基于APDL命令流，反复调用不同文件，实现载荷在多物理场中的传递，计算流程如图3所示.其中，Δt为时间步增量，n为预设步数.

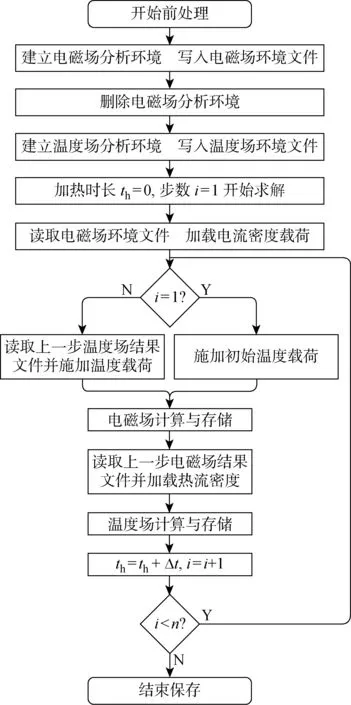
图3 电磁-温度顺序耦合计算流程Fig.3 Electromagnetic-temperature sequential coupling calculation process

首先分别在电磁场和温度场环境中完成相应的设置，并写入到不同的物理环境文件中.下一步基于APDL命令流，先调用电磁场环境文件，施加初始温度载荷，完成第一次电磁场的求解，保存结果到电磁场结果文件中.之后读取该结果文件，将感应电流生成的焦耳热作为内热源加载到温度场中，完成温度场的求解并保存，根据求解后的实时温度，对材料参数进行更新.最后根据时间步增量Δt更新加热时长th，同时分析步数i增加，进入下一个分析步的求解.整个过程循环往复，直到分析步数i增加到与预设步数n相等时，循环结束，求解完毕.

3.3 模拟参数

在局部感应加热过程中，铜管和方管之间的加热间距、铜管横截面尺寸及长度、导磁体的选用、加热频率、加热功率及加热时长是7个主要的模拟参数.理论上，铜管和方管之间的加热间距越小，加热效率越高，但是两者也更容易接触，造成短路.综合考虑加热效率和安全性，铜管外表面和方管外圆角最短距离定为0.004 m.根据方管圆角区域的几何尺寸和加热间距，选用的铜管横截面宽度和高度均为0.01 m，厚度为 0.001 5 m.铜管长度较短时，对加热功率的要求较大，会造成不必要的设备成本增加，而铜管过长时，由于铜管自重及加工制作难度，铜管的平面度和平行度会有所下降，综合考量后，加热段铜管长度选用0.1 m.

除了上述3个标量参数，将剩余4个参数作为变量参数考虑，为了研究导磁体的影响，分别建立含导磁体模型和无导磁体模型，考虑到实际黏结状态，将导磁体与铜管的间隙值设为 0.000 5 m.根据方管厚度值0.002 m和加热温度峰值 1 100 ℃，加热频率范围选取1～100 kHz，加热功率范围选用 30～55 kW.通过加热功率换算得到电流值，再将电流值除以铜管截面积，得到加载在铜管上的电流密度.考虑到实际电流的走向与图1(a)中的z轴平行，规定一、三象限铜管上的电流密度为正值，二、四象限铜管上的电流密度为负值，由于整个电路串联，所以各象限电流密度的绝对值相等.加热时长为加热段铜管长度和方管移动速度之比，由于加热段铜管长度已定为0.1 m，所以当方管移动速度范围选用0.5～6 m·min-1时，相应得到加热时长的范围为1～12 s.

将有限元模型求解之后的结果分别存储在电磁场结果文件和温度场结果文件中，分别读入两个文件，从某一时刻云图结果、随路径或时间变化的节点结果等方面进行讨论与分析.

4 结果与讨论

4.1 导磁体的效果

加热频率为80 kHz，加热功率为30 kW，加热时长为1 s时的磁感线分布如图4所示，其中图4(a)和图4(b)分别为无导磁体模型和含导磁体模型的整体结果图以及第一象限结果图.由图4(a)可以看出，在铜管外表面区域，磁感线最为密集，而距离铜管中心越远，磁感线越稀疏.但由于方管的存在，原本呈圆形分布的磁感线被迫经过外圆角表层，从而增大了表面磁感线密度.由图4(b)可以看出，在导磁体的作用下，磁感线分布区域大幅缩小，尤其是在导磁体外侧空气域中，几乎不存在磁感线.与此同时，由于大量磁感线从导磁体内穿过，所以方管外圆角表层的磁感线密度大幅上升.

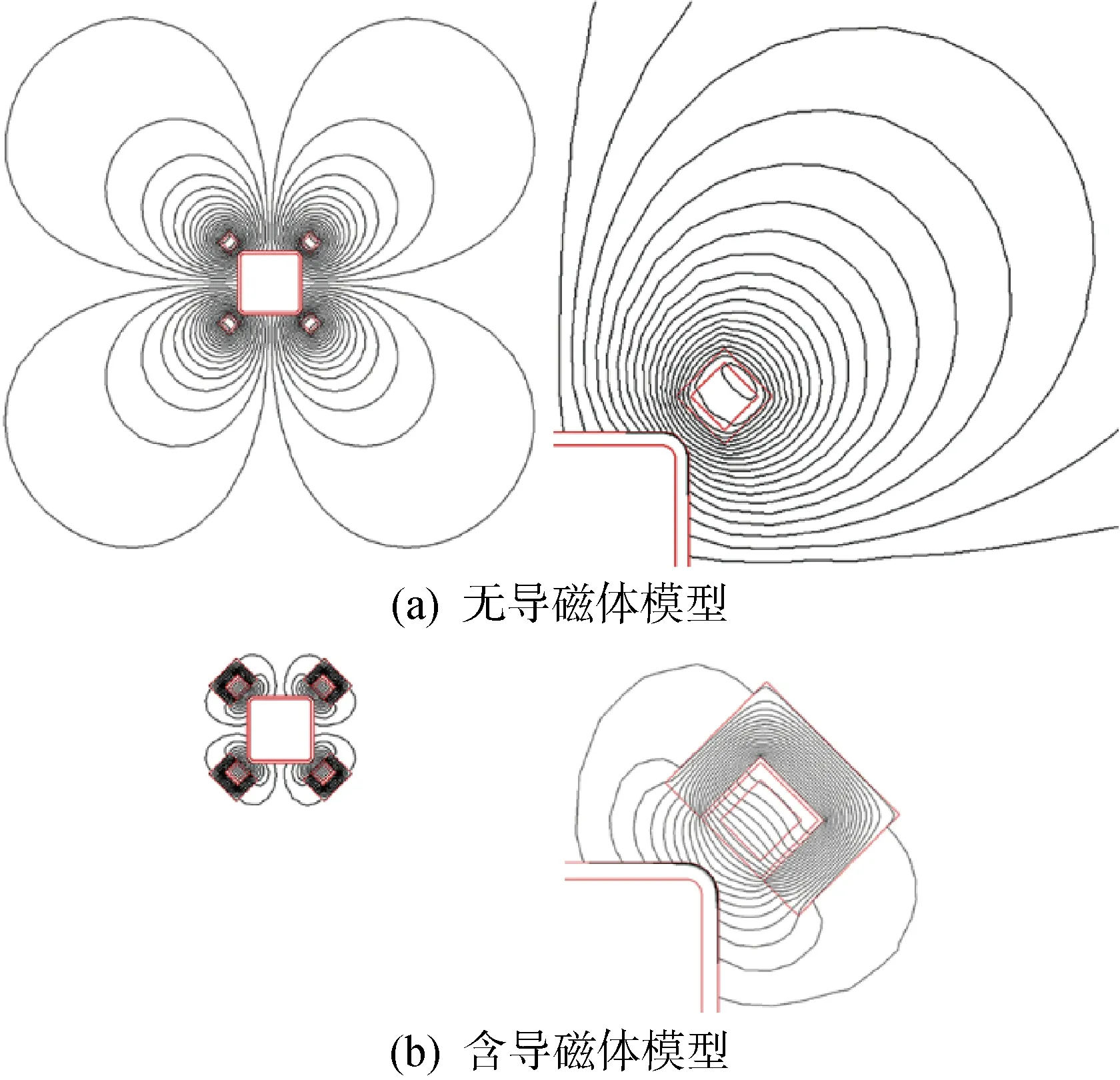
图4 导磁体对磁感线的影响Fig.4 Influence of magnetizers on magnetic induction line

导磁体的相对磁导率远高于空气、铜管和方管，强烈降低了所处区域的磁阻，可以将原本自由散布在空气域中的磁感线“吸引”到体内，使磁感线从体内穿过，大幅提升体内磁通量，然后通过控制开口位置，将体内高密度磁感线引导至待加热区域.在其他模拟参数相同的情况下，可以明显看出导磁体对空间磁感线分布的控制能力以及对局部区域磁通量的大幅提升效果.

与图4相同的加热参数下的磁场强度(H)结果如图5所示.由图5(a)可以看出，与磁感线分布规律相同，磁场强度在与方管圆角相邻的铜管外壁附近达到了最大值，约为 27 990 A/m，磁场强度沿铜管外表面向外逐渐递减.而在图5(b)中，磁场强度最大值出现在相似位置，约为 239 700 A/m，大于图5(a)中磁场强度极值的8.5倍.可以看出，在导磁体开口位置与方管圆角之间，营造出了强磁场区域，而在导磁体的另外3个方向，磁场强度迅速衰减，接近0.

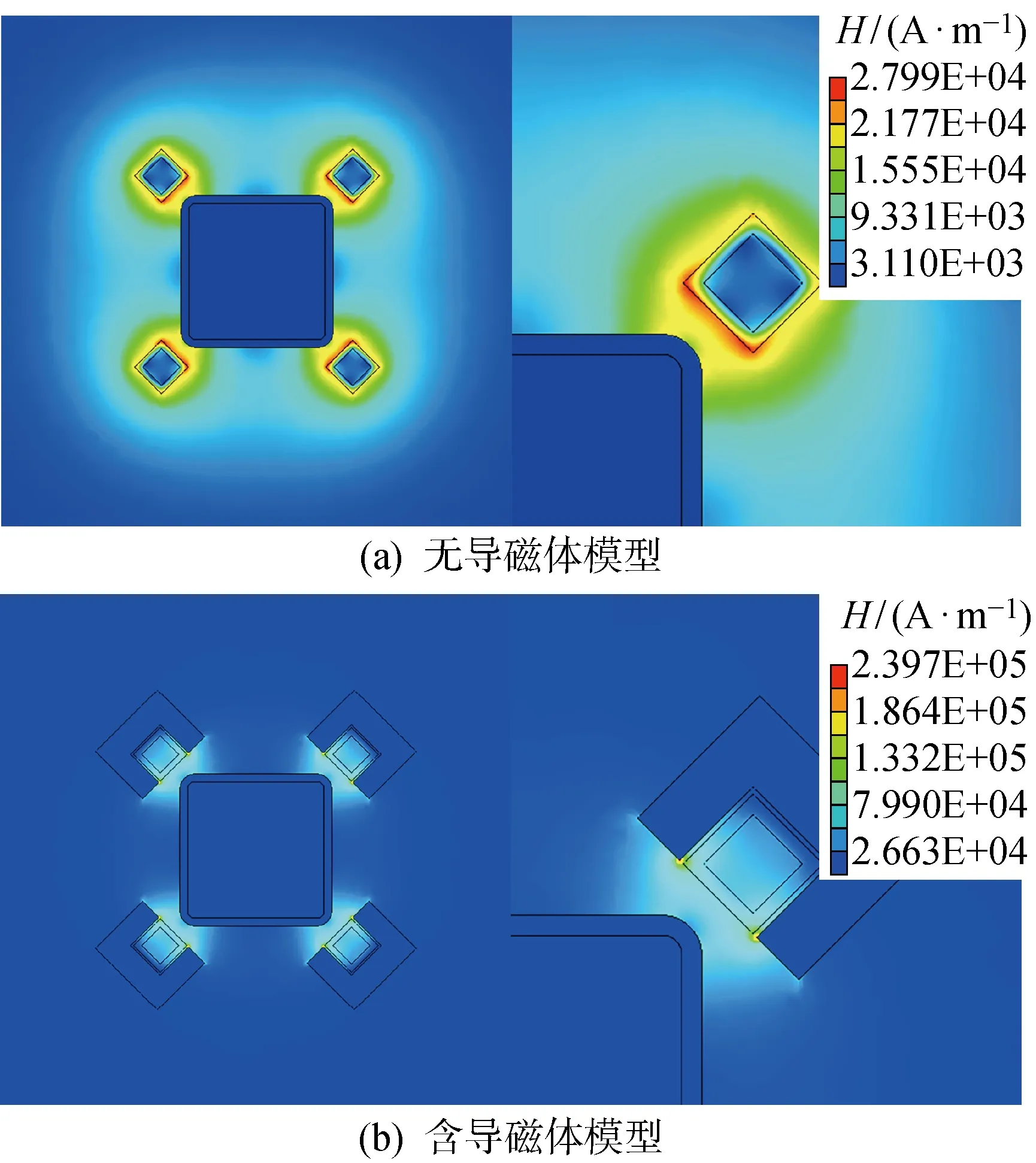
图5 导磁体对磁场强度的影响Fig.5 Influence of magnetizers on magnetic field intensity

无导磁体模型的加热温度峰值仅为91.7 ℃，而含导磁体模型则达到了350.2 ℃，约是前者的4倍.导磁体将原本发散的磁场集中到方管外圆角区域，使该区域的磁场强度提高近一个量级，这是导磁体能够大幅提升加热效率的根本原因.

4.2 加热频率的影响

为研究加热频率(f)对模拟结果的影响，采用含导磁体模型，选用物理环境法，加热时长选用1 s，加热功率选用P=30 kW，对f=1，80 kHz 分别建模分析.图6所示为两种加热频率下圆角区域加热温度和磁感应强度(B)分布情况.可以看出，当f=1 kHz时，图6(a)中方管圆角温度分布较为均匀，最大值位于外圆角表层中心，约为20.23 ℃，相比较环境温度20 ℃，升温幅度极小.当f=80 kHz时，图6(b)中温度最大值仍在同一位置，约为 354.6 ℃，但无论是径向还是周向，温度差值都明显增大，内外圆角中心位置温差约为100 ℃.

图6 加热频率对加热温度和磁感应强度的影响Fig.6 Influence of heating frequency on heating temperature and magnetic flux density

由式(13)可知，感应电流密度Je直接决定加热功率密度Q的值，而感应电流密度Je的值和分布规律又与磁感应强度B保持一致.当f=1 kHz时，如图6(c)所示，方管圆角区域的磁感应强度分布范围较广，覆盖了从外圆角表层到约1/2板厚的区域，表层磁感应强度最大，约为1.543 T.当f=80 kHz 时，图6(d)中方管圆角区域的磁感应强度分布范围很窄，集中在从外圆角表层到约1/10板厚的区域，与此同时，表层磁感应强度峰值约为5.861 T.通过对比可知，当f从 1 kHz 提升到 80 kHz 时，磁感应强度覆盖区域减少了80%，表层磁感应强度提升到近4倍，这使得表层温度提升了约16倍.

当加热频率较低时，磁感应强度在较大区域内均匀分布，整个区域缓慢升温，而当加热频率增加后，磁感应强度大幅提高并集中在外圆角表层区域，加热速度和温度大幅提升，但同时会增大外圆角和内圆角之间的温差.由此可见，存在最佳加热频率，可以在适当的加热速度下，实现圆角区域均匀透热的加热要求.

为了找到最佳加热频率，在其他参数不变的情况下，额外进行20、40及60 kHz共3种加热频率下的数值模拟，从外圆角中心点到内圆角中心点路径的磁感应强度分布如图7所示，图中d为外圆角中心点沿径向的深度.可以看出，不同频率下的磁感应强度都呈现出先增长至峰值，再衰减至0的趋势.磁感应强度峰值与加热频率成正比，而峰值所处深度以及归零深度则与加热频率成反比.f=1 kHz时，磁感应强度峰值在约0.15 mm深度出现，并且在约 1.2 mm 深度(1/2板厚附近)趋于0，这与图6(c)的结果完全吻合.对于其他4种加热频率，峰值所处深度均小于0.04 mm，磁感应强度在0.3 mm深度之内基本都已归零.

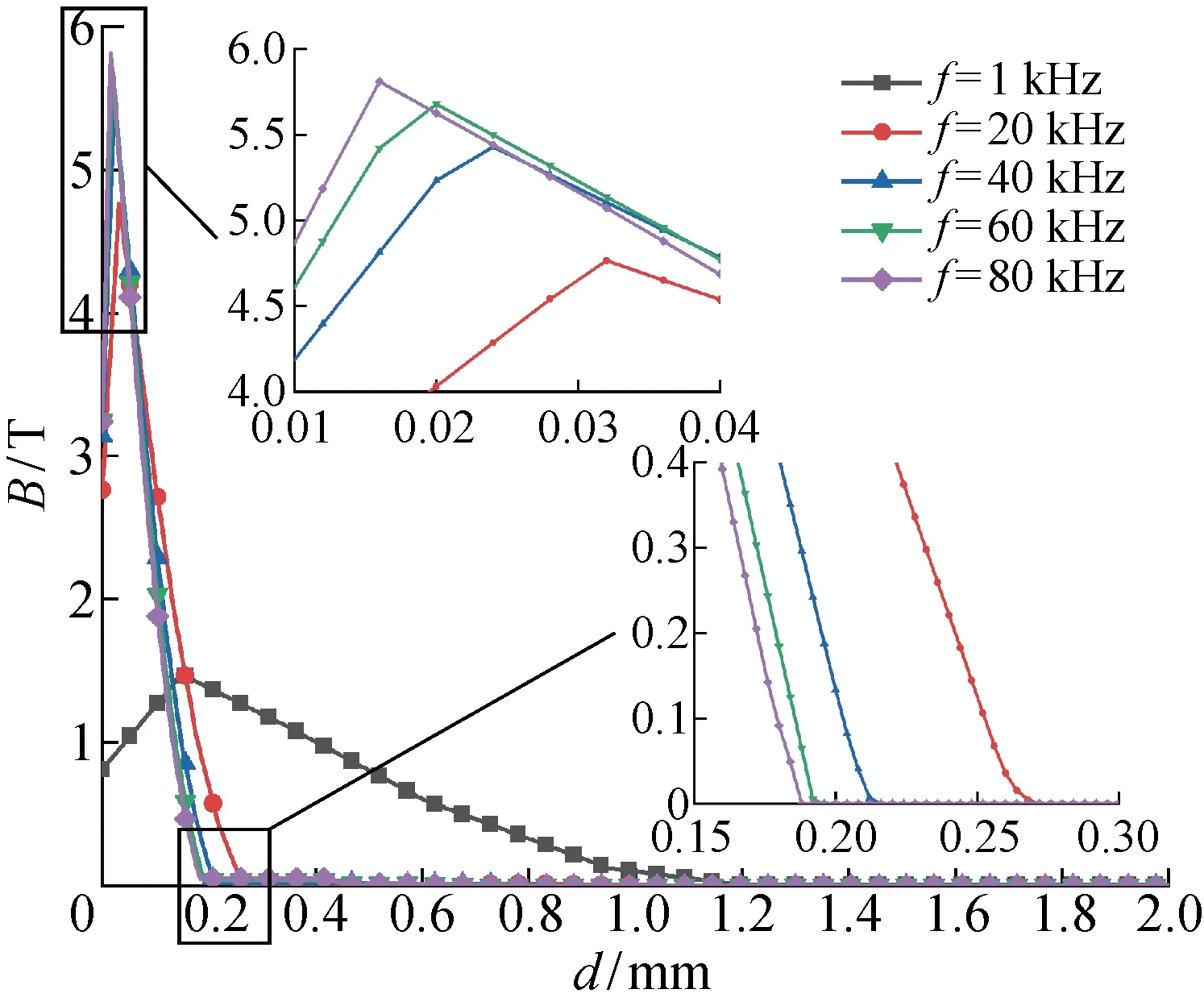
图7 磁感应强度随加热频率的变化Fig.7 Magnetic flux density versus heating frequency

图6和7表明，随着加热频率提升，磁感应强度峰值所处深度和归零深度均向外圆角表层移动.当加热频率较高时，磁感应强度在距离表层不到1/10厚度的区域内，迅速增长至峰值并急速衰减至0，表明磁感应强度具有与感应电流相似的集肤效应.这决定了工件表层最先被加热，直到表层温度超过居里点后，表层失磁，加热位置才开始向深层移动，导致表层和深层之间存在从高温到低温的温度梯度.圆角区域均匀透热的实质是要保证内圆角区域达到目标加热温度的同时，尽量缩小外圆角表层峰值温度与目标加热温度的温度差值.

高强度钢方管材质为亚共析钢，通过JMatPro软件计算得到，在平衡状态下的奥氏体和铁素体共存的最高温度约为840 ℃，考虑到感应加热过程温升速度较快，所以把目标加热温度提高至900 ℃，让铁素体尽可能多地转变为奥氏体.为了满足厚度方向均匀透热的加热要求，当加热功率为50 kW，内圆角中心位置达到900 ℃时，对不同加热频率所需加热时长以及外圆角和内圆角中心位置的温度差值(ΔT)进行统计，计算相邻两数据点之间的增长率，结果如图8所示.

图8 加热时长和温度差值随加热频率的变化Fig.8 Heating time and temperature difference versus heating frequency

从图中可以看出，随着加热频率的增加，加热时长逐步降低，温度差值不断增大.当f从20 kHz增加到40 kHz时，加热时长减少了68%，温度差值增加了150%，而当f超过40 kHz以后，加热时长的降低率和温度差值的增长率都逐步减小.这是因为圆角区域几何尺寸和材料性能参数的限制，当f超过40 kHz以后，不管是磁感应强度峰值、峰值出现位置还是归零位置，差距都明显缩小(见图7).

当f=40 kHz，P=50 kW时，内圆角中心在t>2.6 s后到达900 ℃，此时内外圆角温度差值约为66 ℃.不足3 s的加热时长和小于70 ℃的温度差值可以满足加热要求，而当加热频率进一步增加时，加热时长下降的优势已经无法弥补设备成本以及温度差值提升带来的劣势.综上所述，最佳加热频率选取为40 kHz，同时为了方便计算，将加热时长 2.6 s 取整为3 s，对应的钢管移动速度为2 m/min.

4.3 加热功率的影响

在图8结果基础上，选定加热频率及时长分别为40 kHz及3 s，对47.5、50.0、52.5及55.0 kW共4种加热功率下的电磁-温度场进行数值模拟，将温度大于等于900 ℃的区域着色显示，结果如图9所示.可以看出，当其他参数相同时，加热功率越大，高温区域和温度峰值也越大.

当加热功率为47.5和50.0 kW时，如图9(a)和9(b)所示，只有部分圆角区域温度达到了 900 ℃ 以上.当加热功率为52.5 kW时，如图9(c)所示，整个圆角区域温度刚好达到900 ℃以上，温度峰值约为 1 117 ℃，加热效果比较理想.而当加热功率提升到55.0 kW时，如图9(d)所示，900 ℃以上的温度区域远超圆角区域，此时的温度峰值位于外圆角中心，约为 1 197 ℃，外圆角区域容易出现组织过热，甚至有过烧和熔化的风险.综上所述，加热功率应优先选用52.5 kW.

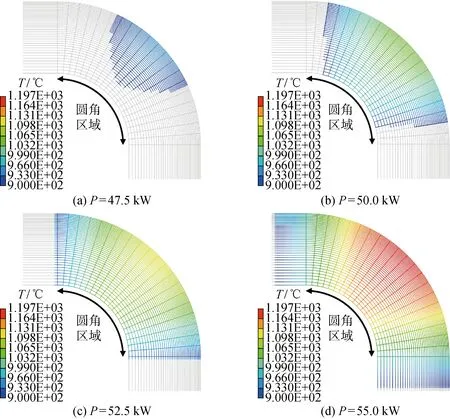
图9 圆角区域温度分布随加热功率的变化Fig.9 Temperature distribution at fillet area versus heating power

5 实验研究

5.1 加热温度

为了验证数值模拟结果的准确性，按照图1几何模型制作加热线圈，使用和有限元模型相同的标量参数以及优化后的变量参数，开展高强度钢方管局部感应加热辊压成形实验研究.其中，优化后的变量参数如下：在铜管外安装相同尺寸的导磁体；选用加热频率为40 kHz、最大输出功率为120 kW的超音频感应加热设备；钢管移动速度为2 m/min，对应加热时长为3 s；加热功率优选52.5 kW，另外两组对照实验的加热功率分别为42.5和47.5 kW.实验过程中，借助红外热像仪测量方管外表面加热温度，热像仪与方管之间的测量距离约为0.5 m.

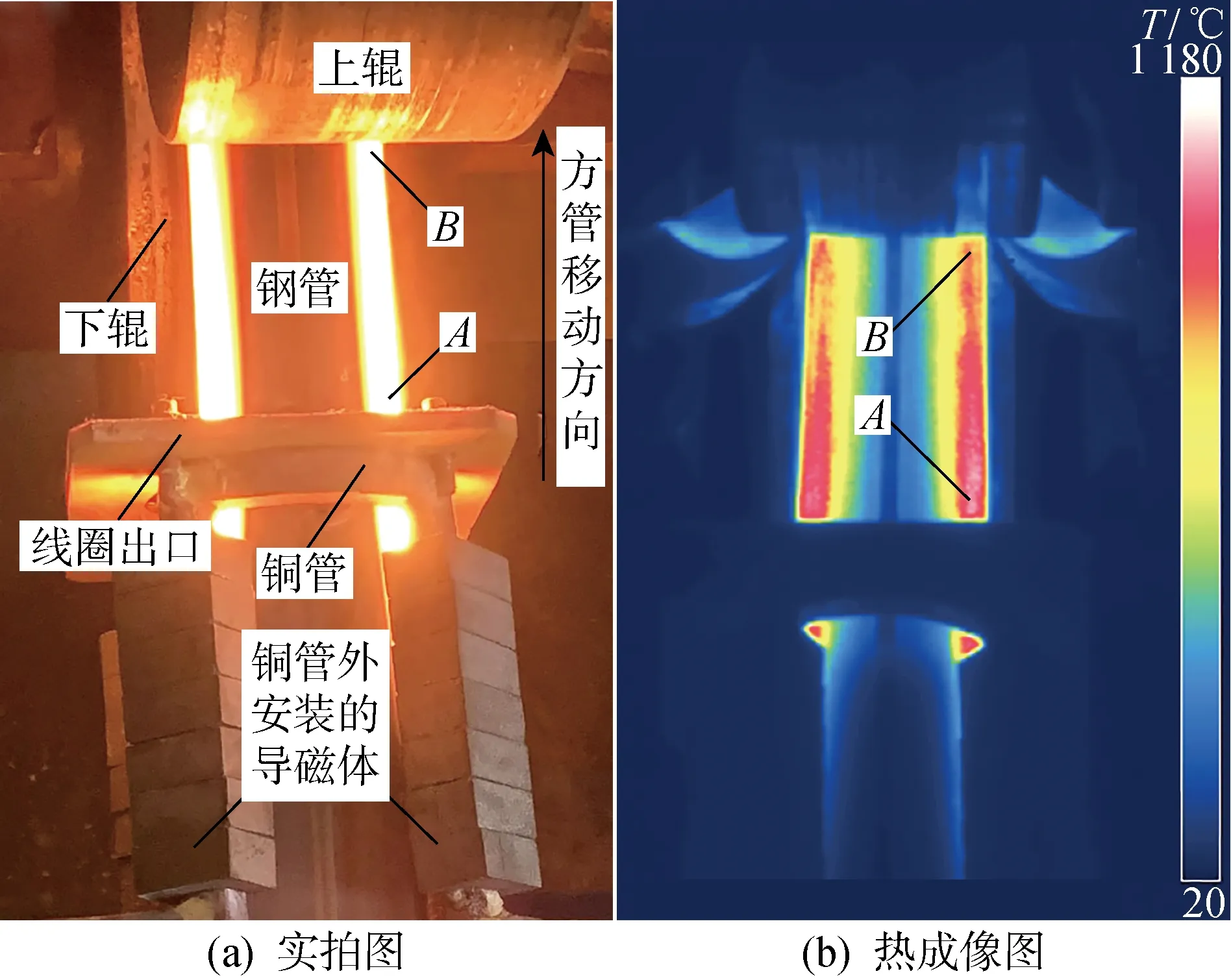
图10 局部感应加热实验Fig.10 Local induction heating experiment

当加热功率为52.5 kW时，局部感应加热实验的实拍图和热成像图如图10所示.方管自下而上移动，穿过线圈之后，进入成形道次.由于铜管和导磁体的遮挡，无法直接测量加热段的温度分布，只能通过测量空冷段的温度分布，验证数值模拟结果的准确度.在专业后处理软件中，选用与表2中一致的发射率，提取右侧外圆角中心从刚离开线圈到即将进入成形道次之间(A点与B点之间区域)的温度分布曲线.

基于APDL命令流，采用含导磁体模型和物理环境法，f=40 kHz，进行P=42.5，47.5，52.5 kW的局部感应加热数值模拟.根据方管移动距离和速度之比，得到分析时长为4.5 s，其中加热时长为3 s(从进入到离开线圈所需时间)，空冷时长为1.5 s，略大于从A点移动到B点所需时间.提取第一象限外圆角中心温度随时间变化的曲线，结合方管移动速度，将时间换算成实际位移，即可获得方管外圆角中心温度在加热段和空冷段的变化曲线.

热像仪测温结果和数值模拟结果如图11所示，其中D为电位移.在加热段初期，即加热温度低于居里点(约770 ℃)之前，温升速度较快，且与加热功率成正比.当加热温度达到居里点附近时，由于方管的相对磁导率、比热容及热导率发生剧烈变化，致使温升速度陡然上升.当加热温度超过约900 ℃后，由于方管外圆角早已失磁，此时温度上升的热量来源为深层加热位置的热传导，所以温升速度大幅下降.在空冷段，方管外圆角的热传递方式主要为与空气的热辐射和热对流以及与圆角深层位置的热传导，温降速度与幅度均与加热功率成正比.

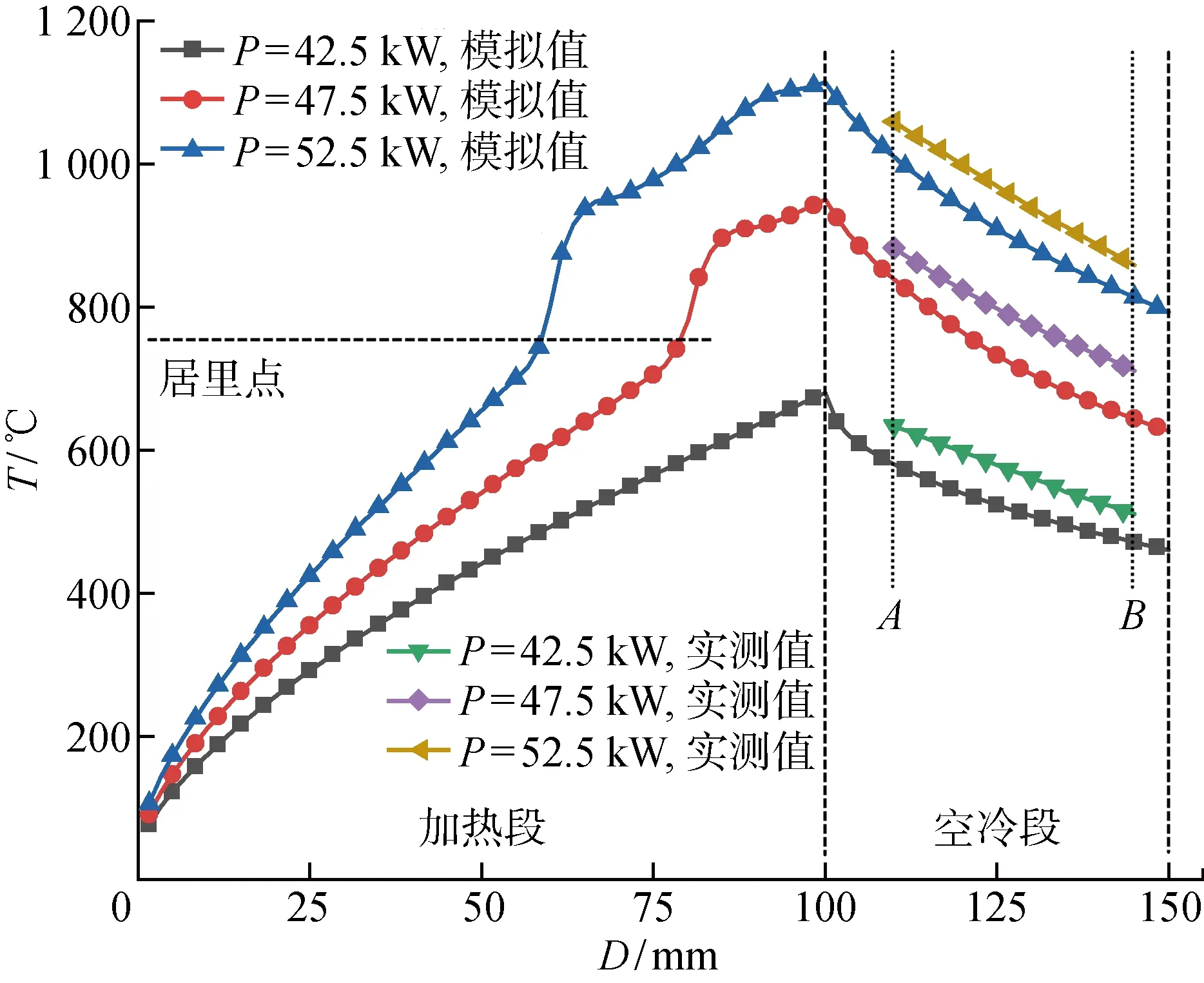
图11 温度实测值与模拟值的对比Fig.11 Comparison of measured and simulated temperature

在3种加热功率下，A点和B点之间的加热温度模拟值均低于实测值.然而根据实测值曲线的变化不难发现，在加热段和空冷段的分界处，即D为100 mm时，实测值与模拟值的准确度有所提升.这是因为方管外圆角在空冷段，只有热量的流失，材料热物性参数的取值对温度变化起到决定性作用，比如模型中采用恒定的表面换热系数，而实际状况下，它应当跟随温度差值的变化而改变.

当加热功率为42.5、47.5 及52.5 kW时，20个数据点的误差均值分别为8.95%、8.02%及5.74%，说明方管的材料热物性参数更加适用于高温场合.3种加热功率下，温度模拟值与实测值的误差均值约为7.57%，说明有限元模型具备一定的预测能力，与实际情况吻合良好.

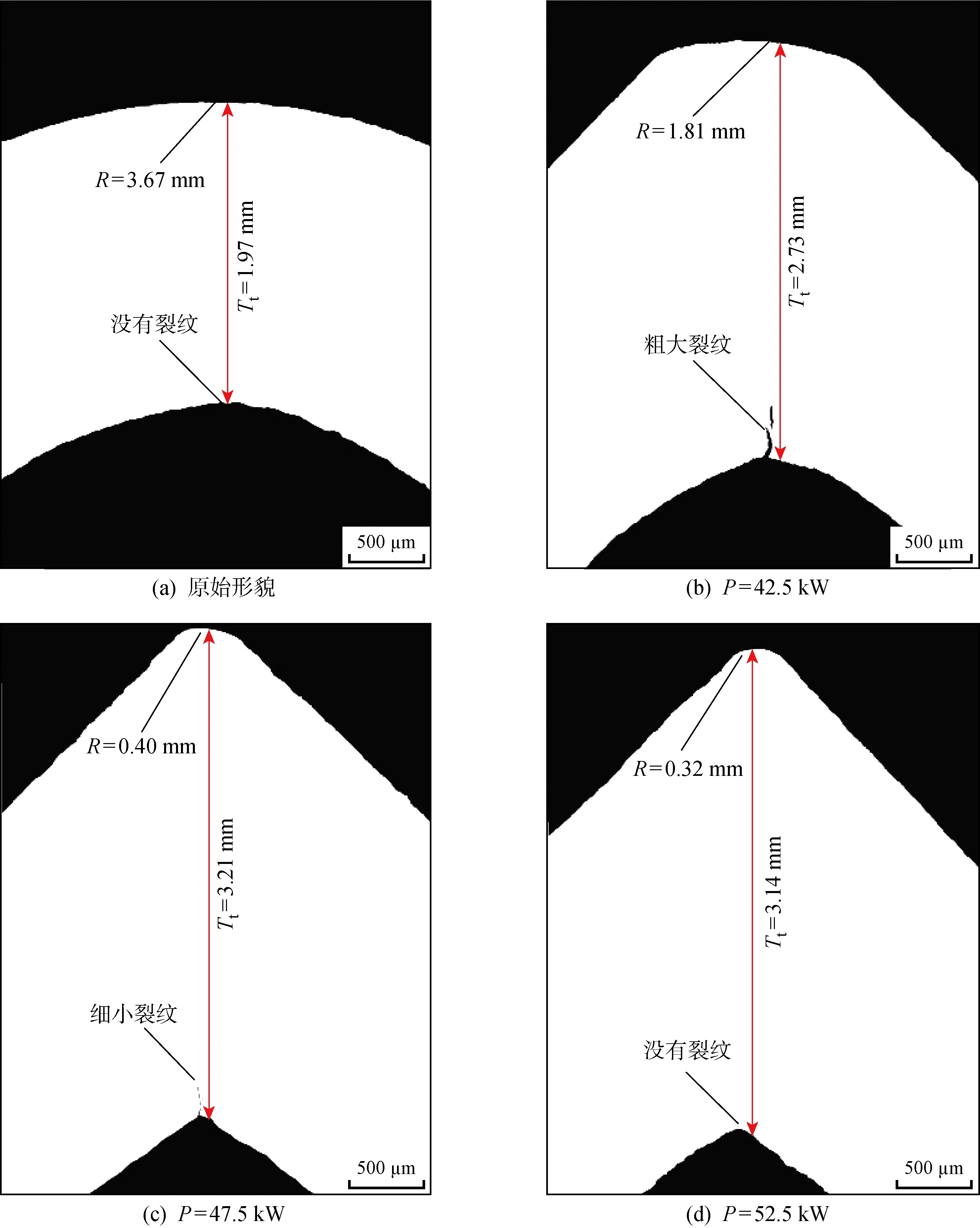
图12 角部区域形貌随加热功率的变化Fig.12 Morphology at fillet area versus heating power

5.2 角部区域形貌

对普通方管和3种加热功率下成形后的尖角方管角部区域分别取样，经过镶嵌—粗磨—细磨—抛光后，在金相显微镜下观察形貌，如图12所示.其中图12(a)为普通方管的原始角部区域形貌，图12(b)～12(d)分别为P=42.5，47.5，52.5 kW成形后的尖角方管角部区域形貌.如图12(a)所示，普通方管的角部区域厚度Tt最小，为1.97 mm，外圆角半径R最大，为3.67 mm，整个区域没有裂纹.当P=42.5 kW时，如图12(b)所示，R值减小到 1.81 mm，Tt增加到2.73 mm，但是内圆角位置出现了0.34 mm长的粗大裂纹.当P=47.5 kW时，如图12(c)所示，R减小到0.40 mm，Tt增加到 3.21 mm，但是内圆角位置仍有0.18 mm长的细小裂纹.当P=52.5 kW时，如图12(d)所示，R继续减小到0.32 mm，Tt为3.14 mm，未出现任何裂纹.

普通方管角部区域经过多道次冷弯成形，从平直板带逐渐弯曲成圆角，不可避免地出现弯曲减薄现象，相比较板带厚度2 mm，角部厚度降低了 0.03 mm，此时R超过板厚的1.8倍，足够大的弯曲半径确保角部区域未出现裂纹.然而，当P=42.5 kW 时，圆角形貌开始发生较大变化，Tt超过板厚，R小于板厚，但是由于加热功率不足，导致内圆角区域温度较低，成形时出现了粗大裂纹.

当P提升到47.5及52.5 kW时，Tt和R分别进一步增加和减小.参照图9(a)和图9(c)所示，当P=47.5 kW时，内圆角区域温度仍低于 900 ℃，导致成形时出现细小裂纹，而当P=52.5 kW 时，由于整个圆角区域温度均超过 900 ℃，充分提升了高强度钢塑性变形能力，与原始形貌相比，Tt增加约59%，R减小约91%；与文献[5]研究结果相比，R减小约84%，同时彻底克服内圆角裂纹缺陷，消除后续使用中的安全隐患.

6 结论

(1) 基于矢量磁位法和物理环境法，利用APDL命令流建立局部感应加热辊压成形工艺的电磁-温度场耦合模型.分析不同加热工艺参数对模拟结果的影响，并基于优化后参数进行实验研究.加热温度模拟值与实测值的误差均值约为7.57%，说明有限元模型预测能力良好，可以指导实际生产实践.

(2) 模拟结果表明，导磁体可以将原本自由散布在空间中的磁感线“吸引”到体内，再通过控制开口位置，将体内高密度磁感线引导至待加热区域，大幅提高该区域的磁场强度.在局部感应加热技术中，应当采用外形适宜的导磁体，以便提升局部感应加热效率.

(3) 模拟结果表明，磁感应强度具有与感应电流相似的集肤效应，电磁集肤效应对温度场分布起到决定性作用.需要快速均匀透热时，应当根据目标加热温度，首先选择适中的加热频率和加热时长，然后再根据目标加热范围，确定加热功率.本工艺确定的最佳加热频率、加热功率以及加热时长分别为 40 kHz、52.5 kW以及3 s.

(4) 实验结果表明，选用数值模拟优化后的加热工艺参数，加热温度符合预期，“尖角化”效果显著提升.成形后的高强度钢尖角方管外圆角半径为0.32 mm，减小约91%，角部厚度为3.14 mm，增加约59%，没有出现裂纹缺陷，满足工程应用的安全要求.