基于单位四元数矩阵实表示的坐标转换算法研究

秦 锋,鹿 松,张振虎

〔1.中国核工业集团三门核电有限公司,浙江 台州 317112;2.上海勘察设计研究院(集团)有限公司,上海 200093〕

0 引 言

空间三维坐标转换一直是测量领域的重要研究内容。目前很多坐标转换都涉及大旋转角的空间坐标转换,传统的布尔莎七参数模型只适用于小角度旋转,难以满足要求。当前关于大角度坐标转换模型算法一般有误差方程线性化算法[1-4]、罗德里格矩阵算法[5-9]、四元数法[10-14]、奇异值分解(SVD)算法等[15-16]。其中,误差方程线性化算法利用一阶微分将误差方程线性化后迭代求解,该算法存在计算复杂、迭代不收敛或收敛到非极值,以及求解过程中可能会出现矩阵奇异或矩阵条件数过大等问题。罗德里格矩阵算法利用反对称矩阵构建线性方程进行求解,根据文献[17]论证其精度略低于七参数迭代模型。奇异值分解法其数学基础为矩阵分析中子空间的旋转问题[18],该算法适用性强,但需要进行奇异值分解,难以普遍应用。四元数法利用单位四元数表示旋转,不用进行迭代,可提供平滑差值和避免万向锁问题,其用于坐标转换参数求解时,适用性强,可以用于任意角度的三维坐标转换问题求解,但四元数法理论较复杂,其乘积计算不便。本文基于单位四元数矩阵实表示的方式[19]将四元数体上的求解转化成矩阵上的求解,并给出了利用单位四元数进行坐标转化的两种算法的证明过程,公式推导简便,容易理解,经数据验证,两种算法解算结果准确一致。

1 四元数基础知识

1.1 四元数定义及性质

四元数是简单的超复数,由1个实部q0和3个虚部q1、q2、q3组成,可表示为:

(1)

式中,i、j、k满足i2=j2=k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j。其单位四元数满足:

(2)

其共轭四元数为:

(3)

四元数模定义为:

(4)

四元数模满足以下公式:

(5)

(6)

四元数的逆:

(7)

1.2 四元数运算

四元数加法如下:

(8)

四元数乘法(格拉斯曼积)如下:

(9)

从式(8)和式(9)容易验证,四元数加法满足结合律和交换律,乘法满足结合律和分配律,但不满足交换律,这导致了四元数之间运算复杂。为了简化四元数之间的运算,根据参考文献[19],借助四元数的矩阵实表示,可以将四元数域上的运算转化为实数域上向量和矩阵的运算。实数域上向量和矩阵的运算比四元数域的计算简单,且计算过程明了,便于公式推导和实际应用。

1.3 四元数的矩阵实表示

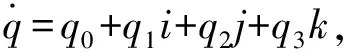
(10)

(11)

(12)

(13)

(14)

(15)

(16)

2 计算原理及公式推导

2.1 空间坐标转换模型

空间坐标转换模型可表示为:

(17)

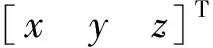
将坐标转换模型以向量形式表示:

(18)

为便于计算,将坐标进行中心化处理:

(19)

由式(18)和式(19)可以推导出平移参数计算公式:

(20)

而式(18)变为:

(21)

2.2 利用单位四元数进行坐标转换的第一种方法证明

构造如下优化函数f1:

(22)

因R为正交矩阵,故有‖Rri‖2=‖ri‖2,上式化简为:

(23)

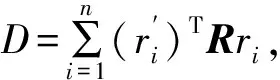
(24)

注意:上式的“·”表示四元数的点积,其结果为一个标量。

根据引理1和引理2,将式(24)采用矩阵实表示进行表示:

(25)

(26)

(27)

式(27)为关于λ的一元二次方程,尺度系数计算公式如式(28)所示。当λ取式(28)时,f1取最小值。

(28)

求得单位四元数后,可根据下式计算旋转矩阵R,再结合式(20)及式(28)可解出平移参数。

(29)

2.3 利用单位四元数进行坐标转换的第二种方法证明

将式(22)用单位四元数表示如下:

(30)

采用矩阵实表示表达四元数:

(31)

(32)

则函数f1可表示为:

(33)

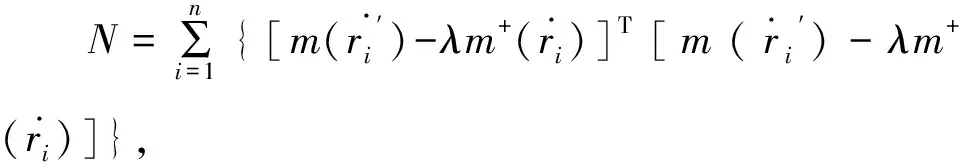
(34)

利用特征分解计算出单位四元数后,将式(30)展开,得:

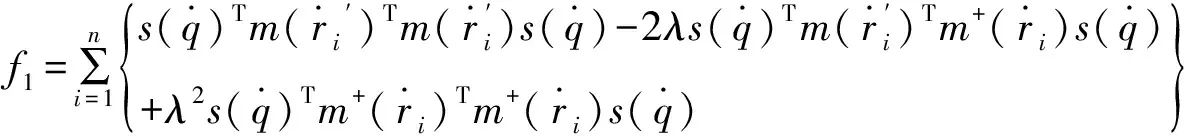
(35)

式(32)为关于λ的一元二次方程,当λ取式(33)值时,f1取最小值。

(36)

求得单位四元数后,可根据式(29)计算旋转矩阵R,再结合式(20)及式(36)可解出平移参数。

3 算例分析

算例一:

以激光跟踪仪测量的某6个公共点转站前和转站后的空间三维坐标为例,公共点坐标如表1所示,采用本文两种算法计算坐标转换单位四元数、尺度系数和平移参数,并将四元数转化为旋转矩阵。另采用奇异值分解法(SVD)计算结果作为对比。

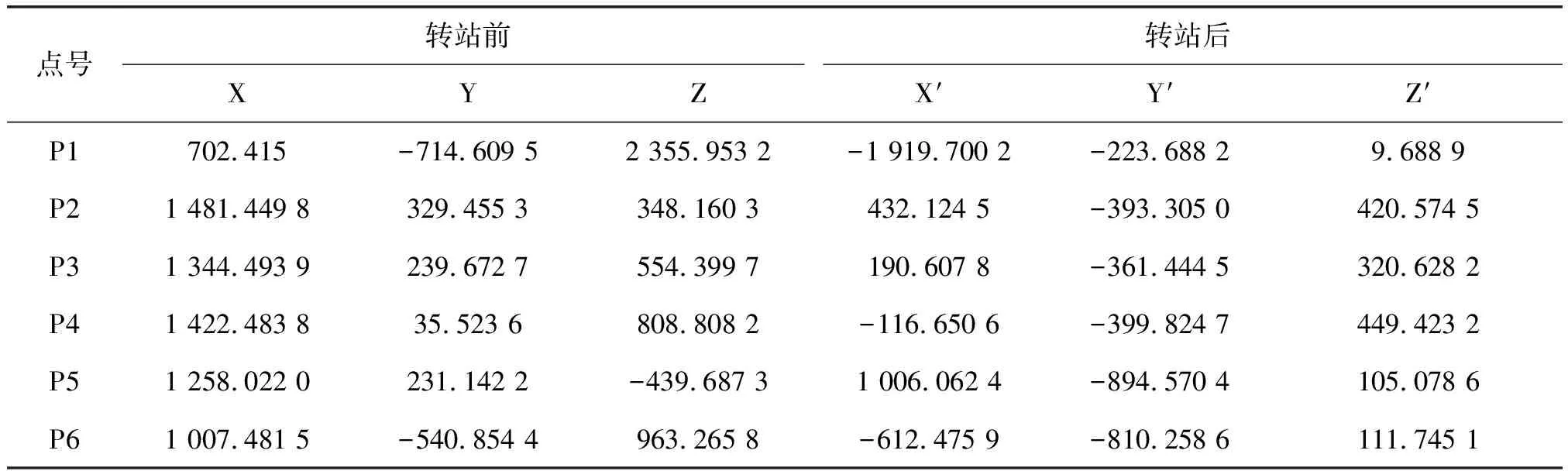
表1 激光跟踪仪转站前后公共点测量数据(单位/mm)

在对数据进行中心化处理后,采用本文第一种算法得到的特征分解矩阵M、特征向量矩阵U1、特征值矩阵V1如式(37)-(39)所示。

(37)

(38)

(39)

从上式可以看出,V1中最大特征值对应U1中的第四列特征向量,即为所求单位四元数。

本文第二种计算方法先假定尺度系数λ为1,在对数据进行中心化处理后,可计算得到特征分解矩阵N、特征向量矩阵U2及特征值矩阵V2。V2中最小特征值对应U2中的特征向量即为所求单位四元数。因篇幅所限,不再一一展示矩阵N、U2及V2。

本文两种方法所求的单位四元数、尺度系数、平移参数如表2所示。两种方法计算的单位四元数符号相反,但其绝对值一致,不影响旋转矩阵的计算;尺度系数和平移参数完全一致,说明本文两种方法是一致的。

表2 本文两种算法计算的坐标转换参数

为便于与奇异值分解算法(SVD)计算结果进行对比,采用表2中计算得到的四元数,根据公式(29)计算本文两种方法得到的旋转矩阵。因本文两种方法得到的旋转矩阵一致,故只展示第一种方法计算得到的旋转矩阵R。

(40)

奇异值分解算法(SVD)计算出的旋转矩阵、尺度系数及平移参数如表3所示。

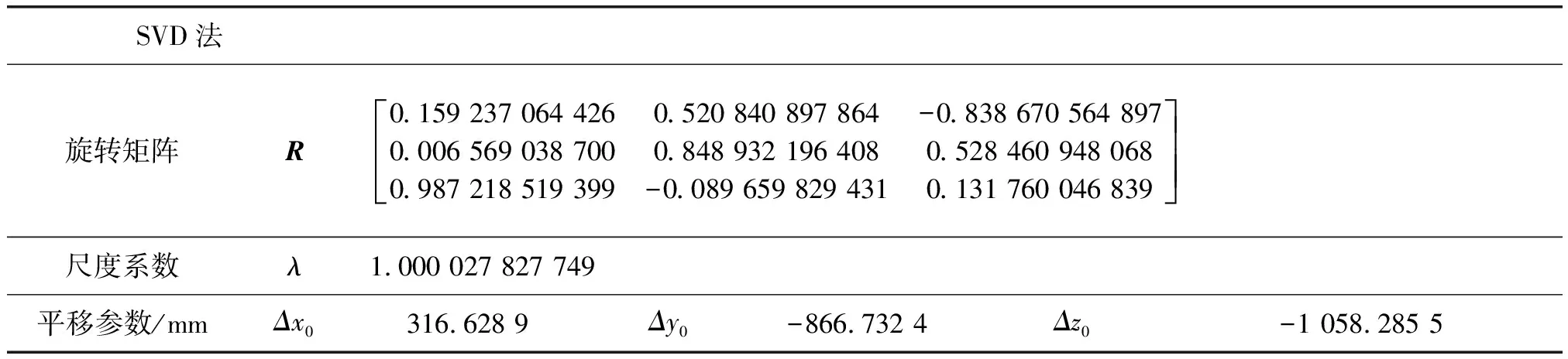
表3 奇异值分解算法(SVD)计算的坐标转换参数

对比表2和表3可以看出,本文算法和SVD法计算的结果高度一致,说明本文算法是正确的。

算例二:

以文献[3]中算例为例,计算坐标转换参数。首先将文献[3]中设计坐标系转换成左手系,与测量坐标系一致;根据本文两种算法,计算单位四元数、尺度系数、平移参数及旋转矩阵。因本文两种算法计算结果完全一致,故只展示第一种算法计算结果。计算结果如表4所示。

表4 文献[3]算例本文算法计算结果

本文算法与文献[3]和文献[4]计算的坐标较差数据如表5所示,可发现本文算法与文献[4]的坐标较差数据完全一致。

表5 坐标较差数据(单位/mm)

4 结 语

本文基于单位四元数矩阵实表示的方式推导并证明了利用单位四元数进行空间三维坐标转换的两种算法,两种算法论证过程清晰,适用性强,不用进行迭代,方便编程,适合大角度的空间坐标转换。