负三角形变位型下剥离气球模的非线性演化特征*

秦晨晨 牟茂淋† 陈少永

1) (四川大学物理学院,成都 610065)

2) (四川大学,高能量密度物理国家重点实验室,成都 610065)

托卡马克实验中已经实现了负三角形变位型下的高约束放电,其特点是具有较低的台基,并伴随幅值较小且频率较高的边界局域模.本文基于不同三角形变的托卡马克平衡,研究了负三角形变位型条件下剥离气球模的非线性演化特征.研究发现,由于弱场侧坏曲率区域增大,负三角形变位型会使剥离气球模失稳;在非线性阶段,负三角形变位型下的剥离气球模压强扰动分布在极向截面上扩展到了弱场侧的顶部和底部区域,使得边界局域模更早发生崩塌,同时,在负三角形变位型下,多种环向模数的扰动被激发并增长,故而具有更明显的湍流输运特性.

1 引言

高约束运行模式(high confinement regime,H 模)[1]因其较高的约束参数已成为未来聚变堆稳态运行的基本模式之一,但高约束条件下伴随的Ⅰ型边界局域模(edge localized mode,ELM)[2]会引起等离子体边缘区域台基的周期性崩塌,崩塌过程中释放的强粒子流和热流会导致偏滤器热负荷过载.ELM 现象通常被认为由剥离气球模(peelingballooning mode,P-B 模)[3]激发产生,该不稳定性由H 模放电时台基区电流驱动的剥离模和压强梯度驱动的气球模耦合而成.

三角形变是等离子体形状参数之一,在DIII-D[4],JET[5],ASDEX Upgrade[6]及其他托卡马克装置[7]上的H 模放电实验发现,正三角形变(positive triangularity,PT)位型放电时约束水平显著提高.相关模拟表明,PT 可以解耦P-B 模,使台基获得更大压强梯度和电流,从而有助于进入气球模第二稳定区[3,8].然而,在实验和模拟中,负三角形变(negative triangularity,NT)位型具有截然不同的特性[9].一方面,NT 可以增加低约束模式(low confinement regime,L 模)向H 模转换的阈值,进而可在L 模实现类似H 模的高比压放电,同时不会出现ELM[9,10].另一方面,TCV 实验发现,NT位型下H 模放电的台基压强水平低于PT,但其ELM 频率更高,幅值更小[11].此外,NT 也有其独特的放电优势,如: 更大的外分界面、更灵活的偏滤器配置空间、更大的刮削层空间、更低的内部极向线圈磁场需求,以及偏滤器室的更大泵送电导[12]等.相关模拟工作表明,NT 可使气球模失稳,并且导致气球模第二稳定区通道完全关闭[12,13],但已有研究并未给出NT 位型下P-B 模的非线性演化特征,而P-B 模的非线性演化直接关系到ELM 爆发产生的热流和粒子流大小,故本文对此进行了详细研究.

本文通过Corsica 的TEQ 平衡模块构建了具有不同三角形变的托卡马克平衡[14],并使用BOUT++代码[15,16]对P-B 模不稳定性进行数值模拟,模拟考虑了有限电阻效应和逆磁效应,并分别讨论了不同三角形变位型条件下P-B 模的线性和非线性特征.第2 节介绍了物理模型和托卡马克平衡;第3 节详细分析了线性和非线性模拟结果;最后在第4 节给出了结论.

2 物理模型和平衡参数

模拟使用了BOUT++三场模块,在非圆截面平衡位型下求解简化的三场双流体方程组[15,16],这些方程包含了涡度U、压强P和平行磁矢势A//的演化.

方程中变量定义为

研究首先基于BOUT++模拟常用的cbm18_dens8 平衡构造了一系列具有不同三角形变的平衡,该系列平衡基本参数与JET 装置接近,其优点是可以灵活设置托卡马克实验常见的形变参数,而不用担心数值误差问题.具体参数如下: 小半径a=1.2 m,大半径R0=3.4 m,磁轴处环向磁场B0=2 T,等离子体电流IP=2 MA,拉长比κ=1.6,该拉长比参数属于托卡马克实验常见参数范围(如ASDEX Upgrade[6]和TCV[11]).通过CORSICA代码TEQ 模块[14]构建一系列具有不同三角形变参数(- 0.3 ≤δ≤0)的托卡马克平衡,如图1 分别给出了无三角形变(δ=0)和NT 位型(δ=-0.3)的磁面形状,图中绿色区域为好曲率区域(∇B2·∇P ＞0),黄色区域为坏曲率区(∇B2·∇P ＜0)[9,18].模拟中所有平衡压强分布相同,如图2 所示,该压强分布取自BOUT++模拟中常用的双曲正切函数.平衡通过Sauter 模型考虑了自举电流的影响,自举电流份额为0.5,同时保持总等离子体电流恒定[19-21],可以看出当台基压强不变时,自举电流随三角形变的变化并不明显.平衡的芯部粒子密度取n0=3×1019m-3,密度分布由ne(ψn)=n0(P0(ψn)/P0(0))0.3给出,假设离子和电子的温度和密度相等,即Te(ψn)=Ti(ψn)=P0(ψn)/2ne(ψn),其中ψn=(ψ-ψaxis)/(ψsep-ψaxis) 是归一化磁通,ψaxis和ψsep分别是磁轴和最外闭合磁面处的磁通.

图1 不同三角形变位型的磁面 (a) δ=0;(b) δ=-0.3,蓝色实线代表 ψn=0.4 到1 的磁面,归一化磁通间隔为ψn=0.1,其中 ψn=(ψ-ψaxis)/(ψsep-ψaxis),绿色区 域为坏曲率区域(∇ B2·∇P ＞0),黄色区域为好曲率区(∇ B2·∇P ＜0)[9,18],黑色虚线为中平面位置Fig.1.Comparison of magnetic surfaces with varied δ: (a)δ=0;(b) δ=-0.3.Blue lines represent the magnetic surfaces from ψn=0.4 to 1 with an interval of 0.1,ψn=(ψ-ψaxis)/(ψsep-ψaxis) is the normalized radial coordinate.The green areas show the unfavorable curvature regions where ∇ B2·∇P ＞0 and yellow areas show the favorable curvature regions where ∇ B2·∇P ＜0.Black dashed line shows the position of the midplane.

图2 压强剖面 P0 (黑色实线)和三角形变分别为 δ=-0.3(红色实线),δ=0.0 (蓝色点线)的平行电流剖面 J‖0Fig.2.The pressure P0 (black solid line) and parallel current J‖0 profiles for cases δ=0.0 (blue dotted line) and δ=0.3 (red solid line).

3 模拟结果分析

3.1 NT 对P-B 模线性增长率的影响

对于不同的三角形变(δ=-0.3—0)位型,通过P-B 模线性不稳定性计算,图3 给出了相应的线性增长率模谱,由图可知,随着三角形变的降低,在中低n(n＜ 45)模区间,线性增长率增加;但在高n(n＞ 45)模区间,P-B 模不稳定性受到抑制.由于磁面的形状由极向电流磁线圈控制,因此不同的三角形变位型下平衡极向磁场有所不同.极向磁场的上下两端受到反向电流磁线圈的作用而降低,磁面向弱场侧移动.如图1 所示,NT 位型的坏率区域(绿色区域)随三角形变降低而增大,因为坏曲率区集中在弱场侧,具有更大的平均半径,所以沿环向积分后具有更大的坏曲率空间,从而为PB 模提供更多自由能[9,22],故中低n模区间的PB 模线性增长率增大.与此同时,P-B 模不稳定性的高n模部分还受到局域磁剪切的稳定作用[23].定义外中平面局域磁剪切[21],其中,为局域安全因子,hθ为曲率半径.图4给出了不同三角形变位型的外中平面上局域磁剪切的径向变化,由图可知,随三角形变降低,台基区局域磁剪切的绝对值不断增大,其对高n模的稳定作用逐渐增强,故高n模区间的线性增长率受到抑制.

图3 不同三角形变(δ=-0.3—0)位型的P-B 模线性增长率模谱Fig.3.Linear growth rates versus toroidal mode number for δ=-0.3 —0.

图4 不同三角形变(δ=-0.3—0)位型外中平面上的局域磁剪切 sl 在径向上的变化Fig.4.Profiles of local shear sl at the outer midplane for δ=-0.3 —0.

综上所述,NT 位型引起的磁场结构变化带来更大的坏曲率区使P-B 模失稳,同时,外中平面上台基区的局域磁剪切有助于稳定高n模.该线性结果与已有模拟结果[9,13]一致.

3.2 P-B 模非线性演化特征

不同三角形变位型的托卡马克磁场结构不同,因此,由ELM 崩塌导致的湍流输运过程特性也会有差异,所以,NT 位型下的P-B 模非线性模拟对未来的NT 位型实验和对其中的ELM 物理机制的理解具有重要意义.在非线性模拟中,考虑了离子逆磁、有限电阻率和超电阻率效应,设置的初始扰动的环向模数为线性阶段最不稳定模式的模数.ELM 能量损失通常用台基能量损失(ΔWped)与台基储能(Wped)之比表示,定义为[16]

其中ψin是模拟的内边界;ψout是压强梯度最大处.

接下来,通过δ=0 和 - 0.2 两种位型的对比来阐明NT 位型的P-B 模非线性演化特征.图5为不同三角形变位型下ELM 能量损失的对数值随时间的演化,这里取ELM 能量损失的对数主要是为了更加清晰地展示ELM 崩塌的先后顺序.由图5 可知,随三角形变降低,ELM 崩塌时间提前.图6 为t=193τA时扰动压强的环向平均在极向截面的分布,此时仍处于P-B 模的线性崩塌阶段,可以发现,随着三角形变降低,极向截面上下两端(图中黑色虚线方框区域)的扰动压强增强.由于NT 位型下坏曲率区域的扩展,P-B 模扰动在小截面上具有更大的增长区域,故其不稳定性增长得更快,崩塌也发生得更早.

图5 不同三角形变位型下ELM 能量损失的对数值随时间的演化Fig.5.Time evolution of the logarithm of ELM size for different triangularity cases.

图6 (a) δ=0 和(b δ=-0.2 位型下,t=193τA 时扰动压强的环向平均在极向截面的分布.弱场侧顶部和底部区域的黑色虚线框显示了比较区域,黑色点线表示中平面位置Fig.6.Distribution of the toroidal-averaged pressure perturbation at the poloidal cross section at t=193τA for cases (a) δ=0 and (b) δ=-0.2.Black dashed frames at the top and bottom areas in the low field side show the regions for comparison.Black dotted line shows the position of the midplane.

图7 分别给出了δ=0 和 - 0.2 两种形变位型条件下扰动压强在外中平面上的二维分布随时间的演化.由于P-B 模的环向周期性,在BOUT++中只计算了圆环的四分之一区域.对比两种位型下的扰动分布可以发现,在t=100τA和t=200τA时,初始扰动始终占据主导地位,两种位型下的扰动分布具有明显的周期性;然而,在t=300τA时,无三角形变的压强扰动仍基本保持初始扰动的周期,但NT 位型下的P-B 模扰动在环向的周期性则已被破坏,P-B 模具有更明显的湍流输运特性.

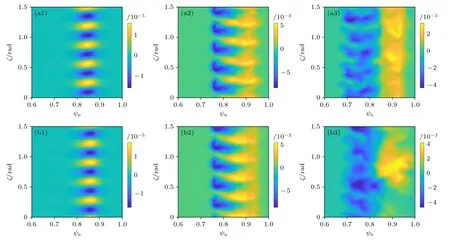
图7 (a1)—(a3) δ=0 和(b1)—(b3) δ=-0.2 在 t=100, 200, 300τA 时在外中平面上的压强扰动Fig.7.Pressure perturbation at t=100,200,300τA at the outer midplane for cases: (a1)—(a3) δ=0;(b1)-(b3) δ=-0.2.

通过对两种位型下压强梯度最大处的扰动做环向模式傅里叶分解可知,如图8 所示,在ELM崩塌阶段(t≲200τA),初始扰动模式n=20(红线)快速增长,台基压强扰动的负值部分向里移动(如图7 所示),导致压强台基崩塌.随着初始扰动模式的增长,其他环向模数的不稳定模式也被激发起来,在湍流输运阶段(t≳200τA),初始扰动模式幅值降低,n=0 模(蓝线)快速增长,能量首先转移到n=0 模,而n=0 模通常被认为是带状流,其与湍流相互作用发生能量耦合,但不会影响台基储能[24],随后,部分低n模也相继被激发.不同之处在于,无三角形变位型下被激发的不稳定模式增长并不明显,n=20 的初始扰动模式仍然在较长时间里占主导,故图7(a3)中的压强扰动仍然基本保持初始扰动的周期性;但在NT 位型下,如图8(b),n=4和n=8 的模相继增长,并依次占据主导地位,形成多种不稳定模式共存的状态.在ELM 非线性模拟中[25],通常将扰动的这种演化状态称为湍流.相比于单一模式占主导的情况,由于模式间的相互竞争,初始扰动的周期性被破坏,故在NT位型下扰动表现出更加明显的湍流输运特性.

图8 (a) δ=0 和 (b) δ=-0.2 位型下的环向模式演化Fig.8.Modes evolution for cases: (a) δ=0;(b) δ=-0.2.

4 总结与讨论

本文考虑非理想效应后,研究了NT 位型对P-B 模不稳定性的影响,得到了P-B 模在NT 位型条件下的线性和非线性演化特征,可为进一步研究NT 与等离子体约束间的作用机制提供参考.

在线性阶段,NT 位型坏曲率区域增加,导致气球模驱动源增强,同时该位型中较大的局域磁剪切有利于稳定高n模,故随着NT 的减小,P-B 模的中低n模增长率增大,这使得NT 位型下的PB 模不稳定性阈值降低,即边缘台基在较低水平时就有不稳定性增长,引发台基崩塌,从而限制了边缘台基的提升.相比之下,已有的对PT 的研究[3]发现,PT 可以增加P-B 模不稳定性阈值,进而提高等离子体约束.上述模拟结果与实验[11]中观察到的现象一致,即NT 位型下测得的边缘台基水平明显低于PT 位型.

在非线性阶段,随着三角形变降低,较大的坏曲率区导致弱场侧顶部和底部区域的压强扰动增大,扰动分布区域的扩大有利于扰动的增长,减少了ELM 崩塌所需的时间,一定程度上有利于增加ELM 频率;同时,NT 位型下多种环向不稳定模式的增长,使得ELM 具有更明显的湍流输运特性,多模共存的湍流输运状态下的扰动传播相对单一模式更弱[26],故其有利于ELM 能量损失的降低.值得一提的是,由于实验中NT 与PT 位型导致的最明显的差异之一在于边缘台基的不同,而台基高度与ELM 频率和幅值密切相关,故下一步工作将基于真实托卡马克参数(如: TCV,DⅢ-D),结合实验测量的台基剖面,分别模拟NT 和PT 位型对P-B 模的影响,以期为未来NT 位型下的高约束放电优化提供理论依据.