基于共振波导光栅结构准连续域束缚态的低阈值纳米激光器的数值研究*
2023-03-05闫梦孙珂宁廷银赵丽娜任莹莹霍燕燕
闫梦 孙珂 宁廷银 赵丽娜 任莹莹 霍燕燕
(山东师范大学物理与电子科学学院,山东省光学与光子器件技术重点实验室,山东省光场调控工程技术中心,济南 250358)
纳米激光作为一种纳米级相干光源,是光电集成芯片的关键器件.激光器进一步小型化的阻碍在于随着激光器谐振腔体积的减小,其损耗迅速增大.连续域束缚态(bound states in the continuum,BICs)能有效降低全介质结构的辐射损耗.本文提出一种基于全介质共振波导光栅(resonant waveguide grating structures,RWGs)准BIC 的纳米激光器,可有效降低纳米激光器的阈值.将传统两部分光栅转换为四部分光栅,可激发波导结构的准BIC 模式.本文数值研究了该模式的受激辐射放大特性.结果表明: TE 偏振光照射下,基于四部分光栅的RWG 结构的纳米激光阈值比基于传统RWG 结构的阈值低20.86%.TM 偏振光照射时,阈值比传统RWG结构降低了3.3 倍.而且TE 偏振光照射时纳米激光的阈值比TM 偏振光照射时阈值大约低一个数量级,这是因为TE 偏振光照射时,结构的电场局域在波导层内,增强了光与增益材料的相互作用,从而降低了纳米激光的阈值.
1 引言
半导体纳米激光器作为一种纳米级相干光源,是未来光电集成芯片的关键器件[1-3].半导体纳米激光器尺寸的进一步减小受到辐射损耗的限制[4].近年来,全介质超材料能够克服金属纳米结构的欧姆损耗而引起众多研究者的广泛关注[5-7].它们通过近场耦合产生强电磁共振而被广泛应用于纳米光子器件[8].然而,其较高辐射损耗降低了共振模式的品质因子(Q因子)和光与物质相互作用的效率[9,10].连续域束缚态(bound states in the continuum,BICs)是一种处于连续域而保持局域性的一种奇异现象,具有无限大Q值.利用BIC 能够克服高辐射损耗的问题.
BIC 现象首次在量子力学中被证明[11],1985 年第一次在实验中被发现,尽管文中并没有提到术语BIC[12].近年来,理想BIC 因其具有无限大Q因子和强局域场而受到研究者的广泛关注[13,14].BIC 存在于理想的无损结构或参数取极值时,需要打破对称保护将其转变为准BIC 才能被应用到传感器[15,16]、滤波器[17]、吸收器[18]和增强非线性效应[19]等各个领域.准BICs 由于其较小的损耗,也非常适用于实现低阈值的纳米激光器.例如,利用非对称的砖型颗粒对、圆盘以及偏心环、光子晶体等二维超表面的准BIC 模式均实现了低阈值的纳米激光[20-24].Zhang 等[25]利用上下对称分布光栅的准BIC 实现了纳米激光并将其应用于气敏传感器.
目前准BICs 大多通过二维超表面结构实现.近年来,研究人员发现一维共振波导光栅结构(resonant waveguide grating structures,RWGs)也能够激发准BICs[26-28].它们不仅具有高Q因子,而且场可以局域在波导结构中,进而增强光与物质的相互作用.共振波导光栅结构由于其高度的光学可调性以及丰富的制备工艺,被广泛应用于传感器、偏振器、波片、光电探测器、光谱仪、滤波器、激光镜等各个领域[29].本文通过数值仿真研究了一种基于四部分光栅的RWG 结构准BIC 的纳米激光,该结构相比于支持准BIC 的三维和二维的超表面更易制作.四部分光栅的RWG 结构在TE偏振光和TM 偏振光照射下均能支持高Q因子的准BIC[26,27].结合增益介质磷化铟(indium phosphide,InP),采用时域有限差分(finite-difference time domain,FDTD)数值模拟方法研究了纳米结构的激光行为.TE 偏振光照射下的纳米激光阈值与传统光栅相比下降了20.86%,TM 偏振时降低了3.3 倍.但TE 偏振光照射时纳米激光器的阈值却比TM 偏振时大约低一个数量级.
2 模型结构和方法
图1 为四部分光栅的RWG 结构单元的示意图,由四部分光栅层和波导层组成.四部分光栅的周期P=360 nm,厚度hg=40 nm.第一和第三部分为光栅的脊,宽度为da;第二和第四部分为光栅狭缝,宽度分别为db和dc.光栅的周期P=2da+db+dc.设置da=0.2P,db=d+Δd,dc=d— Δd,其中d=0.3P.本文定义了一个可调几何参数δ=Δd/d,δ∈[0,1],以便调整光栅结构.当0 <δ< 1时,光栅是周期为P的四部分光栅;δ=1时,光栅变为周期为P的两部分光栅;δ=0 时,光栅变为周期为P/2 的两部分光栅.波导层厚度hw=105 nm.由于InP 材料具有较高的折射率(n=3.3)且跃迁带隙处于近红外波段,文中选择InP 作为光栅脊的材料[30].为了简化共振波导光栅结构的制作过程,波导层材料也设置为InP.光栅的第二和第四部分为空气,波导层下面为SiO2衬底层,其折射率ns=1.45.利用时域有限差分法(FDTD)计算了全介质RWG 结构的反射光谱和激光特性.计算过程选取RWG 结构的一个周期作为仿真域,仿真域的x方向上采用周期边界条件,y方向上设为完美匹配层(perfectly matched layer,PML)边界条件.入射平面是x-o-y平面.TE 偏振(电场平行于z方向)和TM 偏振(磁场平行于z方向)光以入射角θ=5°入射到结构上.
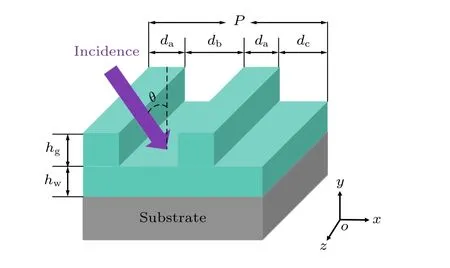
图1 硅衬底上四部分光栅的RWG 结构单元及入射光示意图Fig.1.Schematic diagram of the four part-grating RWG structure and incidence light on a silica substrate.
对无穷大平板波导结构的TE0和TM0模式的色散关系为[31]
其中,nwg,n0,ns分别为波导层、包层和衬底层的折射率,hwg为波导层的厚度.k0为空气中的波矢量,β为波导层模式的传播常数.TE0和TM0色散关系如图2 中黑实线所示,图中的ω0=2πc/hwg,c为真空中的光速,ω为入射光角频率,kx=k0x=k0sinθ为空气中波矢量的x方向分量,其色散曲线位于波导模式色散曲线之上,如图2 中彩色实线所示.此时入射光波矢量与波导模式的波矢量不匹配,波导模式不能被激发.在波导层上方引入光栅层可为入射光提供额外波矢量,使其与波导模式波矢量匹配,从而激发波导模式.0 <δ< 1 时为四部分光栅层,为入射光增加了2π/P的波矢量,与波导模式的波矢量匹配条件为
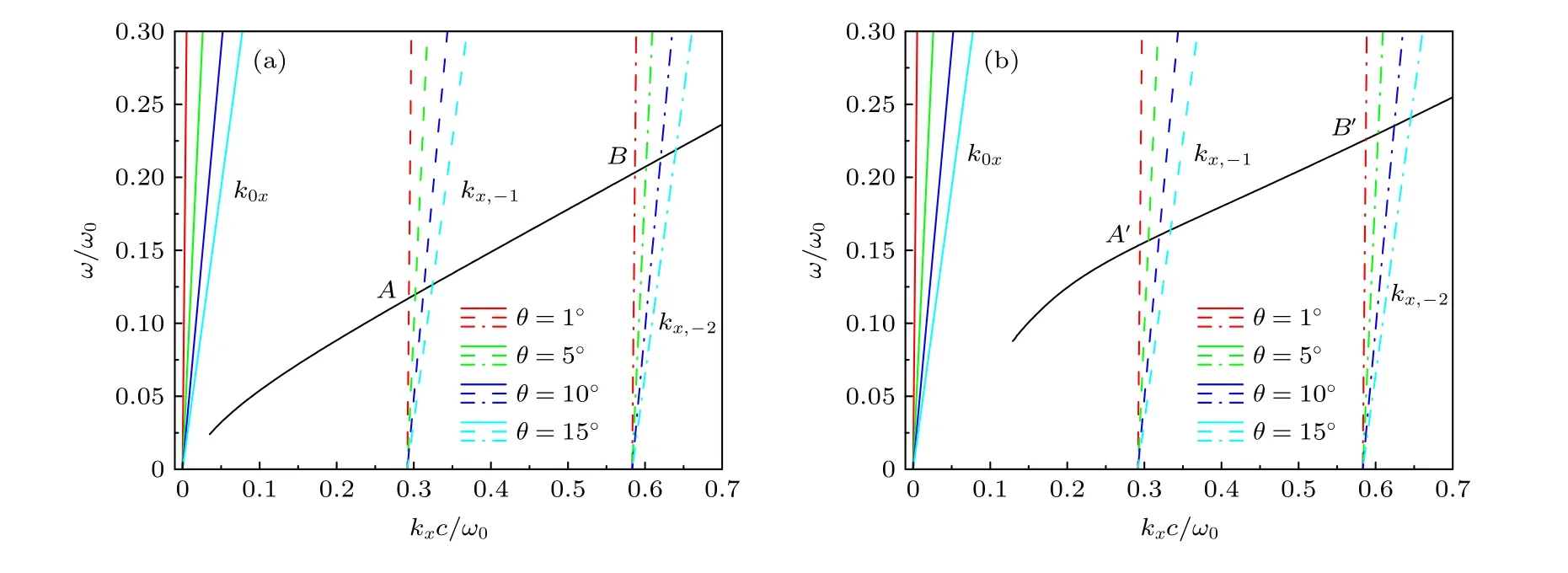
图2 波导层中TE0(a)和TM0(b)导模的色散关系曲线(黑色实线),以及在不同入射角下的kx=kx,i (i=—1,—2)色散曲线,1°(红色虚线),5° (绿色虚线),10° (蓝色虚线),15° (青色虚线).Fig.2.Dispersion relations of the TE0 guide mode (a) and TM0 guide mode (b) in the waveguide layer (black solid line),and kx=kx,i (i=—1,—2) under different angle of incidence,1° (red dashed lines),5° (green dashed lines),10° (blue dashed lines),15° (cyan dashed lines),respectively.
kx,i的色散曲线如图2 彩色虚线所示.虚线与黑色实线的交点处可满足波矢匹配条件,如图2 中点A(A')和B(B')所示,此时波导模式能被激发.图2 所示只有—1 和—2 阶波导模式可被激发.在不同的入射角θ=1°,5°,10°,15°下,TE 模式对应的角频率分别为:ωA=0.117ω0(λA=897 nm),0.119ω0(879 nm),0.123ω0(854 nm),0.126ω0(833 nm)和ωB=0.203ω0(λB=517 nm),0.208ω0(505 nm),0.213ω0(493 nm),0.219ω0(479 nm).而TM 模式对应的角频率为:ωA′=0.154ω0(λA′=682 nm),0.157ω0(670 nm),0.16ω0(656 nm),0.164ω0(640 nm)和ωB′=0.226ω0(λB′=465 nm),0.23ω0(456 nm),0.235ω0(447 nm),0.241ω0(436 nm).
当可调几何参数δ=0 时,光栅的第二和第四部分宽度相等.四部分光栅变为传统两部分光栅,周期变为P/2,此时波矢匹配条件变为
当δ≠ 0 时,传统两部分光栅的色散关系曲线与四部分光栅的偶数阶色散关系曲线重叠.即图2 中的点B(B')在两种情况下均可满足波矢匹配条件,而A(A')点只有在δ≠ 0 时才可满足.因此,当可调几何参数δ由非零变为零时,A(A')处的谐振模式变为暗模式,即BIC 模式.当δ≠ 0时,暗模泄漏,形成准BIC 模式.与对称破坏形成的准BIC 相比,四部分光栅的RWG 结构可以在不破坏面内反转对称性的情况下获得准BIC[27].
3 结果与讨论
3.1 准 BIC
当入射角为5°时,计算了不同几何参数δ的RWG结构的反射光谱,如图3(a)和(b)所示.当TE 和TM 偏振光照射时,其反射谱都呈现出Fano 线型的共振峰,且当δ=0 时,反射谱均为宽光谱.TE偏振光照射下,δ=0.1 时,在波长λ=953.07 nm处出现一尖锐的共振峰,这对应于—1 阶谐振波导模式,其共振波长比图2(a)中色散关系预测的值略大,是因为波导层上方的光栅层导致上方包层的有效折射率略有增大[27].当几何参数δ从0.1 增大到0.8 时,共振峰位置由953.07 nm 蓝移到944.39 nm,并且变得越来越宽,这是因为光栅层的折射率分布随着δ的增大而增大,也增大了衍射场与漏波导模之间的耦合作用.当δ=1 时,光栅变为传统的二部分光栅,此时的共振峰变为光栅的亮模.图3(b)所示为TM 偏振光照射下,不同δ的RWG 结构的反射光谱.可以看出,其光谱特征与TE 偏振光照射时的相似,只是当δ从0.1 增大到1 时,共振峰从695.95 nm 红移到700.94 nm.

图3 (a)(b) θ=5°时,不同几何参数δ 下的RWG 结构在TE(a)和TM(b)偏振光照射下λA 的反射谱;(c)在TE 和TM 偏振光照射下RWG 结构的Q 因子与δ 的函数关系;(d) δ=0.2 时RWG 结构分别在TE 和TM 偏振光照射下的共振波长与入射角的关系Fig.3.(a)(b) Reflection spectra near λA of the RWG structure for different geometric parameters δ at θ=5° under TE-(a) and TM-polarized (b) light irradiation;(c) Dependence of Q-factor of the RWG structure on δ under TE-and TM-polarized light irradiation;(d) δ=0.2,the relation of resonance wavelength with the angle of incidence at the RWG structure under TE-and TM-polarized light irradiation.
此外,计算了RWG 结构的Q因子(Q=λpeak/Δλ,Δλ=|λpeak-λdip|)随δ的变化情况,如图3(c)所示.TE 偏振光照射下,当 δ=1 时,Q因子约为69.8,此时的波导模式为亮模,Q值较低.当δ从1 减小到0.05 时,Q因子迅速从69.8 增大到7.72×104.当δ减小到0 时,共振峰完全消失,Q因子趋于无穷大,这与BIC 模式的特点相符.通过将BIC 转变为准BIC,可获得超高Q因子的共振模式.对于RWG 结构,可通过将δ无限接近于零来获得具有较高Q因子和较强局域场的共振模式.同样的,对于TM 偏振光照射,当δ从1.0 减小到0.05 时,Q因子也从158.1 迅速增大到2.15×104.当δ减小到0 时,谐振模式也变为了BIC 模式.图3(d)计算了δ=0.2 的RWG 结构分别在TE和TM 偏振光照射下的共振波长与入射角的关系.可以看出,TE 偏振光照射,当入射角1°增大到15°时,准BIC 共振模式的波长由941.3 nm 红移到995.9 nm;TM 偏振光照射时,入射角1°增大到15°时,准BIC 共振模式的波长由704.7 nm 蓝移到667.45 nm,这提高了该结构共振波长可调谐性.
图4 为不同几何参数下的RWG 结构的场分布情况(E/E0和H/H0).图4(a)为TE 偏振光照射下该结构的电场分布.随着几何参数δ从1.0 逐渐减小到0.1,电场从3.7 逐渐增大到76.5.随着δ的减小,衍射场与漏波波导模之间的耦合减小,电场越来越局限在波导层内.图4(b)为TM 偏振光照射下该结构的磁场分布.可以看出,随着δ的减小,磁场在波导层中的局域化程度也越来越强.当δ减小到0.1 时,磁场强度可增强到137.然而,此时结构的电场却主要分布在波导层的上下表面.尽管TM 共振模式也具有较高的Q因子,但其电场分布不利于与增益材料的相互作用,会导致纳米激光器的阈值增大.
图5 所示为δ=0.1 时RWG 结构的本征色散.图5 的两条分支分别代表波导中向两个方向传播的导模模式,其中高频的那条分支对应前面计算的波导模式.Г点处即为BIC 模式,其他点处为准BIC 模式[32].δ=0.1 时对应的准BIC 模式即为图5 中黑色圆圈处所示.插图所示为该点处的本征模式,与图4 中计算的场分布完全一致.
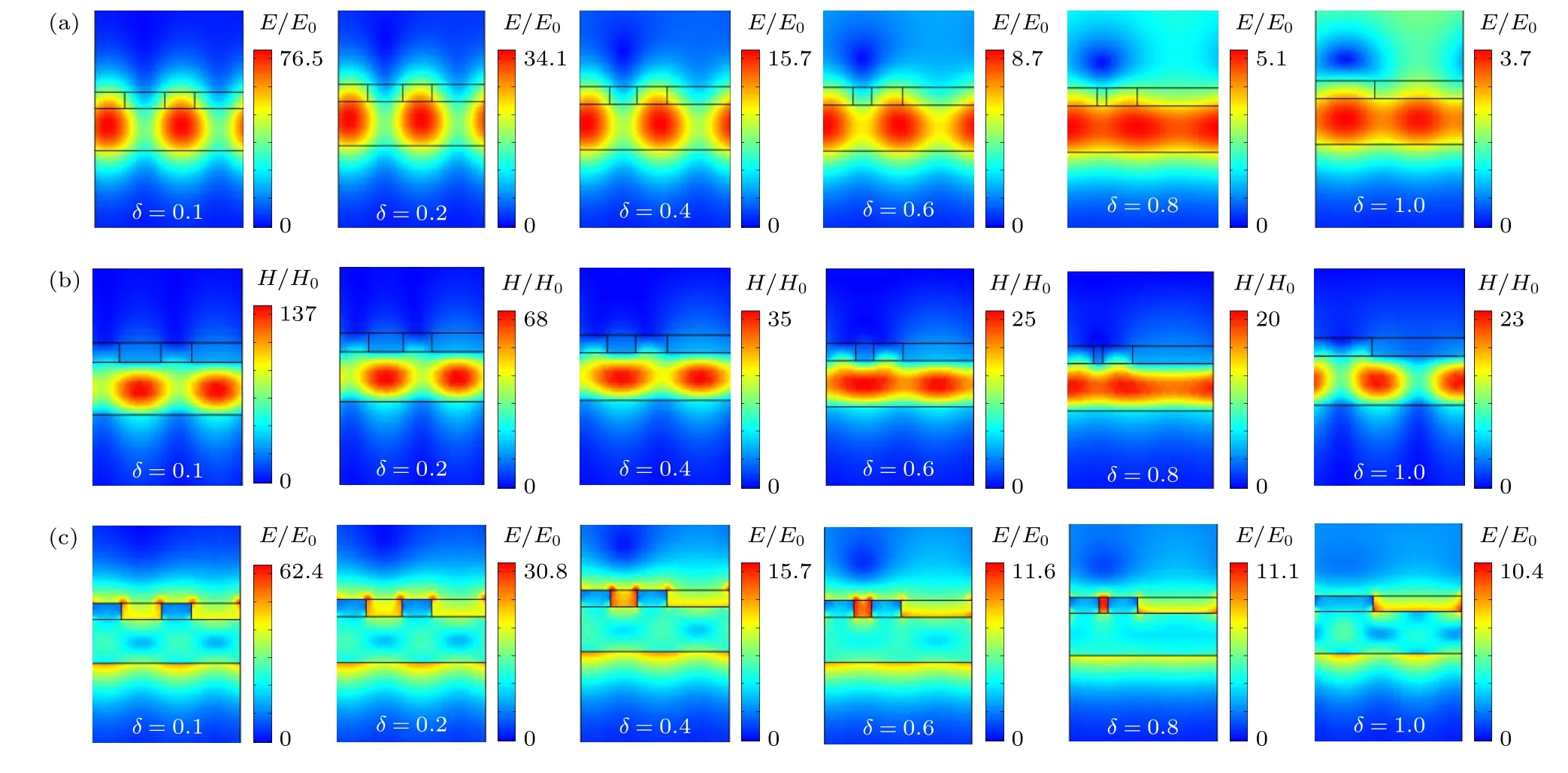
图4 (a)TE 偏振光照射时,RWG 结构在不同几何参数δ 下反射峰处对应的电场(E/E0)分布;(b)(c) TM 偏振光照射时,RWG结构在不同几何参数δ 下反射峰处对应的磁场(H/H0) (b)和电场(E/E0) (c)分布Fig.4.(a) The electric field (E/E0) distribution corresponding to the reflectance peaks of the RWG structure with different δ under TE-polarized light irradiation;(b)(c) The magnetic field (H/H0) (b) and the electric field (E/E0) (c) distributions corresponding to the reflectance peaks of the RWG structure with different δ when under TM-polarized light irradiation.
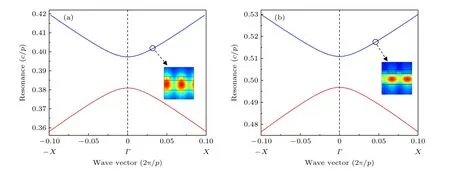
图5 δ=0.1 时RWG 结构分别在TE(a)和TM(b)偏振光照射下所支持的BIC/准BIC 模式的能带结构.黑色圆圈处为准BIC模式,插图为该处的电场(TE)和磁场(TM)分布Fig.5.δ=0.1,the band structure of the BIC/quasi-BIC mode supported by the RWG structure under TE-(a) and TM-polarized(b) light irradiation.The black circle corresponds to the quasi-BIC mode.The insets show the electric field (TE) and magnetic field(TM) distribution of the quasi-BIC modes.
3.2 激射性质
采用FDTD 方法研究了基于四部分光栅的RWG 结构的纳米激光的激射特性.将增益介质InP 描述为图6 所示的四能级系统,在能级1 和2 之间形成粒子数反转,出现激射现象.泵浦光将InP 的电子从0 能级激发到3 能级,然后无辐射跃迁到2 能级.因为粒子从能级3 到能级2 的跃迁要比从能级2 到能级1 的跃迁快得多,这将导致能级2 和能级1 之间的粒子数反转.从能级2 到能级1 的跃迁将为谐振模式的放大提供必要的能量.各能级粒子数密度随时间演化可以用以下速率方程描述[33]:

图6 半导体增益介质InP 的能级图Fig.6.The energy level diagram of the semiconductor gain medium InP.
其中,Ni是第i能级的粒子数密度,τij是能级i与能级j间的弛豫时间;Pa和Pb表示由能级2 到能级1 和能级0 到能级3 的跃迁引起的净宏观极化强度;ωa和ωb表示能级2-1 和能级0-3 之间的能量差所对应的角频率;E是总电场,它对粒子数密度的变化非常重要.泵浦光设置为连续波,入射角为5°,中心波长为838 nm,此波长对应于InP 的吸收峰[34].采用III-V 型半导体磷化铟(InP)作为增益介质,相应的参数设置为[33,34]:ωa=1.973×1015Hz,ωb=2.248×1015Hz,τ21=τ30=300 ps,τ32=τ10=100 fs,N0=5×1023m-3.
InP 的光致发光光谱谱线较宽,其中心波长与TE 偏振照射下的准BIC 共振峰重合[34],其电子向下跃迁的能量可补偿共振模式的损耗.准BIC 谐振模具有较高Q因子和较强的场局域性,能增强与增益材料的相互作用,降低激光阈值.图7 所示为基于准BIC 的RWG 结构分别在TE 和TM 偏振光照射下的纳米激光的激射行为.图7(a)为TE偏振光照射下,参数为P=360 nm,hg=40 nm,hw=105 nm,δ=0.4 的RWG 结构的归一化发射光谱随泵浦光功率密度的变化情况.当泵浦功率较低时,结构的发射光谱较宽,随着泵浦功率的增大,发射光谱逐渐变窄,当增大到9.82 kW/cm2时,发射光谱强度突然增大,此强度即为纳米激光的阈值.需要说明的是,与准BIC 共振峰相比,激射发光峰红移到958.74 nm,这是由于增益材料的加入而引起的.图7(b)所示为归一化的最大发射强度和共振峰线宽随泵浦功率密度的变化情况,并清楚地显示了纳米激光器的阈值.插图所示为泵浦功率等于9.82 kW/cm2时,RWG 结构的电场分布强度相比无增益时约增强1.2×108倍.图7(c)和(d)所示为RWG 结构在TM 偏振光照射下纳米激光的激射行为.在TM 偏振光照射下,δ=0.4 时,准BIC共振峰在697.3 nm 处,为了将结构的共振峰调至InP 的荧光峰处,将结构参数调整为:P=500 nm,hg=50 nm,hw=143 nm.可以看出,纳米激光的激射行为与TE 偏振时相似,都表现出激光系统的典型受激发射行为.但此时纳米激光的阈值约为90.95 kW/cm2,几乎比TE 偏振照射下的纳米激光阈值高一个数量级.这是因为对于TM 谐振模式,磁场主要分布在波导层中,但电场主要局域在波导层的上下表面,不利于模式与增益材料的相互作用,所以阈值增加.图7(d)中的插图显示了RWG结构在阈值90.95 kW/cm2时的磁场,与无增益相比强度增强了7.5×109倍,这意味着TM 偏振时,准BIC 模式也可以被受激辐射放大,只是需要更大的能量.
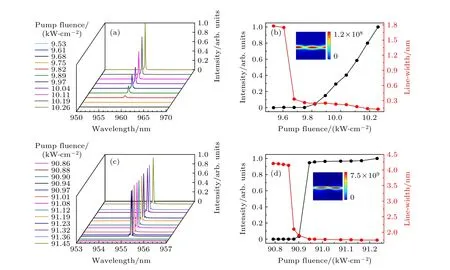
图7 TE (a)(b)和TM (c)(d)偏振光照射时,基于四部分光栅的RWG 结构的纳米激光器的激射行为;(a)和(c) 归一化发射光谱随泵浦光功率密度的变化;(b)和(d) 归一化的最大发射强度和共振峰线宽随泵浦功率密度的变化.插图为阈值处的电场和磁场分布Fig.7.Lasing actions of the four part-grating RWG structure under TE (a)(b) and TM-polarized (c)(d) light irradiation;(a)(c)Evolution of the normalized emission spectra as a function of pump optical power density;(b)(d)Evolution of the normalized maximum emission intensity and emission spectra line-width as a function of pump fluence.The insets show the electric field and magnetic field distributions at threshold.
Q因子也是降低纳米激光器阈值的一个重要参数.如图3(c)所示,通过调节几何参数δ可灵活调节四部分光栅的RWG 结构的Q因子.图8 展示了不同几何参数δ的RWG 结构的纳米激光激射行为.可以看出,每条曲线都具有相同的特征,均在泵浦光功率较小时强度没有明显的变化,当泵浦功率达到一定值时,最大强度突然增加,即为典型的激光受激发射行为.如图8(a)所示,TE 偏振光照射下,当δ=1 时,光栅变为传统的两部分光栅,此时激光器的阈值为11.01 kW/cm2,当δ从1降低到0.1 时,纳米激光阈值会降低到9.11 kW/cm2,比基于传统光栅亮态模式的纳米激光阈值降低了约20.86%.图8(b)所示为TM 偏振光照射下,不同几何参数δ对应的结构的纳米激光激射行为.随着δ值从1 减小到0.1,纳米激光的阈值从135.42 kW/cm2降低到31.55 kW/cm2,相比基于传统光栅的阈值降低了约3.3 倍.
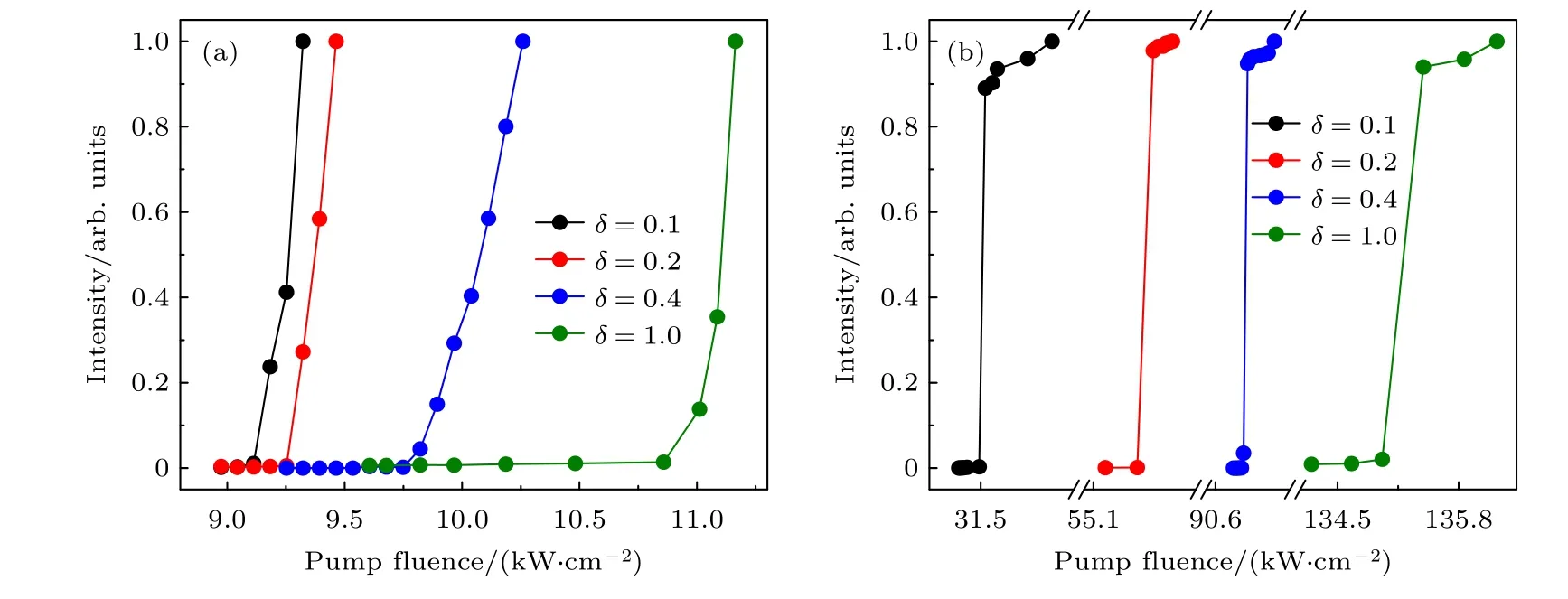
图8 TE(a)和TM(b)偏振光照射下,不同几何参数δ 的RWG 结构的归一化最大发射强度随泵浦光功率密度的变化Fig.8.The normalized maximum emission intensity of RWG structure with different geometric parameters δ under TE-(a) and TM-polarized (b) light irradiation as a function of the input pump fluence.
4 结论
本文提出了基于四部分光栅的RWG 结构准BIC 模式的纳米激光.光栅通过调节几何参数δ可由两部分光栅变为四部分光栅,此时的RWG 结构可激发波导结构的准BIC 模式.结合增益介质InP,分析了TE 和TM 偏振光照射下基于RWG 结构的纳米激光的激射行为.结果表明:TE 偏振光照射下,基于四部分光栅的RWG 结构的纳米激光的阈值比基于传统光栅的RWG 结构的阈值低20.86%,TM 偏振光照射下的阈值相比传统光栅的RWG结构的阈值降低了3.3 倍.此外,同一几何参数δ下,TE 偏振光照射时的纳米激光的阈值比TM 偏振光照射时的阈值也会低约一个数量级,这是由于TE 偏振光和TM 偏振光照射下结构的电场分布不同所致.本研究将为实现低阈值纳米激光器提供一个有效途径.
