三维深度学习网络的几何差异感知能力
2023-03-04许煜濠刘石坚康朝明吴连杰邹峥
许煜濠,刘石坚,康朝明,吴连杰,邹峥
(1. 福建省大数据挖掘与应用技术重点实验室,福建 福州 350118;2. 福建师范大学 计算机与网络空间安全学院,福建 福州 350117)
位置、朝向、尺寸是点云、三角网格等三维(three dimensional,3D)数据的基本几何属性,其差异性普遍存在。例如,图1(a)中的两个牙颌网格数据的位置和朝向即存在明显差别。使用深度学习技术处理3D数据时,如果网络模型不具备几何差异感知能力,则可能导致泛化能力不足、准确率偏低的后果。
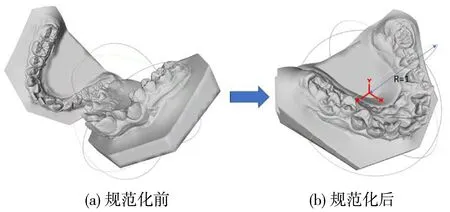
图1 牙颌网格数据规范化Fig.1 Standardization of dental meshes
通常有两种策略解决上述问题:修正数据或者修正模型。修正数据是通过人为干预,消除几何差异,避免网络模型面临该挑战。具体方法是:将数据规范化至统一的位置、朝向、尺寸,再进行训练或预测。例如,图1(b)即为对图1(a)中数据进行规范化处理后的效果。修正数据方法的局限性在于:(1)手工交互难以避免,耗时费力;(2)并非从源头解决模型的几何感知问题。修正模型的思想则是着眼于模型网络结构优化,使其从多样化的数据中学习到感知几何差异的能力。
本课题采取修正模型的策略,在分析已有相关研究的基础上,提出名为“几何差异感知(geometric difference perception,GDP)”的模块,以提升模型的几何差异感知能力;以牙齿分割为应用背景,通过主流模型进行对比实验,验证GDP的可行性和有效性。
1 相关工作
1.1 点云数据
由于点云的复杂性比三角网格要低,当深度学习方法从二维应用场景(例如处理图像数据)扩展到三维时,前期研究多关注其在点云数据上的应用。例如,Qi等人[1]所提出的PointNet即为其中的典型代表,用于实现点云分类和分割。
在PointNet中,作者提出名为变换网络(transform net,T-Net)的局部结构来解决输入模型的点云特征以及高维特征的对齐问题。如图2所示,当通道数为3(即三维坐标)的点云数据输入网络之后,将首先进行一个输入变换。该变换中的T-Net网络会输出一个3×3的变换矩阵,与原始数据进行矩阵相乘。其本质即使用上述几何变换,对输入点云进行规范化。

图2 PointNet中的T-Net迷你网络Fig.2 T-Net mini networks in PointNet
此外,网络中还有另一个包含T-Net结构的特征变换,第二个T-Net与第一个的区别在于:其输入为通道数等于64的高维特征,输出为64×64的变换矩阵,即实现高维特征空间中的规范化。
文献[2]所提出的DGCNN模型同样采用点云变换模块来估计仿射变换矩阵,将输入点集对齐到一个规范空间。与PointNet不同的是,DGCNN弃用了高维特征变换模块。
为便于区分,本研究将作用于低纬特征的T-Net记为T-Net-Ⅰ,作用于高维特征的T-Net记为T-Net-Ⅱ。
1.2 网格数据
在对三角网格进行深度学习时,目前主流的方法是以面片为样本基本单元进行处理。由于一个面片可以通过3个顶点和1个中心点共4组特征予以表征,在使用三维坐标作为原始特征的情况下,一个样本的特征尺度则为N×12(N为网格数据的面片数)。如果再加上法向量特征,则特征尺度将变为N×24。TSGCN[3]、MGFL[4]是这类方法的代表。由于使用比点云方法更多的特征数据,基于面片的方法通常性能更优,但计算资源需求更大。为此,它们仅使用T-Net-Ⅰ来应对输入数据的几何差异问题,从而降低计算量。
1.3 T-Net模块
综上可知,在应对数据几何差异挑战时,已有方法的核心思想主要是通过监督学习得到一个变换矩阵,将特征数据对齐到一个规范空间。具体是采用T-Net迷你网络实现,区别在于T-Net的数量和位置,详见表1。表1中PointNet++[5]是PointNet的升级版本,它与基于面片的网格方法GACNet[6]一样,都没有采用相关措施。若输入数据存在几何差异,则PointNet++和GACNet均无法达到理想的预测效果。
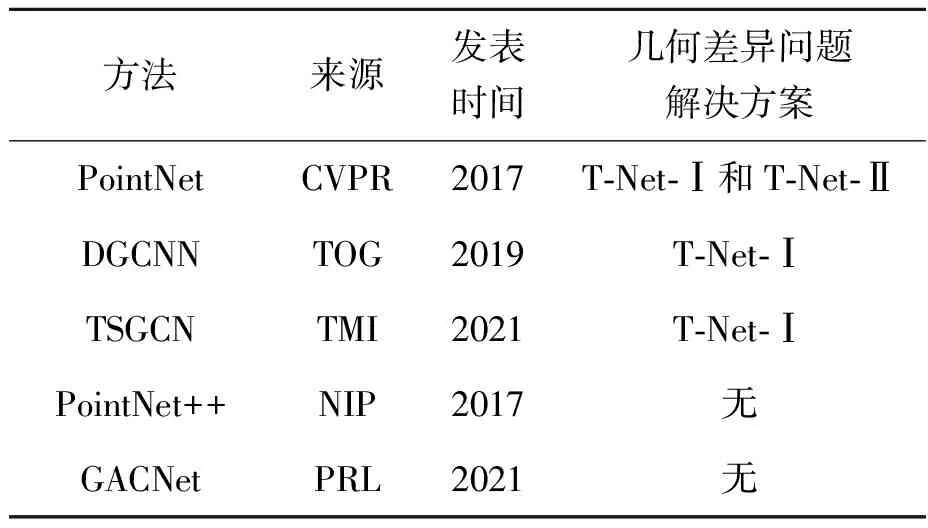
表1 相关方法信息表Tab.1 Information of related methods
图3展示了T-Net-Ⅰ在TSGCN中的网络细节。图中虚线框内的结构即为T-Net网络,它由3个卷积层、1个最大池化层和3个全连接层依次拼接而成。就特征数据而言,其输入为N×12(4组×3通道/组=12通道)的原始特征。输入数据首先通过3个卷积层,通道数逐步提升至64、128和512;然后通过最大池化操作,特征尺寸变为1×512;最后,通过3个全连接层的作用,输出为一个12×12的仿射变换矩阵。将该矩阵与输入特征相乘,即可实现特征的规范化。
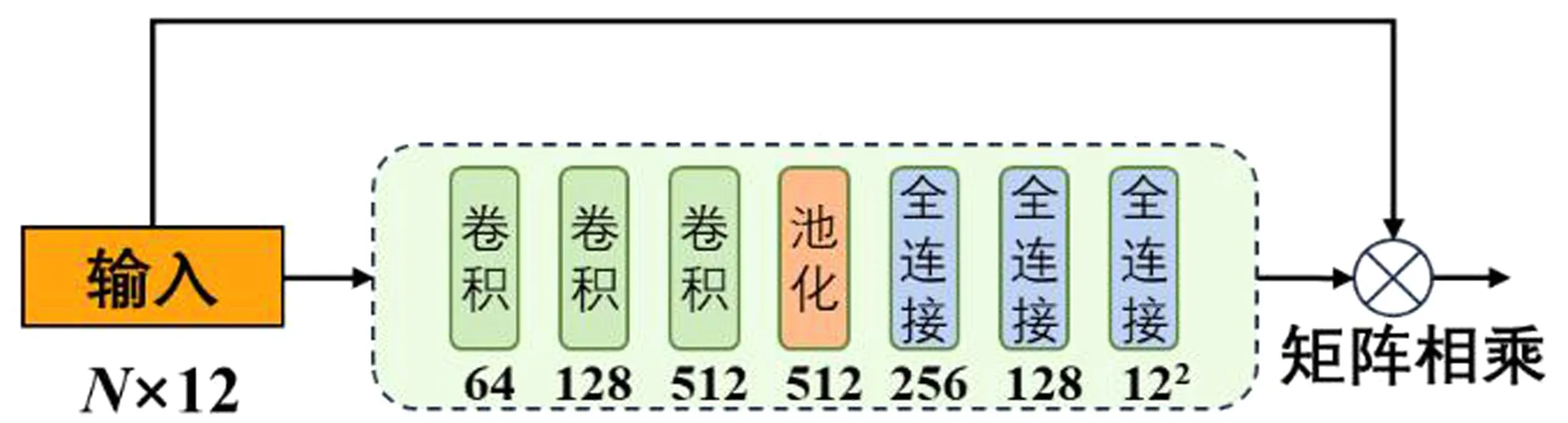
图3 TSGCN中的T-Net模块细节Fig.3 Details of T-Net adopted in TSGCN
2 几何差异感知模块及应用范例
本研究的动机是基于以下两个问题:(1)是否有必要使用多个T-Net结构;(2)如果出于计算成本考虑只选用一个T-Net,要如何进行配置。
2.1 GDP模块
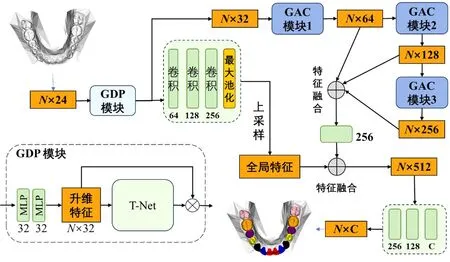
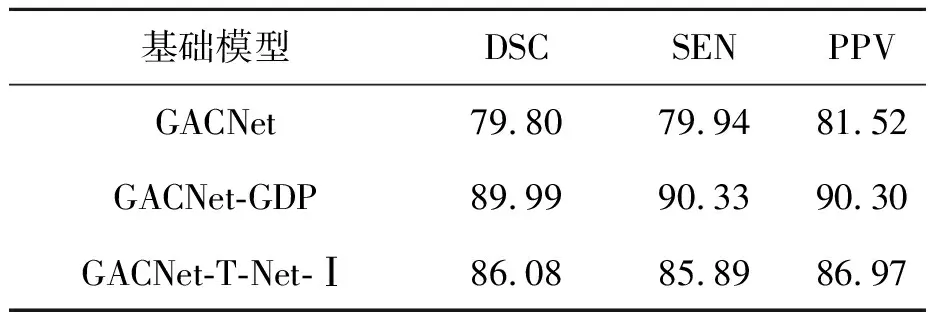
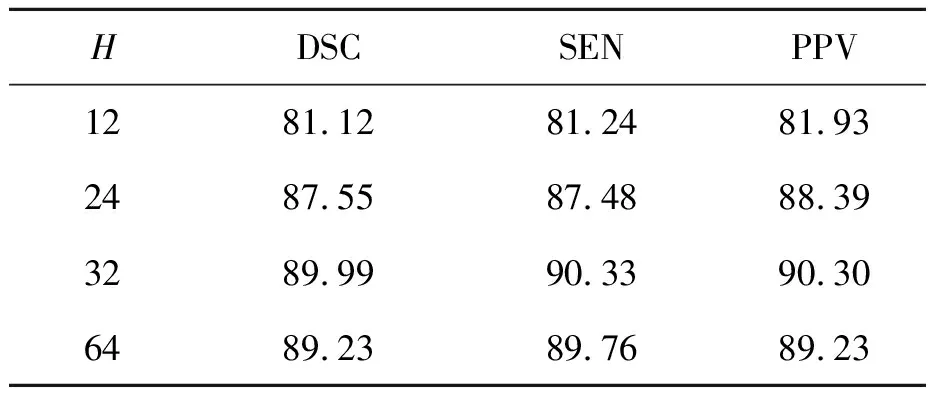
GDP模块的结构细节如图4所示,其核心思想是:使用K个维度为L的多层感知机(multilayer perceptron,MLP,如图中虚线框所示)将N×L的低维特征转化为N×H的高维特征之后,再输送给后续的T-Net网络,其中N为样本基本单元的个数,L 图4 GDP模块Fig.4 GDP module structure GDP本质上是一个作用于高维特征的T-Net。相较图3中的T-Net结构,GDP中的T-Net同样由三层卷积、一层池化、三层全连接层组成,区别在于:最后一层的维度为H2,即确保输出为H×H的变换矩阵,从而实现N×H尺寸高维输入特征的规范化。 3D牙颌网格数据记录了患者口腔中牙齿的形态信息,通过深度学习技术将单颗牙齿从牙颌网格数据中准确分割出来,对于牙齿疾病诊断、手术规划等具有重要意义[7]。 由于从不同渠道采集获取的牙颌网格数据,其尺寸、朝向、位置存在一定差异,为了验证GDP的有效性,选择未考虑几何差异问题的牙齿分割模型GACNet[6]作为改进范例。 GACNet是一种基于面片策略处理网格数据的深度学习方法。如图5所示,该网络整体上是一个双分支结构,其中包含3个图注意力卷积(graph attentional convolution,GAC)的分支用于局部特征提取,另一分支则用于全局特征提取。以牙颌网格数据上提取到的N×24的原始特征作为输入,GACNet最终将给出N×C的预测结果,其中N为面片数,C表示预设的类别数。 图5 具有GDP的GACNet改进网络结构展示Fig.5 Demonstration of improved GACNet with GDP 按照2.1节的思路,将GDP模块(细节见图中虚线框)放置于N×24的输入特征之后,分支结构之前。经实验表明,当K取2、H取值32时,性能提升效果最佳。 实验所用的数据来自MICCAI挑战赛的公共数据集3DTeethSeg[8],每个原始牙颌网格数据由100 000~300 000个数量不等的面片组成。为了便于训练,将数据统一为17 000个面片数的规模。 由于训练样本的几何差异性越丰富,模型的泛化能力越高,因此对网格数据进行包含随机角度旋转和随机坐标位移的数据扩充操作。扩充后的训练集规模为2 058,验证集和测试集分别为588和294。 所有实验均运行于一台显卡为NVIDIA Ge-Force RTX 3090(24 GB),CPU为Intel Core i9-10920X(3.50 GHz)的台式计算机上。共训练120个epoch,训练时采用Adam优化器,batch_size设为2,学习率初始为1×10-3,每20个epoch进行0.5倍衰减。 分割性能通过3个指标进行定量评估,分别为:Dice相似系数(DSC)、灵敏度(SEN)和正预测值(PPV)。令TP、TN、FP、FN分别表示真阳性、真阴性、假阳性和假阴性,DSC、SEN和PPV的计算方法分别如公式(1)(2)和(3)所示。 (1) (2) (3) 上述3个指标值与分割性能成正比,即数值越高代表性能越好,区别在于侧重点存在差异。通过对这些差异性进行评估,可以确保模型在不同数据集划分和数据增强条件下都能够稳健地完成任务目标。 为了验证GDP的效果,使用原始GACNet模型、加入GDP模块后的GACNet改进模型(记作GACNet-GDP)、以及加入T-Net-Ⅰ模块后的GACNet改进模型(记作GACNet-T-Net-Ⅰ)进行对比实验,结果如表2所示。 表2 分割准确性对比Tab.2 Segmentation accuracy comparison 得益于模型几何感知能力的提升,加入T-Net之后的分割准确率相较加入之前大幅提升。另外,相较GACNet-T-Net-Ⅰ,包含T-Net-Ⅱ的GACNet-GDP的准确率更高。该实验结果说明如果只选用一个T-Net,T-Net-Ⅱ比T-Net-Ⅰ的性能更好。 对应的可视化结果如图6所示,其中每行对应着一个典型样本,第1列是原始输入网格,第2列至4列分别为真实值、GACNet-GDP以及GACNet-T-Net-Ⅰ和GACNet的结果。从中不难发现,加入GDP之后的效果相较于其他方法更为准确,而GACNet没有针对数据的几何差异进行处理,因此存在明显差错,该结论与表2相符。 图6 对比结果的可视化Fig.6 Visualization of comparison results 由于在面片方法上测试多个T-Net的计算资源要求过高,故改用点云方法PointNet++作为基础模型进行对比实验。实验对象分别为加入GDP模块的PointNet++(记作PN++-GDP)和加入2个T-Net模块的PointNet++(记作PN++-T-Net-Ⅰ&II),实验结果如表3所示。从表3可见,使用1个包含于GDP内部的T-Net与使用2个T-Net的效果差别不大,且单个GDP计算资源要求更少,因此更适合处理网格数据。 表3 不同数量T-Net模块下的准确率对比Tab.3 Accuracy comparison with different numbers of T-Net modules GDP具有超参数K和H,其中K表示MLP的个数,H表示MLP的维度。在对GACNet的改进中两者取值分别为2和32。为验证该超参数的选择,本研究对不同取值下的结果进行对比。 3.4.1 MLP的个数选择 在H取值32的情况下,将K分别以0、1、2、3赋值,并进行分割性能对比。当K=0时,GDP退化为T-Net-Ⅰ,其余情况本质上是T-Net-Ⅱ。如表4所示的实验结果表明:(1)在T-Net前加入MLP确实能够提升性能;(2)使用2层MLP的效果较其他方案效果更优。 表4 不同MLP个数下的准确率对比Tab.4 Accuracy comparison with different numbers of MLPs 3.4.2 MLP的维度选择 在K取值2的情况下,测试不同维度MLP对性能的影响。由于输入数据的通道数是24,分别以12(降维)、24(不变)、32(升维)、64(升维)对H进行赋值,并将分割准确率记录如表5所示。 表5 不同MLP维度下的准确率对比Tab.5 Accuracy comparison with different dimensions of MLPs 实验结果表明,通过MLP对输入特征维度降低会影响模型的分割性能,导致准确率下降。保持特征维度不变或升高维度对模型则有提升作用,且当MLP的维度取32时模型精度最优。 本研究针对三维深度学习模型的几何差异感知能力进行研究,提出名为GDP的网络模块。其核心思想是通过作用于高维特征的T-Net来对特征进行规范化。将GDP应用于3D牙齿分割,实验结果表明:GDP模块能够有效应对3D数据的几何差异问题,确保模型的泛化能力。 未来将针对牙齿分割准确率提升方法进行研究,并在新方法中进一步验证GDP模块的效果。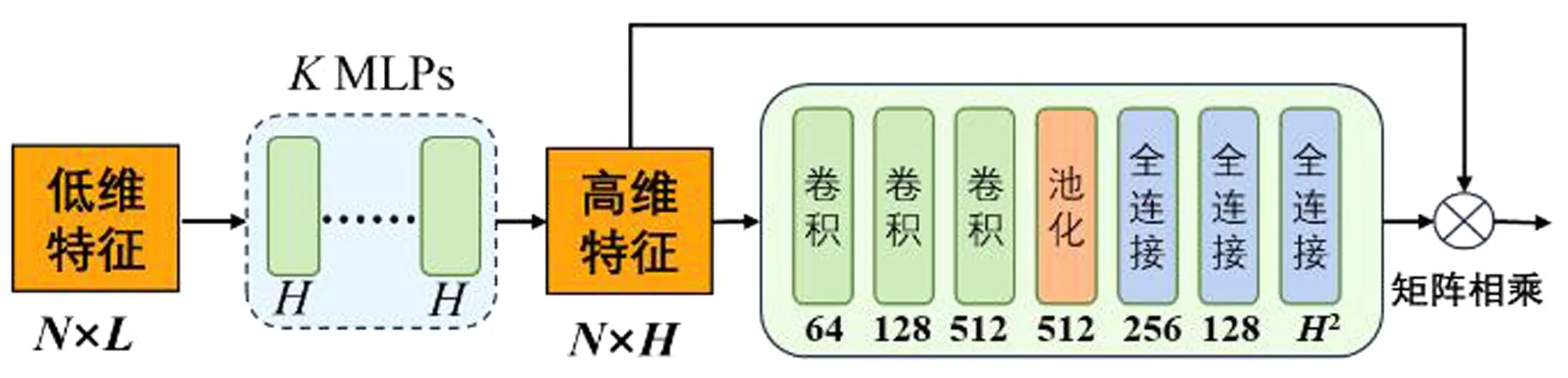
2.2 牙齿分割应用
3 实验与讨论
3.1 数据集及实验环境
3.2 评价指标
3.3 对比实验


3.4 消融实验

4 结束语
