基于HHT的复合扰动环境中结构基本自振周期优化识别
2023-03-04许言李永强周仰新刘旭锋彭聪姬雪明
许言,李永强,2,周仰新,刘旭锋,彭聪,姬雪明
(1. 东华理工大学 土木与建筑工程学院,江西 南昌 330013;2. 南昌市应急管理局,江西 南昌 330038)
我国城镇建设中积累了大量旧建筑,潜在的安全风险日益严峻且多样化。面大量广的工程设施亟需进行高效、可靠的健康监测,结构的基本自振周期是实用可靠的选择之一。工程结构振动(地震、风振等)破坏控制及优化与加固设计中,基本自振周期的准确、快速及自动识别是分析的关键和难点之一,该研究也可为结构健康状态的判别提供依据。
由于测试环境不可控,测试过程中很难避免强迫激励或人为振动,甚至测试系统本身零漂或震荡等对结构自振特性测试信号的干扰,导致脉动法采集到的脉动信号信噪比低,从而影响后续数据分析的准确性。为了获得更准确的测试结果,提升分析效率,诸多学者一直在探索高效可靠的数据处理方法。相关分析方法主要有工程振动领域常用的快速傅里叶变换(FFT)法、用于场地卓越频率研究的单点H/V谱比法、用于分析结构固有频率的顶层/首层傅里叶频谱比[1](R/F谱比法)等,以及对信号进行经验模态分解后再分析的希尔伯特-黄变换(HHT)[2]。在实际工作中,赵岩等[3]针对移动随机载荷作用下桥梁结构非平稳随机振动问题,建立了一种基于频域分析的虚拟激励-傅里叶变换方法(PEM-FFT)。吴琛等[4]从数字方法的角度论述了HHT的理论进展与工程应用。杨佑发等[5]基于HHT方法实现了对两类长周期地震动的特殊长周期成分的提取。何定桥等[6]提出了一种基于HHT的结构模态自动识别方法。丁新余等[7]利用HHT方法研究了隧道爆破作用下建筑物的振动响应规律。李传金等[8]对存在人为振动干扰的场地脉动信号,应用HHT方法进行经验模态分解,由原始数据减去IMF分量后差值的频谱峰值判别卓越周期。
综上,结合建筑结构形态特征,本文选取FFT、R/F谱比及HHT方法对建筑结构脉动信号快速处理与分析,并将分析结果进行对比,以探讨各方法的优势与局限性,为结构抗震设防及防灾减灾自动化、智能化提供参考。
1 HHT基本原理
HHT方法是由Norden E. Huang等[9]于1998 年提出的,后来又对其进行了改进[2]。这种方法核心思想是将时间序列资料通过经验模态分解(empirical mode decomposition,简称 EMD) 成数个本征模态函数(intrinsic mode function,简称 IMF),然后利用Hilbert变换构造解析信号,得出资料的瞬时频率和振幅,进而得到Hilbert谱。
1.1 经验模态分解(EMD)
设x(t)代表需要分解的信号,找出x(t)上所有极值点,用3次样条曲线连接各极大值点形成x(t)的上包络线xmax(t),同理得到由各极小值点形成的x(t)下包络线xmin(t)。
从而得到首个瞬时平均值m1(t):
(1)
用待分解的信号x(t)减去首个瞬时平均值m1(t),得到第一个去掉低频的新数列h1(t)[2]:
h1(t)=x(t)-m1(t)
(2)
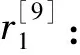
x(t)-C1=r1
(3)
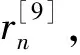
(4)
1.2 Hilbert变换
对任意一个时间函数x(t),其Hilbert变换y(t)[2]定义为:
(5)
其中,PV为柯西主值。则对应于x(t)的解析信号z(t)为:
z(t)=x(t)+y(t)=a(t)eiθ(t)
(6)
其中,a(t)称为信号x(t)的瞬时振幅;θ(t)称为信号的瞬时相位[9]:
(7)
(8)
由瞬时相位可以得到信号的瞬时频率ω(t)[9]:
(9)
对原始信号的每一阶IMF进行Hilbert变换后,原始信号可以表达成[2]:
(10)
其中,R为函数实部。此外,原始信号x(t)的表达式中,已经去除了rn,因为rn是一个单调函数或常数。
根据式(10),将信号x(t)表示在一个三维图中,在联合的时间-频率平面上,将瞬时振幅aj(t)的轮廓画出来。信号x(t)的这种时频表示即为其Hilbert谱,H(t,ω)定义为:
(11)
如果将H(t,ω)对时间积分,就可以得到Hilbert边际谱h(ω)[9]。边际谱提供了对于每个频率总振幅的量测,表达了在整个时间长度内累积的振幅。
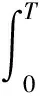
(12)
2 结构脉动测试与分析方法
2.1 结构脉动测试
选取南昌市某临街小区结构类型简单的12层住宅楼观测脉动信号。测试中检波器采用891-II型拾震器,信号采集使用DH5922N动态信号测试分析系统。
测试时间特定选择为干扰显著的白天,在建筑内设置2个测点,分别在建筑首层(F)、顶层(R)。每个测点3个正交方向均布设拾振器,分别观测建筑结构水平纵向(X)、水平横向(Y)及竖直方向(Z)的加速度成分。信号采集仪放置于建筑首层,与拾振器通过缆线连接,采样频率为200 Hz,单次测试时间保证10 min以上,仪器的布置如图1所示。

图1 仪器布设位置和方式Fig.1 Position and mode of instrument layout
拾振器布置在结构平面刚度中心处的主要承重构件附近,用于保证接收到的信号以平移振动信号为主,尽量减少扭转振动信号。F与R监测点保持在一条铅垂线上,F、R监测点的水平纵横向与建筑结构水平纵横向一致。
2.2 结构脉动数据分析方法
2.2.1 FFT功率谱计算
对测量得到的时域数据截取相同的时间长度,加矩形窗,应用FFT分别求出顶层(R)结构水平纵向(X)、水平横向(Y)的傅里叶变换功率谱PRX(ω)、PRY(ω)。
2.2.2 基于FFT的R/F谱比
对测量得到的时域数据截取相同的时间长度,加矩形窗,应用FFT分别求出首层(F)和顶层(R)结构水平纵向(X)、水平横向(Y)的傅里叶变换功率谱PFX(ω)、PFY(ω)、PRX(ω)、PRY(ω)。分别计算X和Y方向的结构顶层和首层的傅里叶频谱比,即:
(13)
(14)
FFT和基于FFT的R/F谱比都是从图中读取第一个峰值对应的频率f,其倒数为结构基本自振周期T。
2.2.3 HHT数据处理
HHT包括EMD分解和Hilbert变换。使用EMD将顶层(R)实测数据分解为IMF分量,IMF分量由结构自振响应及外荷载引起的强迫振动响应两部分构成。对IMF分量进行Hilbert变换,进而对其积分求得边际谱。
3 实测数据处理与分析
以12层住宅楼的顶层(R)水平横向(Y)数据分析为例,其加速度响应时程如图2所示。受初始分析认为无效的低频波形的影响,信号有向上浮动的趋势,产生了基线漂移。若不消除基线漂移,进行FFT分析时,会误把趋势项当作采集的原始信号,造成畸变,导致低频部分出现尖峰,甚至淹没主频成分,从而严重影响数据分析的准确性,图3为对顶层(R)实测数据未消除基线漂移直接进行FFT后的图像,由图3(a) 0~100 Hz的频率分布可看出,频谱图中有多个主峰,且能量分布较分散。图3(b)为0~10 Hz的频率分布,0 Hz 附近出现尖峰,为结构基本自振周期自动分析及后续使用带来了不确定性。
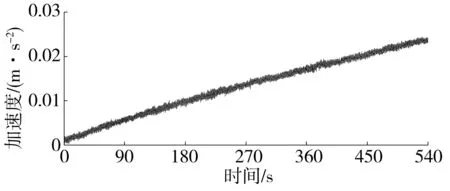
图2 顶层(R)水平横向(Y)的加速度响应时程Fig.2 Acceleration response time history of the top layer (R) horizontally (Y)
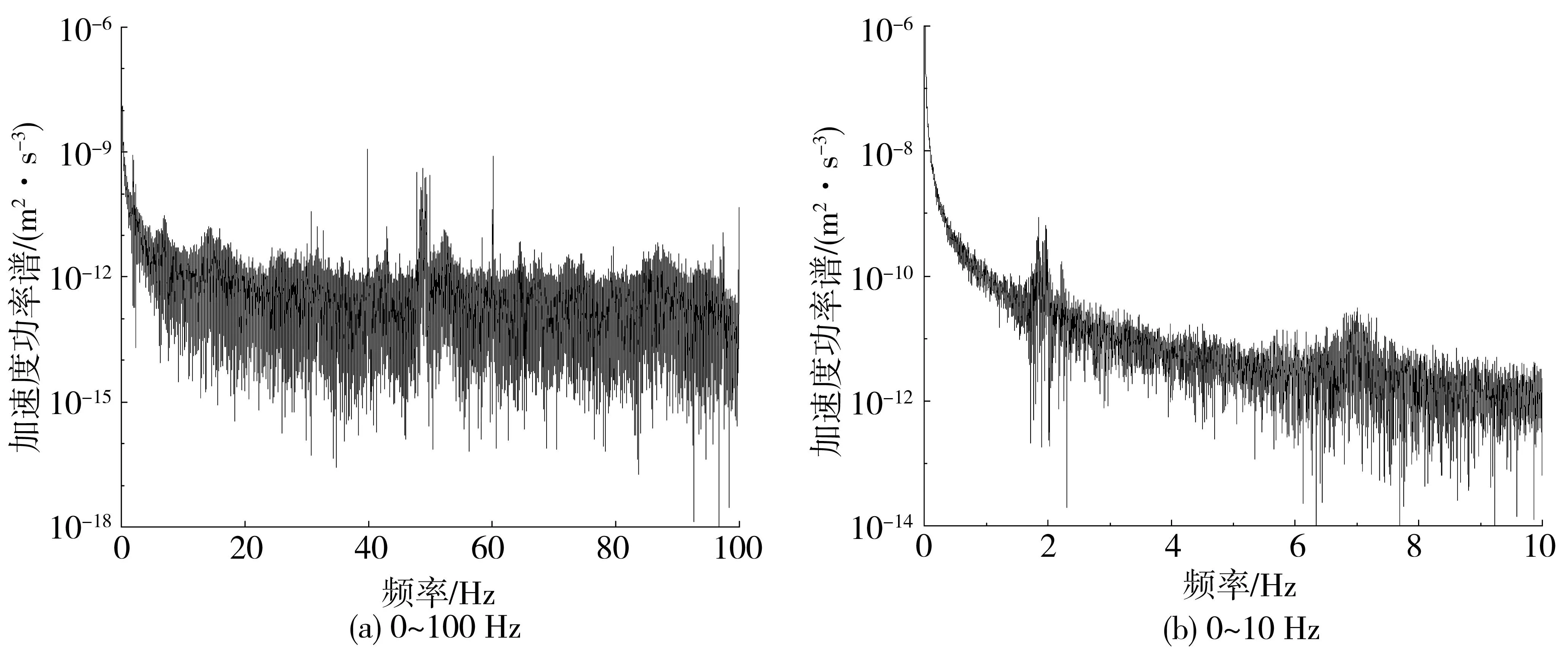
图3 顶层(R)水平横向(Y)的FFT功率谱Fig.3 FFT power spectrum of the top layer (R) horizontally (Y)
通过上述方法可得到首层(F)水平横向(Y)实测结构脉动数据的FFT后的功率谱,再按照式(14)得到该结构Y方向的R/F谱比。图4为首层(F)水平横向(Y)的FFT功率谱,图5为顶层(R)与首层(F)水平横向(Y)的功率谱比。

图4 首层(F)水平横向(Y)的FFT功率谱Fig.4 FFT power spectrum of the first layer (F)horizontally (Y)
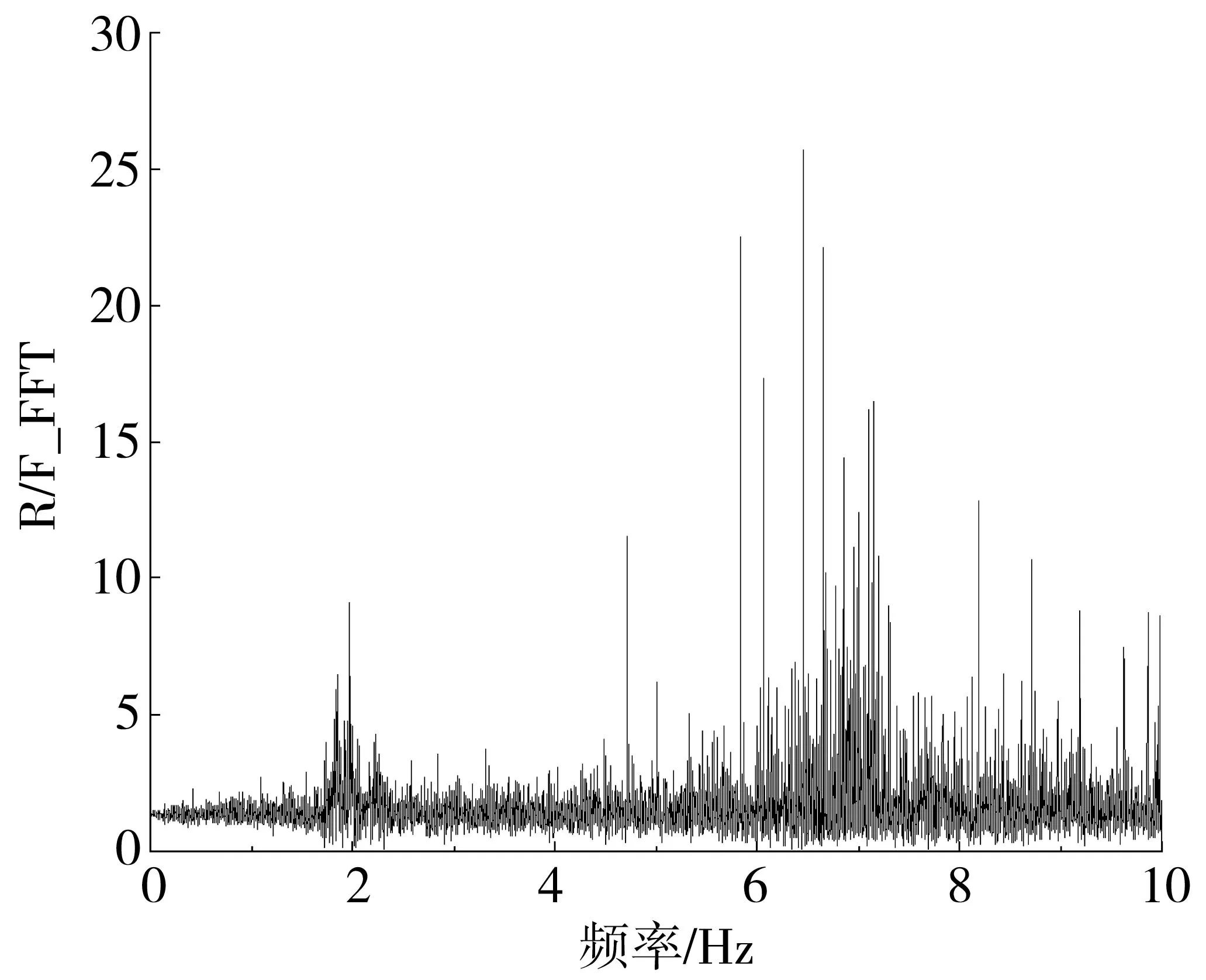
图5 顶层(R)与首层(F)水平横向(Y)的功率谱比Fig.5 Power spectrum ratio of the top layer (R) and the first layer (F) horizontally (Y)
由图5可见,基线漂移有较好改善,主峰相较于图3(b)更加凸显,显示结构的第1阶频率在1.5~2.5 Hz之间。由于谱比的原因,图5中在6.5 Hz处有一个明显的谱比增强带,而实际上由图3(b)可知其反应要显著低于“第一个峰值”处的功率谱值,因而,谱比法为自动识别和后处理带来了新的干扰。
对原数据进行EMD分解,得到10个IMF分量及余项,图6展示了顶层(R)水平横向(Y)测试数据的前5个IMF分量及一个余项。所有分量的Hilbert谱如图7所示,Hilbert变换后得到的幅值-频率-时间三维分布如图8所示,能量越高颜色越亮,实测信号中,非结构固有的高频信号能量显著,值得注意的是,在图7中2 Hz附近依然存在较为明显的频率条带,为结构固有的低频率成分。
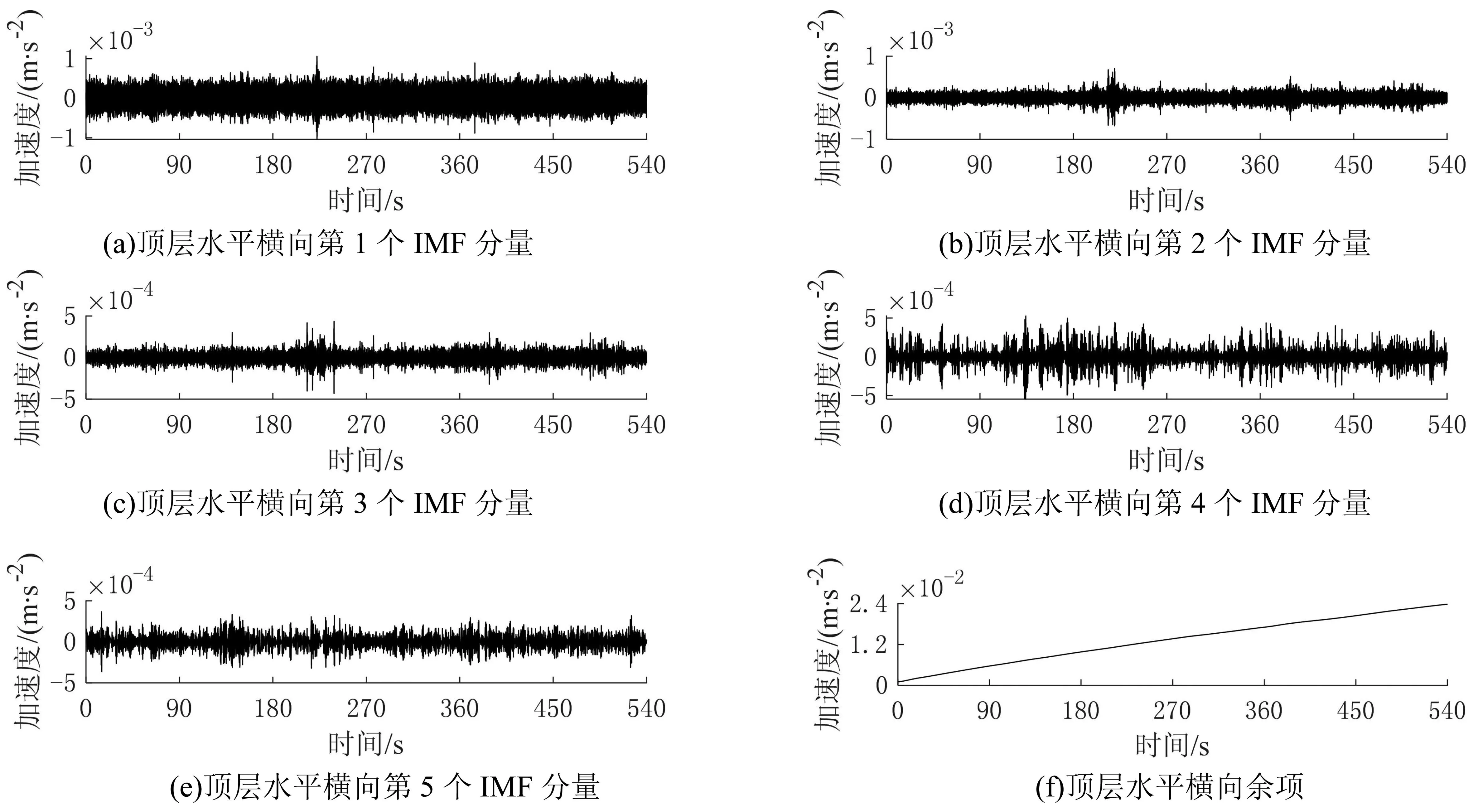
图6 EMD后的前5个IMF分量和余项Fig.6 The first 5 IMF components and remaining items after EMD
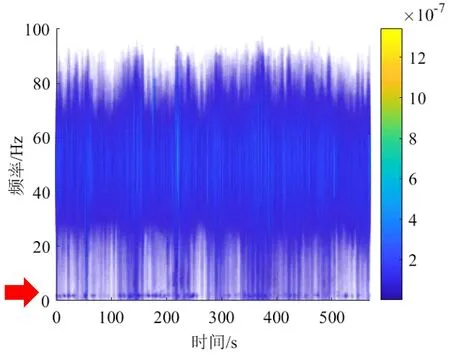
图7 所有分量的Hilbert谱Fig.7 Hilbert spectra of all components
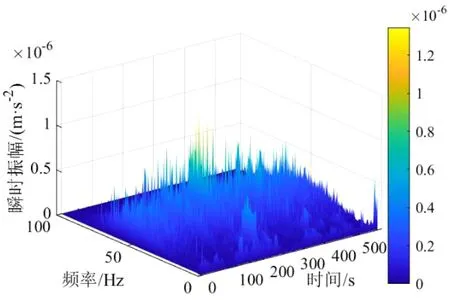
图8 Hilbert变换后得到的幅值-频率-时间三维分布Fig.8 Three-dimensional distribution of amplitude-frequency-time obtained after Hilbert transformation
对各IMF分量FFT分析后,得到各分量频谱图,图9展示了前5个IMF分量经FFT后的频谱图。可以看出,各图像中主峰突出,且能量较为集中,先分解出高频部分,然后频率依次降低。排除IMF各分量中非结构固有的高频部分,结合结构第1阶固有频率相对范围,IMF4所对应的FFT图像更加清晰地展示了该结构水平横向频谱图中第一个峰值为1.85 Hz。EMD分解出分量后,进行识别和选取,从建筑结构基本自振周期范围,选择出更精确的结果。

图9 前5个IMF分量FFT后的频谱图Fig.9 Spectrum diagram after FFT of the first 5 IMF components
对分解出来的IMF4信号经Hilbert变换后得到了幅值-频率-时间的函数关系,由式(12)得到了IMF4的边际谱如图10黑线所示。同时,图10中给出了基于FFT的R/F谱比结果,为方便对比,已将两者进行归一化处理。在未处理噪声的前提下,两种方法都表现处了良好的波峰形态,且两者的第一个主峰对应的频率基本一致。由于IMF4是经过EMD分解得到的信号分量,故其峰值单一清晰更易判别,而基于FFT的R/F谱比的频率分布中,4~10 Hz部分仍有比较显著的多个信号频率,若为固有频率较高的低层建筑,可能会出现频率混淆的情况,造成不易识别的困扰。此外,HHT方法仅需建筑结构顶层的脉动信号即可进行分析,相较于需要同时实测两个测点的R/F谱比方法,其不需要用更长的缆线连接设备并部署更多的拾振器,更加省时省力,对重要结构持续观测具备良好的经济性。
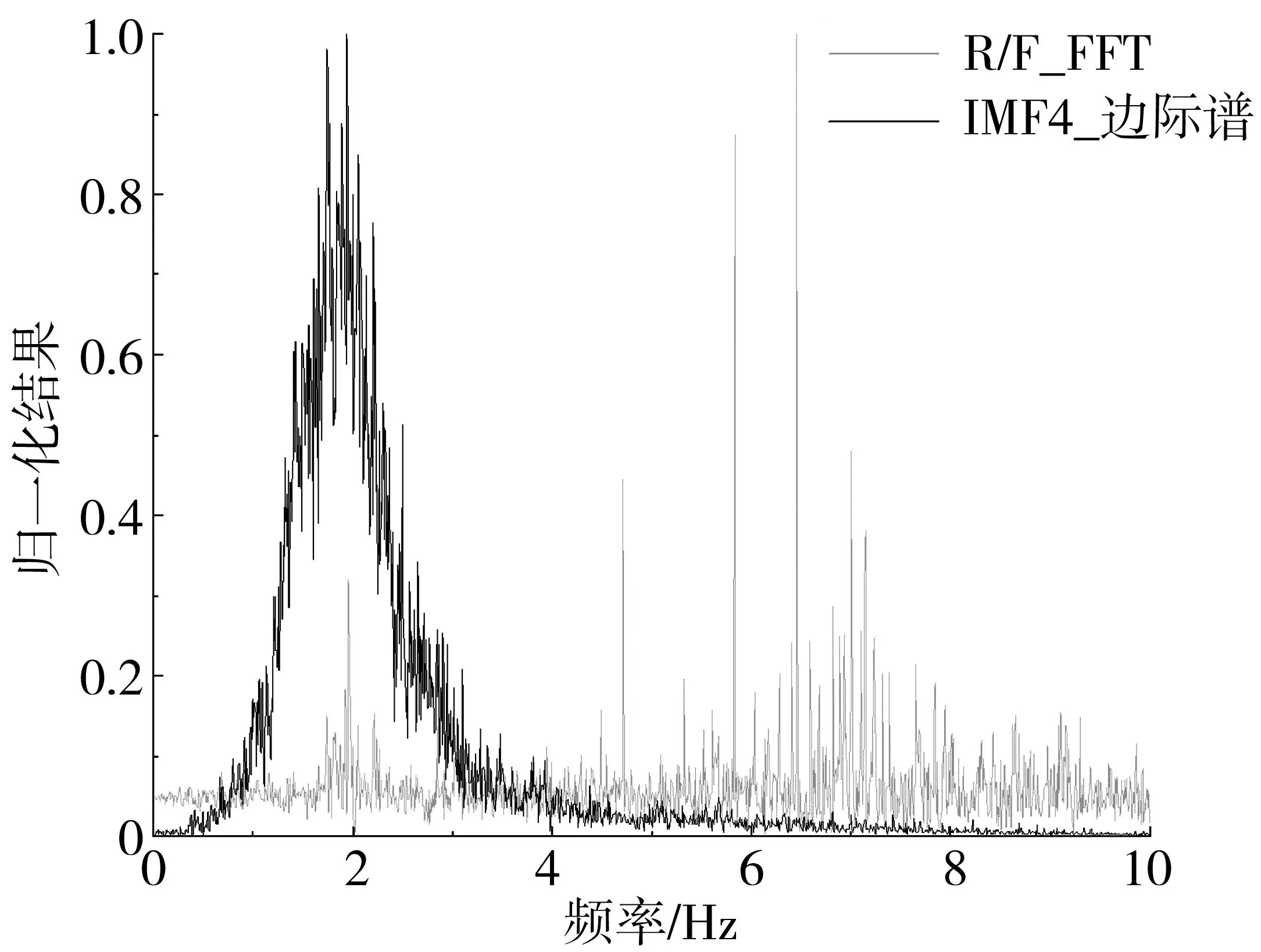
图10 归一化后的R/F谱比计算结果和IMF4的边际谱计算结果Fig.10 Normalized R/F spectral ratio calculation results and IMF4 marginal spectrum calculation results
对该小区共计7栋建筑分别实测3次,从时域脉动数据中截取相同的时间长度,利用FFT、R/F谱比、HHT 3种方法,获取结构基本自振周期,最后取3次测试结果的平均值,得到表1所示的结果。由表1可见,3种方法得到的建筑结构自振周期基本一致。在读取的难易程度上,R/F谱比方法有时会让信号较强的频率峰值显著放大,会让“第一个峰值”淹没于众多峰值中,反而难以识别,HHT发挥比较稳定,优于其他两种方法。
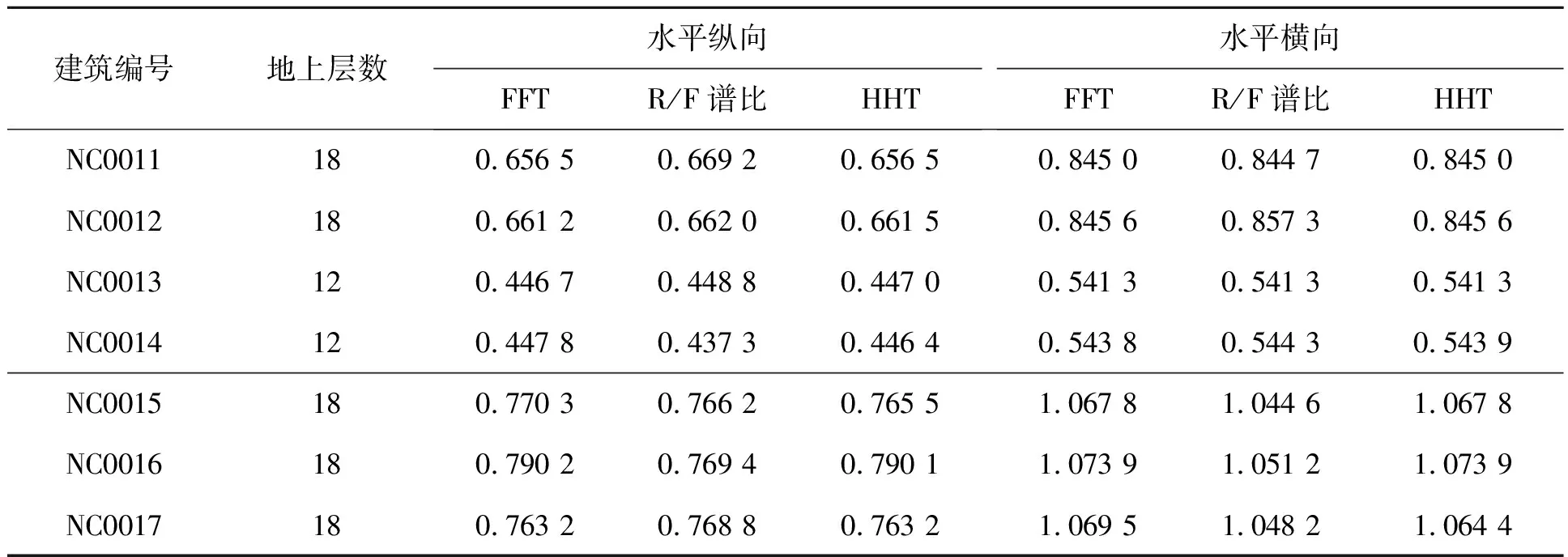
表1 3种分析方法计算结果对比Tab.1 Comparison of calculation results of three analytical methods
4 结论
1) 由于住宅在白天会存在较强的人为振动干扰,结构脉动信号的功率谱存在多个峰值,能量分散,主峰不明显,高频处具有较高的能量,结构基本自振周期难以识别。
2) R/F谱比法基于成熟的FFT理论,可以在一定程度上改善信号的基线漂移,继而获取建筑结构基本自振周期,具有一定的研究意义。但其需要用更长的缆线连接设备,实现两个测点同时测量的要求,尤其是对于高层或者超高层建筑的测量多有不便。
3) EMD可将富含干扰信号分解为若干个不同的本征模态函数(IMF)和一个余项。其中各个不同的本征模态函数反映了信号的局部特性,残余量反映了信号的趋势或均值。EMD通过“筛选”的方法把残余量分离出来,明显改善因基线漂移造成的波形畸变。
4) 利用EMD从原始信号中获取若干个信号分量,然后通过Hilbert变换和积分获得边际谱,或者直接对各信号分量进行FFT获得功率谱,从这两种图谱中都能获得较好结果。HHT方法显著提高了实测效率和分析的准确性,适合用于建筑结构基本自振周期快速、大规模和自动化识别。
