桂西桂北地区杉木高生长模型研究

黄敬业

广西华森设计咨询有限公司，广西 南宁 530011

0 引言

杉木是我国南方主要的用材林树种之一。古代杉木的分布较为广泛，东至江浙一带，西至四川省、贵州省、湖北省交界处，北至大别山北部，南至广西壮族自治区（以下简称广西）、广东省北部南岭山地［1］。广西是我国杉木中心产区之一，杉木栽培历史悠久、遗传基础单一［2］。广西14 个设区市均有杉木分布，其中桂北、桂西北、桂东北为中心产区，桂东、桂中和桂西北部分地区为一般产区，桂东南、桂西南和桂南部分地区为边缘产区。其中，桂北的融水苗族自治县、三江侗族自治县、融安县等（广西杉木的中亚热带中心产区）生产的杉木品质最优，而且融水苗族自治县、三江侗族自治县等是广西重要的杉木良种苗木繁育示范基地［3-5］。杉木是广西三大重要的用材林树种之一，2020 年其种植面积为189.48 万hm2，占广西森林植被面积的12.9%；蓄积量达19 713.38万m3，占全区乔木林树种蓄积量的21.2%。研究杉木的高生长模型，有利于指导杉木生产，也有助于掌握杉木资源的消长变化情况。

1 研究材料与方法

1.1 材料获取

此次研究材料来自广西2015 年森林资源连续清查数据。全区的样地数量是4 946 个，杉木样地（杉木样地株数大于等于88株才统计）数量是161个，其中桂西、桂北地区的杉木样地数量是134 个。经数据处理，剔除异常值后，保留杉木样地数量112个。

1.2 研究方法

1.2.1 数据处理

第一步是按杉木树龄从小到大排列树高数据；第二步是按1.5 个标准差剔除杉木样地每个龄阶的异常树高数据；第三步是对新的树高数据总体按1.5个标准差剔除异常树高数据，保留了112 个杉木样地数据；第四步是按龄阶从小到大排序，取各龄阶树高均值，最终获得17组龄阶—树高数据（见表1）。

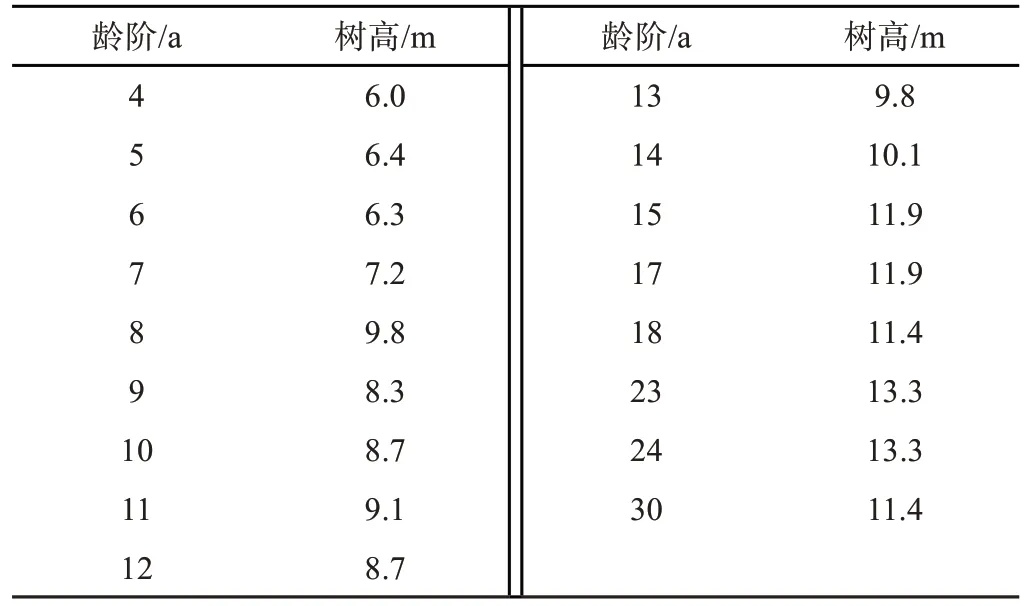
表1 桂西桂北地区杉木龄阶—树高

1.2.2 建立模型

描述林木的生长变化有大量的公式和曲线，总体上可分为两大类：一类是经验方程，另一类是理论方程。经验方程缺乏生物学假设，模型中的参数无任何生物学意义，逻辑性和普适性较差，仅适合描述观测的数据及数据范围，很难进行外延和推广应用；理论生长方程根据生物学特性作出假设，建立林木生长曲线方程，与经验方程相比，逻辑性强，适用性广，参数可作出生物学解释，对未来趋势可以进行预测［6］。以下选取Logistic、Compertz、Richards、Hossfeld Ⅳ等备选方程来拟合桂西桂北的杉木树高生长模型（见表2），再择优选择。

表2 林木生长拟合中常用的理论生长方程

1.2.3 评价指标

树高生长模型的适应性，主要看其拟合好坏，通过决定系数R2、均方误差（Mean Square Error，MSE）、估计值的标准差（Standard Error of Estimate，SEE）、平均预估误差（Mean Prediction Error，MPE）、总相对误差（Total Relative Error，TRE）等指标进行模型评价。此次采用ForStat30 和SPSS19.0 软件进行拟合分析。

2 研究结果与分析

2.1 树高方程拟合初值

利用ForStat30 对桂西桂北地区杉木数据进行拟合，得到杉木高生长拟合模型的参数初值和方程相关系数，具体如表3所示。杉木高生长拟合模型为

表3 杉木树高生长拟合模型

模型1 Logistic：H= 12.424/（1 + 2.426e-0.190t）

模型2 Compertz：H= 13.377e-1.370e-0.123t

模型3 Richards：H= 14.305/（1 - e-0.067t）0.644

模型4 Hossfeld Ⅳ：H= 13.005/（1 + 9.889/t1.415）

2.2 模型回归分析

利用SPSS19.0对上述4个模型和参数初值进行非线性回归分析，根据最小二乘法原则，采用麦夸尔特法（Levenberg-Marquardt）迭代计算出模型参数，得到以下回归方程。

模型1 Logistic：H= 13.008/（1 + 2.444e-0.169t），MSE=0.751，R2=0.881

模型2 Compertz：H= 13.217e-1.430e-0.132t，MSE=0.779，R2=0.876

模型3 Richards：H= 13.624/（1 - e-0.089t）0.762，MSE=0.832，R2=0.868

模型4 Hossfeld Ⅳ：H= 16.521/（1 + 8.294/t1.011），MSE=0.874，R2=0.861

上述回归方程的决定系数R2的大小排序为模型1>模型2>模型3>模型4，决定系数R2越接近1，则回归方程变量的相关性越高，一般认为R2的绝对值在0.8以上为强相关性，4 个回归方程的相关性都达到强相关，其中以模型1的回归方程相关性最高，其次是模型2，具体见表4。回归方程均方误差MSE大小排序为模型1（0.751）<模型2（0.779）<模型3（0.832）<模型4（0.874），模型1的均方误差最小，具体见表4。MSE越小，则回归方程与实测值之间的误差越小，回归方程拟合度越好。

表4 方差分析

回归方程参数估计值的标准误与95%置信区间相联反映出参数估计值取值的随机误差大小，标准误越小、置信区间间隔越窄，则随机误差越小，模型参数估计值结果越精准。由表5可知，3个参数中，a估计值的标准误差大小排序为模型1<模型2<模型3<模型4，b估计值标准误差大小排序为模型1<模型3<模型2<模型4，c估计值标准误差大小排序为模型2<模型1<模型3<模型4。参数a估计值95%精度置信区间间隔大小为模型1<模型2<模型3<模型4，参数b估计值95%精度置信区间间隔大小为模型2<模型3<模型1<模型4，参数c估计值95%精度置信区间间隔大小为模型2<模型1<模型3<模型4。回归方程的参数中以a、c参数为重，分别确定生长模型曲线的最大值渐近线和最高生长速度的转折节点，经两个参数估计值的标准误和95%精度置信区间间隔大小的比较分析，得出模型1和模型2的参数估计值随机误差较小，其次是模型3，模型4则较差。

表5 回归方程参数估计

模型H估计值的标准差SEE和变异系数Cv越小，数据的离散度越小，模型的稳定性越好。一般认为，Cv大于10%时容易脱离实际或应慎用［7-8］。由表6 可知，模型统计量H的SEE和Cv的大小排序为模型1<模型2<模型3<模型4。4 个回归模型的SEE小于1，且Cv均小于10%，其中模型1 离散度最小，其次为模型2。模型H的平均预估误差MPE、总相对误差TRE指标越小，预估值与实测值之间的误差越小，模型的预测能力越好，是反映模型预估效果优劣的指标。MPE大小排序为模型1<模型2<模型3<模型4；TRE1 大小排序为模型2<模型1<模型3<模型4；TRE2 大小排序为模型2<模型1<模型3<模型4。综合分析发现，模型1 的离散度较小，模型数据的偏差小，模型的预估预测效果更佳、适用性更强，其次是模型2。

表6 统计量及模型评价指标

经过对比分析，模型1 Logistic方程拟合度最优，误差最小，其回归方程为H= 13.008/（1 + 2.444e-0.169t）。该方程反映出桂西桂北地区杉木高生长潜在最大值为13.008 m，潜在生长速率c为0.169（即16.9%）；树高生长方程曲线存在一个生长拐点，即杉木连年生长量达到最大值时，树龄约为5.3 a，树高为6.5 m 时，杉木生长速率最大值为0.549 588（约55.0%）。生长模型反映了桂西桂北地区杉木前期生长较快的特点，尤其以五六年树龄的杉木高生长达到最大值55.0%时，杉木每年可以长高1.2 m。

3 结论

桂西桂北地区杉木的高生长模型最优方程为H=13.008/（1 + 2.444e-0.169t），杉木树高最大值为13.008 m。虽然桂西桂北地区适合杉木生长，但杉木树高最大值为13.008 m，这与桂西桂北地区杉木生产经营较为粗放、抚育管理缺乏有较大关系。因此，有必要改变目前粗放的经营管理方式，增加施肥量，延长抚育期，以提高桂西桂北地区的杉木生产力。在现代森林资源管理方面，可以利用杉木高生长模型与无人机的航测技术、激光雷达技术快速掌握桂西桂北地区杉木资源发展动态，为桂西桂北地区杉木经营生产保驾护航。