一种改进单脉冲技术的低角跟踪性能分析

王安飞, 郭肃丽

(中国电子科技集团 第54研究所，石家庄 050081)

0 引言

当相控阵天线对低仰角目标进行跟踪时，目标发射的经海面或地面反射的信号与直射信号近乎同时被接收。此时的多径反射信号与直射信号是高度相关的，因而从时域、频域上都很难对两者进行分辨[1-3]。

在低仰角环境下，多径效应为影响系统跟踪精度的主要因素。在相控阵系统中，一种同时多波束体制角跟踪方法被广泛应用，即单脉冲技术。在单脉冲体制下，一般通过接收天线的和差波束方向图函数来实现对目标的跟踪测量[4-5]。相控阵系统进行精密角跟踪时通常采用相位和差单脉冲测角技术[6-7]。该方法在多径效应的影响下，测角精度大幅下降，严重时甚至会造成目标丢失。

为了消除多径效应的影响，文献中提出了不同的方法。复角法(CA，complex indicated angles)是最早的有效方法之一；该方法通过单脉冲比的实部和虚部来跟踪低角度目标[8]；文献[9]中提出了一种改进频率分集方法，该方法引用了几个不同的频率和最小平方(LS，least square)算法；文献[10]提出了一种基于频率敏捷的最大似然算法，该方法通过在跟踪过程中调整工作频率，使角度估计的误差最小。在文献[11]中，笔者提出了一种基于CA的自适应混合方法：该方法通过利用改进的CA方法和自适应波束成形算法来抑制多径效应。文献[12]提出了一种基于两种频率的高程几何平均算法：该方法通过利用目标仰角和镜像目标仰角的乘法运算来进行目标跟踪定位。文献[13]介绍了一种双零点(DN, double null)差分模式和固定波束(FB, fixed beam)模式。DN系统能够将目标与镜像目标分离开来，它的差通道有两个指向，其中第二指向在镜像目标方向。几年后，文献[14]通过对DN和FB系统中的和差波束通道进行阵列加权实现了对这两种模式的优化，提出了一种新的具有对称差分模式的单脉冲系统。文献[15]通过数字波束形成技术设计了一种新的对称差波束单脉冲系统，但该系统存在一定的局限性：在理想镜面反射条件下该方法失效。最近。另一种基于FB方法的波束成形技术被提出[16]，该方法能够有效保证波束的均匀对称性。文献[17]提出了一种迭代干扰消除算法来抑制多径效应：基于子空间分解的多信号分类(MUSIC，multiple signal classification)算法[18]，并利用迭代投影理论，通过对每个低仰角目标测量信号的设计，实现了对该方法的性能优化。

相控阵系统中常采用的多径消除技术技术有偏轴单脉冲法、对称波束法。偏轴单脉冲法的指导思想是当目标仰角小于某临界角(一般为0.7倍波束宽度)时，相控阵天线的波束指向不再降低，固定在该方向上[19-20]。由于偏轴跟踪能够抑制出现极端严重多径误差的情况，且实现简单，是一种较常使用的低仰角目标跟踪技术，但该方法的跟踪精度较低。对称波束法通过重新设计接收天线的和、差波束方向图使得单脉冲鉴角曲线关于波束指向偶对称，需要注意的是，该方法要求波束指向目标与镜像目标夹角的角平分线方向。当波束指向与目标-镜像的角平分线重合时，和、差波束单脉冲比仅与直射信号的单脉冲比有关。这时只要我们根据系统的差斜率测出单脉冲比，即可确定目标仰角。但是，由于对称波束法要求目标与其镜像同处于天线波束照射范围内，局限性较大[21-23]。

需要注意的是：多径消除技术的应用有效地提升了单脉冲系统的跟踪精度，但对噪声敏感，且不能够解决信号衰减的问题。空间分集技术的应用能够有效解决这一问题。相控阵系统由于不同阵元放置在不同位置或高度上，空间分集技术的应用可以使得到达这些阵元的反射信号路径不同，从而减少多径效应的影响[24]。常用的空间分集技术有：选择合并分集、等增益合并分集、最大比合并分集。经过理论与实践证明，最大比合并分集(MRC，maximal ratio combining)是一种最佳的空间分集方案[25]。它能够在提高相控阵系统信噪比的同时完成通信系统中断概率的优化，补偿因多径造成的信号衰落，使接收信号功率能够满足跟踪和数据解调要求。

本文提出了一种改进单脉冲测角技术。改进单脉冲技术的处理思想是通过修正天线的方向图消除多径信号的影响。该方法利用相邻脉冲差波束相位跳变构造对称波束，并采用频率分集技术，通过对不同工作频率下得到的和差波束进行一系列运算，能够准确得出目标与镜像目标的角度信息，将特定环境下单脉冲系统的测角误差由之前的1°左右降低到0.1°以下。

1 多径反射模型与机理

1.1 多径反射模型

如图1为相控阵天线与飞行目标所建通信链路的几何模型示意图。设相控阵天线高度为hR，飞行目标高度为hT，反射信号与水平面夹角(λ射余角)为Ψ，等效地球半径为RE，相控阵天线与飞行目标的视线距离为Rd。

根据图1所示的几何关系，可得直射路径与反射路径的路程差△R为：

△R=R1+R2-Rd

(1)

(2)

(3)

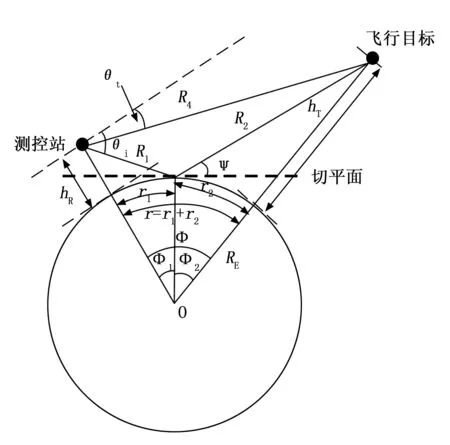
图1 球面反射模型

在该模型下需要计算目标的最大可视距离Llimit。如图2所示，当飞行目标与测控站的距离大于Llimit时，受地球曲面的影响，二者无法建立视距通信链路。

图2 曲面地球模型

由图2中几何关系得：

(4)

假设hR处为一个垂直放置的均匀线阵，阵元数为N，阵元间距为d，工作频率为f，可得波束宽度:

(5)

其中：θe为波束宽度(rad)；k为波束宽度因子，均匀口径照射情况下k通常取值0.886；C为真空中电磁波传播速率，c=3×108m/s；N为阵元个数；d为阵元间距(m)；f为工作频率(Hz)；θ0为波束指向角(rad)。

当反射信号进入相控阵天线波束主瓣反射区时，跟踪精度下降严重，此时直射信号、多径反射信号与波束主瓣宽度的几何关系满足：

θt≤1.5θe

(6)

根据式(5)和图1中几何关系得：

(7)

1.2 多径反射机理

在多径反射中，最主要的一个参数就是反射系数，它决定了多径反射信号相位和幅度上的变化。该系数由菲涅尔反射系数ρ0、扩散因子D、镜面散射因子ρs的乘积组成[26-28]。

ρ=ρ0Dρs

(8)

1.2.1 菲涅尔反射系数

光滑表面的菲涅尔反射系数由反射表面的电磁特性决定，不同极化形式的菲涅尔反射系数表达式如下：

对于垂直极化有:

(9)

对于水平极化有:

(10)

其中：εc是复介电常数：εc=εr-j60λσ，εr为相对介电常数，λ为电磁波的波长，σ为电导率。

表1 不同反射面的电导率和相对介电常数

1.2.2 扩散因子

扩散因子D是考虑地球曲率影响的结果。当反射信号照射到凸起的地球表面时会引起扩散，使得电磁波能量密度衰减。扩散因子的值由下式给出：

(11)

1.2.3 镜面散射因子

反射面的粗糙使得镜面反射的幅度有所衰减，用镜面散射因子ρs表征。它与反射面粗糙度因子Г的关系为：

(12)

ρs随Г的变化曲线如图3所示。

图3 镜面散射因子ρs与粗糙度因子Г的关系曲线

1.3 多径效应下的接收信号模型

在考虑多径效应的情况下，假设反射面为平静海面，则相控阵天线接收信号电平F表示为：

F=|g(θ1)+ρg(θ2)e-jφ|

(13)

这里θ1、θ2分别为波束指向与目标、目标镜像的夹角，φ是由目标上电磁波传播的直射与反射路径之间的路程差△R引起的相对相位差：

(14)

其中：λ为信号波长，△R随目标距离的变化而相应地发生变化。图4给出了多径效应下相控阵天线接收信号电平F(对数表示)随视线距离Rd的变化情况，可以看出多径效应的影响相当越严重。

图4 多径效应影响下的方向图传播因子ht=2 km， hr=5 m，载波频率fc=6 GHz

2 多径对低角跟踪的影响

在单脉冲体制下，相控阵系统一般通过接收天线的和、差波束方向图函数实现对目标的跟踪测量。当相控阵天线高度为米级，目标飞行高度为公里级，距离相控阵天线的视线距离公里级时，球面反射模型可简化为如图5所示的理想平面反射模型。假设θ0表示波束指向，△θ表示波束指向偏差，和波束方向图函数为F∑(θ+△θ)，差波束方向图函数为FΔ(θ+Δθ)，经过跟踪接收机的信号接收后产生角误差电压驱动，和波束不断向最大值方向移动，差波束不断向方向图为零的方向移动，进而实现对目标的实时跟踪。

图5 理想平面反射模型示意图

假设只考虑镜面反射的影响，当阵列天线的波束中心指向水平方向时，系统的和信号和差信号分别为：

V∑=F∑(θt)+ρF∑(θi)

(15)

VΔ=FΔ(θt)+ρFΔ(θi)

(16)

式中，θt为目标仰角；θi为镜像目标仰角；ρ为反射系数。根据图4，在低仰角环境下，可近似认为，Δθ≈0，θt=-θi=θ。由此得到和差波束单脉冲比为：

(17)

由于和波束方向图函数为偶函数，差波束方向图函数为奇函数，即：

(18)

因此：

(19)

式(19)表明，多径条件下经典单脉冲系统的单脉冲比与目标仰角、反射系数有关。当反射系数未知时，无法根据单脉冲比准确求出目标仰角。

如图6为理想条件与多径效应影响下的和差波束方向图。在该实验中，设定垂直地面放置的均匀线阵阵元数为16，测控站高度为5 m，目标飞行高度为200 m，视线距离为10 km。从图中我们可以得出，受多径效应的影响，和波束对称轴、差波束对称中心发生偏移，差零深降低。这时即使波束指向偏差为零，角误差信号也不为零，若要使角误差信号为0，则必须将波束指向另外偏转一个角度使其与多径反射信号相抵消。这个另外偏转的角，就是多径效应形成的测角误差。

图6 理想条件与多径效应影响下和差波束方向图

如果对该单脉冲算法进行改进，使得和差波束单脉冲鉴角曲线关于波束指向偶对称，即：

(20)

代入式(17)可得：

(21)

此时，和、差波束单脉冲比仅与直射信号的单脉冲比有关，而与多径反射信号无关，多径反射信号分量在测角过程中被完全抵消了。因此，改进单脉冲测角法能够有效克服多径对于单脉冲比的影响。

3 改进单脉冲测角技术原理与功能实现

在该单脉冲体制下，相控阵系统假设目标的运动状态在相邻脉冲周期内基本保持不变，测控站选用垂直均匀线阵，阵元数为2N，如果在第k个脉冲时刻相控阵天线发射波束指向目标，则在第k+1个脉冲时刻相控阵系统切换工作模式，通过控制数字移相器使发射波束指向镜像目标。然后在第k+2个脉冲时刻波束指向目标，第k+3个脉冲时刻指向镜像目标，依此不断循环往复。则在第k个脉冲时刻内波束扫描到的来自目标的直射信号和来自镜像目标的反射信号可表示为：

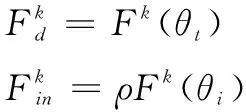
(22)

第k+1个脉冲时刻内波束扫描到的来自目标的直射信号和来自镜像目标的反射信号可表示为：

(23)

(24)

在单脉冲系统中，由第k个和第k+1个相邻脉冲时刻波束扫描信号组成的和信号可表示为：

(25)

由上、下子阵波束扫描信号组成的差信号可表示为：

(26)

改进单脉冲系统的和差波束形成网络如图7所示。

图7 改进单脉冲测角法和差波束形成网络

根据相控阵系统的单脉冲测角原理可知，该情况下得到的和差波束单脉冲比与反射系数ρ有关，无法准确得出目标仰角。为了消除反射系数ρ，这里拟采用频率分集的方式：假设目标发射f1、f2两种不同工作频率的信号，在相控阵系统接收端同时接收这两个信号后合成。当相控阵天线采用不同的工作频率f1、f2时，根据图8我们可以到不同频率下的和、差信号功率为：

图8 直射信号与反射信号的合成

(27)

(28)

(29)

(30)

当频率变化较小时，可近似认为|ρf1|=|ρf2|。通过运用几何平均算法，将不同工作频率下和差信号进行如下运算得到的和差波束单脉冲比T1与反射系数ρ无关，计算结果如下：

(31)

由单脉冲测角原理可知：

(32)

(33)

其中:k为差斜率。将式(32)～(33)联立可得：

T1=k2θtθi

(34)

在镜像多径对称条件下可近似认为θt=-θi，则式(34)可表示为：

T1=-k2θt

(35)

因此，根据T1查表即可近似得到目标仰角θt。(相控阵系统的差斜率已知)根据式(34)、(35)可知，该计算存在一个近似，而实际上有几何关系可知，目标仰角θt是略小于镜像目标仰角θi的。因此，仅由T1不能够准确计算出θt和θi。

根据式(34)可知，由T1得出了θt和θi的积，若要进一步提升单脉冲系统的跟踪精度，实现目标与镜像的分离，可将不同频率的和、差信号进行如下运算得到T2：

(36)

将式(32)、(33)代入式(36)可得：

(37)

根据式(37)可知，由T2得出了θt和θi的和，利用平方和差公式与式(35)联立，θt可以准确计算出目标仰角θt与镜像目标仰角θt的值，有效克服了系统误差对系统跟踪性能的影响：

(38)

(39)

在某些频段内，受附加噪声的影响和信号输出功率|∑f1|2、|∑f2|2的差值很小，导致改进单脉冲法的性能恶化。因此，需要对频率f1、f2，使得和信号输出功率的差值最大。由式(27)、(28)可得：

|∑f1|2-|∑f2|2=2∑d∑inρ(cos(φf1)-cos(φf2))

(40)

经化简可得:

(41)

4 空间分集——最大比合并分集在相控阵系统中的应用

在低仰角情况下，由于直射信号与反射信号的干涉，多径效应不仅会造成相控阵天线俯仰方向差方向图零点偏移，跟踪精度降低，还会造成信号衰落，影响数据的接收和解调。改进单脉冲测角技术方法消除了多径带来的测角误差，但为了保证相控阵系统跟踪性能的稳定性，还必须设法补偿多径造成的信号衰落，使接收信号功率足以满足跟踪和数据解调要求。

假设实验场景为平静海面，载波频率为6 GHz，目标在200 m高度定高飞行。由于反射信号到达各接收天线路径不同，使它们接收的信号不同时处于零点，至少有一个天线会收到较强的信号，从而减少了多径衰落的影响。根据图9，当天线处于不同高度(10、15、20 m)时，或天线处于同一高度而工作在不同视线距离时，其接收信号都不同时处于谷点。这时空间分集是解决多径衰落问题的最佳方案。如果使用两个空间分离的天线来接收遥测信号，问题就变成了如何放置天线，以便当一个天线处于无效状态时，另一个天线处于峰值状态。然后，将这些接收信号进行适当组合，就会使合成接收信号增强，减少多径衰落的影响。

图9 不同视线距离下接收信号强度随接收 天线高度的变化曲线

空间分集技术的应用可以使得到达这些阵元的反射信号路径不同，从而减少多径效应的影响，然后通过计算机软件仿真和现场实验分析，我们可以得出每个特定多径场景下的最佳空间分集距离，从而为相控阵系统阵间距离参数的设置提供参考。

常用的空间分集技术有：选择合并分集、等增益合并分集、最大比合并分集。经过理论与实践证明，MRC分集是一种最佳的空间分集方案。它在提高分系统信噪比的同时完成了对于通信系统中断概率优化。

最大比合并的实现方式即通过给分集的N路不同信号乘以一个不同的系数ωi，i=1,2,3,…,N。如图10所示，相控阵系统接收端采用MRC分集来优化处理来自N个分集支路信道的接收信号，假设各支路信号独立衰落且服从瑞利衰落分布。

图10 相控阵系统MRC分集接收机模型

假设第i支路接收信号表示为：

yi(t)=gi(t)s(t)+n(t)

(42)

其中:yi(t)是传输的信号，gi(t)是第i个支路上的衰落增益，n(t)是第i个支路上的噪声。

其中各支路信号是同相的，在进入分集合路器之前需要乘以一个加权系数ωi(等于各支路信号幅度与噪声功率之比)。

4.1 瑞利衰落信道的中断概率

情况一：设x1，x2，…，xn为n个独立服从指数分布的随机变量：

fxi(xi)=βiexp(-βixi),xi>0

(43)

假设参数βi(i=1,2,3,…)都是不同的，则Sn=x1+x2+…+xn的概率分布函数：

(44)

情况二：设x1，x2，…，xn为n个独立服从指数分布的随机变量，不要求参数βi(i=1,2,3,…,N)都是不同的，假设其中有r个不同的参数1

(45)

其中：ki(i=1,…,r)表示MRC各分集支路功率中与βi(i=1,…,r)具有相同功率的支路数。

4.2 瑞利信道MRC分集各支路平均信噪比的概率

密度函数(PDF,probability density function)

(46)

其中：N表示MRC分集的分支数，p1表示情况一功率的符号。

(47)

其中：p2表示情况二功率的符号。

图11为(情况二)四支路MRC分集在瑞利衰落信道下的PDF与信噪比γ的关系，表2给出了4个不等功率瑞利分支的平均信噪比。

图11 四支路MRC分集在瑞利衰落信道下的 理论与实际PDF与信噪比γ的关系

表2 四个瑞利衰落分支下的平均信噪比γdB

图11中的仿真结果显示与理论结果完全一致。从图中观察可以得出表2给出的四个瑞利分支下的平均信噪比对应的MRC分集合路输出信噪比主要集中在5～35 dB。

5 系统性能分析

研究采用Matlab软件进行低仰角跟踪算法的仿真与分析，采用目标仰角下单脉冲测角的最小均方根误差(RMS，root mean square)性能作为低角跟踪算法的评判标准。假设试验场景为平静海面，垂直地面放置的均匀线阵阵元数为16，测控站高度为5 m，目标飞行高度为5 km，SNR=15 dB,发射信号中心频率为f0=5 GHz，相对带宽BW=20%。假设f1=4.5 GHz,根据式(41)可以计算出该频段内输出功率差值最大时对应的频率f2=4.9 GHz。

则当f1=4.5 GHz,f2=4.9 GHz时，改进单脉冲测角法与采用中心频率f0=5 GHz的传统单脉冲测角法的跟踪性能对比如图12所示。根据图中结果可以看出：在低仰角环境下(θt<3°时)传统单脉冲测角法的测角误差在1.5°左右，相控阵系统的无法实现目标的准确跟踪。对比传统单脉冲测角法，改进单脉冲测角法的测角误差由之前的1°左右降低到0.1°以下，系统的跟踪性能明显提高。综上所述，改进单脉冲测角技术的应用实现了相控阵系统对于低仰角目标的稳定精密跟踪，具有良好的工程实用价值。

图12 系统改善前后跟踪性能对比

6 结束语

介绍了多径效应模型与机理，分析了多径效应对于单脉冲系统低仰角跟踪性能的影响及传统单脉冲测角技术的局限性，并根据这一问题提出了利用相邻差波束相位跳变构造对称波束的改进单脉冲测角技术。结合理论分析与仿真结果可以发现，改进单脉冲测角技术能够有效克服多径效应对单脉冲系统跟踪精度的影响，并且跟踪精度改善效果明显。由于低仰角环境下镜面反射信号、漫反射信号进入相控阵天线波束主瓣，系统测得的角误差电压会受到来自于镜像目标的干扰，严重影响跟踪精度。因此，解决低角跟踪问题的关键在于将目标与镜像目标区分开来。本文利用飞行目标在相控阵系统接受端相邻脉冲采样时刻内运动状态保持不变的特性，控制数字移相器实现差波束相跳变构造对称波束，并引入频率分级技术，通过对和波束、差波束及其单脉冲比的运算巧妙地将直射和波束、直射差波束、反射和波束、反射差波束分离开来，从而准确测得目标的角度信息。但是改进单脉冲测角技术方法的测角精度受频段选择与信噪比的影响较大，因而在实际工程应用当中需要对此进行严格甄选。