基于正弦数据压缩算法的DDS研究及FPGA实现

闵令辉，曹晓东，程 凯，王 哲

(1.聊城大学 山东省光通信科学与技术重点实验室,山东 聊城 252000；2.中国科学院大学 高速电路与神经网络实验室, 北京 100049；3.中国科院 半导体研究所, 北京 100083)

0 引言

频率合成技术(DDS，direct digital synthesis)由美国学者于1971年基于相位转换概念出发首次提出[1]。近年来随着数字技术的发展以及器件制作工艺水平的提高，直接数字频率合成器(DDS)技术也越来越成熟，它在很多的性能方面都远远超过了以前传统的频率集成合成器。比如说它的工作频率范围比传统的要广，在设计上频率的转换速度比传统的快，频率的分辨能力也比传统的强，相位的连续性比传统的要好，正交输出参数比传统的精度高等等。光具备以上的性能优势还并不够，接着Garvey等人为了能更好地挖掘出DDS的优点于是对DDS的组成结构以及工作时的频谱特性进行更加深入的研究。为了能对传统频率合成技术的缺点进行完善和克服所以选择完全采用数字技术来进行频率合成，同时是因为从相位的概念出发所以频率合成技术具有高频率分辨率、高稳定性、易操控、转换频率快等优点[2-3]。DDS要实现高精度的输出必然要占据很大的内存空间，数据转换时，数据量大，处理速度受到限制。

基于以上问题文献[4]提出了一种在不使用ROM的情况下将贝塞尔曲线进行5次迭代的方式合成正弦信号的设计，但设计较为繁琐，电路结构复杂。文献[5]使用CORDIC算法来获取对应的正玄波，其获取的方式以及角度主要是通过上一次的迭代的角度来确定下一次的迭代方向，精度越高，迭代次数越多，速度就越慢。文献[7]使用sunderland算法将相位累加器的输出分成高位、中间位和低位，读取两个存储正弦波幅度值的查找表后相加作为输出，压缩比为1:42.6。

与以上不同的是，本论文提出了一种将改进sunderland算法与QE-ROM算法相结合的正弦数据压缩方法，在不改变波形输出精度的前提下，对全周期的正弦波数据进行压缩从而达到降低ROM存储空间开销的的目的。通过对整体设计进行建模仿真验证了设计的正确性，并利用FPGA进行了硬件电路的实现。

1 DDS工作原理

DDS指的是数字频率合成技术，其更深层次的含义则是从相位的角度来对波形进行合成。它的硬件电路设计主要包括有基准时钟模块设计，内部的频率累加器设计，波形相位累加器设计，波形幅度与相位相互转换的模块电路设计，数模转换器模块电路设计，低通滤波器设计以及其他外围硬件等等。要想获取到DDS的输出信号频率则需要得到相位累加器的溢出频率即可。但是要想相位累加器出现溢出则需要在时钟fclk信号的辅助下将数据加法器输入端的频率控制字信号Fword进行线性相位的叠加直至产生溢出为止。如图1所示，其中相位累加器包括一个N位频率寄存器，该频率寄存器存储频率控制字Δφ，全加器和相位寄存器分别用于累加和保存累加后的数据。N位的频率控制字在每个时钟周期被执行一次累加。频率控制字表示相角步长，得到线性循环增长的相位值。输出频率由式(1)表示：

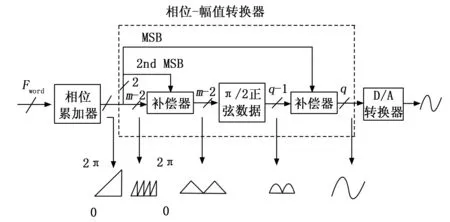
图1 全周期正弦数据重建过程

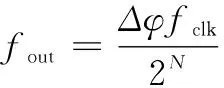
(1)

其中:N为相位累加器的位宽，Δφ为频率控制字，fclk为系统时钟，fout为输出频率。x相位-幅值转换器将相位信息转换为正弦波的幅度值[6]。在相位精度无穷大且无幅值量化的理想情况下，它的输出序列由式(2)确定：

(2)

其中:φ(n)为相位累加寄存器在第n个周期的值，相位累加器输出序列的数字周期定义为T的最小值，对于所有的n存在φ(n)=φ(n+T)，相位累加器输出序列的数字周期为:

(3)

GCD(Pword,2N)为Pword与2N间的最大公约数，当为2的整数次幂时，相位截断后锯齿波的周期等于理想化连续时间锯齿波的周期。ROM的输出被送到D/A转换器，它产生一个量化的模拟正弦波。

一个16位输出的DDS所使用ROM的尺寸为2B×M，其中B是被截断的相位地址的字长，M是ROM的字长。若希望提高ROM的分辨率，则需要更大的ROM存储，这就意味着更高的功耗、更低的速度和更大的成本，所以对ROM尺寸的精简就显得尤为重要。

2 ROM压缩算法对比分析

2.1 Sunderland算法

其本质为利用和积化差公式将sin(α+β+γ)等效成sin(α+β)cos(γ)+cos(α)cos(β)sin(γ)-cos(α)sin(β)cos(γ)通过两个更小的存储单元coarse ROM与fine ROM，大小为2α+β和2α+γ来代替原来大小为2α+β+γ的ROM，其中α、β、γ分别为想正弦函数相位的最高位、中间为和最低位[7]。因为α远大于β和γ所以原始又可化简为sin(α+β+γ)≈sin(α+β)+cos(α)sin(γ)。

为了进一步对ROM进行缩小处理，其中可以通过常规的方式来进行，将上述的方程式分成粗略的ROM和精确的ROM两个部分来完成存储，这样可以达到缩小ROM空间的目的，但是此种方式还需要添加一个加法器将两部分的结果相加并进行重组才能获取到新的正弦函数。除此之外Nicholas 等人还对上述的方式进行了改进，利用计算机技术中的近似算法来代替三角函数近似法最终实现缩减ROM的目的[7]。

2.2 基于泰勒级数的线性插值法

Bellaouar提出的新型的映射技术方法是基于泰勒级数的线性插值法。其主要的原理就是在变换的过程中可以通过查表法将相位值转换成幅度值sin(θ)[8]。这种方法在正弦函数四分之一周期对称性的基础上，同时采用了线性插值法。在coarse ROM中每一个(xi,xi+1)范围内正弦函数可以用式(4)表示：

sin(θ)=sin(θi)+α(t-ti)+δsin

(4)

其中:θ=2πφ/2M；xi和xi+1是粗略ROM中的连续相位；t-ti代表累加输出，同时t表示的是ROM地址的低有效位，ti表示的是 ROM地址的高有效位；α表示的是ROM 表内的正弦函数插值系数。在式(4)中,δsin是正弦函数的泰勒展开式余项[8]。其可定义如下：

(5)

巳知相位幅度转换输出的幅度值为:

f(x)=Asin(πx/2)-ε(x),0≤x≤1

(6)

其中:A的幅度值≤ε(x)是近似误差[8]。假设正弦信号的幅度值是Lbit。为了能获取到最大的输出幅度值则需要选择最优的幅度系数A。一般A取(2L-1)/2L。在此基础上要想完成相位与幅度之间的转换则线性插值法的表达等式如式(7)所示，其中f(x)为幅度值的输出:

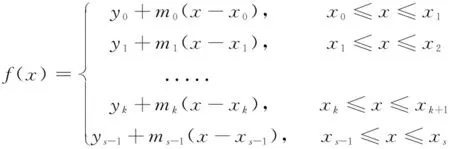
(7)

其中:s为分段的个数，mk和表示的是斜率值，yk表示的是初始的幅度值；xk是表示的是每个阶段的下限值。若要想将上式进行最大的简化则需要挑选合适的分段个数以及长度才能实现。若分段个数的权值取值为2，则分段个数的最高有效位log2s其表示分段个数的值为k，同时通过查表得到所存储的斜率系数的原始幅度值进行寻址。

2.3 存储增量压缩算法

文献[9]通过验证奈奎斯特采样定理当正弦曲线满足方程y=a×sin(ωt+φ)+c即可得到一组离散序列:

yi=a×sin(ωt+φ)+c,i=0,1，...，4095

(8)

峰峰值2a=212-1，角频率ω=2π，采样间隔ti+1-ti=1/(212-1),由此可以计算幅度序列相对增量的绝对值:

|yi+1-yi|=|[a×sin(ωti+1+φ)+c]|-

[a×sin(ωti+φ)+c]

(9)

可以得出，当输出精度是12位且采集幅度序列的相位为212时，在一个采样周期内幅度序列的相对增量其绝对值≤4，此时的存储空间仅仅需要3 bit即可，这相比与以前传统的存储方式缩减了原有空间的75%，在这样的情况下则出现了一种ROM的新型压缩方法。这种方法的主要目的就是可以还原出正弦波的真实幅度序列，同时为了更进一步地压缩存储空间，可以采用单象限幅度序列存储结合反相器最终获取到完整的正弦波形，这样的操作方式还能更好地节约硬件资源。

2.4 ROM压缩算法分析

由上述讨论可知，DDS输出信号的频谱纯度取决于储存在正弦波查找表ROM中数值的分辨率，因此只有增加ROM的分辨率才能提高频谱纯度[10-11]。然而大的ROM意味着较高的功耗、较低的速度和昂贵的成本，为此需要有精确算法的压缩技术。王晓音在实现DDS的波形存储表幅度值压缩方法一文中提到：为了改善DDS的输出频谱主要是通过增大ROM表的寻址空间同时对幅度表进行压缩来实现。其最终的表现方式是通过减少相位截断位数来改善杂散抑制的功率值。

为了能获取到正弦函数的近似波形，主要采用的是三角函数的恒等变换再加上外部的逻辑控制电路来完成对ROM表的输出进行随机组合。前几节列出的几种方法中，1/4周期表、Sunderland结构和Nicholas优化方法都会引入有限的算法误差。其中较为简单的结构方法是Sunderland粗细表，它虽然简单但是它的杂散抑制水平还是相对较好的；Nicholas优化方法相对于Sunderland结构来说其杂散抑制水平更高，同时其还具有非常好的压缩比；基于改进的正弦-相位差法与Nicholas优化方法具有同样的杂散抑制水平，并进一步提高了压缩比。

存储相对增量的ROM压缩算法可以生成包括正弦波、方波在内的多种波形但整体压缩比为27：1，还有一定的提升空间。基于泰勒级数的线性插值算法与线性插值算法都有比sunderland算法更高的压缩比但是在电路补偿结构中使用了乘法器，很大程度上增加了电路路资源的使用，且逻辑控制过于复杂，实时性相对来差了一些。若在设计的过程中做到幅度表压缩节约的资源比提高压缩比所占用的电路设计资源还要多的话则高压缩的追求才会意义重大。论文采用的数据压缩方法是在Sunderland提出的粗细ROM结构压缩结构基础上对粗ROM进一步优化并结QE-ROM技术实现高压缩比的条件下简化电路结构，该结构能够大大降低查找表的存储容量，代价是需要增加能够产生累加器和查表输出的补码逻辑电路。

3 Sunderland 算法优化及性能分析

利用正弦函数的对称性，通过控制相位累加器输出相位值的MSB(最高有效位)和second MSB(次高有效位)即可在只保存(0,π/2)范围内的正弦数据情况下通过两个补偿器重建出全周期的正弦数据。sunderland算法将1/4周期的正弦数据分别放到到两个存储单元分别是coarse ROM 与fine ROM中进行保存。

3.1 改进sunderland算法

sunderland算法在正弦函数1/4对称性质的基础上，将映射sin(θ)的地址位分解成高位α、中间位β和低位γ(本文中α、β、γ依次为5、4、5)。如此sin(π/2(α+β+γ))可表示为：

(10)

四分之一的正弦波幅度值被分别存放在sin(π/2(α+β))所代表的coarse ROM以及cos(π/2(α+β))sin(π/2(γ)所代表的fine ROM。coarse ROM提供了低分辨率的样本，而fine ROM通过在低分辨率样本之间进行插值来提供额外的分辨率。正弦相位差算法(sindiff)利用公式:

max[d(θ)]≈0.21max[sin(θ)]

(11)

在[0,π/8]范围内定义d(θ)的值为m0，代表矩阵为q0则:

m0(alpha_i,beta_i) =A1*2*(2*pi*t0)/pi;

q0(alpha_i,beta_i) = round(m0(alpha_i,beta_i));

其中:alpha_i代表高的地址位α，beta_i代表β。m0随着迭代次数的增加而变化，q0矩阵代表[0,π/2]范围内正弦相位差算法所代表的的幅度值，将其与coarse ROM中的值作差，结果重新保存在coarse ROM中，此时存储的数据为图2中的sindiff。

为了进一步减小保存在coarse ROM中的值引入四线近似算法(QLA)。在[0,π/2]内的函数表达式为：

(12)

用四段函数近似模拟正弦相位差算法后的数据在[0,π/2]范围内的变化曲线，相比于双三角近似算法来说四线近似算法与原曲线有更高的贴合度，误差值也就更小。

以[0,π/8]范围内的数据为例，定义q(θ)为m1，代表矩阵为q1:

m1(alpha_i,beta_i) =A1*((2*pi*t1)/pi);

q1(alpha_i,beta_i) = round(m1(alpha_i,beta_i));

将coarse ROM的原数据依次与正弦相位差(sindiff)算法、四线近似(QLA)算法作差后的误差值重新保存在coarse ROM中，注意此时coarse ROM中存储的数据为图2中的errors而不是原数据。

3.2 QE-ROM算法设计

改进的sunderland算法旨在分割原ROM的地址位并对coarse ROM的数据进行两次幅度值上的压缩，QE-ROM(量化和误差)算法将分别对coarse ROM和fine ROM进行幅度值上的量化，并对量化值与误差值分别存储。

量化过程如图3所示,假设此时的地址位和幅度值分别为A和L，将地址等分为2S段，每个段具有Q位量化值，并且量化值小于该节中的所有数据以使量化误差为正数。Q-ROM大小变成2S×Q位。E-ROM存储量化值与原始数据之间的误差。这些误差比原始数据小得多，因此只需要更小的尺寸。当存储误差所需的位是E时，E-ROM的大小变成2A×e，Q-ROM和E-ROM的总大小变成了2S×Q+2A×e。为了最小化ROM的尺寸，我们必须找到最佳的2S的值，Q-ROM的量化位，以及存储E-ROM所需的位数。具体可以通过以下方法找到：

1)当初始数据的地址位为A，输出为L位时，假设S=A、Q=L。

2)计算每一段的量化值并计算初始数据与量化值之间的误差，得到Q-ROM尺寸。

3)得到可以表示所有误差的E的最小值。

4)计算Q-ROM+E-ROM的大小。

5)减小Q的值然后循环2)～4),如果Q=1则执行6)。

6)减小S的值然后循环2)～5),如果S=1则执行7)。

7)通过比较计算结果得到最合适的Q、S、E使Q-ROM+E-ROM的值最小。

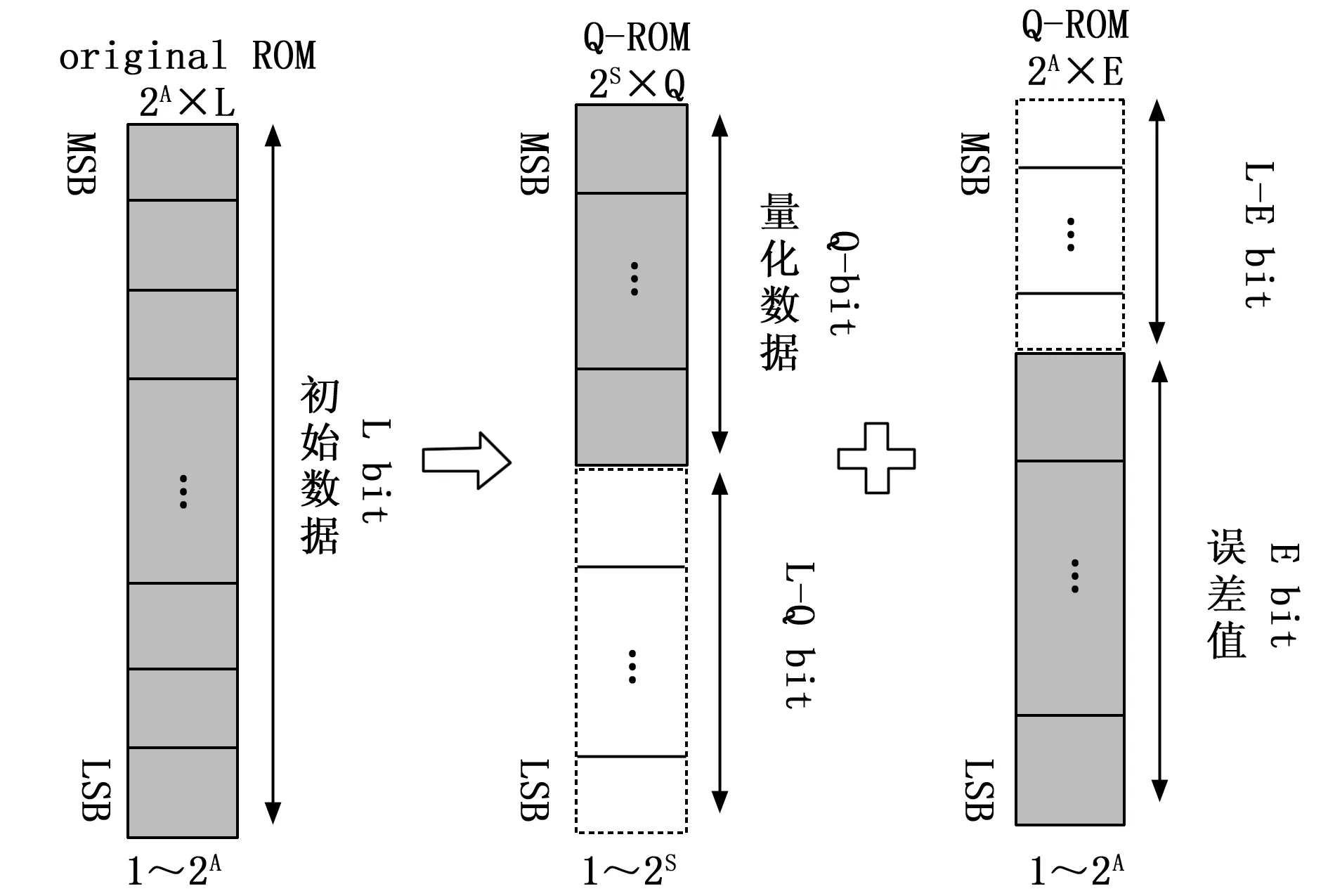
图3 QE_ROM算法量化过程

3.3 性能分析

表1为通过sunderland算法将原始数据分割后各类算法对coarse ROM再压缩的过程和结构。图4为各阶段算法的幅值以及数据总量。

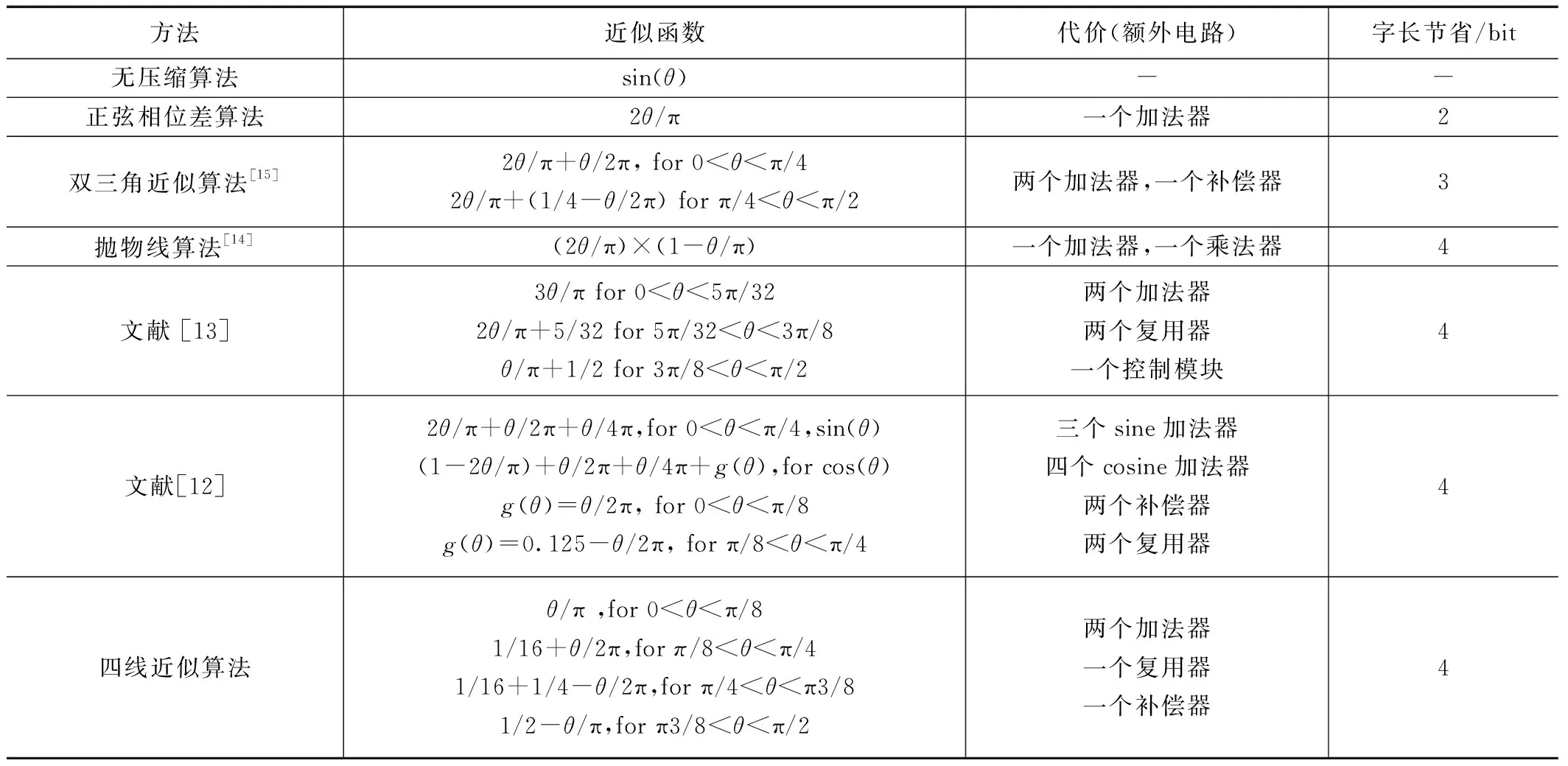
表1 几种正弦压缩算法对比

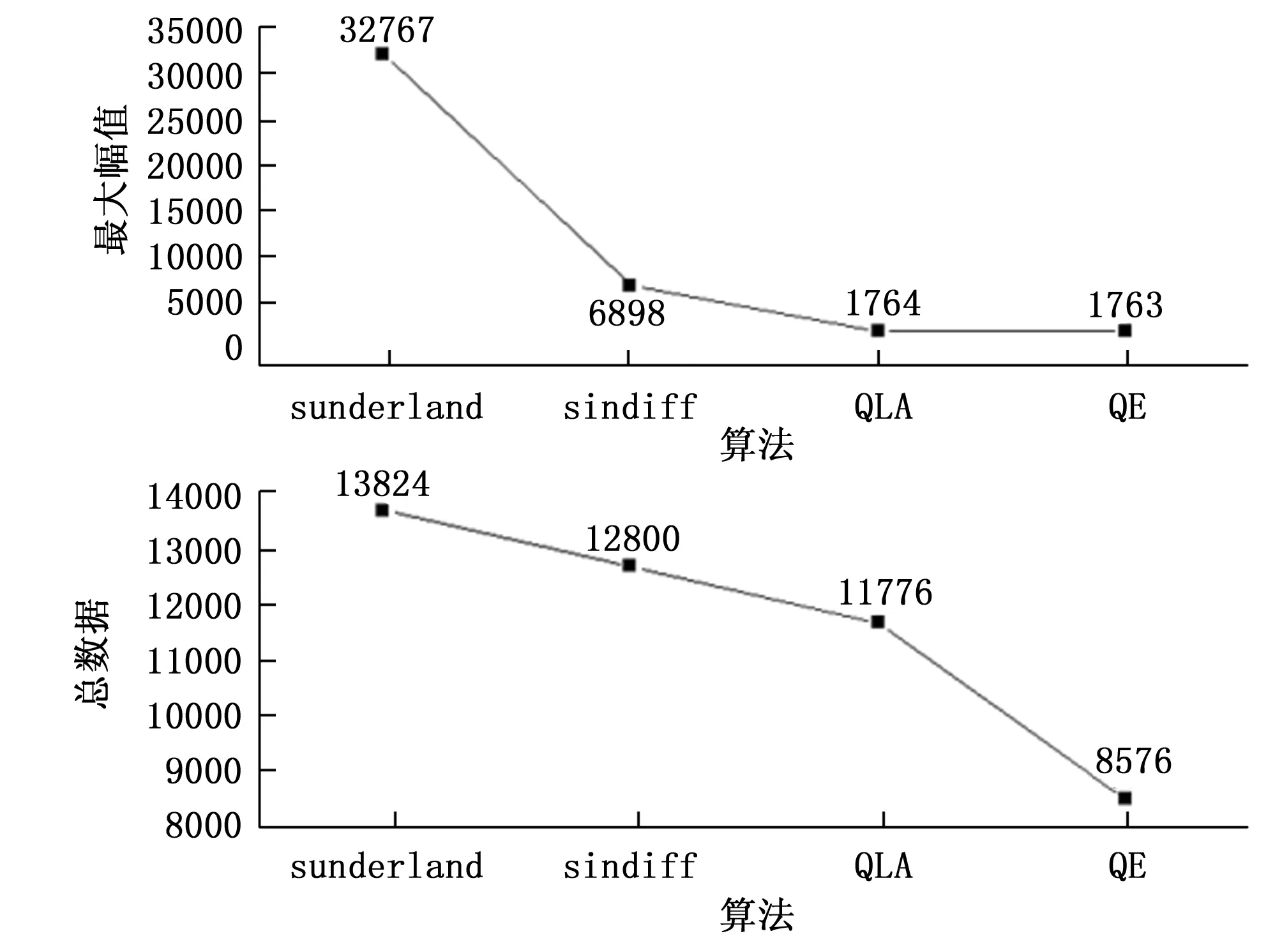
图4 各阶段算法最大幅值与数据量

横坐标中的算法从左往右依次为sunderland算法、正弦相位差算法、四线近似算法、QE-ROM算法。改进后sunderland算法的最大幅度值为1 764，数据总量为11 776 bit，与sunderland算法相比节省了四位字长,ROM面积为原来的85%。

QE-ROM算法以2 bit为步长对幅度值进行量化，然后将量化后的数据与误差值分别存储，结果如图5所示。改进sunderland算法结合QE-ROM算法后的数据总量为8 576 bit，ROM面积为sunderland算法的62%。与压缩前ROM尺寸(216×16)相比，压缩比为122:1。

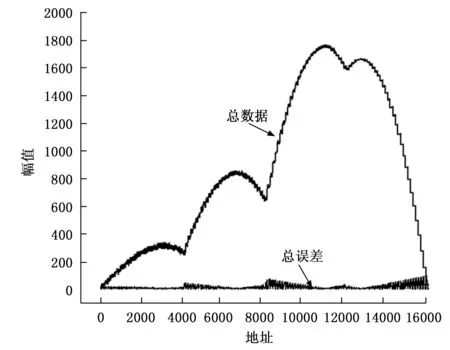
图5 ROM内总数据量

4 基于FPGA的直接数字频率合成器的硬件设计与实现

4.1 相位累加器

如6图所示，相位累加器是基于一个32位纹波进位加法器,与一串在相同的时钟相位上工作的全加法器。 全加法器的输出有内置寄存器与和位在内部反馈以执行累加。 用多路复用器(MUX)选择存储在寄存器中的32位频率控制字以执行累加，结果取高16位用于ROM表的寻址。

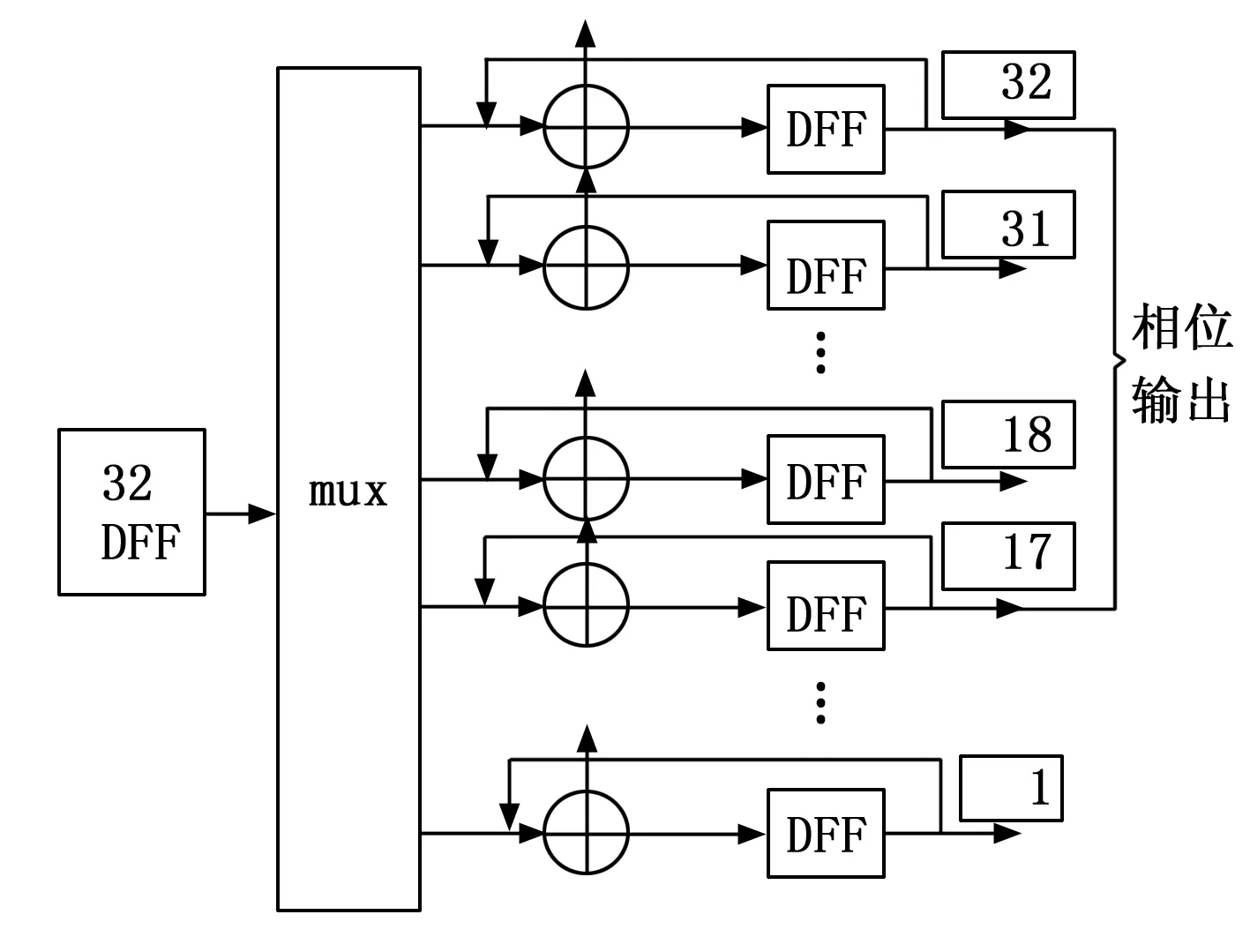
图6 相位累加器结构图

4.2 相位-幅度转换器设计

相位-幅度转换器设计的设计为本文的重点内容，包括四线近似算法和正弦相位差算法部分的数据重建以及QE-ROM算法的数据配置。结构如图7所示，地址位(α+β)以1:61的比例放大后重建出正弦相位差部分数据，四线近似算法中0<θ<π/8范围内的数据是通过向相位(α+β)下移1位生成的。π/8<θ<π/4部分的数据是通过将相位下移2位，并将相位的第一个和第二个MSB更改为10来生成。这些数据以1:61的比例放大后匹配量化和误差算法部分恢复后的数据。0<θ<π/4和π/4<θ<π/2的数据是对称的，因此，后半周期的数据由一个补偿器生成。

相位-幅值转换器结构如图7所示，总ROM由4个子ROM组成，即两个Q-ROM和两个E-ROM，用于分别存储coarse ROM和fine ROM中的数据。将四分之一相位累加器的输出分解为α+β+γ。coarse ROM和fine ROM的地址分别为α+β和α+γ。coarse ROM和fine ROM共享α地址位，因为α都是它们地址位中的最高位。因此，这四个子ROM共享一个行译码器以及四个不同的列复用器。图8显示了相位(α+β)、四次线近似算法幅度值以及重构1/2周期正弦波的四个ROM数据幅度值的相对位置，其中第一行表示9位的相位值，第二行表示11位的四线近似方法压缩后的数据幅度值，第三第四行分别表示coarse ROM中的量化值和误差值，第五第六行表示fine ROM中量化值和误差值，第七行表示加法器的输出。

图7 16位相位-幅值转换器

图8 数据位置表

4.3 电源模块设计

为做到设计目标中的需求，采用了全桥整流的方式完成交直流转换并利用全桥整流特性分离正负电压[11]；通过交流变压器及LM317和LM337两级降压、稳压实现±9 V及3.75 V降压输出；在电源模块的整体设计中均有为尽量减小电源噪声而进行的设计，通过整流桥后及降压输出端均使用滤波电容来降低电源纹波并且所采用的降压稳压芯片LM317和LM337噪声仅有38uvRMS。

本设计中采用了环形变压器来进行交流降压[16]，可较大幅度减小PCB面积及整体设计重量，并且内阻、磁干扰以及震动噪声较小，比较适合该设计中的高性能需求。设计中所用到的LM317和LM337为三端可调正电压低压差线性稳压器和三端可调负电压低压差线性稳压器，与同类器件相比，有较小的输入输出电压比，还有较为优越的电压和负载调节性能以及较小的输出电压误差，并且有较好的抗损性。采用输入跳线的方法，使输入既可以单端进行输入，亦可双端输入，提高了设计的可调节性；并且在稳压电路部分设计了以LM317、LM337与电位器组成的可调输出，使输出范围更加灵活；输出部分做到正负输出分别可控并且共用同一个公共地点，增加了输出的可控性同时也保证了稳定性；设计了LED指示灯，以便于工作状态的可视化。

图9 电源模块PCB图

4.4 DAC模块设计

在该模块的设计中，为减小整体体积及单片机管脚的使用，采用16通道串行DAC芯片AD5360来实现该设计；AD5360输出寄存器到输出端为透传模式，故通过LDAC引脚可控制DAC寄存器向输出寄存器传输的功能实现所有通道需同时同相位输出[14-16]；利用VREF引脚使AD5360的输出幅度控制在+7.5～-7.5 V，并通过缩小信号幅值至8.5 V、在输入信号中加入3.25 V直流分量的方式来调整输出范围+7.5～-1 V。

设计中所用的AD5360芯片其封装方式为LQFP-52，芯片内部集成两组16位的数模转换器，同时为了降低输出的误差在芯片封装的时候将每个数模转换器模块分开并且让其能够独立的调整设置增益以及失调，除此之外它的缓冲电压输出范围是基准电压的4倍。并且在PCB设计中采用了单点接地的方法分离数字地和模拟地，在二者之间添加一个0 Ω的电阻进行隔离，可以有效避免模拟地点的抖动带来的干扰；并且在各输入端添加电解电容来减小输入纹波，以此来减小输入噪声。

图10 DAC模块PCB图

5 系统仿真与测试

整体仿真是在vivado 2017.4开发环境下搭建工程，图11所示为对改进sunderland算法和量化误差算法压缩后的数据硬件实现全周期正弦函数的整体架构图控制模块的输入即为相位累加器输入端的频率控制字Fword、相位控制字Pword和幅度控制字Rword，输出为16位精度的正弦波幅度值[17-18]。顶层模块主要包含两个子模块，控制模块和接口模块。

图11 整体框架价结构图

控制模块主要完成控制4个存储单元中的量化和误差数据值按照其量化规则完成数据恢复，四线近似算法四条函数的阶段数据以及正弦相位差的数据还原。定义相位-幅值转换器中相位累加器的输出为Rom_Addr，因为Rom_Addr的最高两个有效位分别控制完成正弦数据由1/4周期向1/2以及全周期的重建过程，所以α+β+γ=14即a0+b0+c0=14。

assignc0=Rom_Addr[14]?～(Rom_Addr[4:0]):Rom_Addr[4:0];

assignb0=Rom_Addr[14]?～(Rom_Addr[8:5]):Rom_Addr[8:5];

assigna0= Rom_Addr[14]?～(Rom_Addr[13:9]):Rom_Addr[13:9];

X1、X2分别为coarse ROM和fineROM中对幅度进行量化后的相位。

图12 数据重建结构图

定义shift_1 <= {Rom_Addr[13:9],Rom_Addr[8:5]}>>1;

shift_2 <= {Rom_Addr[13:9],Rom_Addr[8:5]}>>2;

其中:shift_1、shift_2分别对应式(6)中0<θ<π/8以及π/8<θ<π/4范围内的数据。因为0<θ<π/4与π/4<θ<π/2部分的函数实对称的，所以后半周期的数据使用一个补偿器生成。

{Rom_Addr[13:9],Rom_Addr[8:5]}则对应正弦相位差算法作差时减掉的数据。三部分数据相加就会得到1/4周期的正弦波数据，1/4周期向1/2周期扩展以及1/2周期向全周期扩展则需要在Rom_Addr[14]以及Rom_Addr[15]的控制下通过两个补偿器来完成。

接口模块主要完成FPGA与数模转换器(DAC)数据传输所使用协议的时序设计以及DAC每个通道增益参数的设置[19-20]。AD5360芯片与外部硬件器件通讯的方式是采用4线串行的方式，其接口与DSP芯片的通讯接口完全兼容，同时还具有16个通道且每个通道最高可达到16位的输出精度，能够处理最高50 MHz的时钟速率。端口连接如图13所示。

图13 硬件接口图

其中:SYNC为片选信号，低位有效，选同时开始数据传输；SCLK为FPGA生成的门控时钟；SDI为串行输入信号；SDO为数据回读端口；RESET为复位信号，低位有效；LDAC为输出控制信号，可调节全通道同时通相位输出；CLR为数据清除信号，低电位有效，可清除通道的增益参数。BUSY为DAC数据处理进程信号。串并转换转换后的数据加上DAC通道地址位共计24位数据采用线性序列机由高到低依次输出。此次设计FPGA与DAC之间数据传输所用时钟为20 M，系统时钟设置为50 M，正弦波频率为200 Hz，DAC基准电压VREF设置为3.75 V。

图14为用vivado 2017.4对代码进行的仿真结果，器件选择为xc7z020clg400-2。FF触发器的使用量为144，占片上可以用总量的0.14%，LUT的使用量为176，占片上可使用总量的0.32%。片上总功耗为0.11 W。

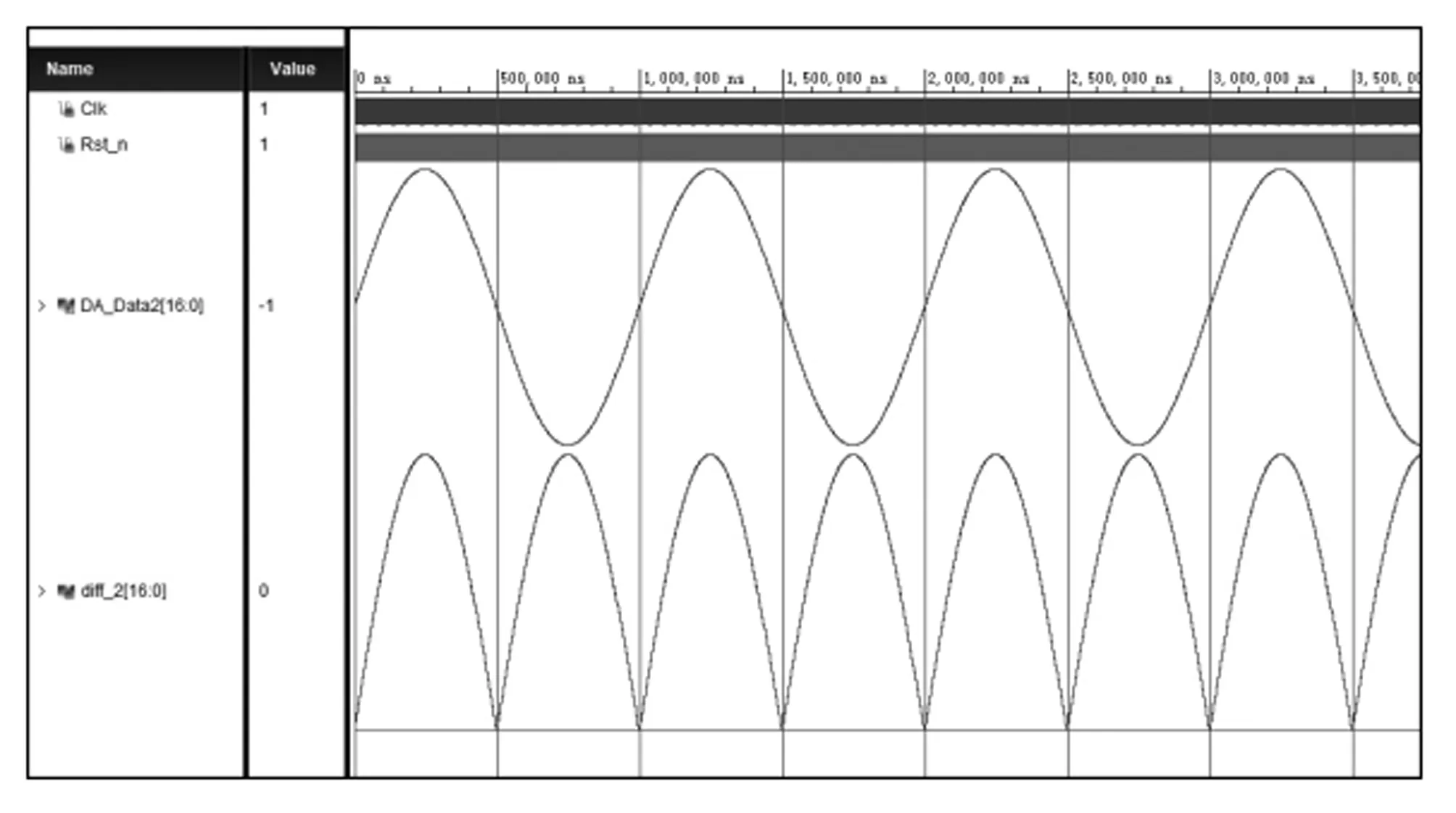
图14 Vivado 仿真结果图

以上正弦波形发生电路均vivado2017.3集成开发环境下搭建工程,利用Verilog硬件描述语言编写,并且编译通过。该 DDS信号发生器设计使用的BRAM位为两个仅占用 FPGA芯片可使用总量的1.43%。将编译生成的DDS.bit文件通过USB-Blaster下载FPGA 开发板上,并在数模转换器输出端连接示波器探头,测试结果如图15所示。

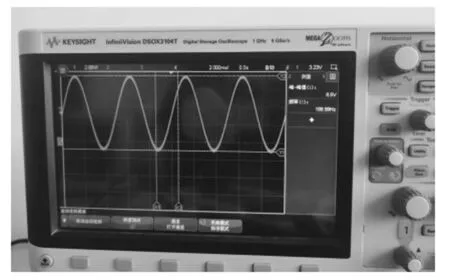
图15 正弦信号测试图

图15为DDS测试系统与正弦信号在示波器上的测试结果。图中显示正弦波频率为200 Hz，峰峰值为8.5 V，为满幅情况下DAC的输出电压，可以看到在不影响波形平滑度的情况下完成16位精度输出，并且ROM占用资源比传统方式节省99.2%。

6 结束语

本文提出了一种将改进sunderland算法与QE-ROM算法相结合的正弦数据压缩算法。改进sunderland算法是在sundeland算法的基础上利用正弦相位差算法与四线近似算法将coarse ROM中的数据作差后将差值部分存储到coarse ROM，这比原数据要小得多。QE-ROM再对整体数据量化，量化后的数据整体占用空间变小，对量化后的数据与量化误差分别保存。利用加法器对重建出[0,π/2]范围内的输出，然后结合正弦函数对称性通过补偿器重建出全周期的数据。本文提出的正弦数据压缩算法将正弦数据查找表(ROM)的尺寸从(216×16)压缩至(27×7+29×7+28×4+210×3) 8 576 bit，压缩比为122:1，尺寸仅为原来的0.8%.能够有效降低DDS芯片的面积和功耗。

但该算法也存在一定的不足之处,当频率控制字并非为2的整数次幂时，相位截断后锯齿波的周期不等于理想化连续时间锯齿波的周期，就会引入相位截断误差，相位截断误差序列的周期性是造成DDS输出频谱中含有大量杂散分量的主要原因之一。在算法的设计过程中，如果想要降低DAC的非线性误差以及ROM幅度量化的误差则可通过两方面来实现，一方面是采用更多位数的DAC器件，这样其精度可以随之得到提高，从而降低它的非线性误差；另一方面是增加ROM的字长从而实现降低它的幅度量化误差。同时要想在设计的过程中增加ROM地址位数的话，则在硬件的选型设计时就会更加的复杂。在设计的过程中需要考虑到的是DAC的非线性误差是与其位数成线性关系的，DAC的位数越大其对应的精度以及分辨率就会越高，则非线性误差也会越小；ROM幅度量化的误差是与ROM的字节长度成线性关系，与ROM的地址位数成指数关系，若ROM的字节长度越长对应的地址位数越多，则其幅度量化的误差也会越小。若在硬件方面增加对应成本便可以选择更多地址位数的ROM，但是在此情况下，其对应的相位截断误差在所有噪声的比率中会有所上升。因此如何提高对相位截断杂散的抑制来提高DDS性能需要进一步研究。