基于灰色系统理论的大学生就业去向预测

罗金焕，姚 珧，杨明秋，高全归

（1.玉溪师范学院 物理与电子工程学院，云南 玉溪 653100；2.玉溪师范学院 学生处，云南 玉溪 653100）

对毕业生就业去向有一个整体的了解是指导毕业生高质量就业的前提，对大学生就业率进行预测不仅可以帮助高校和教育部门了解大学生就业趋势，还能为就业指导老师提供指导方向以此促成毕业生高质量就业.

大学生就业率的预测有很多种方法，如专家系统预测[1,2]、多元回归分析预测[3]和灰色系统理论预测[4]方法.灰色系统理论主要研究“部分已知，部分未知”的对象[5]，非常适合就业预测.本文将2014-2022 年云南省某地方高校毕业生的就业去向划分为“已就业”“升学和入伍”“编制内就业”和“编外就业”4 类，运用灰色系统理论中的GM（1,1）模型预测该校2023 年的就业情况.并探讨出一种误差修正的方法，给出预测误差.

1 GM（1，1）预测模型及模型的修正

1.1 GM（1，1）预测模型

如果有一个有序的序列可写为[6]

该序列中的每一项都是非负项，则可以对该序列进行运算，运算后得到

通过上述运算可以得到新的序列，即一次累加序列为

方程（3）中的序列S(1)(k) 呈现出的变化趋势可以近似的用微分方程表示出来.可将该微分方程写为[6]

方程中的a，b为模型参数，这两个参数可以由以下计算得出.[4]取

其中，

利用（6）式和方程（1）（3），就可计算出参数a和b.利用参数a和b就可以求解微分方程（4）.方程（4）离散形式的解可写为[6]

考虑初始条件S(1)(0)=S(0)(1)，上式可改写为[6，7]

1.2 模型的修正

考虑到对序列预测时，本方法认为前t0-1 个数据点是已知的，从第t0个数据点才需要进行预测.根据误差构建新的误差序列

采用类似方程（2）的运算，得到新的序列

建立与方程（4）相似的微分方程，对其求解，得到误差方程的解，表示为

将该方程的解转化到原始误差序列，可得误差修正项可表示为：

综合方程（8）和（13）可得到较为精确的修正预测结果.

2 模型在大学生就业预测中的应用

2.1 整体就业率预测

统计2014-2022 年云南省某地方高校毕业生就业数据，为了准确区分就业类型，本研究中统计的就业人数不包含自由职业者，本文将类别为：出国工作、地方基层就业、国家基层就业、科研助理、其他录用形式、签就业协议形式就业、签劳动合同形式就业、签约、研究生、应征义务兵、自主创业、地方特岗教师、国家特岗教师、西部计划、三支一扶、第二学士学位、参加公招考试录用、选调生、专升本人数加总后界定为就业总人数；将类别为：研究生、第二学士学位、应征义务兵、专升本人数加总后界定为升学和入伍总人数；将类别为：地方基层就业、国家基层就业、地方特岗教师、国家特岗教师、西部计划、三支一扶、参加公招考试录用、选调生人数加总后界定为编制内就业总人数；将类别为：出国工作、科研助理、其他录用形式、签就业协议形式就业、签劳动合同形式就业、签约、自主创业人数加总后界定为编制外就业总人数.利用已有数据，可计算出2014-2022 年的就业率（就业人数与毕业人数的比值），各年就业率见表1.

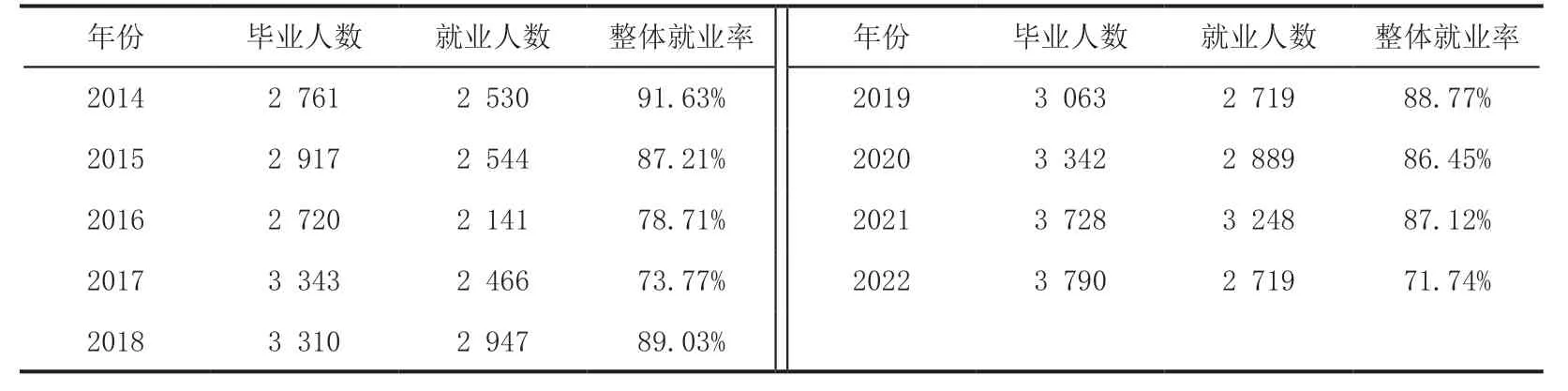
表1 2014-2022 年云南省某地方高校整体就业率

表1 中给出了云南省某地方高校2014-2022 年的整体就业率，为了进行模型预测误差的修正，在实际计算中，首先以2014-2016 年（3 年）的就业率为已知序列预测，模型预测出的2017 年就业率为70.99%，该校2017 年的实际就业率为73.77%.模型预测结果与当年的实际就业率的差就是模型预测的误差，由此可得到2017 年的模型预测误差.以此类推，可得到2017-2022 年的模型预测误差序列.以此序列为基础，根据本文1.2 节的方法可计算2023 年的模型预测误差.

本文模型的预测结果见图1.图中，黑色数据点为实际就业率，浅黑色数据点为模型预测结果，图中给出了2023 年就业率的预测误差.

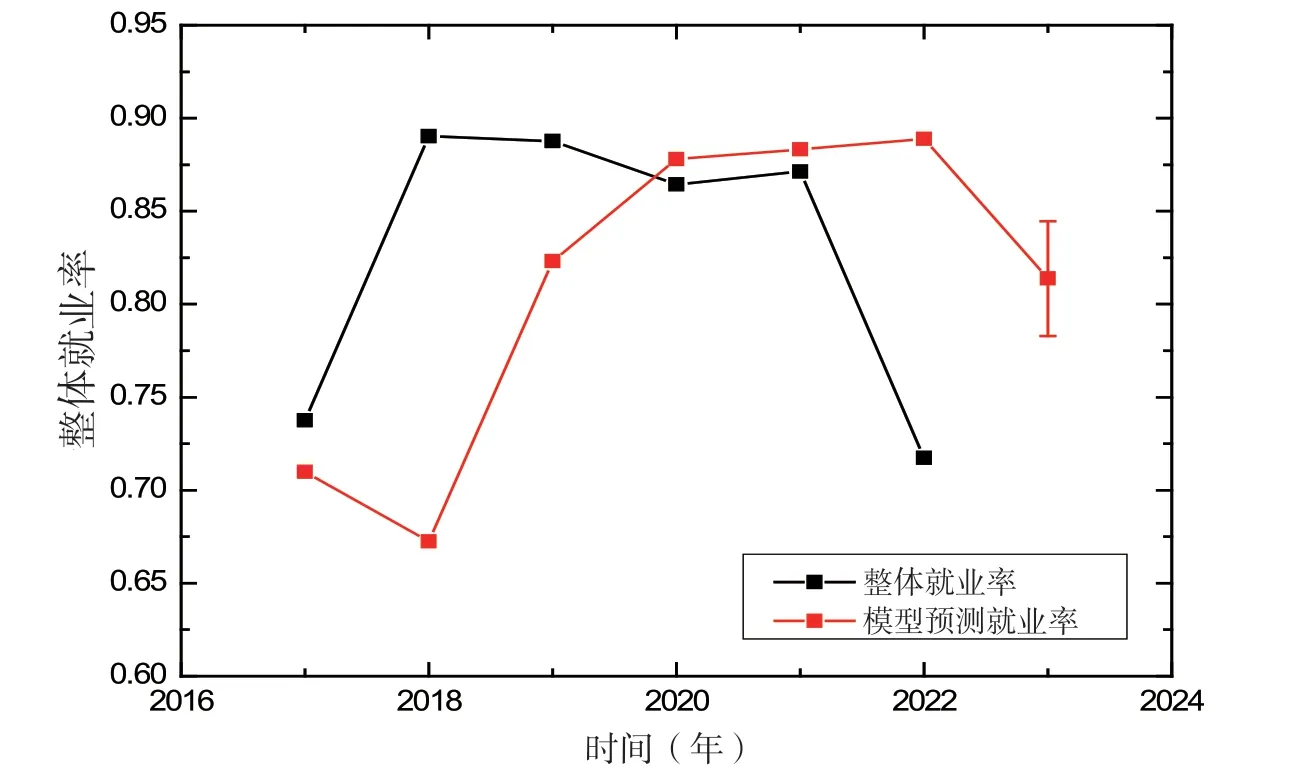
图1 云南省某地方高校2023 年整体就业率预测

在此需特别说明2018 年的就业率比2017 年大幅度上升，模型预测数据与真实数据存在较大偏差，其原因是2018 年人力资源社会保障部印发了一些就业政策，其中在《关于做好2018 年全国高校毕业生就业创业工作的通知》中指出要把高校就业放在首要位置，鼓励毕业生到基层和艰苦地方工作，鼓励中小企业和民营企业聘用高校毕业生等，这些政策扩大了市场人才需求，使2018 年大学生就业率大幅度上升.图1 中的实际就业率体现了政策在实际就业中的指导作用，而模型预测无法体现就业政策的影响，这导致2018 年的就业率的预测误差较大，2019-2021 年的预测误差明显减小.同时也表明模型预测具有时间积累效应，而就业政策能起到立竿见影的效果.模型预测结果表明，2023 年云南省某地方高校的毕业生就业率预计为（81.4±3.1）%.

2.2 就业去向的预测

表2 统计了2014-2022 年云南省某地方高校毕业生升学和入伍的比例.采用与整体就业率预测的相同方法，可以预测2023 年入伍和升学人数所占的比例.预测结果由图2 给出，图中黑色数据点表示2014-2022 云南省某地方高校毕业生实际的升学和入伍比例，浅黑色数据点表示的是模型的预测结果.模型的预测结果表明，云南省该高校2023 年入伍和升学人数占毕业生的比例预计为（9.95±0.80）%.同时，由图可见，模型预测结果逐渐趋于稳定，这一结果也表明，将升学和入伍作为一个整体进行预测是合理的.

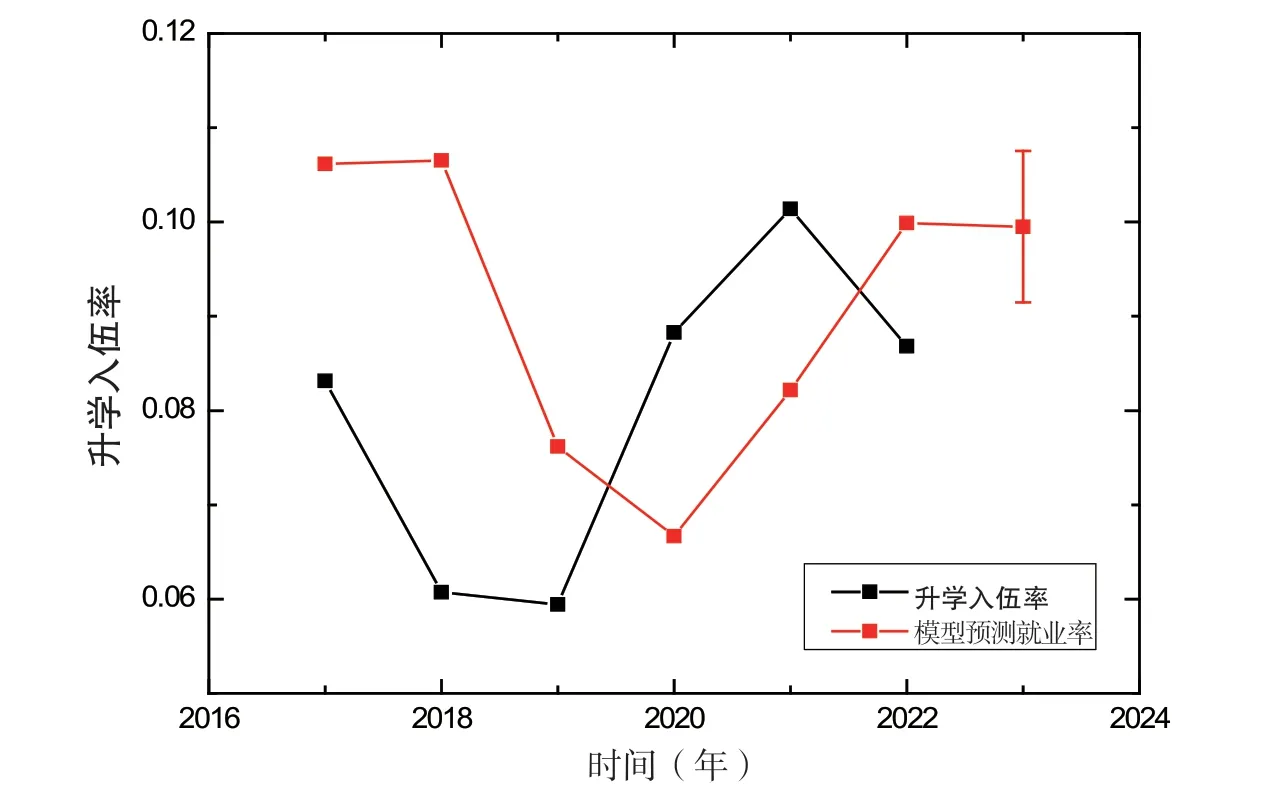
图2 升学入伍就业率预测

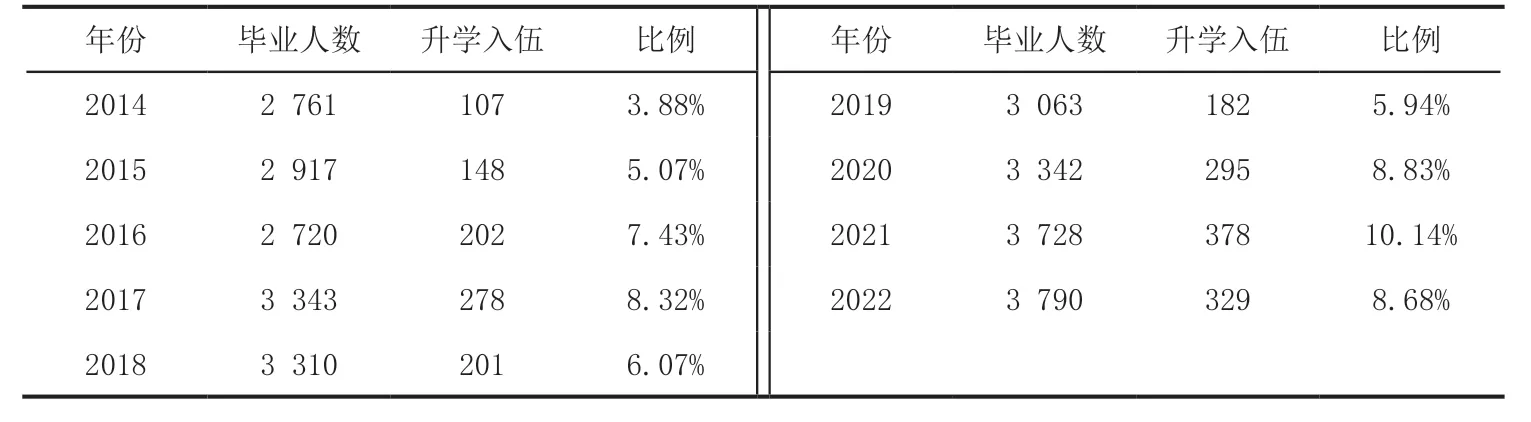
表2 升学和入伍占毕业生比例

表3 统计了2014-2022 年云南省某地方高校毕业生编制内的就业率.利用模型可分别预测2023 年的编制就业率和预测误差.

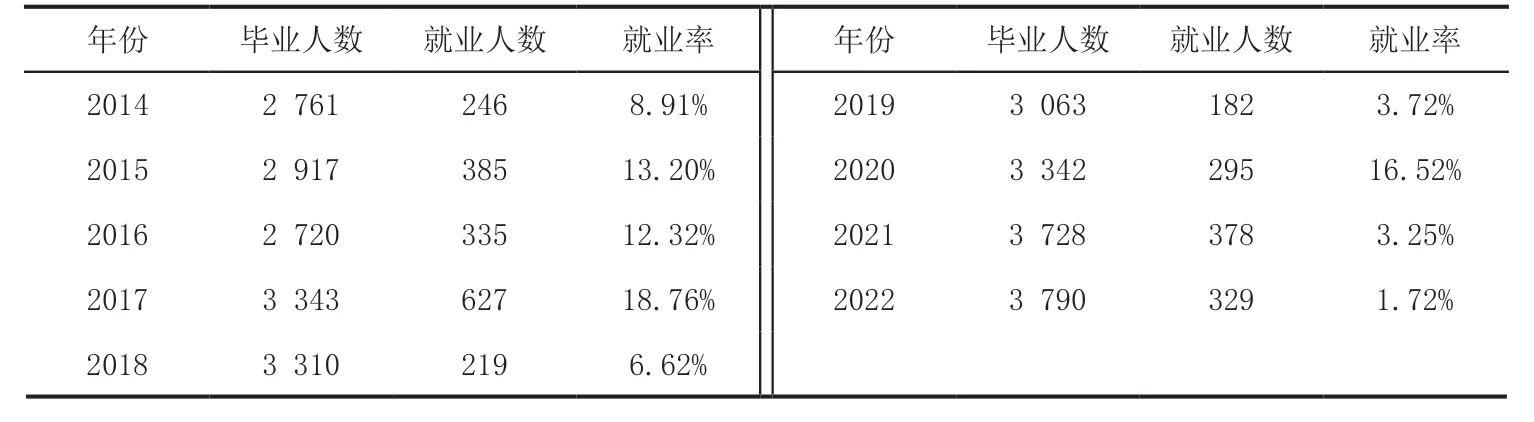
表3 编制内就业率

预测结果由图3 给出，图中黑色数据点表示2014-2022 云南省某地方高校毕业生编制内就业率，浅黑色数据点表示的是模型的预测结果.模型的预测结果表明，该校2023 年毕业生编制内的就业率预计为（4.6±3.7）%.这一预测结果的误差较大，其主要原因是2020 年时，由于疫情带来的就业压力，云南省组织了规模较大的“613”事业单位专项招聘，使得2020 年的编制内就业率明显增加.模型预测中无法考虑这一因素，因而，预测误差较大.这一结果与实际情况相符，预测结果是合理的.

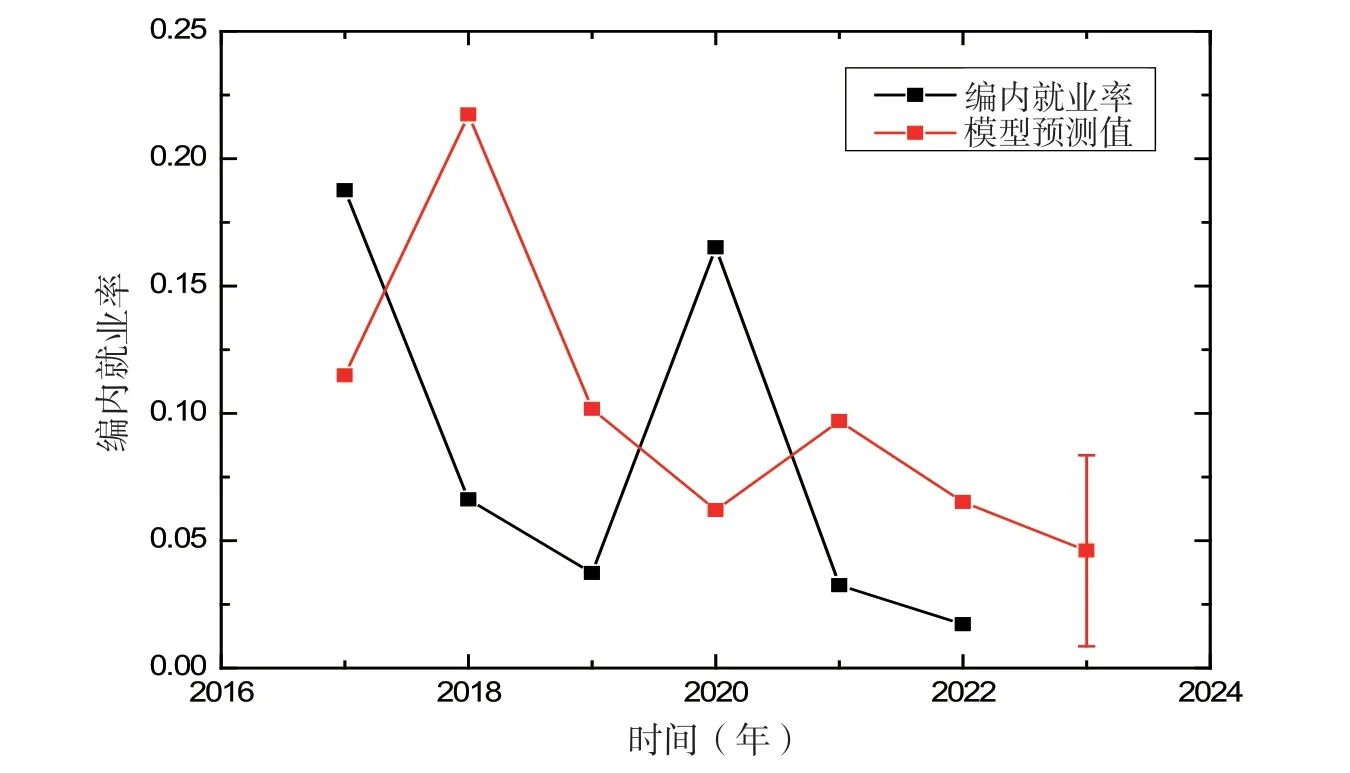
图3 毕业生编内就业率预测

表4 统计了2014-2022 年云南省某地方高校毕业生的编外就业率.利用模型可分别预测2023 年的编外就业率和预测误差.图4 中黑色数据点表示2014-2022 云南省某地方高校毕业生编外就业率，浅黑色数据点表示的是模型的预测结果.由图4 看，该高校2023 年编外就业率预计为（69.3±3.6）%.

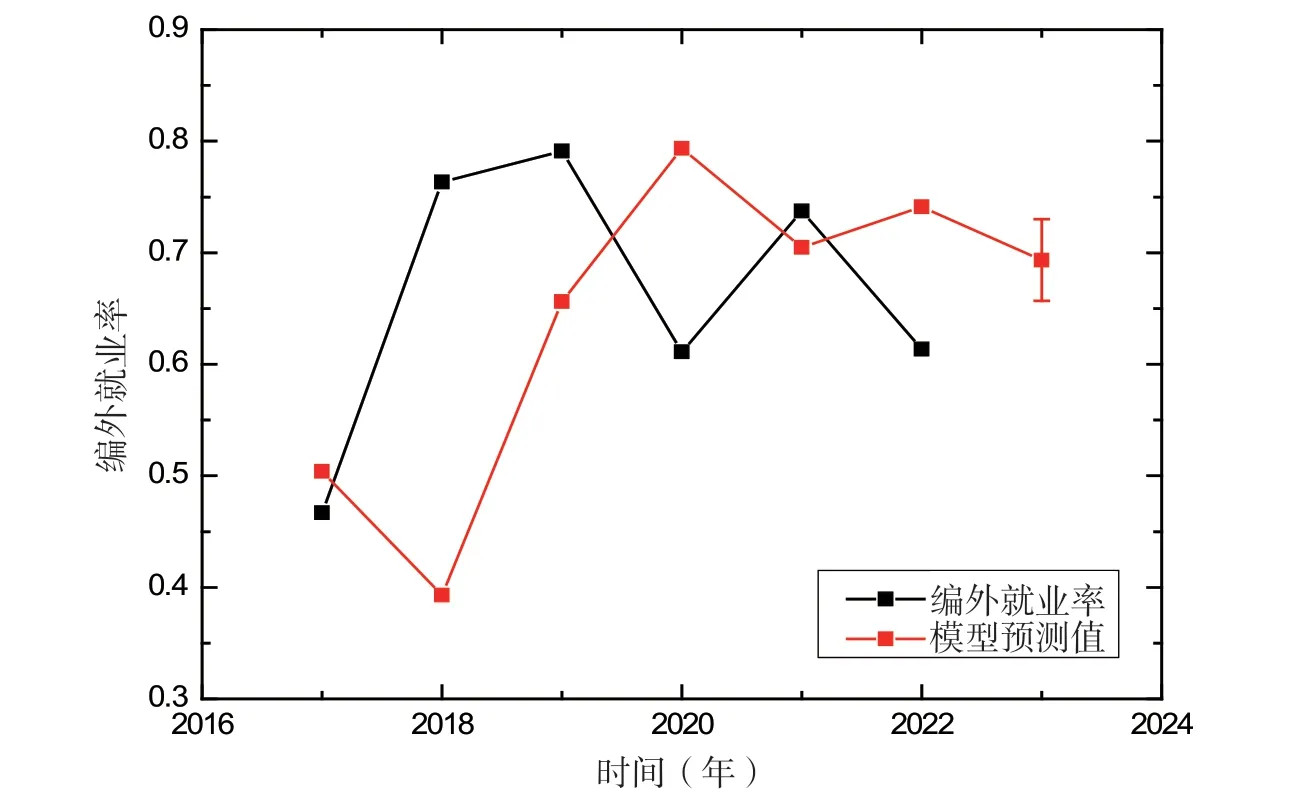
图4 编外就业率预测

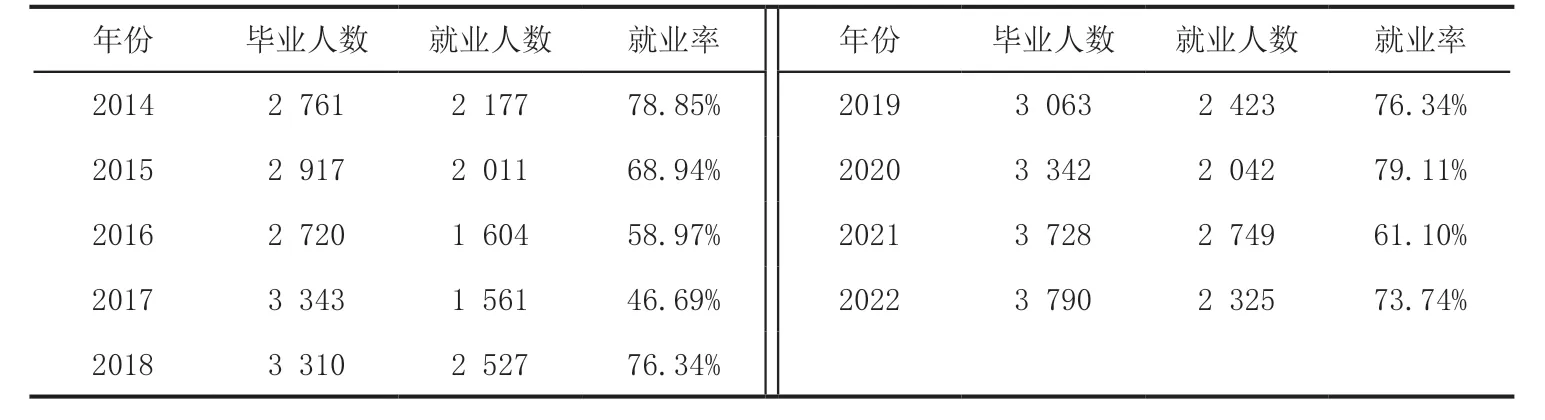
表4 编外就业率

3 结 论

本文基于灰色系统模型GM（1，1）开展了云南省某地方高校毕业生就业去向的预测，考虑到灰色系统模型预测的不准确性，本文提出了一种基于灰色系统预测误差修正的方法.利用灰色系统模型，并考虑误差修正，计算结果表明，云南省某地方高校2023 年整体就业率预计为（81.4±3.1）%，其中升学和入伍的人数占比预计为（9.95±0.80）%，编制内就业率预计为（4.6±3.7）%，编外就业率预计为（69.3±3.6）%.

灰色系统模型完全根据过去几年的就业数据预测未来的就业情况，无法考虑就业政策，社会环境等方面对就业的影响.因而，灰色系统模型的预测会存在误差，但本文考虑了预测误差的修正，能够提高预测精度.