非凸低秩张量补全的随机算法

南佳琨,王川龙*

(太原师范学院 数学与统计学院 山西省智能优化计算与区块链技术重点实验室,山西 晋中 030619)

0 引言

张量是向量和矩阵的高阶推广,随着信息的飞速发展,关于张量及其应用的研究受到越来越多的关注,张量补全更是成为许多学者的研究热点之一.张量补全可以应用到图像恢复[1,2]、数据挖掘[3]、机器学习[4]及信号处理[5]等领域.张量补全是指从存在缺失、污染的数据中恢复原始数据,其数学模型为:

(1)

与矩阵的秩不同,张量的秩是更复杂的.在现有的工作中,张量的秩可以表示为多种形式,如CP秩[6],Tucker秩[7],张量火车(TT)秩[8],张量环(TR)秩[9]等等.本文主要讨论Tucker秩模型.当Tucker秩是已知的情况下,张量由HOSVD生成的核心张量和因子矩阵组成[10].当模型(1)的秩为Tucker秩时,可以写成如下形式:

(2)

(3)

并提出三种有效算法来求解此凸模型.Gandy等[12]用张量的秩作为稀疏表示,提出张量恢复问题的Douglas-Rachford算法.Ng等[13]通过考虑不同展开矩阵所起的作用不同赋予不同的权重,给出了自适应加权张量核范数模型,该模型对张量按模展开的矩阵进行了有效地平衡,从而获得更好的补全结果.王川龙等[14]基于模型(3)利用随机思想设计高效的交替方向法,进一步减少计算复杂度提高算法效率.低秩张量补全的凸松弛模型能收敛到全局最优解并且有很好的理论保证.但是在很多情况下,凸松弛模型的解并不能很好地近似原问题的解.为此,非凸逼近模型受到了关注.Li等[15]给出一种用张量每个模展开的p-范数近似Tucker秩的非凸Schatten-p范数模型,并采用交替方向乘子法求解此问题.Ji等[16]提出了一种基于对张量的每种模式展开进行对数加权求和的非凸对数函数模型来逼近低Tucker秩张量模型,其对数函数(Log-Det)模型为:

(4)

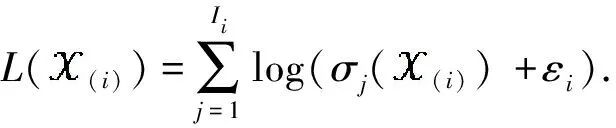
1 符号和预备知识

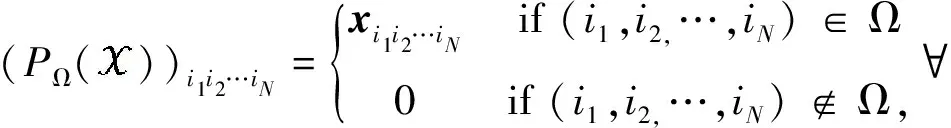
定义1(奇异值分解(SVD)[17]) 对于秩为r的矩阵X∈I1×I2,则必存在正交矩阵U∈I1×r和V∈I2×r,满足

X=UΣrVT,Σr=diag(σ1,σ2,…,σr),

其中σ1≥σ2≥…≥σr≥0.

定义2(矩阵核范数的次微分[18]) 对于秩为r的矩阵A∈I1×I2,存在奇异值分解A=UΣrVT,则的次微分为:

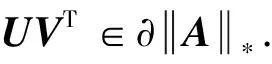
Dτ=UDτ(Σ)VT,Dτ(Σ)=diag({σi-τ}+),

2 算法

通过引入辅助变量,模型(4)可以等价为如下模型:

(5)

文献[16]基于模型(4),并结合交替方向乘子法(ADMM)框架,给出如下算法求解非凸对数函数模型.该算法具有较好的补全效果,其算法如下:

算法1基于Log-Det的低秩张量补全(LRTC-Log)算法.

第2步:计算

fori=1∶Ndo

end for

由算法1可以看出,在每次迭代过程中,都需要计算N次奇异值分解,此时花费时间较大,引入随机思想,使得每次迭代过程中,随机选取一个张量模展开面进行奇异值分解,大大减少了计算时间.其算法如下:

算法2基于Log-Det的随机ADMM算法(SADMM)

第1步:令Rk+1=randperm(N,1),

3 收敛性分析

假设A

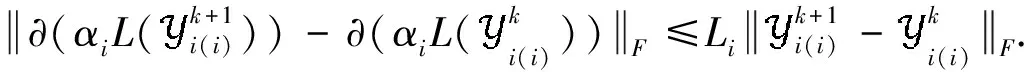
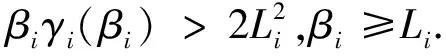
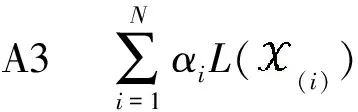
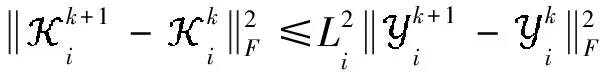
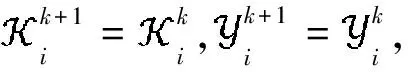
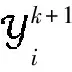
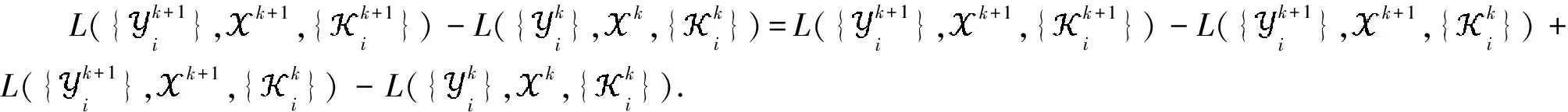
其中第一项为

(6)

第二项可以被表示为

(7)

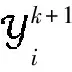
证明

(8)

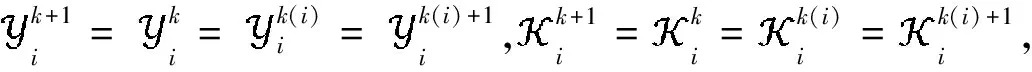
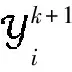
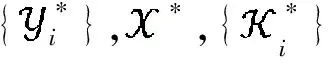
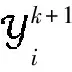
(9)

在算法2中,对

(10)

4 数值实验

将算法2与算法1,HaLRTC算法在随机张量补全,图像修复的数值试验中进行比较,从而证明算法2的有效性.所有数值代码均在Matlab(R2019b)软件编写,运行环境为戴尔(DELL)PowerEdge R740xd高性能2U机架式并行运算服务器.

4.1 随机张量补全

在随机生成的数据上比较所提出的算法,随机张量通过张量的Tucker分解生成:

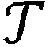
表1 当p=0.3时,算法SADMM、LRTC-Log、HaLRTC的比较

表2 当p=0.2时,算法SADMM、LRTC-Log、HaLRTC的比较

表3 当p=0.1时,算法SADMM、LRTC-Log、HaLRTC的比较

实验结果表明,新算法比LRTC-Log算法和HaLRTC算法所需的CPU时间更少且精度好.

4.2 图像填充

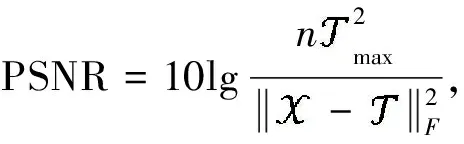
图1 (a)(f)(k)为原始彩色图像,(b)(g)(l)分别为采样0.3,0.2,0.1的图像,(c)(h)(m)为SADMM算法的补全图像,(d)(i)(n)为LRTC-Log算法的补全图像,(e)(j)(o)为HaLRTC算法的补全图像

表4 “lena”图像在不同采样率下,三个算法的比较

针对彩色图片填充的实际问题,表4可以看出,在时间花费上,新算法明显少于其他两种算法,修复效果较好.

5 总结

基于非凸对数函数的张量补全,引入一种随机算法.该算法在迭代过程中,不需要对每一步的所有变量进行更新,只随机选取一个子问题进行优化,大大减少了计算量,提高了计算效率.随后在一定假设条件下,证明了算法的收敛性.最后,通过随机张量补全数值实验可以看出,新算法比其他算法的花费时间少且精确度好,对比彩色图像修复实验,新算法同样在时间上占据一定的优势.