基于点云空间分布特征的多级索引结构
2023-03-02杨丽娟崔钰琳杨紫骞翟光杰
杨丽娟,崔钰琳,杨紫骞,翟光杰,王 超
(1.中国科学院国家空间科学中心,北京 100190;2.中国科学院大学,北京 100049)
1 引 言
点云数据是三维空间中离散分布的一组点,广泛应用于地形测量、文物保护、三维重建、城市规划、智能驾驶、虚拟现实等领域[1-4]。点云空间分布离散无序,数据量巨大,为后续的数据处理带来了挑战。建立合理高效的空间索引机制,是实现数据高效检索和快速调度的关键,是后续数据处理的前提[5]。传统的单一索引模型难以对海量点云数据进行高效组织管理,混合索引模型通常结合了两种及以上不同索引的优势,是当前研究的重点[6]。
文献[7]提出了一种八叉树和三维R树集成的空间索引方法,显著提升了空间利用率和空间查询效率。文献[8]提出了一种多级格网和KD树相结合的混合空间索引,既提升了查询效率,又解决了单一分辨率数据冗余的问题。文献[9]将点云的方向信息引入传统的模糊c-均值,并使用BSP树对点云进行逐点划分,使索引能够沿着点云的空间结构扩展,避免产生不必要的分区。文献[10]提出了一种全局KD树和局部八叉树相结合的两级混合索引结构,实现了树结构的均衡,并能以块为单位对海量点云进行快速检索。文献[11]提出了一种结合KD树空间切分思想的类八叉树索引结构,降低了内存空间占用和邻域搜索耗时。文献[12]将快速划分空间的八叉树和高效查询空间的三维R*树相结合,构建了一种名为3DOR*-tree的混合空间索引结构,实现了三维地质四面体模型的有效访问和高效查询。文献[13]针对地铁隧道的点云数据特点,提出了一种格网和多分辨率八叉树结合的索引模型,提升了空间分布不平衡但集中的线状点云的索引构建效率和质量。
这些方法的空间划分都是基于空间规律性和轴对齐包围盒的,无法表达点云本身的空间结构。因此,针对点云分布的不规则性和非均匀性,将方向包围盒引入传统的规则八叉树结构,提出了一种方向八叉树空间划分方法。在全局索引中,采用方向八叉树组织点云数据。通过对点云结构进行主成分分析,自适应地计算包含一组点的每个节点的方向包围盒。为提升索引模型的检索能力,在局部索引中,增加KD树来管理方向八叉树的叶子节点。
2 方向八叉树索引结构
2.1 八叉树结构
八叉树结构通过对大小为2n×2n×2n的三维空间实体进行循环递归的体元剖分,其中每个体元的时间和空间复杂度相同,从而构成一个方向图[14]。如果被剖分的体元属性相同,则构成一个八叉树的叶节点;否则将该体元划分为8个子立方体,并依次递归划分。八叉树划分及结构示意图如图1所示。

图1 八叉树结构示意图
传统的八叉树首先为点云数据建立轴向包围盒,之后递归地将空间规则地划分成八个均匀的子立方体,并将空间中的数据分配到相应的子立方体中,可以实现对海量点云数据的高效管理。但是,易产生大量的空白节点,影响树的平衡性[15]。
2.2 方向包围盒
方向包围盒是沿着物体的主成分方向生成的最小立方体包围盒。因此,相较于轴向包围盒,方向包围盒可以根据物体的形状特征尽可能紧密地逼近物体,紧密性更好,能显著降低冗余空间。计算方向包围盒主要是借助顶点坐标的一阶及二阶统计特性来确定最佳方向,并寻找包围盒在该方向上的最小尺寸[16]。
本文采用了一种利用三角网计算方向包围盒的方法[17],具体步骤如下:
Step1:三角面片的平均向量如式(1)所示:
(1)
其中,n代表三角面片的总数;pi、qi和ri分别表示的是第i个三角面片的三个顶点的坐标向量。
Step2:协方差矩阵C计算如下:
(2)
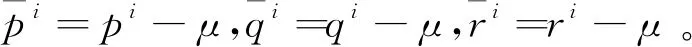
Step3:计算协方差矩阵C的特征向量,确定方向包围盒的方向和尺寸。对特征向量进行单位化,将其作为一个基。由于矩阵C是对称矩阵,因此特征向量基是正交的。沿基的每个轴向找到该轴向上的极值顶点,并由极值顶点确定方向包围盒的尺寸[18]。将轴向作为方向包围盒的方向。
2.3 方向八叉树的思想与构建
方向八叉树是一种用来描述三维空间的树状结构模型。方向八叉树的每个非叶子节点代表对应空间数据的方向包围盒。每个节点空间可以均匀分割成8个子立方体,8个子立方体对应的点集组成当前节点的8个子节点。如果子节点满足分割条件,则对其进行递归划分,直至满足分割停止条件。
方向八叉树的输入是原始点云集P,组织构建步骤为:
Step1:初始化分割阈值Toc。本次实验中,Toc设为原始点集数量的0.2 %。
Step2:使用原始点云集P作为树的根节点。
Step3:如果当前节点中的点云数量大于Toc,计算节点的方向包围盒。
Step4:根据包围盒将空间分解成8个子立方体,并将每个子立方体对应的点集作为当前节点的8个子节点:
由包围盒的中心位置,转换节点中的点集坐标:
(3)
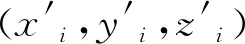
根据转换后的坐标点在每一轴上的正负性,将原始点分配到对应的子节点中。
Step5:如果子节点所存储的点云数量与父节点一样且不为零,则停止当前节点的细分。
Step6:迭代执行步骤(3)至(5),直到节点中的点云数量均小于或等于Toc。
2.4 八叉树与方向八叉树的比较
由于三维点集的划分较为复杂,为了清晰明了地展示思路,如图2所示,分别使用四叉树和方向四叉树对二维点集的空间划分来示意比较。树的分割阈值设置为3。图2(a)、图2(b)分别表示四叉树的空间划分和划分后形成的树结构,图2(c)、图2(d)分别表示方向四叉树的空间划分和划分后形成的树结构。非空节点率定义为所有节点中非空节点的占比。四叉树产生了25个节点(18个叶节点,3个空节点),非空节点率是88 %;方向四叉树产生了 21个节点(16个叶节点,1个空节点),非空节点率是95 %。

图2 二维点集的空间划分比较
可以看出,与四叉树相比,方向四叉树在节点总数、叶节点数、空节点数和非空节点率上都有更好的结果,有助于减少节点数量和冗余节点。
3 多级索引结构
3.1 KD树结构
KD树是一种对多维欧氏空间进行划分而构造的二叉树。每个非叶节点代表一次空间划分。每次划分时,选择其中某一维度进行比较,并使用一个合适的数据点作为划分标准,将当前空间划分成两个子空间[19]。可将垂直于划分维度且经过划分数据点的平面视作一个超平面。节点的左子树代表超平面左边的点,右子树代表超平面右边的点。
为了使KD树具有更好的平衡性,每次划分应尽量使数据点集均匀分割成两部分。通常,与其他维度相比,数据点集在划分维度上应分布尽量分散[20]。因此,可选择所有数据点方差最大的维度作为划分维度,并取划分维度上的中位数对应的点作为划分数据点。以划分数据点在划分维度上的值为标准,将其余数据点分配到左、右子树上。如果当前数据点在划分维度上对应的值小于标准值,则将其划分到当前节点的左子树,反之,则划分到当前节点的右子树。如图3所示,KD树将二维及三维空间分割成多个子空间。
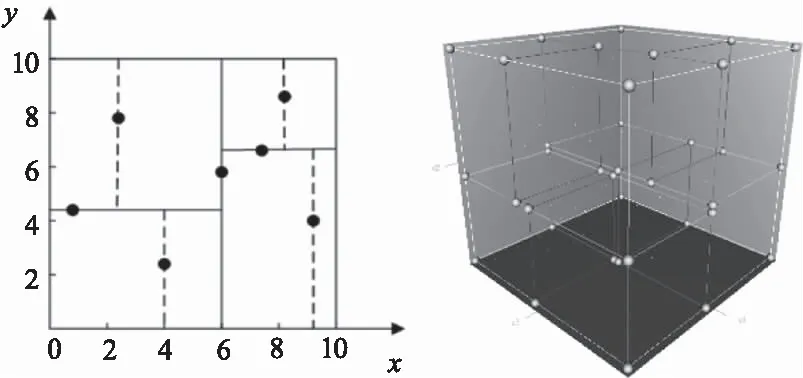
图3 KD树分割
3.2 多级索引结构的思想
KD树能实现点云的快速查找,但由于建树期间占用内存过大,难以对海量点云进行构建。而方向八叉树构建简单、快速,查询效率受限于分割阈值。因此,可结合二者优势,基于方向八叉树和KD树建立混合索引结构。在上层采用方向八叉树对点云进行全局划分,在下层使用KD树对局部点云信息进行组织,递归划分方向八叉树叶节点,直至KD树叶节点内的点数不超过提前设置的阈值。划分后的空间信息存储在方向八叉树叶节点中,如图4所示,形成全局方向八叉树和局部KD树的多层混合索引结构。

图4 多级索引结构
3.3 多级索引结构的构建
建立基于三维点云空间分布特征的多级索引结构的具体步骤如下:
Step1:使用初始点云P构建一个方向八叉树。
Step2:为每一个叶子节点Qi构建KD树,具体操作如下:
①叶子节点的点集作为KD树的根节点。
②如果当前节点中的点数大于Tkd,当前节点继续细分。其中,Tkd=N/2m,N表示点云数据集的大小,m表示KD树递归分解层数。
③根据点集空间的轴向包围盒,计算点集在各个维度上的方差:
(4)
(5)
(6)

选择具有最大方差的维度,来确定分割维度:
sd=max(sx,sy,sz)
(7)
以空间中分割维度上的中值点作为分割点,根据分割维度,将空间划分成两个子空间,子空间中的点集作为当前节点的子节点。
④迭代执行②至③,直至节点中的点数均小于或等于Tkd。叶子节点中的点集以及每个节点点集的包围盒,即为划分结果。
索引构建的流程如图5所示。
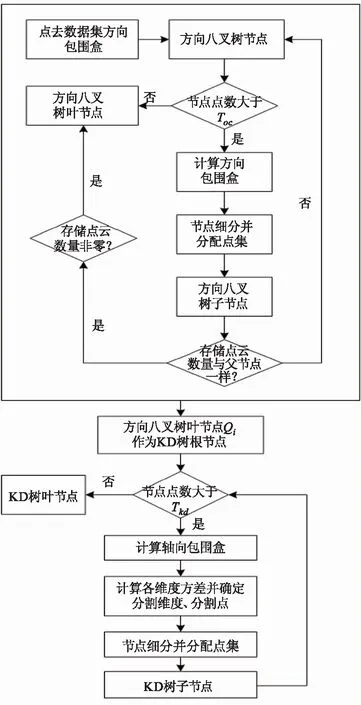
图5 多级索引构建流程
4 实验结果与分析
为验证所提方向八叉树在节点冗余方面的提升,本文使用经典八叉树与方向八叉树进行对比实验。同时,为验证本文基于三维点云空间分布特征的多级索引的结构有效性,将KD树、八叉树、四叉树—KD树与基于三维点云空间分布特征的多级索引进行比较。比较指标包括构建索引消耗时间、邻域搜索时间。最后,通过实验探索方向八叉树分割阈值对多级索引结构构建时间以及构建内存的影响。
4.1 实验数据与环境
根据空间分布特征和数据量,本文选择了三种类型的点云数据进行实验。第一类数据是The Stanford 3D Scanning Repository中的典型点云数据;第二类数据是RGB-D Object Dataset中的常见室内环境点云数据;第三类数据是大型自然场景的海量三维点云数据。数据点的数量级分布是103~108。实验环境是Intel(R)Core(TM)i5-7200U CPU @2.50 GHz,12 GB内存。
4.2 方向八叉树与八叉树节点实验
表1显示了八叉树与方向八叉树的节点对比,对比项包括节点总数、空节点数和非空节点率。在所有数量级的点云数据上,与八叉树相比,方向八叉树生成的总节点数和空节点数均更少。同时,方向八叉树结构的非空节点率有较为显著的提升。八叉树的非空节点率集中分布在83 %~90 %,而方向八叉树的非空节点率集中在88 %~96 %范围内,空间利用率提高了5 %。

表1 各方法针对不同点云数据的节点比较
4.3 索引构建时间实验
四种索引的构建时间对比如表2所示。其中,KD树建树耗时最长,远大于其他三种方法,且随着点云数量级的增加,差异逐渐扩大。当点云数量达到100万时,KD树建树耗时比其他方法多65~91 s。当点云数量超过1000万时,KD树会由于内存不足而无法完成建树。四种方法中,八叉树索引构建速度最快。由于引入了方向信息,基于三维点云空间分布特征的多级索引建树时间增加,但明显快于四叉树—KD树混合索引,与八叉树相差不大。
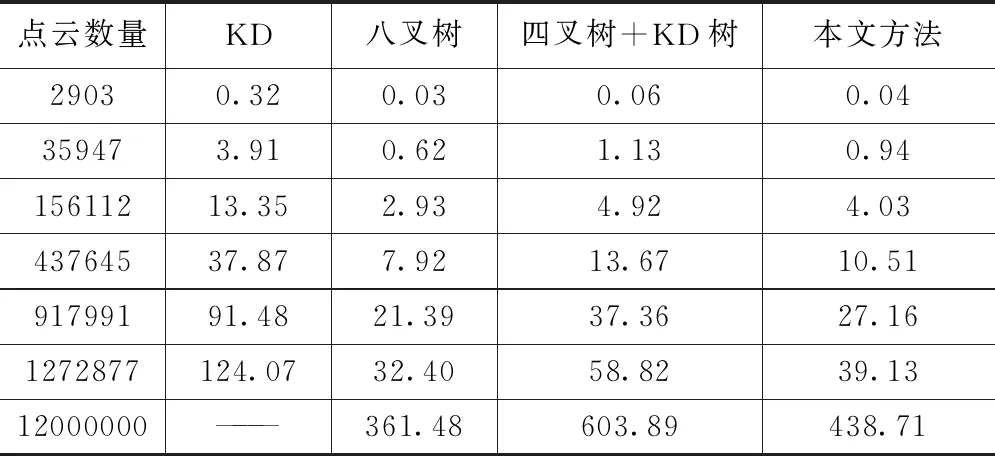
表2 各方法索引构建时间对比(单位:s)
4.4 邻域搜索耗时实验
邻域搜索耗时是指搜索指定的每一个点的最邻近点所消耗的平均时间。本文方法与其他三种方法相应指标对比如表3所示。通过对比可知,八叉树搜索耗时最长,查询效率远低于KD树。与单一索引结构的查询效率相比,混合结构的索引方式的查询效率有着明显优势。本文方法和四叉树—KD树结构查询效率均在KD树基础上有所提升,相比于八叉树结构提升了1~2个数量级。与四叉树—KD树混合索引结构相比,本文方法邻域搜索速度更快,具有更好的查询性能。

表3 各方法邻域搜索时间对比(单位:ms)
4.5 方向八叉树分割阈值实验
不同数量级的点云数据构建混合索引所消耗的时间、空间与方向八叉树分割阈值的关系如图6、图7所示。索引构建时间及内存占用主要与点云数据量相关,不同方向八叉树分割阈值对同一点云的构建影响较小。同时,点云数据量越大,方向八叉树分割阈值产生的影响越大。对于数据量较大的点云,当上层方向八叉树分割阈值逐渐增大时,构建索引所消耗的时间和空间先有明显的下降,之后下降幅度逐渐减弱,最后趋于平缓。因此,对海量点云的索引构建而言,选择合适的方向八叉树分割阈值能节省大量时间及空间占用,具有重要意义。

图6 不同方向八叉树阈值下构建索引时间

图7 不同方向八叉树阈值下构建索引占用内存
5 总 结
本文针对海量不规则点云管理困难,时空消耗大的问题,根据点云分布特征,将空间分布特征引入八叉树,提出了一种新的空间划分方法——方向八叉树,来适应点云数据的非均匀空间分布。在此基础上分析了方向八叉树和KD树的优缺点,并设计了方向八叉树与KD树结合的双层点云管理模型,进一步提高索引查询效率,对点云数据进行合理管理。实验表明,方向八叉树结构相比于传统八叉树,空间利用率提高了5 %左右。且本文提出的基于空间分布特征的多级索引结构,构建索引耗时接近于八叉树,相比于KD树、四叉树—KD树混合索引提高了25 %;与其他三种索引结构相比,邻域搜索效率提高了18 %,充分验证了本文方法的有效性。
但本文提出的索引方法仍有很多可改进之处。例如,对海量点云数据而言,上层方向八叉树分割阈值对索引构建时间、空间有较大影响,但目前难以通过简单、自动的方法确定最优的分割阈值;方向八叉树与八叉树的树结构高度相差不大,如何更加充分的利用点云数据分布特征来构建索引,使树具有更好的平衡性,是未来的研究目标。
