结合形态描述和直方图特征改进的点云配准

黄 鹏,丁海勇,刘春雷

(1.南京信息工程大学遥感与测绘工程学院,江苏 南京 210044； 2.南京龙测测绘技术有限公司,江苏 南京 210031)

1 引 言

目前,三维激光扫描技术已被广泛应用于各种场景的测量与三维重建。使用三维激光扫描技术可快速获取建筑物、文物[1]、工程构件的完整几何信息,便于后续测量处理。但在实际扫描过程中,由于扫描对象所处的位置及自身的形状遮挡了光线,无法得到扫描对象的完整点云,只能获取对象表面部分点云信息[2]。利用点云配准技术可以将不同角度获取的点云数据进行配准,从而得到扫描对象的完整点云。

目前广泛应用的点云配准算法是Besl等提出的迭代最近点(Iterative Closest Point,ICP)算法[3]。但该算法对配准点云的初始位置依赖性较强,初始位置较差会陷入局部最优状况,导致配准效果不佳。为避免上述情况,有学者采用粗配准与精配准相结合的策略。利用特征描述符来获取点与点的对应关系进行粗配准,如点特征直方图(Point Feature Histograms,PFH)[5]和快速点特征直方图(Fast Point Feature Histograms,FPFH)[6]、以及方向直方图(Signatures of Histograms of Orientations,SHOT)[7]等。采用特征点与特征描述符相结合的方法,以提高点云配准效率。如李仁忠等将ISS(Intrinsic Shape Signatures)特征点和FPFH相结合[8]；李宇翔等将ISS特征点和SHOT特征描述符相结合[2]；荆路等将SIFT(Scale Invariant Feature Transform)特征点和FPFH特征描述符相结合[9]；刘雷等将SIFT特征点与BSHOT(Binary Signatures of Histograms of Orientations)特征描述符相结合[10]。这些配准方法具有较好的整体配准效果,但这些方法中使用了SIFT法提取特征点或利用SHOT、FPFH特征描述符进行SAC-IA粗配准,均会导致配准时间较长。

针对点云配准过程中配准效率和精度无法兼得的问题,本研究提出一种将内部形态描述ISS特征点和二进制方向直方图BSHOT[11]特征描述符相结合的改进的点云配准算法。该方法先对点云进行体素格网下采样,再采用ISS算法提取特征点,降低点云数量。然后对ISS特征点计算SHOT局部特征描述符,并将其转化为二进制的BSHOT方向直方图特征描述符,再采用随机采样一致性算法(RANSAC)去除误匹配点对,获得点云配准的初始变化矩阵。最后利用改进的ICP算法进行精配准,即将传统ICP的输入值改变为源点云特征点与整体目标点云进行点云配准。

2 特征点算法

2.1 形态描述特征点

特征点是指通过一定的数学运算和标准获取具有丰富信息、稳定且独特的点集,其数量远小于原始点云数量。内部形态描述ISS提取特征点是利用邻域内协方差矩阵的特征值之间关系来选取具有代表性和稳定性的点集。主要计算过程如下[2]:

(1)对点云数据每个点pi建立局部坐标系。搜索半径区域为r内的所有点pj,计算其与中心点pi的距离权值wij,如式(1):

(1)

(2)计算pi与邻域内所有点pj的协方差矩阵cov(pi),如式(2):

(2)

(3)计算cov(pi)特征值,从大到小排序为λ1、λ2、λ3,并设定阈值ε1、ε2(其值均小于1),若满足式(3)关系,则该点为ISS特征点:

(3)

2.2 直方图特征描述

3D特征描述符中SHOT是较为先进、描述性较好的直方图特征描述符。但由于SHOT最终的向量特征整体维度较高(352维),会导致在后续配准中耗时较长,降低配准效率。因此将352维的SHOT直方图向量特征转化为352位的二进制数表示的BSHOT直方图特征描述符。该方法不仅大幅度减少内存空间的占用率,而且使计算复杂度降低,可提高后续配准的计算效率。将SHOT特征描述符转化为BSHOT特征描述符,主要是将352维的SHOT特征描述符按4个为一组进行二进制转化[11]。设SHOT特征描述符为{S0,S1,…,S351},每四个为一组分为A1,A2…A88,每组的和为Ssum,则转化规则如下[12]:

①若A中任意Si=0,则对应的Bi也为0;

②当A不满足①时,若存在Si大于90 %的Ssum,则对应的Bi=1,其余为0;

③当A不满足①和②时,若存在Si+Sj大于90 %的Ssum,则对应的Bi=Bj=1,其余为0;

④当A不满足①、②和③时,若存在Si+Sj+Sk大于90 %的Ssum,则对应的Bi=Bj=Bk=1,其余为0;

⑤若A对于①～④均不满足,则任意Si所对应的Bi均为1;

⑥将88个组的Bi组合成352位的BSHOT特征描述符{B0,B1,…,B351}。

3 点云配准

点云配准过程分为两部分:粗配准和精配准[13]。粗配准常用于位置未知的情况,对两片点云进行配准,获取较好的位置姿态,为精配准提供良好配准环境。而精配准是在粗配准基础上进行二次配准,使点云在配准后误差达到最小。

3.1 粗配准

在粗配准中结合形态描述ISS法和BSHOT直方图特征完成粗配准。两者的结合一方面可以降低点云配准时所需的数量,另一方面可减少后续配准点相似性计算的复杂度。

在计算配准特征的相似性时,常用欧式距离来衡量。但本研究采用汉明距离计算相似性确定匹配点对。通过对二进制数值进行简单的异或运算,统计结果为1的个数,总数即为汉明距离。当汉明距离最小时,可认为对应的两个特征点为同一匹配对。汉明距离的计算如式(4):

(4)

式中,d为汉明距离；x和y表示两片点云中对应的BSHOT直方图特征描述符；⊕表示异或运算,即相同则为0,不同则为1。

由于点云的稀疏性、噪声等影响,仅采用汉明距离计算相似性匹配容易形成错误匹配对。为避免此类情况,研究中也引入随机采样一致性(RANSAC)算法去除点云中错误的匹配对,从而估计初始变化矩阵。

3.2 精配准

传统的点对点ICP配准算法中,可分为两种情况:(1)未使用特征点时,将全部的源点云数据与目标点云数据进行点与点的计算配准,但该方法由于是全部点云参与计算,其配准精度较高,但耗时较长。(2)引入特征点时,采用两片点云的特征点作为参与值,其配准速度较快,但精度不如使用全部点云配准效果好,易受特征点影响。

因此在ICP精配准中本研究将上述两种方法结合形成一种新的改进的ICP算法,即在精配准过程中,源点云使用特征点,而目标点云使用全部点数据,作为ICP配准的输入值。该方法既采用了特征点的代表性又结合了全部点的整体性,一方面可保留一定的配准精度,另一方面也可减少参与配准的点云数量,使配准时间缩小。

3.3 配准过程

点云配准流程图如图1所示。

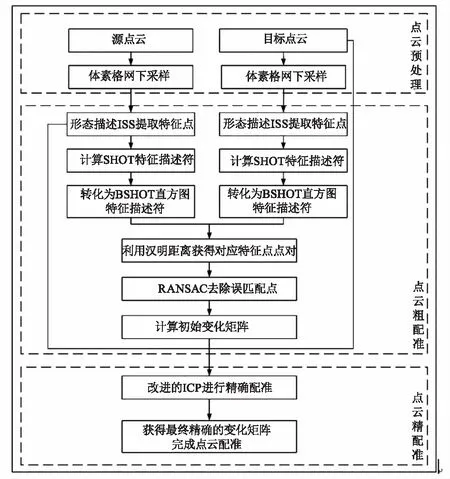
图1 点云配准算法流程

研究中的点云配准其主要过程为:①使用体素格网对初始点云下采样,减少点云数量。②使用形态描述ISS提取方法提取特征点。③使用SHOT特征描述符对特征点进行描述。④使用二进制转换规则将SHOT特征描述符转化为BSHOT直方图特征描述符。⑤使用汉明距离寻找对应的特征点点对。⑥使用RANSAC剔除错误特征点点对,获取初始变化矩阵。⑦使用改进的ICP算法进行迭代配准,获取最终精确变化矩阵,完成点云配准。

改进的配准算法在粗配准时采用BSHOT直方图特征描述符和汉明距离相似性度量方法,相比于传统的SAC-IA算法可减少配准时间。因此基于配准时间较短的基础上,采用改进的配准方法可提高点云最终配准的精度,形成一个较高效率性与精确性共存的点云配准算法。

4 实验与分析

4.1 实验数据

实验数据采用斯坦福大学扫描的Bunny数据、Armadillo数据和Dragon数据,三组点云数据如图2。实验平台为Intel(R)Core(TM)i7-10700 CPU@2.90GHz处理器,16G运行内存,操作系统为Windows10 64位操作系统,编译环境为Visual Studio 2017 C++,并结合第三方工具开源点云库PCL1.9.。

图2 原始配准点云图

4.2 实验结果与分析

由于三组点云的数据量较大,bunny数据共35,947个点,armadillo数据共172,974个点,dragon数据更是高达437,645个点。而大量点云会降低配准效率,因此实验过程中先进行体素格网下采样,再提取关键点来降低点云数量,提高点云配准效率。

为验证算法的高效率性与精确性,将所提出算法与文献[10]的SIFT+BSHOT算法、文献[8]的ISS+FPFH+SAC-IA算法、以及ISS+SHOT+SAC-IA算法进行对比。为更好对比实验,控制体素格网下采样和关键点提取的点云个数保持一致。对三组点云,四种算法进行点云的粗配准结果如图3所示。

图3 四种算法的粗准结果图

本文算法在精配准中使用改进的ICP精配准方法,其余三种对比算法采用传统的点对点ICP配准方法。为确保实验算法的可比性,精配准中相关参数设置一致。对三种不同数量点云,利用四种算法进行精配准。为便于体现最终效果的差异,我们仅截取局部区域(Bunny的嘴部；Armadillo的右臂；Dragon的头部)进行显示,其结果如图4。

图4 四种算法的精配准局部结果图

为验证配准精度,通过计算配准后两点云间的均方根误差RMSE对比不同算法的精度,RMSE的计算如式(5):

(5)

式中,N表示点云总数；T表示最终变化矩阵；pi和pj分别表示源点云与目标点云。

不同算法对点云的配准效果不同,本研究在配准精度和时间两个方面进行量化对比评估,表1、表2、表3分别代表三组不同数量点云的配准结果统计表。

表1 Bunny点云数据的不同算法配准效果评估表

表2 Armadillo点云数据的不同算法配准效果评估表

表3 Dragon点云数据的不同算法配准效果评估表

将不同算法配准效果评估表中的精配准均方根误差和配准时间用直方图表示,可明显对比其精确性和高效性,如图5所示。

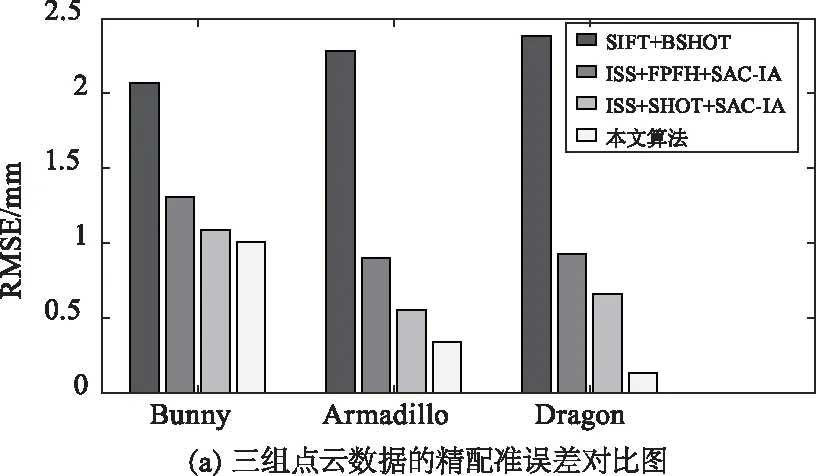
图5 四种算法配准效果对比图

从配准结果图、效果评估表和效果对比图分析可知:

(1)在特征点提取方面。本文算法采用ISS特征点提取方法,相较于SIFT+BSHOT算法中的SIFT提取方法具有较大的优势。从表1～表3中两种特征点提取的时间可得出同样结论,在提取相同个数的特征点时,ISS特征点由于其计算的简洁性,使得所耗费时间远小于SIFT特征点。

(2)在配准精度方面。本文算法基于BSHOT特征描述符采用汉明距离、RANSAC算法进行粗配准,从表1～表3可知其粗配准精度不如对比算法中SAC-IA方法的精度。原因为SHOT特征描述符转为二进制BSHOT直方图特征描述符时,存在一定程度的信息缺失。另外从图5(a)中可知,本文所提出的点云配准方法提高了点云的最终配准精度。尤其对于点数较多的点云集,其精度提高效果会更好。从表1～表3中的精配准均方根误差可知,对于三种不同数量的点云:Bunny、Armadillo、Dragon数据,本文所提出的方法相较于对比算法中精度最高的算法(ISS+SHOT+SAC-IA算法)的RMSE分别提高了0.08 mm,0.11 mm,0.53 mm。对于Dragon数据,其精度提高了约80.3 %。

(3)在配准时间方面,从图5(b)中可知,无论是点云数量较少的Bunny数据,还是Armadillo数据,或是数量较多的Dragon数据,本文算法的总配准时间均少于其余三种配准算法的配准时间。但随着点云数量的增加,其配准效率优势也会减弱。从表1和表3可知本文算法与对比算法中耗时最少的算法(ISS+FPFH+SAC-IA算法)的时间相比,Bunny数据配准时间减少了4.204 s,但对于Dragon数据本文算法在时间方面仅减少了0.899 s。

对比分析可知,本文算法在配准耗时上,比其余三种算法效率更高、时间更短。且算法中将形态描述ISS与BSHOT直方图特征以及改进后的ICP算法结合,其最终的配准精度也均高于其余算法精度。这证明了本研究所提出的配准算法同时具备较高的效率性与精确性。

5 结 语

针对点云配准过程中配准效率和精度无法兼得的问题,本研究提出一种新的点云配准算法。该算法基于内部形态描述ISS特征提取和BSHOT直方图特征配准的快速性,再结合改进的ICP算法进行精确配准。通过对不同数量点云数据(Bunny数据、Armadillo数据和Dragon数据)进行实验对比,结果表明所提出算法在配准精度和时间方面均高于SIFT+BSHOT算法、ISS+FPFH+SAC-IA算法、以及ISS+SHOT+SAC-IA算法。说明本研究提出的算法在点云配准方面具有较高的精确性与效率性,且当点云数量较多时,其配准精度的提高效果会有所增强,但配准效率的优势会减弱。