废塑料薄膜分层振动分选机理及参数优化
2023-03-02李永波杨先海王婷张启铄张宗素
李永波,杨先海,王婷,张启铄,张宗素
(山东理工大学 机械工程学院,山东 淄博 255049)
塑料薄膜大量地应用于工业包装、家庭日用品包装、服装包装、药品包装、农业包装和种植等领域。回收的废塑料薄膜是各种塑料的混合物,由于特性相近不易分选,如果混在一起不加以分选,各自的性能不同其用途也不同,将严重影响回收利用效果和价值,如低纯度分选的废塑料薄膜可再生制作包装架类廉价制品,高纯度分选出的废塑料薄膜的回收利用价值是低纯度废塑料薄膜的5~10倍。在现阶段真正制约废塑料高效回收利用的瓶颈环节不是最后的加工或再生阶段,而是废塑料的分选阶段。如果说只有优质再生才是回收废塑料的必由之路,那么首先就要分选,因为在二次加工过程中,必须采用性能一致的原料才能生产出高质量的产品。
对风选、浮选、电选等废塑料薄膜分选机理和技术的研究虽然取得了一些成果,但利用这些方法回收塑料的纯度较低,且存在污染严重,分选塑料类型单一,处理工艺复杂,相关分选配套设备数量多、能耗高、投资大等缺点。随着废塑料污染的日益严重和“双碳”经济的发展,废塑料的再生利用逐渐被重视起来。废塑料薄膜混合物多以PP、PVC和PET等成分为主,可以利用分选技术将其分离便于进一步回收利用[1-5]。区别于光选、电选等复杂的分选技术,振动分选技术是一种经济、高效、节能、环保的新型技术[6]。文献[7]对影响粮食清理设备振动体制的振动方向角进行了研究,文献[8]对废塑料薄膜风力振动分选技术及设备进行了深入研究。在研究分选机理的基础上,文献[9-12]又对分选参数和结构参数进行了优化分析。但目前的废塑料薄膜分选装置还存在着结构复杂、尺寸庞大、不经济适用等问题。本文提出了废塑料薄膜分层振动分选技术,以期能优化分选结构尺寸参数,提高分选效率。
1 废塑料薄膜振动分选技术研究
回收的废塑料薄膜是混合物,可以利用分选技术将其分离成单一种类的塑料,便于进一步回收利用。振动分选,即在振动床的振动中将物料进行分离,而这里所说的振动指的是振动床面的往复运动。齿轮齿条机构、凸轮机构、曲柄滑块机构虽然能实现废塑料分选的动作要求,但从分选功能、分选效率、机构可调节性角度分析,这些结构均不符合本研究的要求。
在已知的机构中有多种类型的机构可以将旋转运动转化为往复运动[13],曲柄摇杆机构可实现复杂运动轨迹,又具有急回特性[14],有利于振动方向角的选择,因此选择曲柄摇杆机构作为振动分析运动执行机构最合适。
振动床机构运动简图如图1所示。废塑料薄膜混合物输送到床面上,曲柄OP在主轴的带动下作旋转运动,AB平行且等于CD,曲柄中心O与连杆在筛体上的铰接点E的连线即筛子的振动方向,通过连杆PE带动床面做周期性运动。由于曲柄OP回转半径远小于连杆PE长度,所以床面运动可以近似看成沿床面方向上的简谐运动。床面上的废塑料薄膜在重力、惯性力和摩擦力等多个力作用下与床面做相对运动,由于混合物中各种废塑料薄膜摩擦系数不同,在合适的参数下使得各种废塑料薄膜产生的位移方向各不相同,经过多个周期的振动,使得不同成分的废塑料薄膜逐步分离开来,最终达到分选的目的。

图1 振动床机构运动简图
设床面的运动以OE方向为正,废塑料沿床面的相对运动以沿床面向上为正,则床面的位移、速度、加速度方程分别为:
x=-rcosωt,
(1)
(2)
(3)
式中:r表示曲柄半径;ω表示曲柄角速度;t表示工作时间。
不考虑废塑料间的摩擦,而以单片质点为对象进行分析。根据振动床的运动可知,当曲柄OP位于Ⅰ、Ⅳ象限时,
2nπ≤ωt≤2nπ+π/2
(4)
或
2nπ+3π/2≤ωt≤2(n+1)π,
(5)
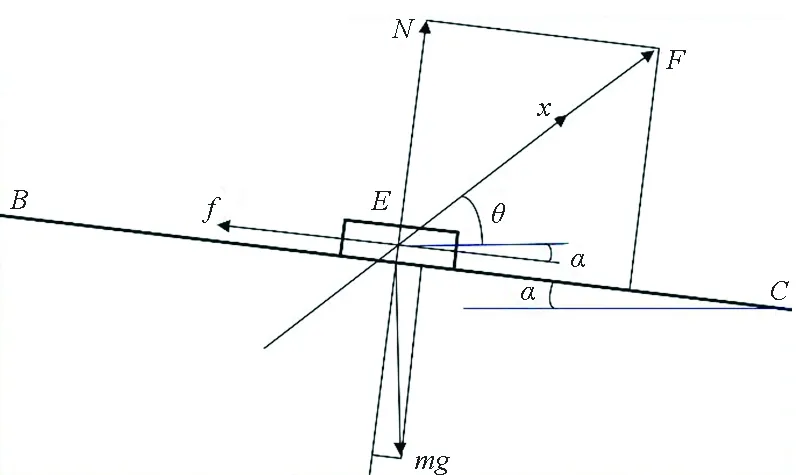
加速度aBC为正值,惯性力F为负,方向沿水平方向向左,废塑料有沿床面向上滑的趋势。废塑料在床面上的受力分析如图2所示。

图2 上滑受力分析示意图
根据达朗伯原理可得上滑方程为
(6)
化简可得
(7)
当d2xBC/dt2>0时,物料相对振动面上滑,即
(8)
令
K=ω2r/g,
(9)
上滑系数
K1=sin(α+φ)/cos(α+θ+φ)。
(10)
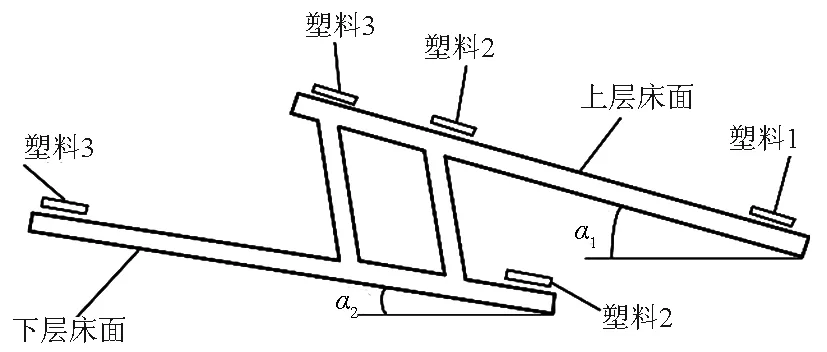
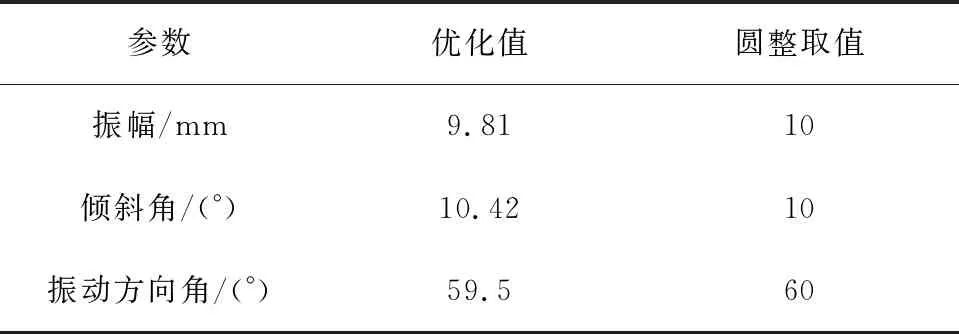
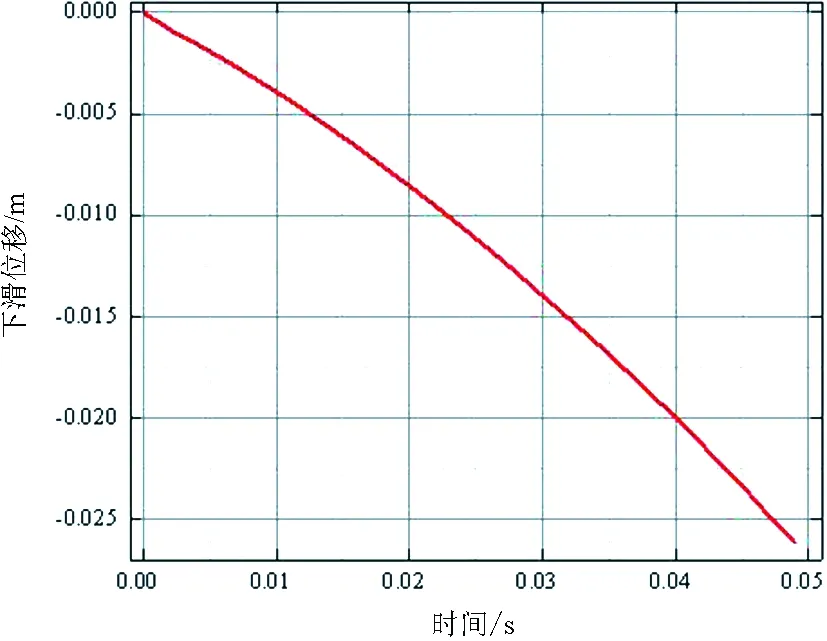
当K>K1时,废塑料将向上滑动;当K 令 (11) (12) 式中:mg表示物料自身重力;F=mw2rcoswt表示惯性力;f=μN=Ntanφ表示废塑料与床面之间的摩擦力;N表示床面法向反力;α表示床面与水平面的倾角;θ表示振动方向角,逆时针方向为正;φ表示摩擦角。 当曲柄OP位于Ⅱ、Ⅲ象限时, (2n+1/2)π≤ωt≤(2n+1)π (13) 或 (2n+1)π≤ωt≤(2n+3/2)π, (14) 加速度aBC为负值,惯性力F为正,方向沿x轴向右,废塑料薄膜有沿床面向下滑的趋势。废塑料在床面上的受力分析如图3所示。 图3 下滑受力分析示意图 同样,根据达朗伯原理有 (15) 化简可得 (16) 当d2xBC/dt2>0时,废塑料薄膜能相对床面下滑,因在Ⅱ、Ⅲ象限时,0≤cosωt≤-1,因此可得废塑料相对于床面下滑的条件为 (17) 令 (18) (19) 式中各参数同上。 废塑料薄膜在振动床面上的运动可分为上滑运动和下滑运动,恰当地选择振动床的运动振幅、频率、振动方向角和床面倾角等参数,便可以使振动床上的废塑料混合物按上述的任意一种方式或其组合的运动规律实现种类的分选。 根据废塑料在床面上的运动和受力情况,通过达朗伯原理可推导出废塑料相对床面的各种运动状态为: 按照分选要求,为分出3种不同种类的塑料,提出了如下分层振动分选技术: (1)设置上下2层床面; (2)先保证一种废塑料1在上层振动床面上有下滑运动,另外两种废塑料有上滑运动或上滑位移要大于下滑位移,分出一种塑料1; (3)将上滑的两种废塑料落在下层的振动床面上,使其中一种废塑料2在振动床面上有下滑运动分出一种塑料2,另外一种废塑料有上滑运动或上滑位移要大于下滑位移,分出一种塑料3。分选技术如图4所示。 图4 分层振动分选技术示意图 由于各种塑料摩擦系数不同,通过这种分层振动分选技术,n层床面可以分选出n+1种不同塑料。 通过得出的废塑料滑动加速度,积分推导可得出废塑料上滑和下滑的速度和位移方程。 上滑速度为 (20) 上滑位移为 (A1ωrsinωt1-B1gt1)(t1-t2), (21) 式中:t1为上滑起始时间;t2为上滑终止时间。进一步可以得出物料的下滑速度方程 vd=A2ωrsinωt+B2gt-A2ωrsinωt3-B2gt3, (22) 式中:t为运动时间;t3为下滑起始时间。进一步积分可得相对下滑位移为 (A2ωrsinωt3+B2gt3)(t3-t4), (23) 式中:t3为下滑起始时间;t4为下滑终止时间。 通过上述方程可以看出,废塑料在振动床的运动参数主要与振动方向角θ、床面倾斜角α、废塑料与床面的摩擦角φ、振动电机的转速ω、振幅r有关,其中摩擦角φ只与废塑料本身的性质有关,各种不同物质的φ取值各不相同。考虑到结构和性能设计要求,在初步设定转速ω的情况下,取方程的设计变量为 X=[x1,x2,x3]T=[r,α,β]T。 (24) 塑料振动分选机的最终分选目标是将两种或两种以上的不同塑料通过在床面上的往复运动产生的位移差将它们分离开来,因此建立的目标函数为 minf(x)=-|ΔS1-ΔS2|。 (25) 分别建立保证废塑料具有上滑运动、下滑运动、下滑位移大于上滑位移以及床面倾斜角限制、振动方向角和曲柄振幅取值范围等6个约束方程。 给定参数情况下,通过MATLAB编程计算得出优化结果。根据经验和实际工况确定参数,初步设定电机转速n=300 r/min,φ1=14.6°,φ2=21.8°,运算得出的最优化结果和圆整取值见表1。 表1 运算结果 在上述参数下,可以计算得出三种塑料的滑动状态,如表2所示。将三种塑料放置在振动床的上层床面,根据表2的三种塑料滑动状态可以看出PET处于纯下滑状态,可以从三种塑料中下滑分出,其他两种塑料处于上滑状态,不能分出种类。 表2 三种塑料薄膜的滑动状态 将上滑出的PVC和PP两种混合物流入下层床面,优化变换振动床的床面倾角α,使α=7°,再进行振动分选,可以计算得出两种塑料的运动状态,如表3所示。根据表3两种滑动状态可以看出PVC处于纯下滑状态,可以从两种塑料中下滑分出,PP塑料上滑分出。 表3 两种塑料薄膜的滑动状态 根据上面计算公式,代入优化数据,得出如图5和图6所示的PET上滑和PVC上滑位移图。 由图5可以看出上滑位移是负数,表明实际上是下滑。由图6可以看出下滑位移也是负数,表明实际上是上滑,也就是说在整个振动过程中PVC塑料既有上滑也有下滑,但上滑位移大于下滑位移,整体呈上滑状态。 图5 PET塑料上滑位移变化 图6 PVC塑料下滑位移变化 由计算得出一个周期内PET上滑位移S1=-0.018 m,下滑位移S2=0.014 m,实际下滑位移S=S2-S1=0.032 m;PVC下滑位移S1=-0.029 m,上滑位移S2=-0.014 m,实际上滑位移S=S2-S1=0.015 m;PP下滑位移S1=-0.039 m,上滑位移S2=-0.009 m,实际上滑位移S=S2-S1=0.003 m。 如果按送料下落直径0.3 m计算,床面各留出上滑和下滑距离0.3 m,则上层振动床的尺寸为0.9 m即可;如果以下落直径离出口最远位置0.6 m计算,塑料最慢约19个周期即可滑出床面,从而实现分选的目的。设计上下床面尺寸一致,考虑到上层床面上出口分选出的塑料落到下层床面中心,所以两层床面总长度尺寸为1.35 m即可;考虑到分选速度和分选过程中塑料越分散越好,宽度越宽越好,这里确定宽度为1 m。这个尺寸比其他分选方法[7]长度减少11%以上,宽度减少50%,且不需要风选系统,大大节省了分选系统的制造成本。 1)通过振动分选方案综合分析,确定了适合的振动分选机构,建立了废塑料在振动床面上的运动方程,通过恰当地选择振动床的运动振幅、频率、振动方向角和床面倾角等参数,有效控制了废塑料在床面上的运行机制,从而达到废塑料薄膜分选的目的。 2)提出了废塑料薄膜的分层振动分选技术,建立了多种废塑料振动分选的优化数学模型,得出多种不同废塑料在不同床面上分选的优化参数,使振动分选机构长度减少11%以上,宽度减少50%,且不需要风选系统,能大大节省分选系统的制造成本。


2 分层振动分选技术的提出



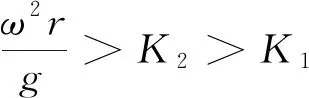
3 废塑料运动模型的建立
4 优化结果


5 振动床尺寸确定

6 结论
