考虑非共轴性的隧道开挖引起的地表沉降数值分析
2023-03-01陈洲泉陈湘生庞小朝林星涛
陈洲泉, 陈湘生, 庞小朝, 苏 栋, 林星涛
(1. 深圳大学土木与交通学院, 广东 深圳 518060; 2. 深圳大学 滨海城市韧性基础设施教育部重点实验室,广东 深圳 518060; 3. 深圳大学未来地下城市研究院, 广东 深圳 518060; 4. 深圳市地铁地下车站绿色高效智能建造重点实验室, 广东 深圳 518060; 5. 铁科院(深圳)研究设计院有限公司, 广东 深圳 518060)
0 引言
随着我国城市化进程的迅猛发展,许多大城市人口激增,地上空间建(构)筑物愈发密集,地面交通拥堵问题越来越突出,已经严重影响市民生活质量以及社会经济活动的正常运行。地下铁路建设以其运量大、效率高、空间集约等特点正成为解决城市交通拥堵问题的重要手段[1]。然而,在地铁开挖过程中势必会对周围土体造成扰动,超限的土体变形必然会影响到周围建筑物及地下管线安全。因此,合理评估隧道开挖引起的地面沉降一直是工程安全风险控制的重点和难点[2],尤其是在人口密集的城市商业圈和经济圈等地区。
值得指出的是,在地下隧道工程建设中,普遍存在着隧道开挖诱发开挖面周围应力场改变的情况。这种变化既存在应力大小的改变,也存在主应力方向的改变[3-5]。已有的模拟主应力轴旋转作用的土单元试验(如单剪[6-7]和空心圆柱环剪试验[8-10])表明,土体的力学性质会受主应力轴旋转的影响,显现出变形非共轴特性,即材料当前的主应力方向与塑性主应变率方向不一致。在通用的工程数值分析中采用的材料本构模型一般基于传统的共轴塑性理论建立,即假定塑性应变率的方向与当前应力状态方向一致,不考虑非共轴性。在一定程度上,这种对非共轴塑性的忽略,会给基于数值模拟方法获得的隧道工程设计和施工方案安全性评估结果带来不确定性,这对于变形控制要求高的隧道工程而言是十分不利的。
为了在工程计算中考虑主应力轴旋转引起的非共轴变形,首先,需要构建非共轴本构模型。为此,学者们已经开展了相当丰富的理论工作,当前非共轴塑性理论主要有以Rudnicki等[11]提出的所谓角点理论,Yu等[12]延伸的double shearing理论以及Lashkari等[13]在Mohr圆应力空间构建的圆切向流动理论。角点理论由于其表述形式的一般性,在后续研究中被进一步发展,形成了比较完备的体系。钱建固等[14]在考虑了第三应力不变量的影响后将该方法扩展到了更一般的三维应力状态。Li等[15]、Tsutsumi等[16]以及陈洲泉等[17-19]将这类非共轴理论与各向异性本构模型相结合,很好地模拟主应力旋转试验中土体的非共轴力学行为。
其次,在采用非共轴模型对具体工程问题开展数值模拟方面,与本构理论研究相比,相关的数值研究在广度和深度上显得明显不足。Yang等[20-22]较早地将角点型非共轴模型应用于具体工程问题的数值分析,比较了共轴与非共轴模型在分析浅基础地基承载力和变形问题上的差异,指出不考虑非共轴塑性的计算结果偏于不安全;另外,还分析了非共轴塑性对仓筒问题中主应力轴旋转和土压力分布所产生的影响。Yuan等[23]则在double shearing理论框架下发展了二维应力状态下各向异性非共轴模型,分析了地基承载问题。然而,将非共轴模型应用于隧道工程分析的案例屈指可数。只有袁冉等[24]将文献[23]发展的各向异性非共轴模型应用于隧道开挖诱发地表沉降问题的分析。
考虑到这方面工作的缺乏,笔者针对隧道开挖问题进一步开展了探究。与袁冉等[24]的工作相比,本文的创新之处在于采用了截然不同的非共轴本构模型框架和模型数值积分算法。本文采用了基于一般应力状态构建的角点型非共轴本构模型,既适用于平面应变情况,也适用于一般三维情况;其次,区别于文献[24]中采用的基于误差控制的自动划分子增量步的显式方法,本文采用了半隐式数值积分算法。通过将模型数值实现,针对隧道开挖问题,从主应力轴旋转、塑性区发展以及地表沉降等方面,比较共轴与非共轴模型计算结果的差异,进一步提高对此类问题的认识。
1 角点型非共轴本构模型
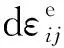
(1)
(2)
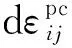
(3)
或
(4)
(5)
式(3)—(5)中:Cijkl为非共轴张量;sij=σij-δijσkk/3为应力偏张量;hn为非共轴模量,表征应力增量引发非共轴塑性变形的难易程度。hn可以在共轴模型参数确定后,通过拟合单剪试验应力应变曲线以及旋转角变化曲线来获得。
(6)
式中:rij为塑性流动方向;Q为塑性势函数; dλ为塑性标量因子。在这里采用考虑双曲硬化法则的Drucker-Prager模型来定义共轴塑性行为,该模型的屈服函数f和塑性势函数形式Q为
f=q-η(p+ccotφc);
Q=q-ptanψ。
(7)
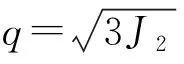
(8)
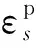
参考HS模型[25]中弹性模量的定义方法,本文中剪切模量G同样采用应力相关的形式
(9)
式中:Gref为参考剪切模量,即p=pref时的剪切模量;pref=100 kPa为参考压力。
体积模量K为
(10)
式中ν为泊松比。
2 本构模型的数值实现
本文采用Moran等[26]提出的半隐式积分算法。这种算法在应力更新过程中,塑性标量因子为隐式表达,塑性流动方向则为显式表达。这意味着在1个增量步中,塑性标量因子要在增量步中求解,而塑性流动方向在增量步初始即已给定。
2.1 应力更新算法
在ABAQUS/Standard计算平台下,1个计算增量步的应力更新过程为根据增量步给定的应变增量dεij来计算应力增量dσij。根据式(1)和(2),对于任意增量步时刻tn到tn+1的应力更新格式为
(11)
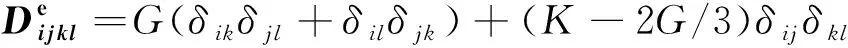
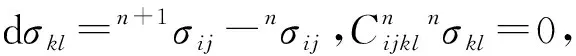
(12)
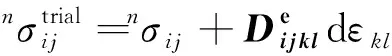
(13)
值得指出的是,方程组(13)包含了11个式子,式中与对应的未知量构成方程组解向量X,表示为
X=(n+1σ11,n+1σ22,n+1σ33,n+1σ12,n+1σ21,n+1σ13,
n+1σ31,n+1σ23,n+1σ32,n+1η,dλ)。
(14)
指定方程组(13)对应的残差向量为R(X),在采用Newton-Raphson迭代法求解该非线性方程组时,该残差向量的Jacobi矩阵可表示为∂R(X)/∂X,这是一个11×11的方阵,其形式为
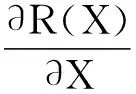
(15)
2.2 一致性刚度矩阵
由于ABAQUS/Standard分析模块采用隐式平衡迭代方法求解平衡方程,在构造平衡迭代的刚度矩阵时需要提供与应力更新过程相适应的刚度矩阵,即一致性刚度矩阵。该刚度矩阵的定义为
(16)
结合式(13)可得:
(17)
(18)
(19)
(20)
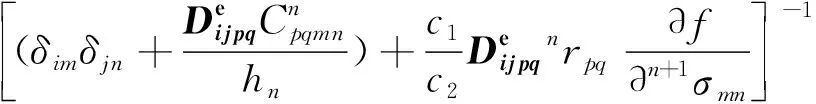
2.3 数值算法验证
在ABAQUS/Standard分析模块中,基于用户材料子程序开发接口UMAT,编写文中介绍的非共轴模型的应力积分算法,并通过模拟单剪试验的过程来验证算法的有效性以及模型描述非共轴变形的能力。单剪有限元分析模型采用单个减缩积分平面应变单元CPE4R。本构模型参数的选取参考HS模型中黏土的取值,如表1所示。

表1 模型参数Table 1 Model parameters
试验加载方式如图1(a)所示,竖向压力保持不变,σ22=500 kPa,初始静止侧压力系数K0=0.5,在单元上边缘施加水平位移实现剪切过程。
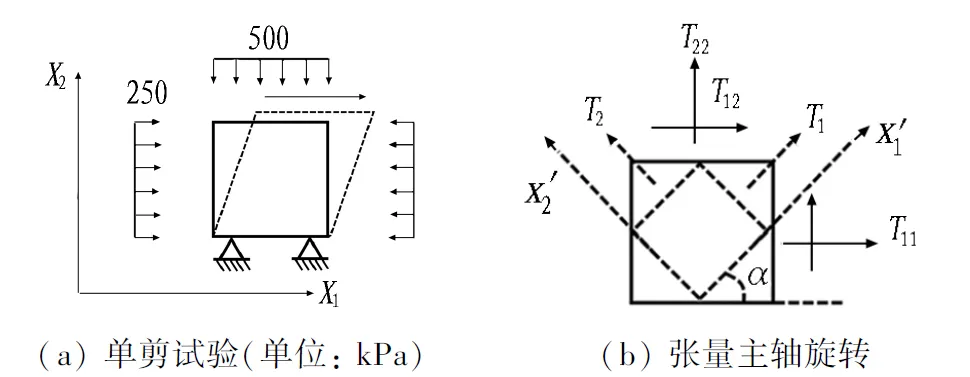
图1 单剪试验和张量主轴旋转Fig. 1 Simple shear test and rotation of principal axis of tensor
以应力和应变张量为代表的张量Tkl主轴的旋转过程可以用图1(b)中坐标系的旋转过程表示。求解张量主轴方向的过程在数学上就是对与张量对应的实对称矩阵进行对角化处理的过程,其形式为
(21)
ABAQUS内置的命令能够实现该对角化过程。这里规定主轴方向需要逆时针旋转坐标系的情况为正,顺时针为负,且旋转角的取值范围为[-180°,180°]。图2和图3展示了共轴和不同非共轴参数下模拟单剪试验的应力应变关系和非共轴角变化关系。这些结果比较好地验证了半隐式算法在程序实施时的有效性,并且保证了计算结果能够符合非共轴模型反映的力学特性。
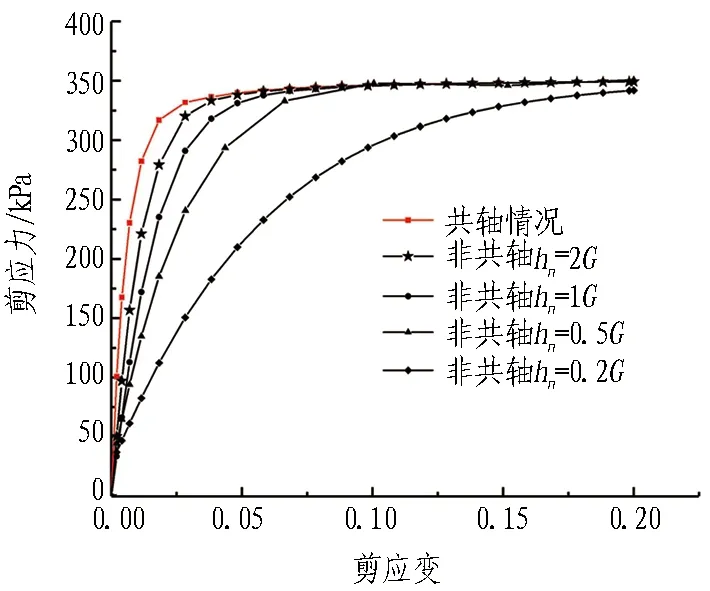
图2 应力应变关系Fig. 2 Relationship between shear stress and shear strain
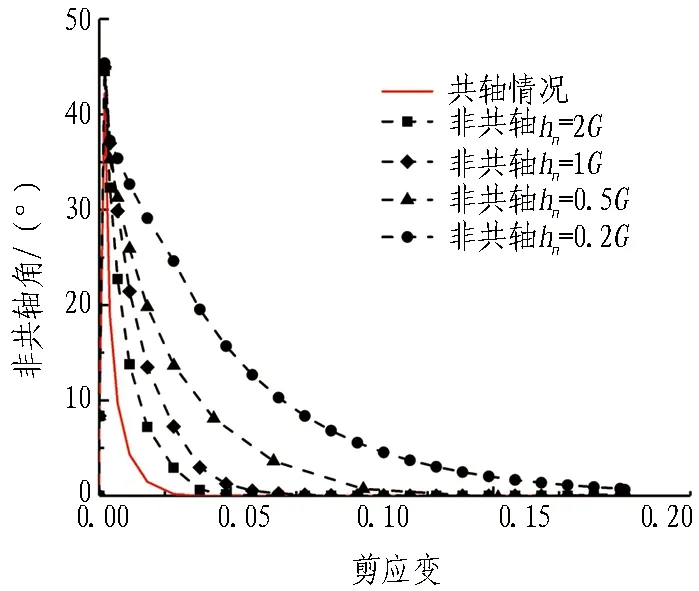
图3 非共轴角的变化Fig. 3 Variation of non-coaxial angle
3 本构模型的数值实现
3.1 有限元分析模型
本文建立了平面应变条件下模拟半无限空间黏土地层中隧道开挖过程的有限元模型,如图4所示。
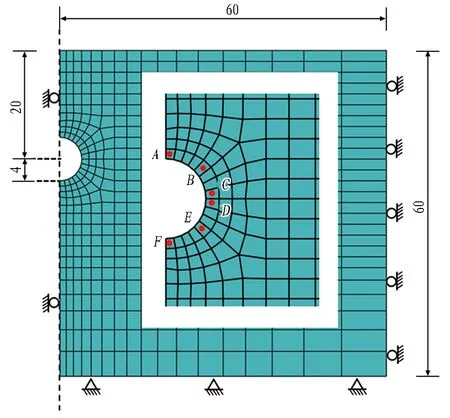
图4 隧道模型尺寸及网格划分(单位: m)Fig. 4 Geometry and finite mesh of tunnel model (unit: m)
图4展示了计算区域土体的有限元网格,考虑研究问题的对称性,取模型的一半,即尺寸为60 m×60 m。土体的有限元网格划分选用4节点平面应变完全积分单元(CPE4)。圆形隧道中心位于土体表面以下20 m位置,半径为4 m;衬砌支护厚度为300 mm,采用平面应变不可压缩完全积分单元(CPE4I),衬砌与隧道开挖面用tie连接。衬砌采用弹性模型,弹性模量E=19 GPa,泊松比ν=0.2,重度γ=25 kN/m3。在隧道周围选取6个土体单元作为监测点(A,B,C,D,E,F)。
模型分析过程分为3步: 1)地应力平衡。首先,约束模型左右两侧竖向边界的水平位移和底部位移。整个土体施加重力,重度γ=20 kN/m3。然后,模型内部定义沿竖向线性分布的地应力为σv=γH(H为隧道中心距土体表面的竖向距离),水平地应力为σh=K0σv(K0为静止土压力系数,取为0.5)。在这一步杀死衬砌单元,隧道范围内的土体单元不杀死。2)应力释放。这一步利用初始平衡态获取开挖区域土体对于开挖边界的支反力代替开挖土体的支护作用,通过释放部分支反力的方法来模拟土体稳定后的地层损失。因此,这一步将开挖区域的土体单元杀死,并在隧道边界节点处施加节点荷载,该节点荷载衰减为平衡态节点力的50%。 3)施加衬砌。激活衬砌单元,并将节点荷载衰减为0,开挖完成。
3.2 考虑非共轴性的主应力轴旋转对隧道开挖的影响
隧道开挖必然会对周围土体产生扰动。这种扰动包括土体塑性区发展的范围和程度、应力应变场大小和方向的重分布。土体扰动引起的地表沉降和隧道收敛变形是实际工程中能够直接而且准确监测到的响应,能在一定程度上反映开挖影响。下文将针对非共轴变形特性这一土体力学性质的差异对于隧道开挖引起土体扰动的影响进行讨论。
3.2.1 塑性区发展
图5展示了共轴和非共轴模型条件下隧道开挖后周围土体塑性区的分布情况。图中采用应力比表征土体的塑性发展程度。图5彩图展示了土体塑性发展程度的分布情况,应力比的取值为0.75~1。图中红灰2色图展示了应力比大于0.75(红色区域)的区域分布,即发生塑性屈服的区域。由图可以看出: 开挖会引起隧道腰部土体塑性的显著发展,沿斜上和斜下2个方向发展出2条塑性带,形成交叉式分布;离隧道开挖区域越近,塑性发展的程度越深。土体考虑非共轴性后,随着非共轴塑性模量的减小,2条塑性带沿着各自的方向向更远处延伸;同时,在2条塑性带所夹的区域中也发展出更多的塑性区。
图6展示了隧道周围6个监测点在隧道开挖过程中的应力路径变化。由于在不同非共轴参数条件下的计算得到的应力路径变化规律大致相同,所以选取了具有代表性的塑性模量hn=0.5G的情况与共轴情况进行比较。图中标注字母的位置为开挖的起始点,每条曲线上标注的点号代表开挖过程中应力释放阶段与施加衬砌阶段的交接处。图中斜直线的斜率为0.75,直线以下的区域为弹性区。由图6可以看到所有应力路径的起始点都位于直线附近,表明计算的初始状态正确。整个开挖过程中,隧道顶部(A)和底部(F)都处于卸载状态,即始终处于弹性区,这与图5中塑性区分布规律是相符的。塑性区土体(B,C,D,E)的应力路径主要在开挖的应力释放阶段发生塑性屈服,进入施加衬砌阶段,B,E的应力路径没有显著变化,但C,D的应力路径使得土体的应力比减小,即发生弹性卸载。值得注意的是,发生塑性屈服的土体的应力路径在共轴和非共轴条件下的差别较大,处于弹性状态的则差别较小。
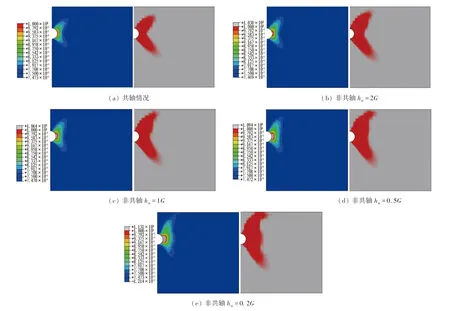
图5 塑性区分布情况Fig. 5 Distribution of plastic parameter
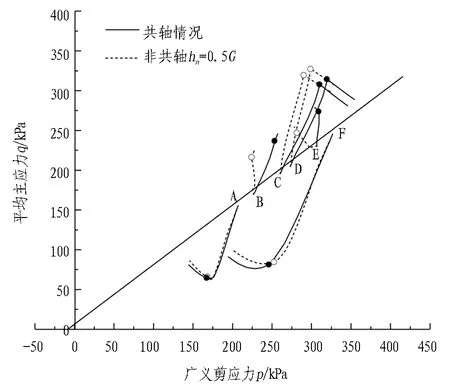
图6 监测点的应力路径Fig. 6 Stress paths at monitoring points
3.2.2 应力主轴的旋转
图7和图8展示了共轴和非共轴模型不同参数条件下隧道开挖后土体应力旋转角和剪切应力的分布情况,图中旋转角的取值范围为[-5°, 90°]。由图可见: 应力旋转发生在隧道顶部和底部,并且在隧道顶部的地表以下以及如图5所示的2条塑性带与弹性区交界的区域也都有显著的应力旋转发生;而隧道腰部土体的应力旋转现象不显著。同时,随着非共轴塑性模量的降低,模型计算得到的主应力旋转区域越广,旋转程度也越大。与应力旋转分布相对应的是,在隧道周围发生显著应力旋转的区域同时伴随着显著的剪切应力集中发展现象,并且随着非共轴塑性模量的降低,剪切应力集中发生区域向外延伸,与应力旋转区域大致重合。这与剪切应力引起主应力旋转这一论述相符。

(a) 共轴情况 (b) 非共轴hn=2G (c) 非共轴hn=1G (d) 非共轴hn=0.5G (e) 非共轴hn=0.2G图7 应力旋转角分布情况(单位: kPa)Fig. 7 Distribution of rotation angle of stress (unit: kPa)

(a) 共轴情况 (b) 非共轴hn=2G (c) 非共轴hn=1G (d) 非共轴hn=0.5G (e) 非共轴hn=0.2G图8 剪切应力分布情况(单位: kPa)Fig. 8 Distribution of shear (unit: kPa)
图9展示了隧道开挖过程中监测点处应力旋转在计算增量步中的变化情况。从图中可以看到,在2个分析步结束位置,隧道周围区域共轴模型与非共轴计算得到的应力旋转情况相差不大。值得注意的是,土体的应力旋转主要发生在开挖的应力释放阶段;而在衬砌施作阶段,监测点A,B,C,D,E的应力旋转角基本保持不变,点F则发生较大程度的应力旋转。根据各监测点土体应力旋转的方向和大小,各处的大主压应力基本同隧道轮廓线平行。比如: 隧道正侧面C,D点的应力在整个开挖阶段都没有发生显著的应力旋转,基本保持竖直向上的方向。这与图7和图8展示的分布规律相符。
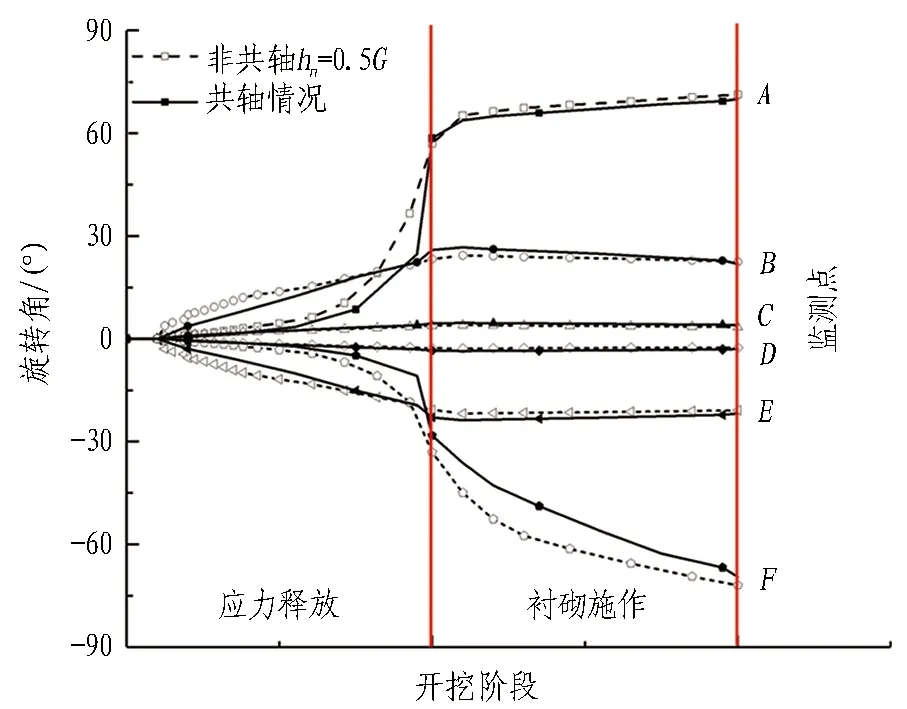
图9 开挖过程中监测点处的应力旋转变化Fig. 9 Stress rotation at monitoring points during excavation
3.2.3 地表沉降和隧道收敛变形
3.2.3.1 地表沉降
图10展示了在共轴和非共轴情况下隧道开挖的应力释放阶段和完成阶段的地表沉降曲线。由图10可以发现: 在模型条件相同的条件下,开挖完成的沉降曲线(图10(b))比应力释放阶段的曲线(图10(a))低;随着非共轴模量的减小,地表沉降曲线的沉降槽更深,且各曲线都是在离对称轴线足够远处才相交重合。
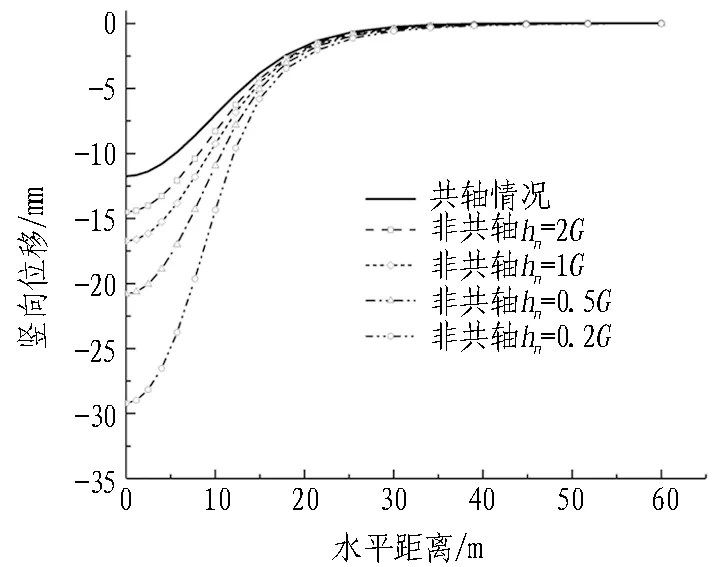
(a) 应力释放阶段
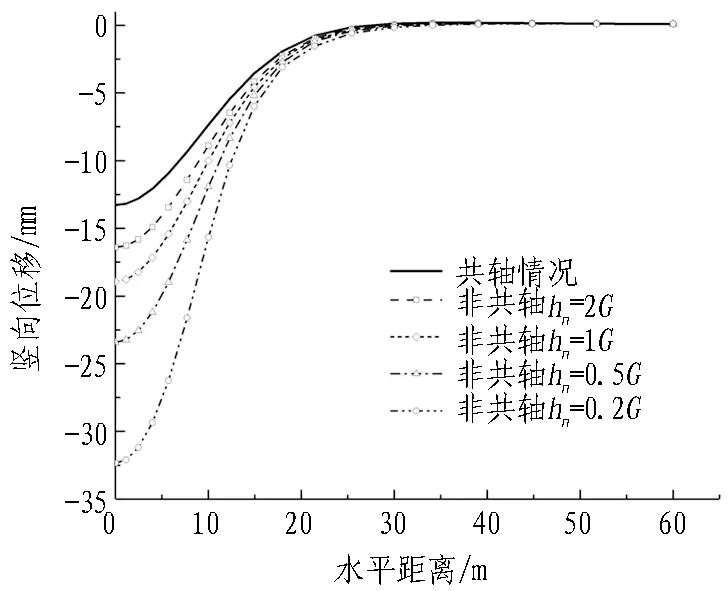
(b) 开挖完成阶段图10 开挖完成时的地表沉降曲线Fig. 10 Ground settlement curves at end of excavation
图11进一步总结了图10中各曲线斜率沿水平距离的变化规律。特别值得指出的是,各曲线斜率的最大值(曲线反弯点)在距离对称轴7.7~10 m的区间取得,即沉降曲线的沉降槽宽度也处于该区间。表明非共轴塑性模量对地表沉降槽宽度的计算结果影响较小。根据O′Reilly等[27]归纳的沉降槽经验公式
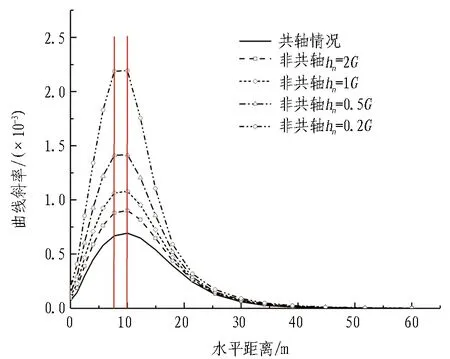
(a) 应力释放阶段
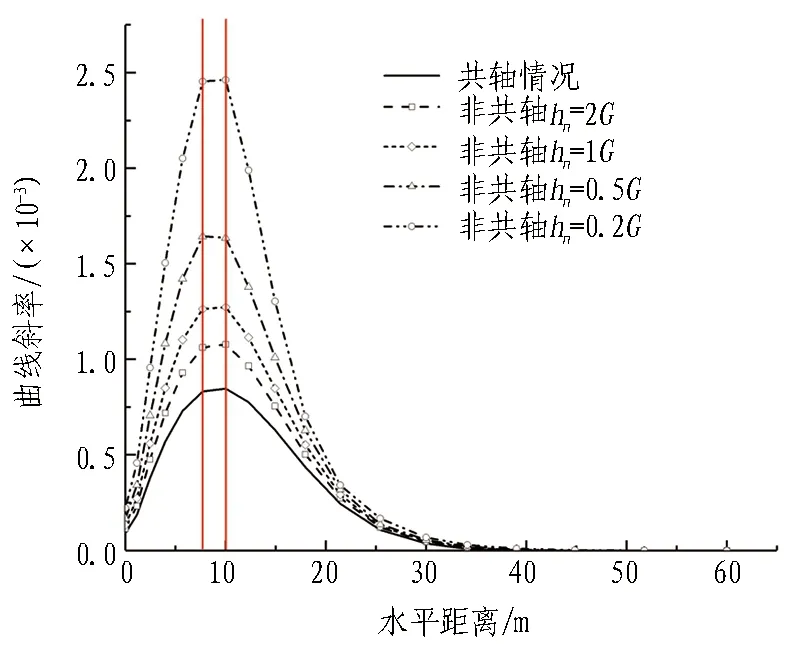
(b) 开挖完成阶段图11 沉降曲线斜率沿水平距离的变化Fig. 11 Slope of ground settlement curves along horizontal distance
i0=S0H。
(22)
式中:i0为沉降槽宽度;S0为经验系数(黏土取0.4~0.7,砂土取0.2~0.3);H为隧道中心到地表的距离。本文沉降槽宽度的经验取值为8~14 m,与计算结果相当接近,表明了数值模拟结果的合理性。
3.2.3.2 隧道收敛变形
图12比较了开挖2个阶段中不同模型参数计算得到的隧道收敛变形差异。图中隧道收敛变形是将隧道边界点位移放大40倍后得到的结果。从图12可以看出: 在开挖的2个阶段中,模型非共轴参数主要影响隧道顶部和侧面向内的收敛变形,不影响隧道底部的向上位移;同时,当模型非共轴模量小到一定程度(如0.2G),土体对隧道侧向的作用要大于对隧道顶部的作用,表现为隧道出现侧向压扁的倾向。对比图12(a)与(b)可以看出,衬砌施作后,由于隧道管片的自重较大,隧道表现为竖向进一步受压的倾向。因此,隧道竖向收敛变形的程度相对于应力释放阶段进一步加剧;而隧道侧向被挤出,横向收敛程度小于应力释放阶段。
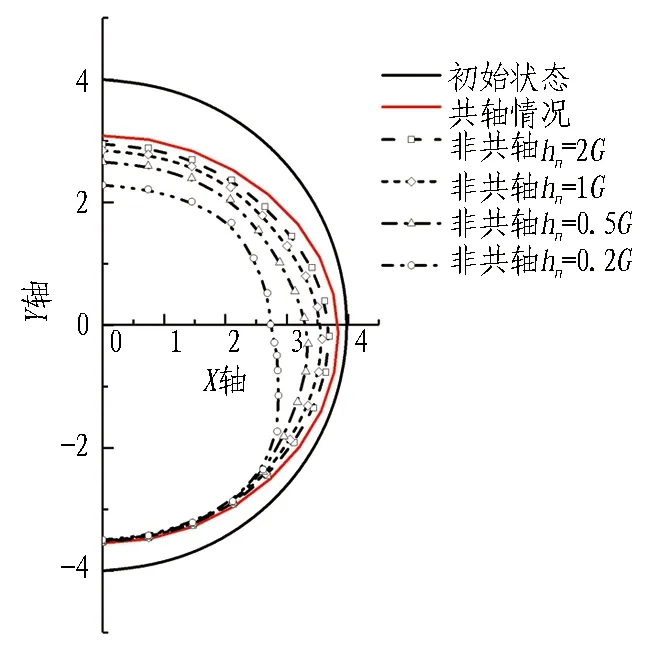
(a) 应力释放阶段
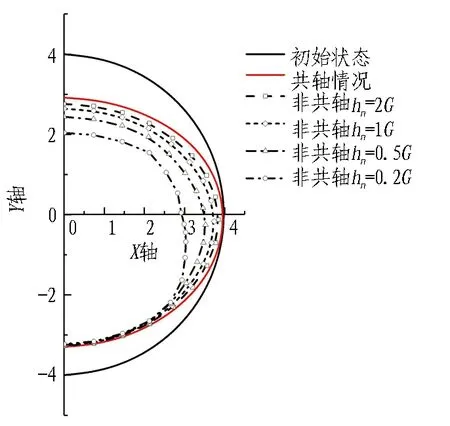
(b) 开挖完成阶段图12 隧道收敛变形Fig. 12 Convergence of tunnel
4 结论与建议
采用半隐式应力更新算法,编写了考虑双曲剪切硬化的DP模型的非共轴模型用户材料子程序UMAT。在ABAQUS/Standard的分析模块中模拟半无限空间地层内衬砌隧道开挖过程,并针对非共轴性对隧道开挖的影响进行参数分析,得到以下结论。
1)隧道开挖过程会引起隧道腰部周围土体沿斜上和斜下2个方向发展出2条交叉的塑性带。考虑非共轴变形后,模型的非共轴塑性模量越小,这2条塑性带延伸的越远,同时2条塑性带所夹区域发展出更多塑性区,而对于隧道顶部和底部的土体则一直处于弹性阶段。
2)开挖过程中土体的应力主轴方向的改变是一个渐变的过程,开挖面周围土体的大主压应力方向由竖直方向逐渐向隧洞轮廓线形状靠拢。同时在2条塑性带上下外缘与弹性区也存在显著的主应力旋转,模型的非共轴变形越强,主应力旋转的区域和程度也越大,这表明隧洞顶部和底部弹性区的土体沿塑性带向隧道移动更多。
3)本构模型的非共轴效应越强,隧道开挖引起的最大地表沉降值越大,地表沉降曲线的沉降槽越深。但是,非共轴性并不显著影响沉降槽的宽度。同时,更大的地表沉降也与土体内斜向上塑性带向地表更广地延伸,以及更大范围的隧道上部应力旋转区。
4)隧道收敛变形中,顶部和侧面向隧道内收敛变形的程度会随模型非共轴塑性模量的减小而增大,而非共轴性对于底部位移的影响较小。
总体来讲,与主应力旋转现象密切相关的非共轴变形特性会显著影响隧道变形分析的结果,是变形预测研究中不可忽视的重要因素,值得开展更深入的研究。
