基于变形稳定时间统计的挤压性围岩隧道二次衬砌施作时机研究
2023-03-01刘志春安志飞
李 雷, 朱 超, 刘志春,*, 安志飞, 李 宁
(1. 中铁第一勘察设计院集团有限公司, 陕西 西安 710043; 2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室, 河北 石家庄 050043; 3. 道路与铁道工程安全保障省部共建教育部重点实验室(石家庄铁道大学), 河北 石家庄 050043; 4. 中国铁路设计集团有限公司, 天津 300143)
0 引言
随着我国西部基础设施建设的推进,挤压性围岩大变形问题已成为困扰隧道建设者的突出难题。挤压性围岩是在高地应力环境下,隧道周边一定范围内产生显著塑性变形或流变的岩体,具有高地应力、低强度、强流变的显著特征[1]。在高地应力作用下,挤压性围岩隧道极易产生大变形,从而造成支护开裂、钢架扭曲、变形侵限甚至衬砌开裂掉块现象[2-3]。
在大变形条件下,二次衬砌施作过早或过晚均会影响到隧道施工安全和结构稳定,因此,二次衬砌施作时机始终是挤压性围岩隧道研究的热点问题[4-9]。一般隧道二次衬砌需待初期支护变形稳定后施作,此时初期支护承受全部围岩荷载,二次衬砌为安全储备。而对于挤压性围岩隧道,如果二次衬砌施作过晚,则可能造成初期支护变形过大,以致隧道失稳。但是,如果二次衬砌过早施作,又会使其承受过大荷载而引起衬砌开裂掉块,进一步影响到运营安全。刘志春等[4]以乌鞘岭隧道为例,提出不同变形级别下二次衬砌施作时机的2个判别指标,即以隧道极限位移为基础的现场量测日变形量和总变形量。刘国庆[5]对大量隧道断面二次衬砌施作前的围岩变形速率进行统计,提出初期支护基本稳定判别标准为: 双线隧道连续7 d以上的平均变形速率不大于2 mm/d,单线隧道不大于1 mm/d。王中文等[6]将Ⅴ级、Ⅳ级、Ⅲ级围岩的变形值分别达到最终变形量的80%、85%、90%时所对应的时间作为围岩变形基本稳定判别准则。王永刚等[7]基于木寨岭隧道工程的大量监测数据,将围岩水平收敛速率作为围岩变形稳定标准,并提出Ⅰ级变形收敛速率为0.5 mm/d,Ⅱ级为1 mm/d,Ⅲ级为1~2 mm/d。郭小龙等[8]提出轻微、中等和严重大变形段分别在隧道开挖45~55 d、55~60 d和80~90 d达到二次衬砌施作标准。孟陆波等[9]以鹧鸪山隧道为例,提出在初期支护变形量为最终收敛值的65%~70%后施作二次衬砌较适宜。
对隧道变形时间特征,众多学者也开展了大量研究工作。张勇等[10]根据现场监测资料对围岩变形全过程的位移-时间关系曲线进行了分析。杨会军[11]对隧道围岩收敛测量数据进行曲线分析,对变形时效特征进行了总结。左清军等[12]结合现场监测资料,根据围岩分级将围岩变形-时间特征曲线划分为3阶段的“弯弓”型和4阶段的“台阶”型。孙元春等[13]则根据围岩变形速率对围岩变形曲线进行了划分。刘学增等[14]基于现场实测数据,分析了变形稳定时间与围岩级别的关系。王睿等[15]通过概率统计对大量监测数据进行分析,得到了Ⅳ级和Ⅴ级围岩变形基本稳定时间。
综上所述,不少学者提出了以变形量和变形速率为判别指标的二次衬砌施作时机,但很少给出二次衬砌施作的具体时间范围值。
本文通过对412个挤压性围岩隧道断面变形监测数据进行统计分析,得到不同变形等级的挤压性围岩隧道变形稳定时间范围值,提出基于变形最终稳定时间的分阶段二次衬砌施作时机预测方法,以分阶段变形稳定时间作为二次衬砌施作时机的判别指标,为挤压性围岩隧道二次衬砌施作时机判别提供参考。
1 挤压性围岩变形分级标准及统计样本
1.1 变形分级标准
国内外研究学者针对挤压性围岩隧道变形分级标准进行了大量研究[2,16-19]。自20世纪末,我国西部地区修建了大量的挤压性围岩隧道,这些隧道具有相似的地质及变形特征。在工程实践过程中,基于变形分级的勘察、设计、施工理念已逐步被人们接受[20]。
根据挤压性围岩隧道地质条件及地应力等因素,目前我国挤压性围岩变形潜势等级划分标准如表1所示[1, 20]。变形潜势分为轻微、中等、严重、极严重4 个等级。表1中,岩体强度应力比Gn=Rcm/σmax,其中Rcm为岩体强度,σmax为最大初始地应力(σmax=λ0·σv,λ0为初始地应力侧压力系数,σv为垂直地应力); 相对变形ε=u/a,其中,u为围岩变形,a为隧道等效洞径。

表1 挤压性围岩隧道变形潜势等级划分标准Table 1 Classification standards for deformation potential of tunnel in squeezing rocks
1.2 样本统计
调研统计了412个挤压性围岩隧道断面收敛变形实测数据,其中,国外样本55个[21-28],占比13%; 国内样本357个[29-35],占比87%。由于多数隧道的强度应力比不详,故本文根据大变形分级标准中相对变形指标对统计样本变形等级进行划分。隧道开挖跨度按现行规范[1, 36]划分: 5~12 m为中小跨度,大于12 m为大跨及以上。
统计样本中,Ⅰ级变形断面共56个(占比14%),其中,中小跨41个,大跨及以上15个; Ⅱ级变形断面共106个(占比26%),其中,中小跨40个,大跨及以上66个; Ⅲ级变形断面共141个(占比34%),其中,中小跨33个,大跨及以上108个; Ⅳ级变形断面共109个(占比26%),中小跨73个,大跨及以上36个。具体见表2。
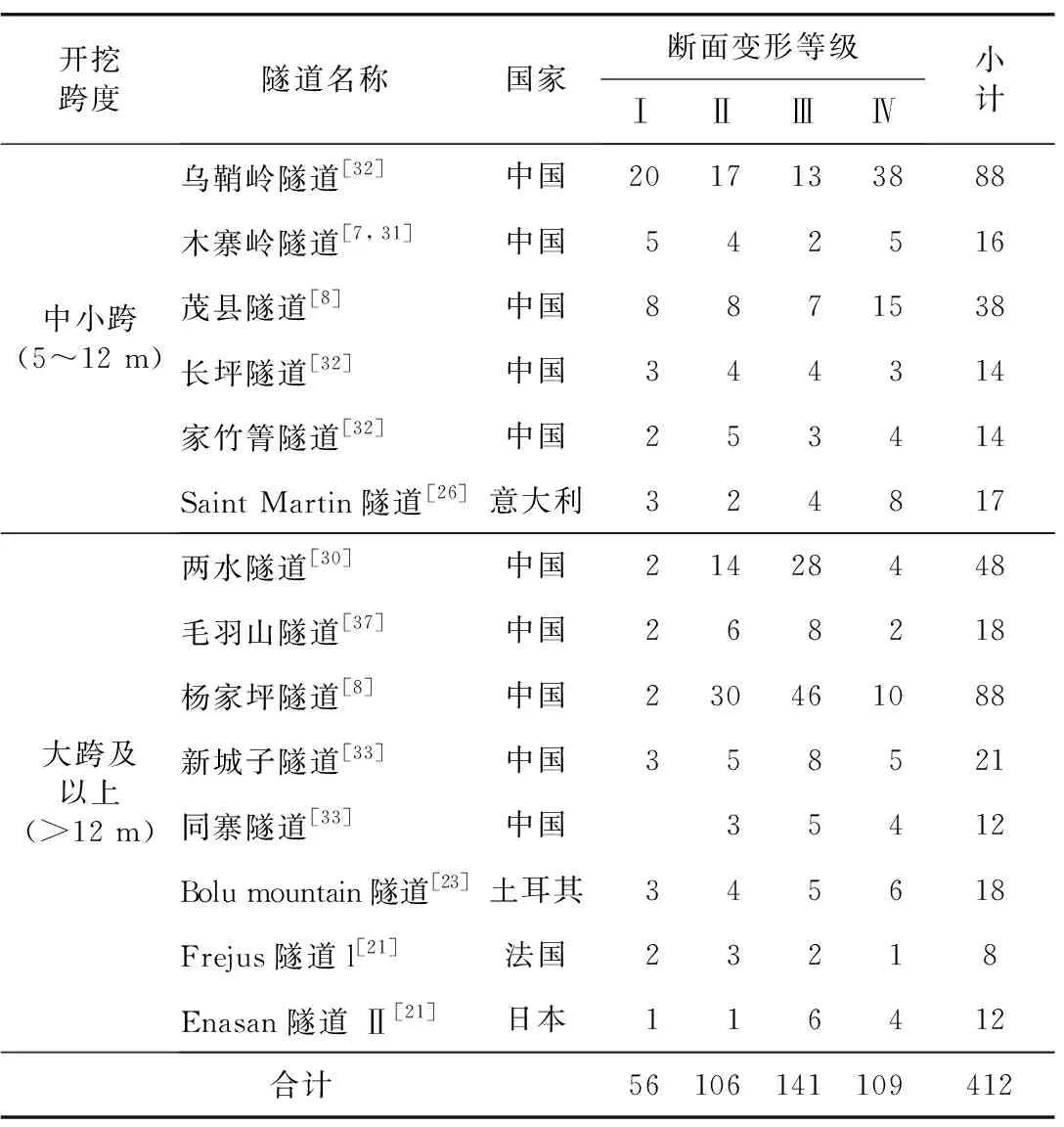
表2 变形曲线样本来源及数量汇总Table 2 Source and quantity of measured deformation curves of tunnel
2 变形数据处理方法
2.1 变形数据处理步骤
为寻求变形稳定时间与变形时间曲线的关系,对变形数据样本按以下步骤进行处理:
1)根据实测变形时程曲线特征,选取可用的拟合函数形式;
2)进行多种函数形式的曲线拟合,选取相关系数最大的函数形式为拟合曲线形式u=f(t);
3)根据变形稳定时间判据v限取值,在拟合曲线上获取变形稳定时的变形量u稳和稳定时间t稳;
4)通过统计分析,建立变形稳定时间t稳与最终相对变形ε稳的关系曲线;
5)通过统计分析,建立分阶段相对变形εt与最终稳定时间t稳的关系曲线,实现分阶段稳定时间预测,从而确定以稳定时间为判定指标的分阶段二次衬砌施作时机。
2.2 变形时程曲线拟合及稳定时间取值方法
选取某断面实测变形时程曲线,如图1所示,围岩变形经历了急速增长、缓慢变形和基本稳定3个阶段。实测变形时程曲线仅是围岩变形全过程曲线的一部分,统计样本中常规监测手段难以监测到元件埋设前和铺设防水板后的变形[4]。另外,铺设防水板后、浇筑衬砌混凝土完成前,需要重新测点,受防水板完整性要求限制,一般难以再布设测点量测变形,造成这段时间的变形也难以获取,所以曲线拟合及统计分析只针对元件埋设至铺设防水板之间的实测变形数据。

图1 隧道围岩变形时程曲线Fig. 1 Deformation-time curves of tunnel rock
图1中,围岩实测数据为元件埋设后至铺设防水板前的变形,围岩变形拟合曲线为u=f(t),变形速率拟合曲线为v=f′(t)。观察变形速率v=f′(t)曲线,t以d为单位,当变形速率明显下降并趋于缓和时,取缓和段沿时间坐标v 在一般隧道中,《铁路隧道施工规范》[38]规定二次衬砌应在围岩和初期支护变形基本稳定后施作。变形基本稳定判据为: 拱脚水平相对净空变化速度小于0.2 mm/d,拱顶相对下沉速度小于0.15 mm/d。 在挤压性围岩隧道中,上述标准已不再适用。经近年来的研究和工程实践,在《铁路挤压性围岩隧道技术规范》[1]中形成如下规定,二次衬砌施作应在围岩和初期支护变形基本稳定后进行,变形基本稳定应符合: 变形速率明显下降并趋于缓和,当无经验时,可按7 d平均变形速率小跨小于1 mm/d、大跨及以上小于2 mm/d执行,并对二次衬砌进行加强。即对于中小跨,v限=1 mm/d; 对于大跨及以上,v限=2 mm/d。经工程实践检验,按此判据施工的隧道均未因挤压变形原因而出现衬砌开裂问题。 采用最优曲线拟合法预测稳定阶段围岩变形,选取3个典型断面对变形预测方法进行说明。3个典型断面的变形时程曲线如图2所示。受各断面施工条件限制,变形时程曲线呈不同发展趋势,以变形发展最不稳定的断面1为例,基于曲线特征分析,选取5种函数形式进行拟合,如表3所示。 图2 典型断面变形时程曲线Fig. 2 Deformation-time curves of typical cross-section 表3 断面1变形时程曲线函数Table 3 Deformation-time curve function of cross-section 1 由表3可知,相关系数最大的为指数2函数形式,其他2个断面可得到同样的结果,为此,取拟合函数形式为 u=f(x)=A1+A2·e-t/A3。 (1) 式中:u为围岩变形,mm;f(x)为函数形式;t为量测时间,d; e为自然常数;A1、A2、A3为拟合常数。 为预测稳定阶段围岩变形u稳及稳定时间t稳,先根据式(1)得到变形速率曲线的函数形式,即 v=f′(x)=(-A2/A3)·e-t/A3。 (2) 式中:v为围岩变形速率,mm/d;f′(x)为f(x)的导数。 令式(2)中v=v限,可求得 t=-A3·ln[(-v限·A3)/A2]。 (3) 将式(3)求得的t值进位取整,可得稳定时间t稳。 将t=t稳代入式(2),可得稳定时围岩变形速率 v稳=(-A2/A3)·e-t稳/A3。 (4) 将t=t稳代入式(1),可得稳定阶段围岩变形 u稳=A1+A2e-t稳/A3。 (5) 断面1—3均为中小跨隧道,取v限=1 mm/d。根据式(3)—(5)计算可得断面1—3的变形预测结果,见表4。 表4 典型断面变形预测结果Table 4 Deformation prediction results of typical sections 在上述变形预测方法中,不同断面拟合曲线的A1、A2、A3有不同的取值。为建立统计意义上变形稳定时间t稳与围岩相对变形ε稳(ε稳=u稳/a)的关系,对412组t稳和ε稳数据进行统计分析。上述预测得到的t稳是以元件埋设时间为起点计算的,根据文献[4]的统计结果,隧道开挖至元件埋设的时间为1~3 d,为获得自开挖至变形稳定的时间并保证二次衬砌施工安全,在上述预测t稳的基础上增加前期丢失位移的时间3 d,即 (6) 由于中小跨和大跨及以上采用不同的变形稳定时间判据,故分中小跨和大跨及以上2种情况进行数据统计。以中小跨为例进行数据统计方法说明。在统计样本中,受现场施工环境、量测方法、停工时间等条件限制,统计数据离散性很大。187个中小跨断面变形稳定时间与对应相对变形的关系散点图如图3所示。 图3 中小跨隧道与ε稳关系散点图(剔除前数据)Fig. 3 relationship scatter chart of medium-and small-span tunnel (data before elimination) 为保证统计数据的可信度,需对异常数据进行剔除。基于表1变形分级标准,先将中小跨隧道断面相对变形分布划分为2%≤ε<4%、4%≤ε<6%、6%≤ε<8%、ε≥8%共4个区段。每区段分别按90%和10%的覆盖率作为该区段围岩稳定时间的上限和下限,将界限外的数据作为异常数据进行剔除,4个区段的上下限如图4所示。 图4 中小跨隧道各区段变形稳定时间数据处理Fig. 4 Data processing of deformation stabilization time of each cross-section of medium-and small-span tunnel 中小跨隧道剔除异常数据后的变形稳定时间与相对变形的关系散点图如图5所示。 图5 中小跨隧道与ε稳关系散点图(剔除后数据)Fig. 5 relationship scatter chart of medium-and small-span tunnel (data after elimination) 对于225个大跨及以上隧道断面采取同样的方法剔除异常数据后,得到大跨及以上隧道变形稳定时间与相对变形关系散点图,如图6所示。 图6 大跨及以上隧道与ε稳关系散点图(剔除后数据)Fig. 6 relationship scatter chart of large-span and above tunnel (data after elimination) 将中小跨和大跨及以上隧道变形稳定时间与相对变形关系散点汇总,结果如图7所示。 图7 围岩最终与ε稳关系散点图Fig. 7 Final relationship scatter chart of surrounding rocks 表5 不同变形等级的变形稳定时间(二次衬砌施作时机)统计结果Table 5 Statistical results of deformation stabilization time (construction timing of secondary lining) of various deformation levels 由表5可见,中小跨和大跨及以上挤压性围岩隧道各等级变形稳定时间范围相差不大,变形稳定时间与相对变形呈正相关。由表5可初步确定二次衬砌施作时机,如在设计阶段预测某区段变形等级为Ⅲ级,隧道跨度为中小跨,则二次衬砌需要在开挖72~107 d施作。 表5中不同变形等级的变形稳定时间,是按2.3节中“1 mm/d和2 mm/d”的判据,通过实测变形曲线拟合预测而得到的变形稳定时间。在这些实际工程中,有部分隧道(如乌鞘岭隧道)二次衬砌施作时间短于表5所列时间[4],这些隧道因初期支护强度不足又过早施作了二次衬砌从而导致了二次衬砌开裂等现象。实际工程中,不同隧道存在着支护刚度及控制措施的差异性,变形发展变化规律也不尽相同,具体操作时应先通过表5统计数据初步估算二次衬砌施作时间,再采用后续4.1节施工期分阶段二次衬砌施作时机预测方法,根据实测变形曲线进行预测取值。 另外,变形稳定时间与施工处治原则(以抗为主、以让为主和让抗结合)是紧密相关的,表5中统计数据是通过表2统计样本而获得。表2中除早期中国的家竹箐隧道、法国的Frejus隧道、日本的Enasan隧道部分区段采用以抗为主原则,中国的毛羽山隧道部分区段采用以让为主(超前导洞释放)原则外,其余统计样本均采用让抗结合原则。以抗为主和以让为主均会使变形稳定时间更长。 实际工程中,很难在设计阶段对围岩变形进行准确预测,而且实际工程中隧道的变形等级也不易获得,同时一般情况下铺设防水板后不再继续量测变形。在这种情况下,如仍以变形速率为判别指标,则在施工过程中很难确定二次衬砌的合理施作时机。 图8 施工期不同阶段与ε稳关系散点图Fig.8 relationship scatter chart of various stages in construction period 表6 基于稳定时间统计的施工期分阶段二次衬砌施作时机预测方法Table 6 Prediction method of construction timing of secondary lining by stages in construction period based on stabilization time statistics 选择隧道变形量测断面对表6所示的基于变形稳定时间统计的分阶段二次衬砌施作时机预测方法进行应用检验。 表7 施工期分阶段二次衬砌施作时机预测方法检验结果Table 7 Test results of prediction method for construction timing of secondary lining by stages during construction period 由表7可知,YDK176+641断面20、30、40 d及稳定时的预测变形稳定时间分别为76.8±22 d、72.6±18 d、70.4±15 d及67.3±13 d,实际最终稳定时间62 d均在以上4个区间范围值内,其中稳定时的预测变形稳定时间与实际变形稳定时间最为接近,20、30、40 d及稳定时中位值与实际值62 d的误差分别为23.9%、17.1%、13.5%、8.5%,预测误差值可被工程所接受。 2)采用指数函数u=f(x)=A1+A2·e-t/A3可以充分反映挤压性围岩隧道变形时程曲线特征,并取得最大拟合相关系数。 4)提出了基于变形稳定时间统计的施工期分阶段二次衬砌施作时机预测方法,可根据量测到的20、30、40 d和稳定时的相对变形,分阶段预测并最终确定二次衬砌施作时机。 由于本文统计样本中各隧道的地质条件、支护刚度、控制措施及施工方法等工程条件存在一定差异,使统计结果出现较大的范围值,具体实施时应根据工程条件合理取值。2.3 变形稳定时间判据
2.4 稳定阶段变形预测



3 基于变形分级的变形稳定时间统计
3.1 异常数据剔除方法


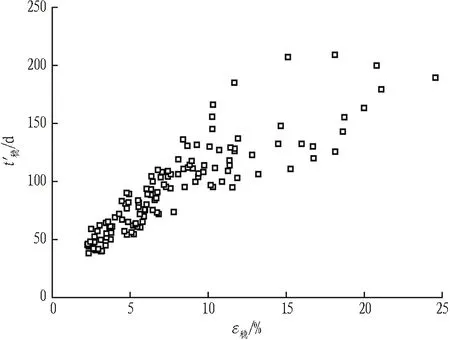
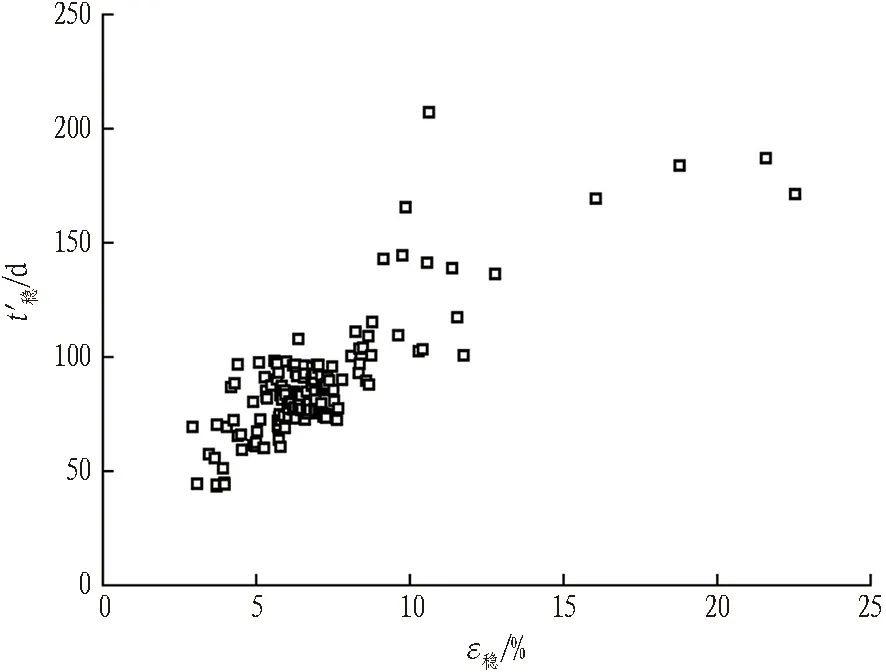
3.2 变形稳定时间统计分析


4 施工期分阶段二次衬砌施作时机预测
4.1 施工期分阶段二次衬砌施作时机预测方法
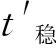

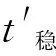

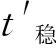
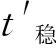
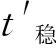
4.2 应用检验


5 结论与讨论