水液压马达定子曲线设计方法与自锁问题研究
2023-03-01于硕潘燚孙有伟聂松林尹方龙
于硕,潘燚,孙有伟,聂松林,尹方龙
(1.北京工业大学材料与制造学部,北京 100124;2.中国船舶第七〇五研究所昆明分部,云南昆明 650032)
0 前言
随着对清洁能源的不断重视以及人类环保意识的增加,水液压技术快速发展。水液压马达作为重要的执行元件,在当今的水液压系统中起着能量转化的作用。在一些空间小的工作空间,对径向柱塞马达的设计和研制有了新的要求。
水液压马达的效率和稳定性受到各种因素影响。径向柱塞马达具有体积小、扭矩大,启动效率高等优势[1-2]。而对于径向柱塞水液压马达,定子曲线的设计和制造是决定马达正常运转的关键,它直接决定着滚子与定子间的接触应力[3],以及柱塞副的运动规律等。本文作者通过分析滚子与定子接触存在的自锁问题,对压力角进行分析,并对定子曲线的设计方法和生成过程进行研究,解决接触存在的问题,保证马达在工况下平稳运转。
1 滚子与定子接触的自锁问题
针对之前加工的定子导轨进行分析,重新对定子曲线的设计方法进行研究。定子曲线的设计直接影响马达的运转情况及寿命,定子导轨的性能主要由曲线轮廓和定子的材料共同决定。图1为马达结构,图2为马达侧向视图。在马达运转过程中,柱塞向上运动使得滚子与定子的内曲面接触,并随着转子的转动,沿着定子轮廓线运动。滚子在柱塞的推动下沿着导轨面运动,导轨曲面将承受较大的接触应力,甚至会出现磨损[4],严重时会影响马达的寿命。滚子与定子内曲面的相对运动以滚子的滑动为主,在此忽略滚子自身的滚动,以滑动进行研究。定子曲线的轮廓通过压力角的大小影响滚子的滑动运动,当压力角小于接触的摩擦角时,会在接触时发生自锁。并且定子与滚子的材料配对会影响之间的摩擦因数,从而影响其相对运动情况。
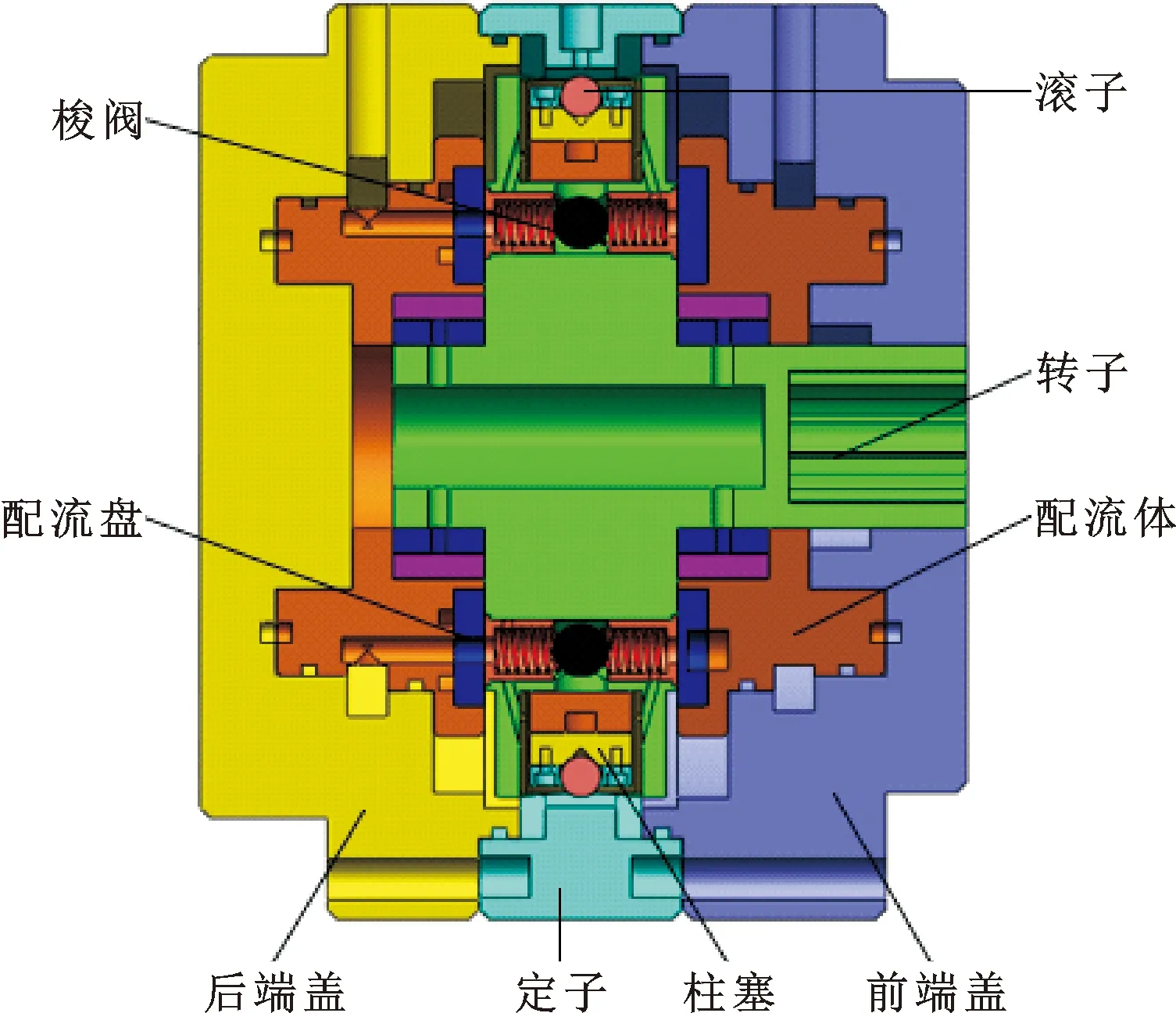
图1 内曲线式水液压马达的结构
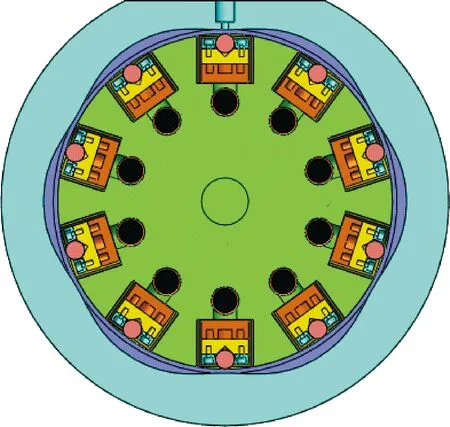
图2 马达的侧向视图
1.1 滚子的受力分析
文中的内曲线式径向柱塞马达中,滚子的材料为氮化硅(Si3N4),属于高温结构陶瓷。氮化硅硬度大,自身具有润滑性,并且耐磨损。而之前的定子曲线导轨为9Gr18不锈钢,属于耐磨、耐腐蚀的金属材料。根据文献[5-6]在液氮介质中对Si3N4/9Gr18的配对副摩擦磨损研究,常温条件下,Si3N4/9Gr18的配对副摩擦因数为0.5。
图3所示为液压马达内部的滚子与定子导轨接触示意。定子导轨的内部轮廓为定子曲线,在滚子与定子接触的时候,在垂直于接触面处存在压力。因此在接触面会存在静摩擦力,且静摩擦力与压力和压力角有关。由于定子曲线轮廓的特点,决定着滚子与定子导轨在接触时的压力角是不断变化的。对滚子与定子导轨接触状态进行研究,并对接触压力角进行分析。
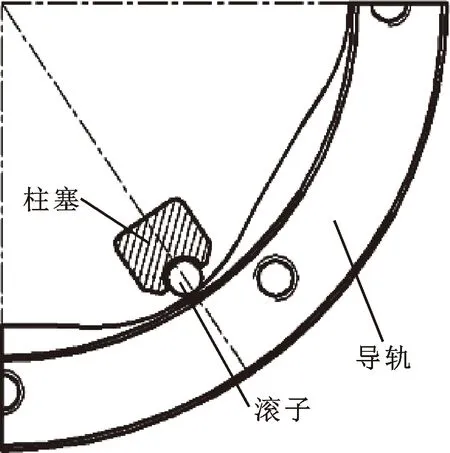
图3 滚子与定子导轨接触示意
如果作用于滚子的压力的作用线在摩擦角之内,则无论滚子受到多大的力,总会有一个与之等大的全反力和其相抵消,从而滚子会静止不动,发生自锁现象,在此情况下马达不能转动。此时涉及到定子曲线的轮廓设计问题,要保证接触的压力角大于自锁临界角。
为了进一步分析滚子与定子导轨的接触情况,对滚子的受力情况进行研究,如图4所示。滚子与定子接触的面为具有一定角度的曲面,都具有一定的压力角,可在分析固定位置时看做斜面来分析。如图4所示:F为滚子所受柱塞对其的推力,将其分解为沿斜面的力Fx以及垂直于斜面的力Fy,FN为定子对滚子的支撑力,f为滚子所受的摩擦力。根据对滚子的受力分析,对定子与滚子接触进行研究。在之前的设计中,滚子为Si3N4:陶瓷球,定子的材料为9Gr18,Si3N4/9Gr18的配对副摩擦因数为0.5。对滚子的受力进行计算,可知滚球质量为8.85×10-4kg,重力为8.67×10-3N(滚球材料为Si3N4,滚球半径r为4 mm,密度ρ为3.3 g/cm3)。而文中马达的工作压力为1~10 MPa,由于实际情况中,柱塞滚子组件所受的重力相对于此压力小之又小[7],因此在对滚子进行受力分析时将其忽略。
对图4中滚子受力进行分析:沿斜面的分力Fx=Fsinα,垂直于斜面的力Fy=Fcosα。由于FN=Fy,且摩擦力f=μFN=μFcosα。为保证滚子的运动,只有当Fx>f,即sinα>μcosα时才能产生沿斜面向下的加速度,使其正常运动。最终简化为滚子与定子导轨间材料的摩擦因数μ与压力角α的数值关系,即需要保证tanα>μ,才能避免自锁发生。
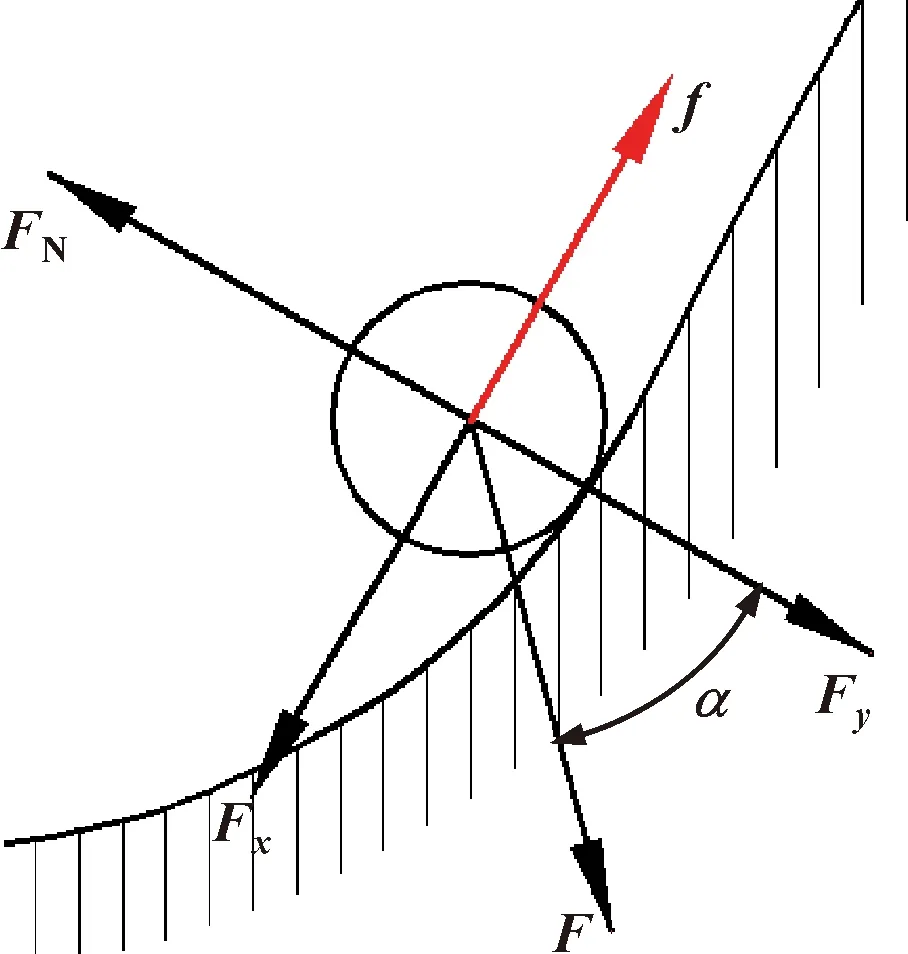
图4 滚子受力分析
1.2 解决自锁的方案设计
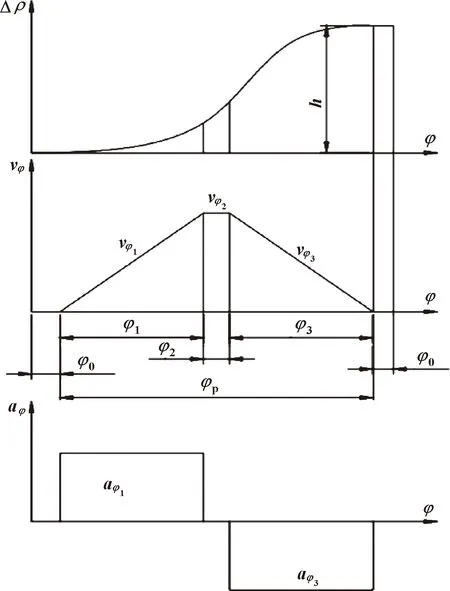
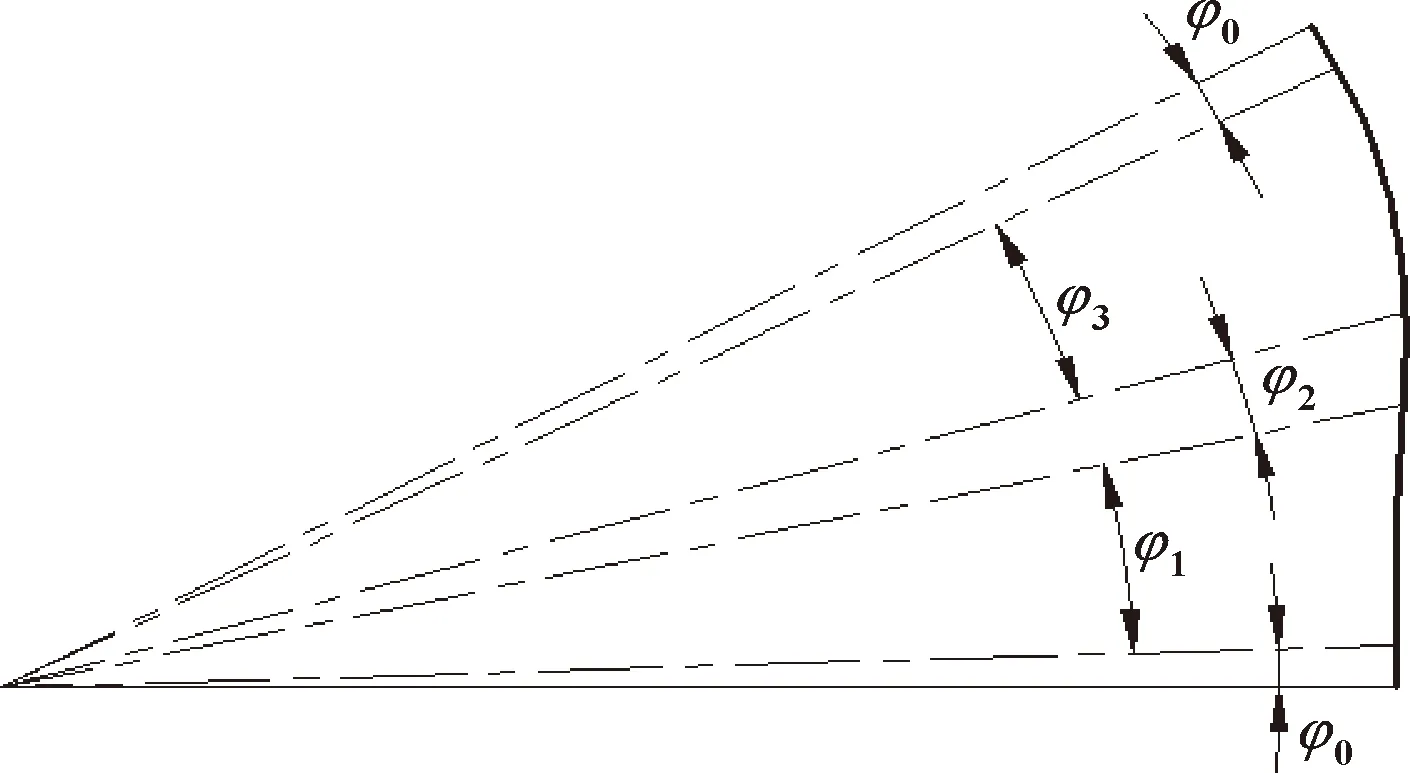
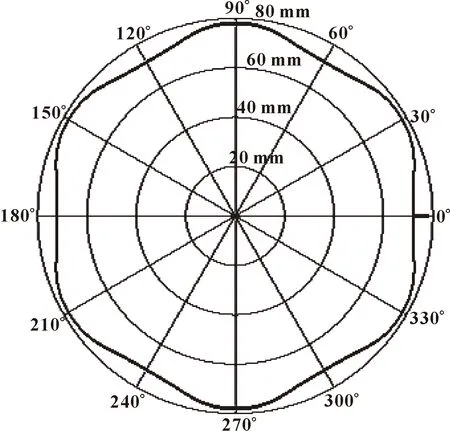
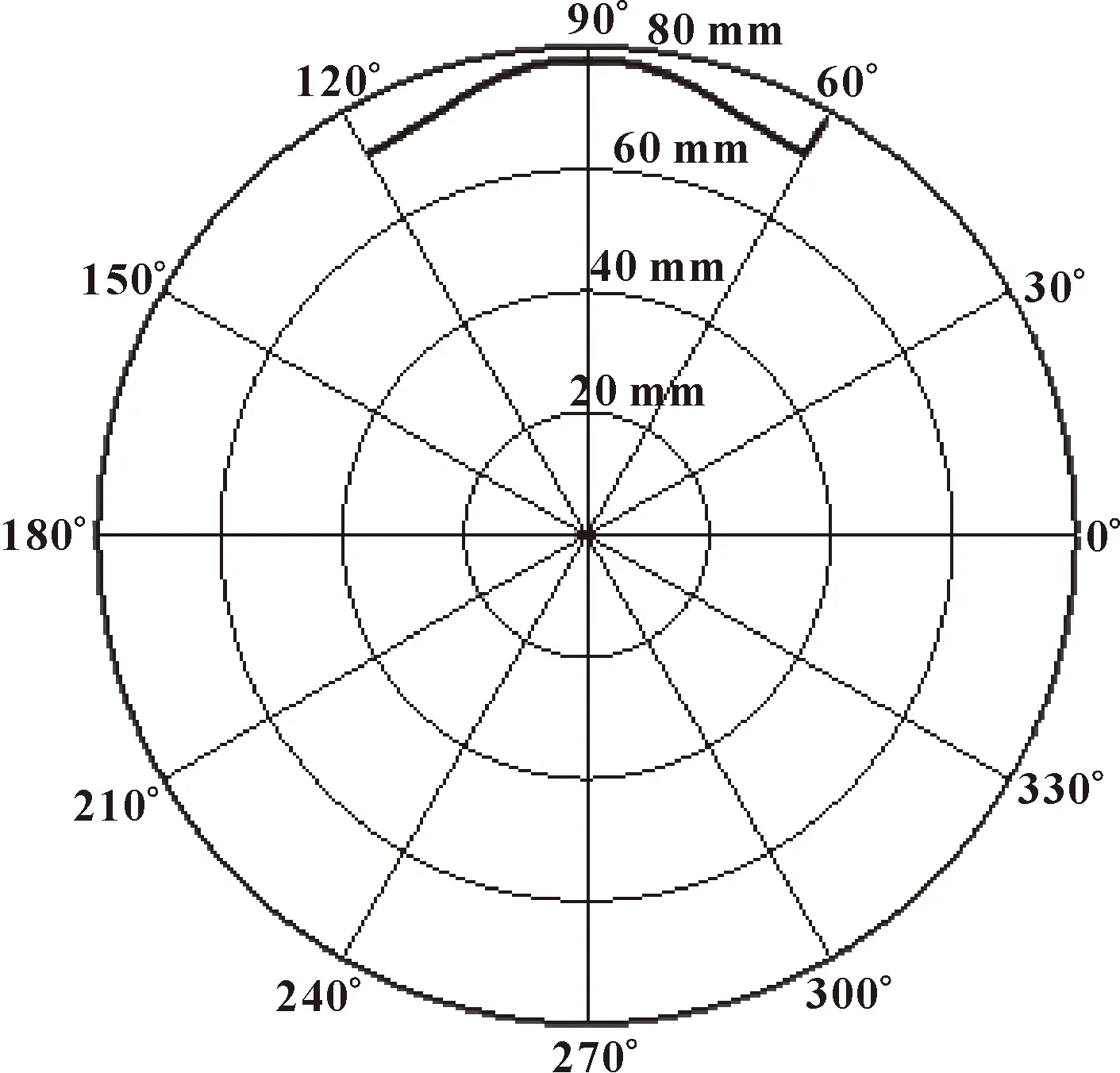
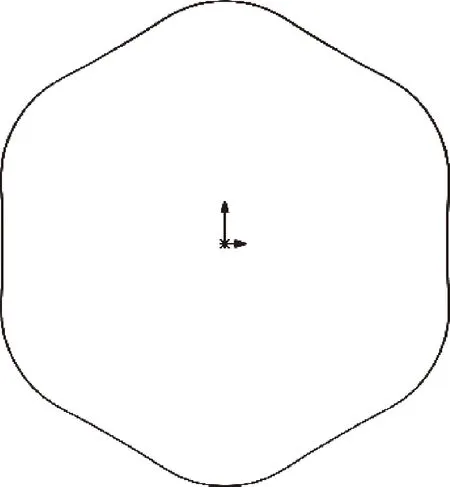
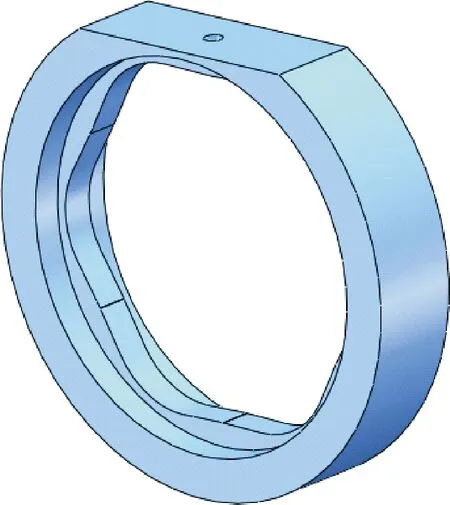
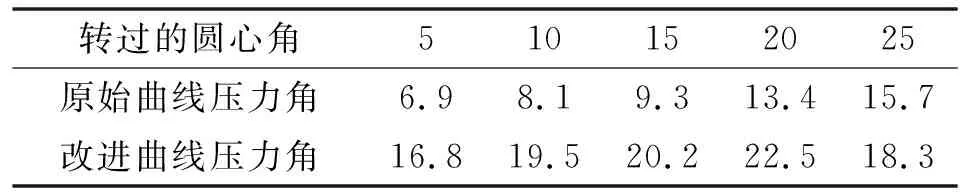
对之前定子曲线中摩擦因数μ与压力角α的关系进行分析。通过测量,压力角α的最大值为11.38°,因此sinα=0.197,cosα=0.980,μcosα=0.490。因此Fx (1)若避免自锁,使Fx>f,则sinα>μcosα,即μ (2)若避免自锁,使Fx>f,则sinα>μcosα,即μ 对两种解决方案进行分析:方案一通过改变定子的材料,从而进一步改变滚子与定子材料的摩擦因数,来避免自锁;方案二在保证定子材料不变的情况下,对定子曲线的轮廓进行改进,使滚子正常运动。作者采用方案二,通过重新设计定子曲线,改变定子导轨轮廓,从而改变接触压力角的方式,达到避免自锁的目的。如图5为改进前后的定子曲线轮廓对比,改进后的滚子与定子导轨接触的压力角有了明显变化。 图5 改进前后的定子轮廓对比 改变定子导轨的轮廓,需要重新对定子曲线进行设计。由于马达工作过程中,滚子与定子曲线相接触,为了设计出合适的定子曲线,对接触压力角有一定的要求。 图6为定子导轨的局部轮廓,在极坐标下,定子曲线的中心到定子曲线上一点的距离为极径ρ,极径与Y轴方向极角为φ。 内曲线式液压马达柱塞副的运动完全取决于定子曲线的设计。而定子曲线设计的关键在于:降低定子内表面的接触应力;减少惯性冲击,降低噪声;扭矩脉动小,输出扭矩恒定[8]。国内外在内曲线式马达的设计中,常用的定子曲线有:等加速运动规律曲线、加速度按余弦变化运动规律曲线、加速度按正弦变化运动规律曲线、加速度按抛物线变化运动规律曲线、加速度按梯形变化运动规律曲线、有等速过渡区的等加速运动规律曲线等几种类型[9]。 选用具有等速过渡区的等加速运动规律曲线对定子曲线进行设计。具有等速过渡区的等加速运动包括零速区段、加速区段、等速区段、减速区段、等速区段5个阶段。这种运动规律能充分利用幅角进行加速,加速度值较小。图7所示为具有等速过渡区的等加速运动规律曲线,分别为滚子相对位移Δρ、速度vφ和加速度aφ随转角φ在半个作用内的变化规律。在半个作用中,Δρ逐渐上升到最大位移h处,速度呈梯形趋势变化,加速度稳定。这种规律决定了马达的扭矩无脉动,转速十分均匀,软冲现象有所减小,马达的运动平稳[10]。 图7 具有等速过渡区的等加速运动规律曲线 定子曲线运动规律曲线方程 (1) 式中:φ为滚子中心绕缸体中心转过的相位角;aφ为柱塞副相对运动的角加速度;vφ为柱塞副径向相对运动的角速度;ρ为滚子到缸体中心的距离,随相位角不断变化(极径);ρ0为滚子中心最低点的极径。 等加速运动规律曲线是由“等加速-阿基米德螺旋线-等减速”曲线构成的,其中阿基米德螺旋线的使用可以使流量脉动减少或为零,起到缓冲作用,保证运转的平稳性。定子曲线的幅角分配如图8所示。 图8 定子曲线的幅角分配 根据马达转子的相关尺寸,对柱塞的行程和初始位移进行初步确定:柱塞行程h=6 mm,初始位移ρ0=72 mm。所研究的内曲线马达为六作用十柱塞,作用次数x=6,柱塞数z=10。对各区段幅角、速度等参数进行计算。 一个作用幅角: (2) 角模数(周期角): (3) 式中:m为作用次数与柱塞数的最大公约数。所研究的为六作用十柱塞径向马达,因此m=2。 零速区: (4) 加速区段: (5) 等速区段: (6) 减速区段: (7) 工作幅角: (8) 各区段运动参数,加速区段的加速度: (9) 最大速度: (10) 加速区段位移: (11) 加速区段最大位移: (12) 等速区段: (13) 等速区段最大位移: (14) 减速区段位移: (15) 通过对定子曲线的各个参数进行计算,得到滚子在定子曲线运动中每个区段对应的角速度、角加速度以及相对位移的具体值,如表1所示。在零速区段时,角速度、角加速度都为零;在加速区段结束后,具有最大的角速度,相对位移逐渐增大;减速区段结束后,角速度减小到零,相对位移增至最大。 表1 定子曲线各区段的角速度、角加速度、相对位移 由于内曲线式水压马达为十柱塞六作用马达,每个作用过程中转过60°的作用角。以60°为一个作用周期,将柱塞的运动过程划分为上升期和运动下降区各为30°。由于每个周期中柱塞的运动状态相同,因此这里以第一个作用周期为例,对柱塞的运动规律及前60°的曲线方程进行分析。 在柱塞上升过程中,滚子中心的位移方程如式(16)所示,上升过程柱塞转过30°。上升过程分为零速区、加速区、等速区、减速区和零速区。1°~13°为加速区段,13°~17°为等速区段,17°~29°为减速区段。此过程中滚子随着柱塞向上运动,并在30°时运动到最高点。 (16) 30°~60°为柱塞的下降过程,滚子中心位移如式(17)所示,下降过程柱塞转过30°。下降过程也分为零速区、加速区、等速区、减速区和零速区。31°~43°为加速区段,43°~47°为等速区段,47°~59°为减速区段。此过程中滚子随着柱塞向上运动,并在60°时运动到最低点。 (17) (1)基于MATLAB的轮廓曲线 在加工前需要对计算出的定子曲线进行验证,因此将滚子的位移公式(即定子曲线公式)利用MATLAB软件进行编程。通过相应程序运行,得到对应的定子曲线轮廓。图9所示为运行程序后0°~360°的定子曲线轮廓,径向分度值为20 mm。对之前的相关公式进行了验证,为之后定子的加工提供依据。 图9 MATLAB程序运行后的定子曲线 (2)数据点生成 选择定子曲线的1/6进行导入,即一个作用周期。通过MATLAB单独运行定子曲线的π/3~2π/3对应区段的部分程序。运行结果见图10,为定子曲线一个作用周期内的轮廓。 图10 一个作用周期内的定子曲线轮廓 在MATLAB中提取该段定子曲线上的数据点,并将提取数据的极坐标转化为直角坐标。将图形中点的坐标数据变量“s”按照X、Y、Z三列放入文本文档(二维坐标中,Z=0),将其保存成‘.txt’格式。 (3)定子导轨三维实体的生成 需要将设计的定子曲线导入到绘图软件中,实质上通过MATLAB得出的定子曲线是由大量的点组成的集合。数据点以坐标的形式导入,并且符合函数的特性,一个横坐标对应一个纵坐标,因此不能将曲线上所有的点全部导入,导入1/6的点坐标。 使用SolidWorks中的曲线功能,将之前保存在文本文档中定子曲线的坐标点数据进行插入。生成曲线如图11所示,进一步生成实体。然后通过圆周阵列,而在三维软件中得到完整的定子曲线,进一步对其做其他特征操作处理。图12为最终马达定子导轨的三维模型。 图11 三维软件中生成的定子曲线 图12 定子导轨的三维模型 对比定子曲线改进前后,柱塞转过不同圆心角时滚子与定子接触的压力角如表2所示。对比发现,改进后接触压力角有了明显的增大且均大于16.5°。 表2 定子曲线改进前后的滚子与定子接触的压力角 单位:(°) 通过对定子与滚子间自锁问题的分析,对比改进前后的压力角,并对滚子与定子导轨接触时的受力情况进行研究,提出避免自锁现象的方案。利用MATLAB对定子曲线方程进行设计和编程并提取点坐标,借助三维软件完成建模,完善了定子曲线设计过程中的不足,增大了滚子与定子导轨间的接触压力角,避免了马达滚子与定子导轨接触时发生自锁现象。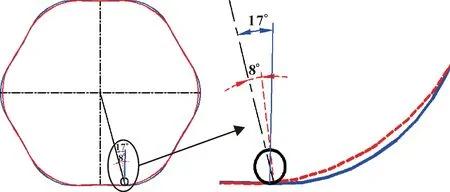
2 定子曲线的设计及方法
2.1 定子曲线类型选取
2.2 定子曲线的表达式

3 定子曲线的生成
3.1 定子曲线函数方程
3.2 定子曲线数据点及轮廓的生成
4 结论
