斯托克斯第一问题的有限差分法的MATLAB实现

摘  要：斯托克斯方程是流体力学中描述粘性牛顿流体运动的方程组，在航空航天、流体力学、化工工程、生物工程等与流体有关的所有领域都有着非常重要的作用和广泛的应用。有限差分方法通过离散物理问题，从而以代数方程式的形式来求解出误差较小的近似数值解。文章给出斯托克斯第一问题使用有限差分法和MATLAB矩阵运算的计算方法，通过对网格进行二维剖分细化，借用计算机的强大算力得出稳定性条件下的速度曲线，并使用相关算例进一步确定扩散数的阈值。

关键词：有限差分法；斯托克斯问题；MATLAB

中图分类号：TP391  文献标识码：A  文章编号：2096-4706（2023）20-0058-04

MATLAB Implementation of the Finite Difference Method for Stokes First Problem

CHEN Geng

（North Minzu University， Yinchuan  750030， China）

Abstract： The Stokes equations are a set of equations describing the motion of viscous Newtonian fluids in fluid mechanics and have a very important role and wide application in all fields related to fluids such as aerospace， fluid mechanics， chemical engineering and bioengineering. The finite difference method solves approximate numerical solutions with small errors in algebraic equation form by discretizing the physical problem. This paper gives a computational approach to the Stokes first problem using the finite difference method and MATLAB matrix operations to derive the velocity profile under stability conditions by refining the grid with a two-dimensional profile， borrowing the power of computer arithmetic， and using relevant arithmetic examples to further determine the threshold value of the diffusion number.

Keywords： finite difference method; Stokes problem; MATLAB

0  引  言

随着科技的进步和计算机技术的快速发展，在自然科学和工程计算领域诞生了许多实际问题，人们发现这些问题可以通过微分方程恰当地表示出来[1]。Stokes方程是流体力学中描述粘性牛顿流体运动的方程组，在航空航天，流体力学，化工工程，生物工程等与流体有关的所有领域都有着非常重要的作用和广泛的应用。同时Stokes问题在不可压缩流体问题的稳定性的分析上起着至关重要的作用。现如今，对于微分方程的解，可以归结为两大类，一类是精确解，另一类是数值解。由于精确解只有在一些特殊的情况下才可以求出，因此研究微分方程的数值解就变得非常重要。对于偏微分方程数值解的研究已经有很长的历史，目前应用比较广泛的方法主要有有限差分法、有限元法、谱方法等[2，3]。

近年来，Stokes问题的数值求解方法一直是国内外学者研究的热点，有限差分法是求解微分方程的一种成熟、高效的方法，其主要思想为以差商近似导数，具体步骤可分为：对方程的求解区域进行网格剖分；对微分算子进行离散；建立以网格节点上的值为未知数的代数方程组等[2]。这种方法在规范几何形状区域内误差在合理范围内且运算速度快，更具优势。MATLAB基于矩陣运算，具有强大的数值运算能力。使用MATLAB求解微分方程，近些年有大量的研究[4-7]，王忆锋等人运用有限差分法直接求解二维下的泊松方程[8]，廖臣等人则在有限差分法对偏微分方程求解下探究五点差分格式的算法[9]，巫衡竹等人使用有限差分法来求解Stokes问题的理论证明。因此探索Stokes问题新的数值计算方法及应用具有重要的现实意义。

本文探讨通过MATLAB使用有限差分法构造差分格式，从而在剖分细化的网格上求解Stokes第一问题的误差在合理范围内的数值解，并使用相关算例进行结果检验和稳定性验证。

1  斯托克斯第一问题在网格节点上的有限差分

假设有一块无限大的平板浸没在无界的静止流体中，突然以速度u0沿其自身所在的平面运动起来，并且一直保持速度的大小和方向不变。请求解平板起动后流体运动随时间的变化过程，简称为平面壁突然加速问题。

考虑Navier-Stokes方程：

选择y轴与平面壁重合并指向u0方向，由于平板是无限大的，我们假定在相同的xy平面内速度是恒定的，故?u / ?x = ?u / ?y = 0，且无外力项。由文献[10]知流场压力为常数且处于同一水平高度，故p = 0。综上简化后的Navier-Stokes方程为：

有限差分方法通过离散物理问题，对网格进行二维剖分细化，从而以代数方程式形式求解出近似数值解。接下来进行网格剖分，h表示水平步长，Δt表示垂直步长，等间距划分N×N个网格，网格节点标记如图1所示。

对函数u （z， t）做二维泰勒级数展开，写作：

将上式中的前两式相加，可得同时间t下的u对t的二阶导数，同时选取向前差分格式写出节点i的u对t的一阶导数：

代入简化后Navier-Stokes方程可得：

舍去上式中的o（Δt， h2）后整理可得：

其中j和j + 1表示時间t时刻的速度和t + Δt时刻的速度；i、i -1和i + 1表示网格细分后的节点速

度。由稳定性准则可定义扩散数条件应满足：

如果扩散数超过稳定性标准，则解的震荡误差会增大。

2  有限差分格式的求解

斯托克斯方程的边值问题的有限差分法是利用网格状模型上离散节点的数值解来逼近在时间序列下的真实解。在计算机环境允许的情况下，网格划分越细密，则节点越多，离散化模型越精确。运用MATLAB求解问题，则需将差分代数方程转化为矩阵格式：KU = B，故需将上式整理为：3  数值实验

假设在t = 0时刻之前的平板和流体均处于静止状态，随后平板开始沿着自身的平面以u0 = 15 m/s的速度运动，流体的运动粘度为α = 0.000 217 m2/s，设置步长分别为h = 0.001 m，Δt = 0.02 s或Δt = 0.002 s，由此计算斯托克斯第一问题的速度。

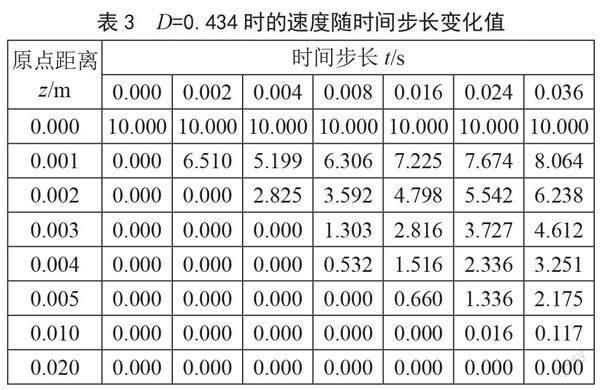
由已知数据可计算出扩散数D在两组不同的Δt步长下分别为：D1 = 4.34，D2 = 0.434，由文献[10]知D1超过了稳定性标准。本程序为更便于直观表现扩散数是否震荡，故编写图像展示如图2和图3所示。

计算结果如表2所示。

分析表3中的数值可以再次验证D1 = 4.34时的数值震荡误差较大，迭代后速度之间跳跃过大；D2 = 0.434时的数值结果符合稳定性准则。如果要减少D1的震荡误差，可适当增大网格步长h或是进一步细分时间步长Δt。

4  结  论

本文给出了斯托克斯第一问题方程的有限差分格式，利用MATLAB编制求解算法相关程序，并绘制出直观图像观察数值解是否存在震荡误差。对MATLAB程序进行数值实验，验证该方法的有效性并运用计算机的巨大算力实现有限差分法计算流体力学，大大提高计算效率。

参考文献：

[1] 吴泽康，韩文静，耿勇，等.二维二阶双曲型方程隐式差分格式的稳定性分析 [J].齐鲁工业大学学报，2023，37（1）：75-80.

[2] 陈艳萍，鲁祖亮，刘利斌.信息与计算科学丛书67：偏微分方程数值解法 [M].北京：科学出版社，2015.

[3] 戴嘉尊，邱建贤.微分方程数值解法：第2版 [M].南京：东南大学出版社，2012.

[4] 唐洪浪，桂现才.用MATLAB符号工具箱编程求常微分方程的通解 [J].洛阳师范学院学报，2005（2）：81-84.

[5] 赵德奎，刘勇.MATLAB在有限差分法数值计算中的应用 [J].四川理工学院学报：自然科学版，2005（4）：61-64.

[6] 冯立伟.热传导方程几种差分格式的MATLAB数值解法比较 [J].沈阳化工大学学报，2011，25（2）：179-182+191.

[7] 冯立伟，王选鹤，马莹.一种非定常不可压N-S方程的不等阶插值FDSD解法 [J].沈阳化工学院学报，2009，23（1）：80-84+96.

[8] 王忆锋，唐利斌.利用有限差分和MATLAB矩阵运算直接求解二维泊松方程 [J].红外技术，2010，32（4）：213-216+230.

[9] 廖臣，祝大军，刘盛纲.五点差分格式求解泊松方程并行算法的研究 [J].电子科技大学学报，2008（1）：81-83+127.

[10] MAGRAB E B，AZARM S，BALACHANDRAN B.MATLAB原理与工程应用 [M].高会生，李新叶，胡智奇，等译.北京：电子工业出版社，2002.

作者简介：陈庚（2000—），男，满族，河北承德人，本科在读，研究方向：计算流体力学。

收稿日期：2023-03-20

基金项目：宁夏回族自治区大学生创新训练项目（S202211407040）