流域精细化水资源优化配置模型及应用
2023-02-28谭安琪穆振宇艾学山陈森林李天庆
谭安琪,穆振宇,艾学山,陈森林,李天庆
(1.武汉大学水利水电学院,湖北 武汉 430072;2.中国电建集团昆明勘测设计研究院有限公司,云南 昆明 650000)
0 引 言
我国水资源地区分布不均,水资源安全保障相较其他国家更具复杂性、长期性、严峻性和紧迫性[1-3],高效利用和配置有限的水资源,对于协调区域各用水部门之间的利益冲突[4],整体调控自然与社会诸因素[5],实现水资源的可持续利用和保障社会经济、资源、生态环境的协调发展具有十分重要的意义[6,7],而精细化水资源优化配置摆脱传统水资源优化配置结果模糊、配置精细度低的特点,能够涵盖流域内各个子节点,结果更为经济适用,是水资源可持续利用的重要手段[8]。
然而,由于水资源系统内元素众多,节点间多种多样的相互作用关系使得系统具有高度的空间复杂性[9,10],且流域内的用水需求(如灌溉需水)和供水要素(河道径流、水库库容、湖容量等)都具有明显的时变特征,这两者增加了流域水资源管理的复杂性和难度[11],是建立精细化水资源优化配置模型亟待解决的难点。针对此难点,部分学者从系统角度出发,先后采用大系统理论[12]、复杂水资源系统概化[13]、复杂适应系统理论[14]等方式描述流域内节点间的复杂关系进行空间水资源优化配置,黄强等[15]进一步制定了塔里木河干流流域水资源分配的网络节点图使得系统概化更为具体,Du 等[16]基于水系连通性构建了一个拓扑数字水网络用以进行水资源配置,Zhu 等[17]采用二阶段规划模型,即在水资源配置过程中将长期决策放入第一阶段,短期决策放入第二阶段进行求解,进一步将空间水资源优化配置与时间水资源优化配置相结合。上述研究推动了精细化水资源优化配置模型的建立与应用,但是,在模型时空配置结合方面,上述模型往往仅考虑用水单元的需求而忽略了水库这一重要供水单元的蓄水期库容要求,并且在描述节点间复杂关系时将其简单概化为单一的输入和输出,没有考虑水库节点随时间推移的蒸发渗漏损失以及用水节点和供水节点间的退水关系,从而使得节点间的复杂联系描述不清晰、不全面,进而导致模型精度和适用性受到一定影响。
针对模型时空配置中水库蓄水要求、忽略水库蒸发渗漏损失以及用水节点和供水节点间退水关系两方面问题,本文提出一种新型流域水资源优化配置模型,首先将流域内供水单元、用水单元进行分类,并针对不同类型单元建立约束条件,同时结合目标函数组成优化配置模型并以线性规划进行求解,最后通过南盘江流域水资源配置的实际应用进行检验。
1 系统计算节点分类
水资源配置系统主要包括4类要素:①供水及水处理工程。如水库、水闸、中水回用工程等;②用水单元。包括多种类型的各用水户单元;③河流;④输水渠道∕管道等,可将用水单元各类型(城镇、工业、农村、农业等)用水作为用水节点,其他作为供水节点。
1.1 供水节点分类编号
供水节点按照水库节点、水闸节点、中水回用工程节点顺序接续编号,设水库个数为MSK,水库序号集合记为:
设水闸个数为MZHA,水闸序号集合记为:
设中水回用工程个数为MZSHY,工程序号集合记为:
设NGS表示供水节点个数,即:
则供水节点序号集合记为:
其中任一类节点序号所属类型判断式为:
对于水库或水闸,其出库(闸)流量涉及最小生态流量限制[18],设ΩST表示出流具有最小生态流量限制的水库(闸)序号集合。
1.2 用水节点分类编号
设用水单元个数为MYSDY,单元序号集合ΩYSDY记为:
任意单元的用水类型总数为NYSLX,用水类型序号集合ΩYSLX记为:
将任一用水单元的任一用水类型作为一个用水节点,则最多总用水节点数NYS(实际系统每个用水单元并不一定包含所有类型)为:
用水节点序号集合为ΩYS:
式中:第i(∈ΩYS)用水节点表示第1+[(i- 1)∕NYSLX](取整)用水单元、第mod(i,NYSLX)(余数)种用水。
1.3 节点拓扑关系
基于水资源系统复杂性特点,可将水库和河流系统等简化为各种节点,用表示引水渠道或河段的连线对节点进行连接,从而组成一个流域水资源的物理拓扑网络系统[19],水资源配置系统有三种拓扑关系或水流联系:
2 流域水资源优化配置模型及求解方法
以系统来看,流域水资源系统由相互联系、相互影响、相互作用的若干个水源、供水工程和用水户组成[20],基于此特点,一方面,水源、供水工程和用水户可概化为若干个供水单元和用水单元,另一方面可根据单元之间出入流关系建立约束条件。
2.1 目标函数
设水资源系统配置期总时段数为T,优化准则为缺水量最小,则相应目标函数为:
式中:ΔS*为配置期最小总缺水量,万 m3;为t时段所有供水节点向第i∈ΩYS用水节点总的供给流量,m3s;Di,t为t时段第i用水节点需水流量,m3s;ΔTt为t时段长,s。
2.2 约束条件
约束条件分为两类,一是工程水量平衡约束,二是决策变量上下限约束。
2.2.1 水量平衡约束
水量平衡关系是用于描述任一时段内节点入流量、出流量、蓄水变化量等物理量之间的数学关系,是水资源优化配置模型中的基本关系之一,由于不同单元的入流、出流等条件各不相同,应根据单元特点进行分类并分别建立水量平衡关系约束。
(1)水库和水闸入库流量。水库、水闸的入库流量为:
式中:为第i水库(闸)t时段的入库流量,m3s;为第i水库(闸)t时段上游的区间流量,m3s;为第i水库(闸)t时段上游第j(j∈)供水节点的出流流量,m3s;为第j用水节点t时段的退水流量,m3s。
如果给定第j用水节点的退水系数为αj,则退水流量=;如果考虑滞时,比如2 个时段滞时(分别为βj,1、βj,2),则相邻2个时段的退水流量分别为
(2)供水节点水量平衡约束。水库水量平衡约束由五部分构成,一是水库入流量,二是水库出流量,三是水库供水量,四是水库蓄水变化量,五是渗漏及蒸发损失量,水量平衡约束如下:
式中:Vi,t-1、Vi,t分别为第i水库t时段始、末兴利蓄水量,万 m3;为第i水库t时段的出库流量,m3s;为t时段第i水库供给第j用水节点的供水流量,m3s;、为第i水库t时段的渗漏损失、蒸发损失,m3s;βi、γi,t为第i水库的渗漏损失系数、蒸发损失系数,10-4s-1;Ai,t-1、Ai,t分别为第i水库t时段始、末水库水面面积,万 m2。
水闸水量平衡约束:不需考虑蓄水变化量以及渗漏及蒸发损失量,流向下游的出闸流量加供水流量应该等于入闸总流量:
中水回用工程水量平衡:流向下游河道的流量加供水流量应该等于用水流量乘以回收系数:
式中:λj为第j用水节点的中水回用比例。
(3)用水单元供需水量平衡约束。用水单元水量平衡约束为:
2.2.2 上下边界约束
(1)水库库容上下边界约束。水库库容上下边界约束为:
式中:为第i水库t时段最大兴利库容,万 m3。
(2)水库及水闸下泄流量上下边界约束。水库及水闸下泄流量上下边界约束为:
式中:为第i水库或水闸t时段的最小下泄流量,即生态流量,m3s;为第i水库t时段允许的最大下泄流量,m3s。
(3)管道流量上下限约束。单一管道供给流量上下限约束为:
式中:为第i供水节点供给第j用水节点的流量上限,m3s。
复合管道复合流量上下限约束为:
式中:ΩGDk第k复合管道包含的所有供水—用水节点序号集合;为第k复合管道的输水流量上限,m3s。
2.3 数学模型求解方法
式(11)~(20)所组成的优化数学模型属于典型的线性规划模型,可以利用相关商业软件进行求解,且能求得全局最优解。
3 实 例
3.1 实例概况
南盘江发源于云南省曲靖市乌蒙山,经贵州省兴义市至广西红水河,是珠江的组成部分之一,其上游用水可分为农业、城镇、工业三类,为满足用水需求,需从临近的黑滩河流域进行调水。黑滩河为牛栏江右岸一级支流,属金沙江流域牛栏江水系,河道全长35.8 km,其中黑滩河水库为流域内最大水库,水库总库容13 500 万m3,坝高52 m,输水工程全长约18.728 km,是主要供水节点之一,其蓄水对保障枯水年供水,减少供水破坏时间,降低破坏深度具有重要影响。根据节1划分规则,对应流域网络节点图以及各类用水、供水节点如图1所示。
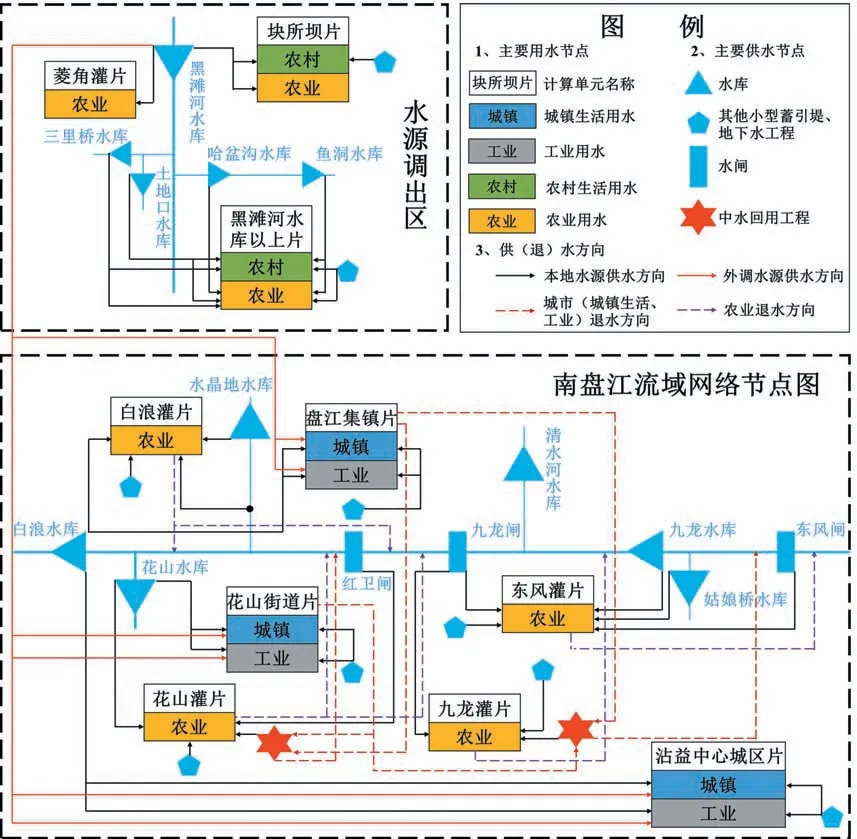
图1 南盘江流域及水源调出区网络节点图Fig.1 Network nodes diagram of Nanpanjiang River Basin and water source transfer out area
3.2 模型建立与求解
以缺水总量最小为目标,月为计算时段,选择水库(闸)年来水量、小水源供水量保证率为95%的年份进行水资源优化配置,由2.2 节方法分别建立水量平衡约束以及边界约束,采用线性规划方法进行求解,各供水节点、用水节点空间分配结果如表1所示。
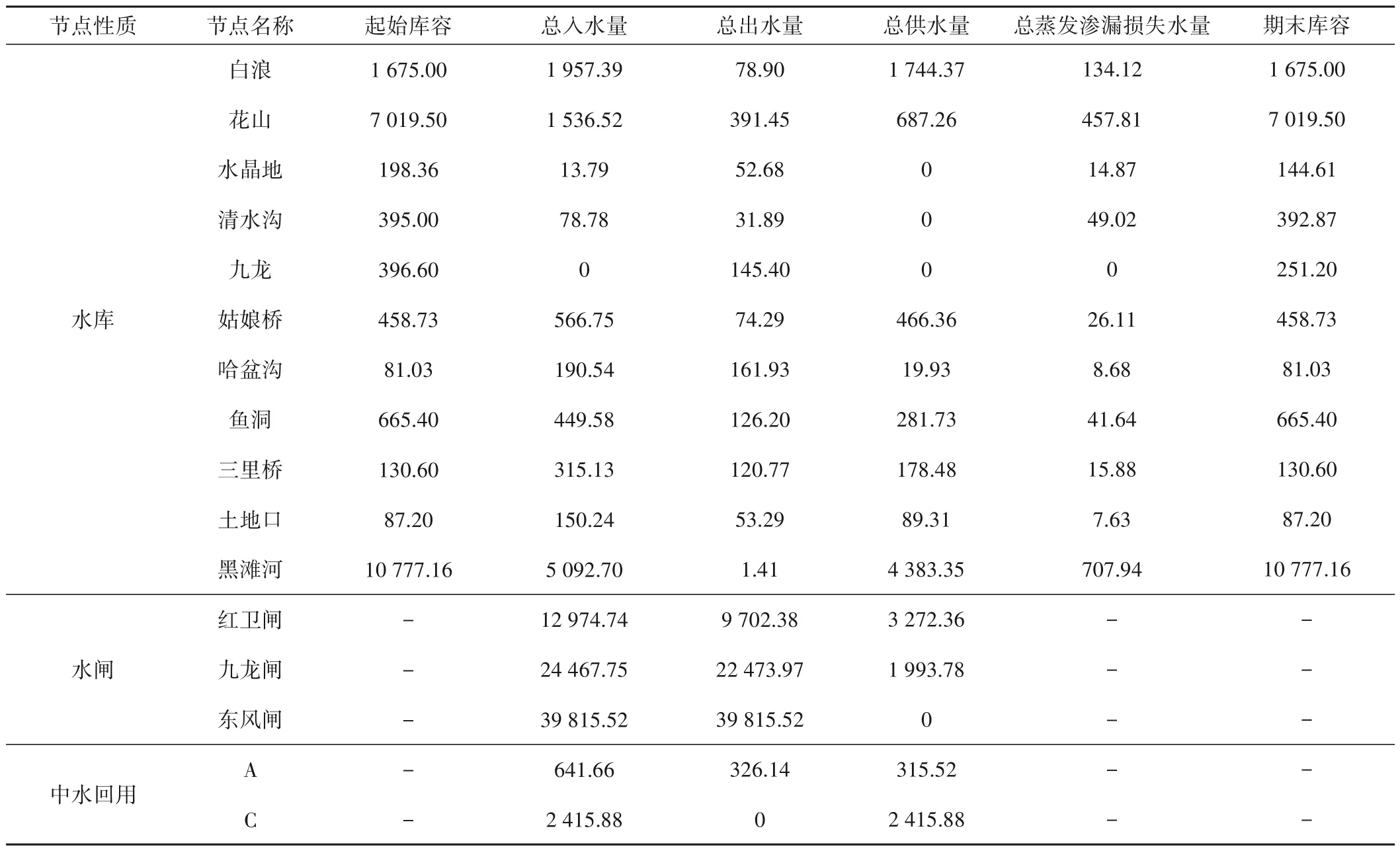
表1 供水节点各指标年统计结果万m3Tab.1 Annual statistical results of various indicators of water supply nodes
限于篇幅本文给出个别水库、水闸以及用水单元的水资源配置过程图,见图2。
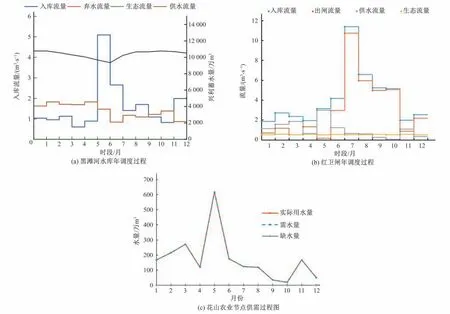
图2 水库、水闸以及用水单元水资源配置过程图Fig.2 Water resource allocation process of the reservoir,sluice and water use unit
3.3 成果分析
3.3.1 缺水分析
基于分类后的不同单元建立约束,采用线性规划针对总缺水量最小目标以及水库(闸)年来水量、小水源供水量保证率为95%的年份进行求解后,流域内农村用水、城镇用水满足率均为100%,农业用水满足率为97.7%,工业用水满足率为82.4%,基本实现了流域内的水资源空间配置,其中,工业缺水主要是由于管道输水限制,因此,为体现优化配置结果,本文进一步对缺水占比较多(17.9%)的黑滩河水库以上片农业用水节点进行缺水分析。

表2 用水节点各指标年统计结果万m3Tab.2 Annual statistical results of each index of water command node
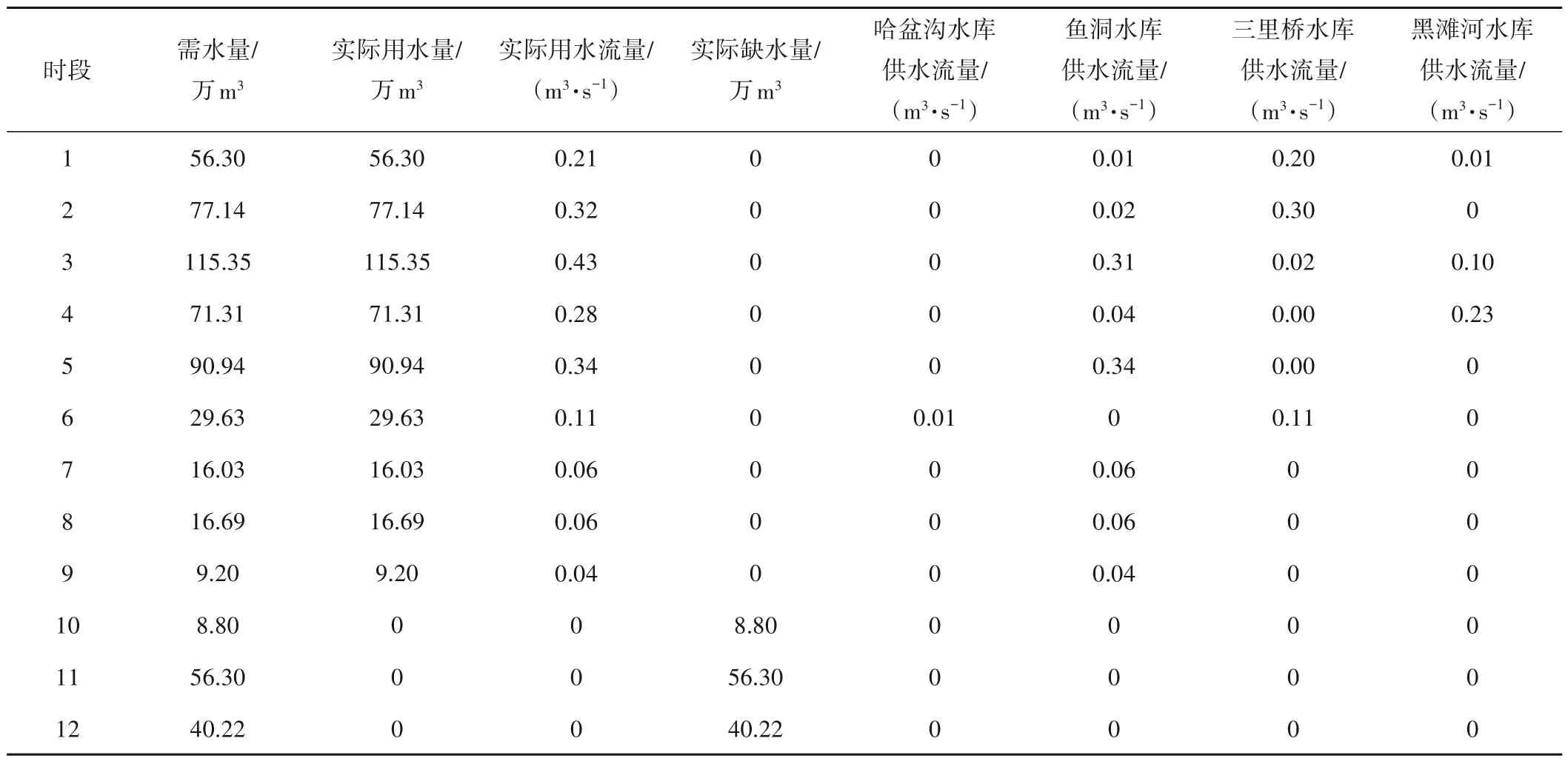
表3 黑滩河水库以上片农业用水节点年供水情况统计Tab.3 Statistics of annual water supply of the agricultural water node above Heitanhe reservoir
可见黑滩河水库以上片农业用水节点的缺水事件集中在10、11、12月,这是由于该时段为水库的蓄水期,为保证水库年末兴利库容满足要求,故哈盆沟、鱼洞、三里桥以及黑滩河水库不再向黑滩河水库以上片农业用水节点供水。
3.3.2 水库蓄水要求分析
在时间配置上,各水库均有效利用了不同时期的来水变化规律,除九龙水库外其余水库期末库容相较起始库容的变幅均不超过30%,其中流域内最大的黑滩河水库末时段库容与初时段相同,实现了有效蓄水,表4为黑滩河年调度过程。
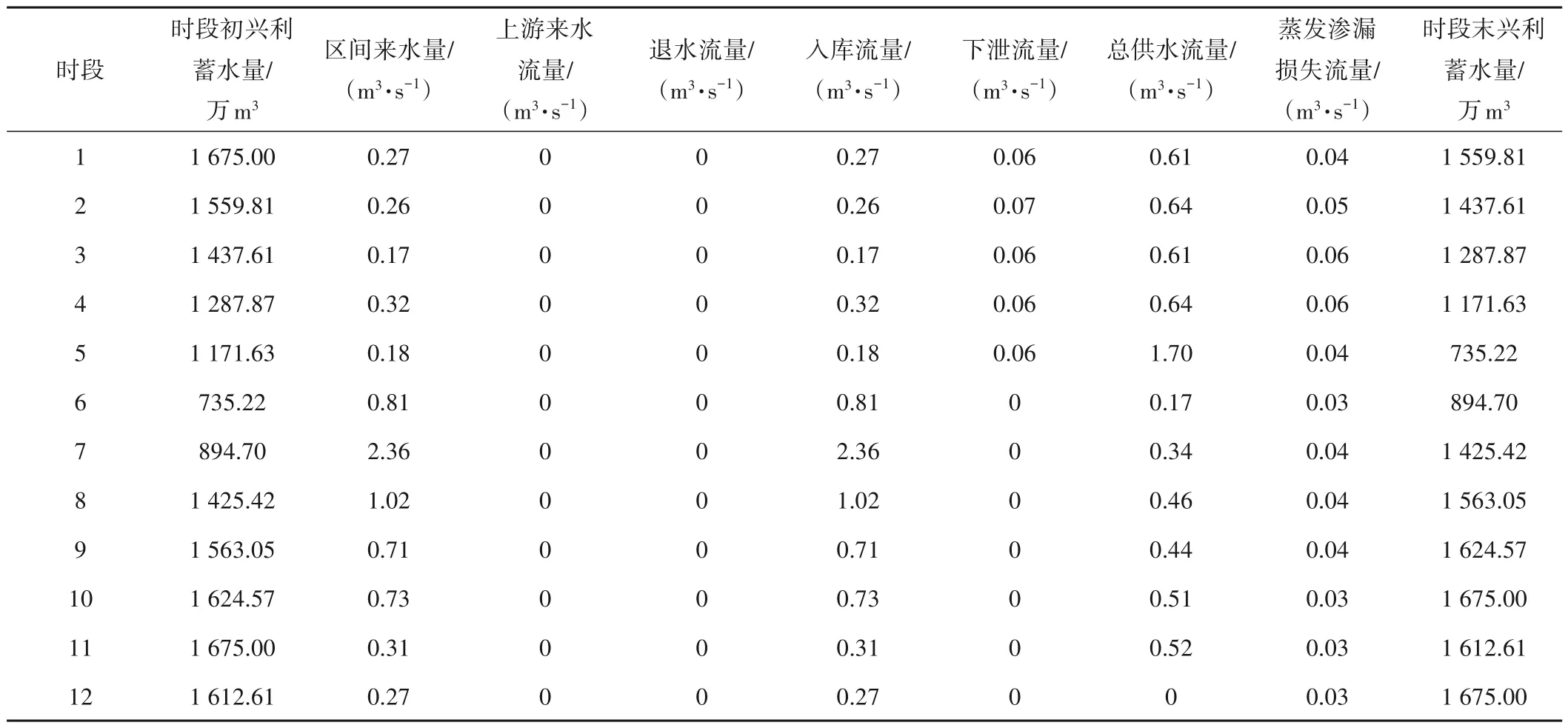
表4 黑滩河水库年调度过程统计Tab.4 Statistics of annual operation process of Heitanhe reservoir
3.3.3 蒸发渗漏损失以及退水分析
从表5可以得出,黑滩河水库总蒸发渗漏损失量占到了起始库容的6.6%,另一方面,白浪灌片农业用水中各月总退水流量在实际用水流量的占比达到了25%,可见水库蒸发水量、退水流量因素在水资源配置中具有不可忽视的影响。
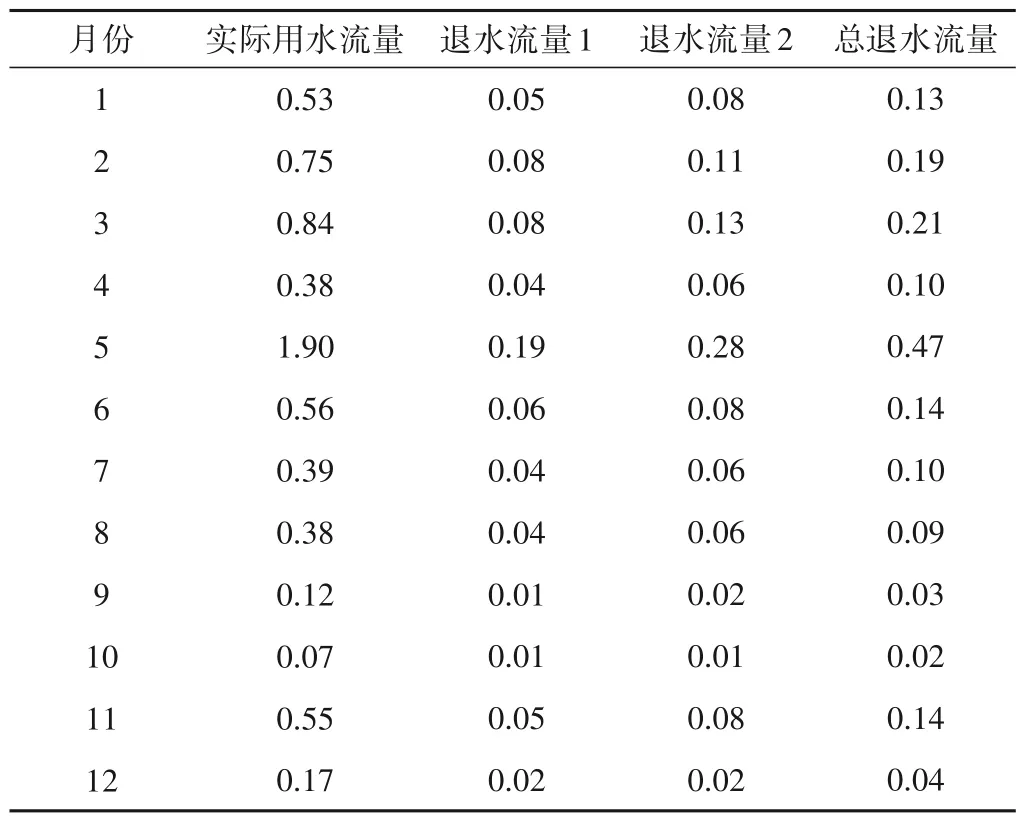
表5 白浪灌片各月实际用水流量与退水流量m3∕sTab.5 Actual water flow and backwater flow of Bailang irrigation in each month
4 结 论
为了精准描述水资源系统高度的空间复杂性和用水供水要素时变特征,本文首先将流域内供水单元、用水单元进行分类,并针对不同类型单元建立约束条件,同时结合目标函数组成优化配置模型并以线性规划进行求解,通过在南盘江流域的实际应用,可得出如下结论:
(1)本模型求解结果使得流域内农村、城镇用水满足率均为100%,考虑到年末水库蓄水要求以及管道限制,部分农业用水节点和工业用水节点存在缺水现象,总体上实现了时间空间双向尺度上的精细化配置。
(2)黑滩河水库总蒸发渗漏损失量占到了起始库容的6.6%,白浪灌片农业用水中各月总退水流量在实际用水流量的占比达到了25%,说明水库蒸发渗漏损失、退水流量等是水资源优化配置中不可忽略的因素。
(3)本模型精准描述了水资源系统内各节点间的复杂联系,可为复杂流域水资源配置的方案制定提供依据和指导。
