基于变折射率透镜原理的水波控制方法

王思莹，丁 宁 ，宋志伟 ，石小涛

(1.武汉理工大学 新材料力学理论与应用湖北省重点实验室，武汉 430070； 2.三峡大学 湖北省鱼类过坝技术国际科技合作基地，湖北 宜昌 443002)

1 研究背景

波浪蕴含的能量具有间歇性、随机性和波动性。巨型波浪可能给渔业捕捞、水上运输、涉水工程施工、海上国防军事活动等带来不利影响。常规波浪通过长期的拍击、剪切、液化和冲刷等作用也可能对海床、河堤、护岸等岸坡的稳定性产生破坏作用。除此之外，波浪对水中和沿岸水生生物造成的不利影响也不容小觑。研究表明，波浪的往复运动对岸坡植物产生的周期性拖曳力可能造成植株的物理破坏。同时，波浪的“泵送”作用可造成水底沉积物再悬浮，从而对水中生物群落造成一定影响[1-2]。传统工程通过修建防浪堤、种植防浪林等措施来保护岸坡，通过安装减摇装置来帮助船只或涉水平台对抗波浪的威胁。如果能直接规避波浪或者减弱波浪强度，势必可以大幅降低岸堤保护和涉水设施防浪的难度。

同时，波浪能也是一种无污染、储量大、分布广的可再生绿色能源。目前对波浪的利用集中于波浪能发电、挟带泥沙、引导排污等方面。其中海浪发电是波浪能的主要开发方式[3]。在波浪能开发中，可用波高出现的频率直接反映波浪能的可利用率。目前波浪能转化技术可利用的有效波高一般在1.3～4 m之间。波高过小不利于吸波，波高过大可能破坏能量转化装置。如果能够对波浪进行控制引导，将波浪高度控制在有效波高范围内，那对于收集波浪能来说会是个强大的助力。

可见，研究如何有效诱导水面波浪传播的路径、控制波浪强度的分布具有重要的科学意义和广阔的工程应用前景。考虑到水波的传播跟光、声、电、磁等波的传播控制方程存在相通的形式，近两年个别科学家开始探索变折射率透镜原理在水波传播过程中的运用。2014年，Kim[4-5]将Luneburg光学透镜聚焦光线的原理加以拓展应用，实现了通过改变流体密度聚焦声波的设计。2017年，Kim等[6]基于Eaton光学透镜回转光线的原理，提出了利用变密度橡胶柱墙体来改变海啸波传播方向，以及防范海啸危害的原理和方法。2019年，Zou等[7]基于梯度折射率超材料的电磁波隐形理论方法，提出并验证了通过布置特殊形状的水下障碍物来消减水面波浪的方法。 这些工作打开了利用流体域内密度、水深等参数的梯度变化来实现波浪控制的新局面。

变折射率透镜(Gradient Index Lens)是使用具有梯度折射率的介质设计和制造的光学成像元件。Luneburg[8-9]和Eaton[10]分别在1944年和1952年提出了2种不同的球对称变折射率透镜模型，其折射率分布为：

(1)

(2)

式中：n表示折射率，下标L、E和0分别表示Luneburg、Eaton透镜和参考背景中的数值；r为当前位置到球心的距离；R为透镜半径。理论分析和试验验证表明，当平行光从Luneburg透镜一侧射入，会在对侧边缘形成聚焦点，而通过Eaton透镜的光线将绕着透镜的中心以相反方向射出，即光线不会进入透镜后面区域(见图1)。

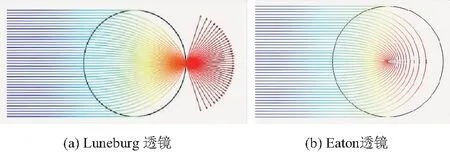
图1 光线穿过变折射率透镜的路径Fig.1 Trajectories of light passing through the Luneburg lens and the Eaton lens

至今，Luneburg透镜和Eaton透镜对光线、电磁波、声波等的控制理论和作用原理已经十分明确，在光、声、电、磁学等领域都有广泛而成熟的应用。如Luneburg透镜因其聚焦波与折射镜像放大的特性被广泛地用于雷达、光路、扬声器的设计中[11-13]。而Eaton透镜对波的偏转作用也被用来制作光隔离器、声偏转器、声学斗篷等[14-15]。

本文拟基于Luneburg透镜和Eaton透镜的折射率分布函数，推导可让水面波聚焦和回转的变密度流体区域的密度分布函数，并通过数值模拟对设计出的特殊变密度流体域对水波的控制效果进行验证分析。

2 理论分析

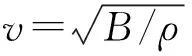
(3)

式中v0和ρ0分别为背景流体中的波速和流体密度。依据Luneburg透镜和Eaton透镜的折射率分布函数式(1)、式(2)，可以推算出对水波具有类似控导功能的流体域密度分布满足以下形式：

ρL(r)=ρ0[2-(r/R)2] ，

(4)

ρE(r)=ρ0(2R/r-1) 。

(5)

式中ρL和ρE分别表示根据Luneburg透镜和Eaton透镜设计的“变密度水波透镜”的流体密度分布函数。

从上述公式和图2可以看出，依据2种透镜设计的变密度水波透镜内各处的流体密度均大于背景材质水的密度，且越靠近圆心区域，流体密度越大。Luneburg水波透镜圆心位置的流体密度为水密度的2倍。Eaton水波透镜中心区域的流体密度极大，圆心位置的密度理论计算值为无穷大。实际应用时，可放弃中心区域，采用环形流体域发挥作用。

图2 水波透镜的流体密度空间分布Fig.2 Spatial distribution of fluid density in water wave lenses

按照变折射率透镜对光线的作用效果可以推测，波浪经过Luneburg水波透镜之后会聚焦于该区域边缘一点，使得该点的波浪强度明显增大；而经过Eaton水波透镜之后，波浪的传播方向会发生180°的偏转，即波浪转为向上游传播，变密度流体区域的下游可免受波浪影响。流体密度的改变，可以通过在水域中排布不同直径和密度的橡胶柱或者气囊阵列来实现。对于具体设计和实现过程，前人在进行声波透镜的研究过程中有所尝试，并获得了预期效果[4-6]。本文由于试验条件限制，目前尚未开展相关工作，而选择用数值模拟分析来验证波浪在各种变密度流体区域影响下的传播效果。

3 计算方法

水面波浪传播的控制方程可以用无黏不可压缩流体的动量守恒方程来描述，也就是Navier-Stokes方程，即

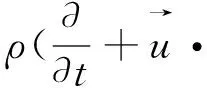
(6)

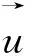
(∇2+k2)φ=0 。

(7)

式中k是波数。本文选用Comsol Multiphases软件中的压力声学模块来对该方程式进行求解分析。大量研究工作已经表明，该模块可实现包括声波、应力波、水波等各种波在介质中的传播过程的模拟分析。

本文采用的计算模型如图3所示。单个水波透镜的计算域大小为2 m×2 m，多个透镜组合的计算域根据具体情况选定。均匀密度区的材料为水，流体密度、声速、体积模量、阻抗等参数根据选取的材料自动赋值。中心半径R=0.3 m的圆形区域为变密度流体区域，该区域的流体密度按密度分布函数式(4)和式(5)来设置，其余材料参数不变。以压力幅值P0=1 Pa 的平面辐射波作为入射压力场条件。为观测波浪传播效果，分别对平行波从半区域(图3(a))和全区域(图3(b))入射两种情况进行研究。其中半区域入射的模型通过在透镜上游中心线上布置内部声学硬边界条件(墙)，将模拟区域划分为上下两部分，由于墙体的存在，波浪仅能通过透镜后影响到上侧区域。2个计算模型中除波浪入射边界之外的边界均设置为阻抗边界。

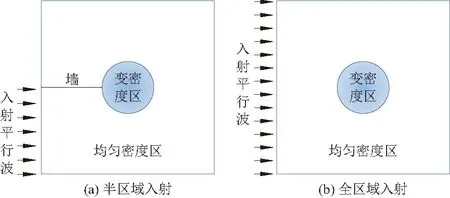
图3 计算模型Fig.3 Numerical models

4 结果分析

4.1 波浪传播路径

为观测变密度流体域对波浪传播方向的偏转作用，本文将图3(a)所示模型的中心圆形区域分别设置为均质水、混疑土、Luneburg变密度流体和Eaton变密度流体4种参数情况，模拟了频率f=25 Hz、压力幅值P0=1 Pa的平行入射水波在这些物质影响下的传播效果。

从图4展示的水面压力P分布云图可见，4种情况下波浪的传播路径有很大区别。如图4(a)所示：全场均匀材料的水域中，平行入射的波浪呈现无阻碍向下游传播的趋势；在圆形区域下游，有波浪入射的下半部分水域存在与入射波强度相当的波浪，而没有波浪入射的上半部分水域的波浪强度则很弱。而如图4(b)所示：在水域中放入一根混凝土柱时，波浪受其阻碍作用，绕过柱体向下游传播；相应地混凝土柱下游的波浪极不明显。当圆形区域内是Luneburg变密度流体时，平行波流经该区域后聚焦于变密度区域外边缘处，并向下游继续发散传播(图4(c))。当圆形区域内是Eaton变密度流体时，平行波流经该区域后传播方向回转，转为向上游方向传播，在下游不会出现明显的压力幅值(图4(d))。

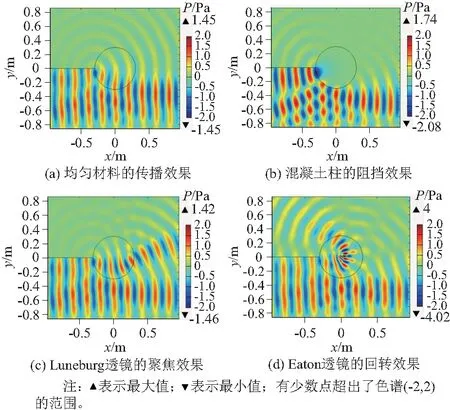
图4 不同流体材料影响下的波浪传播Fig.4 Wave propagations under the influences of different fluid materials

4.2 波浪强度分布

为了进一步观察不同变密度流体区域对水面波浪的作用效果，本文基于图3(b)所示的全区域入射波模型，对不同布置方案下，频率f=25～75 Hz的水波在2种变密度流体透镜作用下的强度变化进行了数值模拟。

图5给出了平行入射水波在Luneburg变密度水波透镜影响下的压力分布。可以看出平行波的传播方向在变密度流体区域发生了偏转，并聚焦在透镜下游边缘(0.3 m，0 m)处，之后以该点为中心发散传播。整个计算域的最大压力总是发生在该聚焦点处，该点的压力幅值数值明显大于入射波的初始幅值1 Pa。从图5还可以看到，入射波经过Luneburg透镜之后，由于波的叠加作用，在聚焦点后方两侧间隔地存在一定范围的压力减弱和增强区，区域的位置和大小随入射波频率的变化而有所不同。

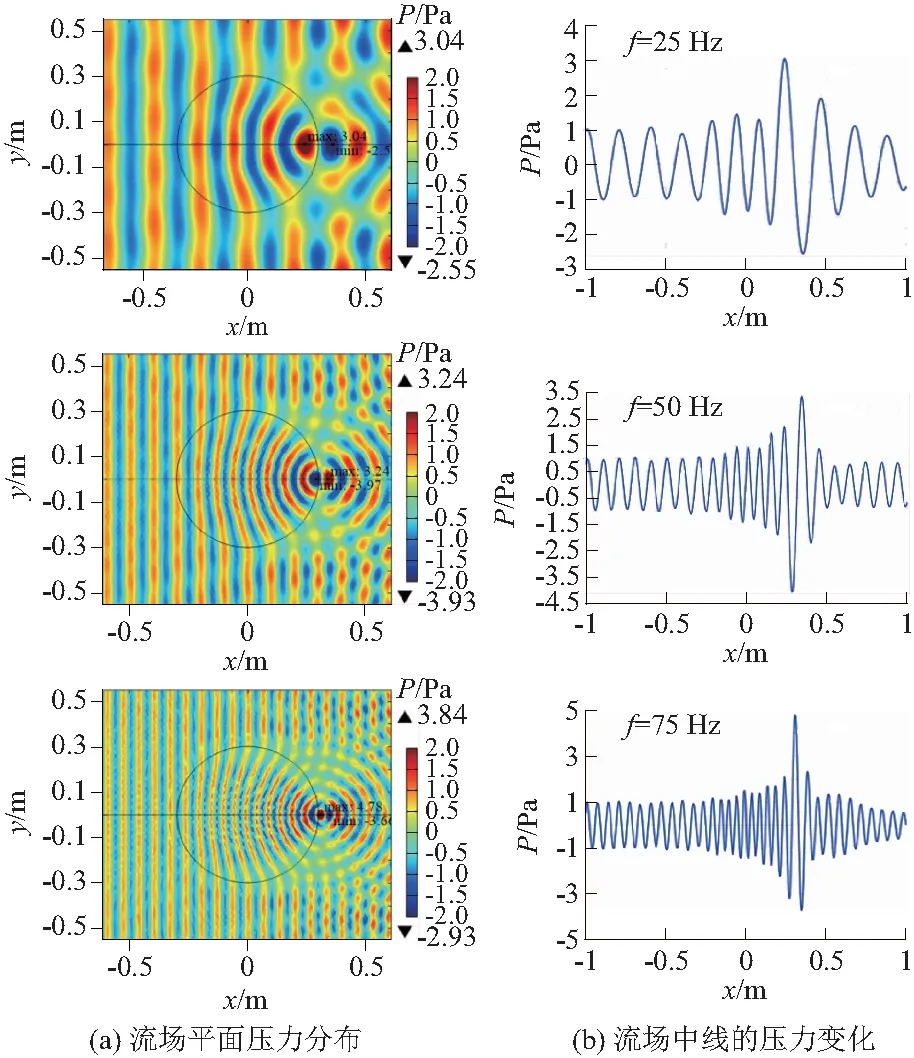
图5 水波穿过Luneburg变密度流体域的压力分布Fig.5 Pressure distribution of water wave passing through Luneburg lens

如图6所示，Eaton水波透镜对不同频率的入射波都会产生回转的效果，尤其对频率较高的波浪作用更为明显。从压力云图可以看出，波浪从左侧边界平行入射，经过Eaton变密度流体区域时，原本平行向右的传播方向发生回转，变为向左传播。由于入射波和反射波的叠加，变密度流体区域及其上游的压力幅值增大。整个计算域压力绝对值的最大值总是位于透镜中心处。变密度流体区域下游的压力幅值明显低于入射波的初始幅值，证明Eaton水波透镜确实可以消减下游区域波浪的强度。从整个水域中线上的压力分布曲线可以看出，通过变流体密度Eaton透镜后，水波的压力幅值减小至输入波压力幅值的一半左右，这也与Kim等[6]研究Eaton声学透镜得到的效果基本吻合。

图6 水波穿过Eaton变密度流体域的压力分布Fig.6 Pressure distribution of water wave passing through Eaton lens

理论上说，不同频率的波浪经过透镜的作用效果应该保持规律一致。对更宽频率范围的入射波传播效果的数值模拟结果表明，对于频率很低的波浪，由于其波长较长，与透镜尺寸相当或者更大，从图像中看不出传播方向的变化。对于频率较高、波长较短的波浪，如图6所示，都能较明显地看出变密度流体域影响下波浪传播路径的偏转和强度分布的变化。对于频率更高、波长更小的波浪，均能看出类似的趋势，但所形成的条纹更为密集，分辨度不高，因此本文未做更多展示。现实中的水面波浪受水深、风速、风向与地形等条件的影响，波长范围可以从几厘米至几百千米。为将透镜原理有效地应用于波浪的控制和引导，可以以水域的常见波浪波长为依据设定变流体密度区域的尺寸，保证透镜作用区域的范围大于几倍波长，即可发挥变密度流体对波浪的聚焦和回转作用，从而增强波浪强度以收集利用或者消减强度来实现对下游区域的保护。

4.3 多个透镜组合运用

基于单个透镜对波浪的作用，本文也尝试对多个变密度流体区域组合影响下的波浪传播进行了分析。所用的计算模型和参数设置与图3(b)类似，每一个透镜的大小仍然取半径0.3 m。只是根据透镜数量和排布位置改变了变密度流体域的范围，并根据需要适当增加了计算区域的大小。

图7给出了多个变密度流体域在几种典型排列模式下对平行入射波传播的影响效果。可以看出，多个水波透镜在流场中共同作用时，效果相当于多个透镜单独作用效果的叠加。当2个或3个Eaton水波透镜并行排列时，可以使通过变密度流体域的波浪压力幅值降低为输入时的1/2左右。5个Eaton水波透镜呈双列交错排布模式时，其输出波的压力幅值为输入值的1/4左右。Luneburg水波透镜对波浪的聚焦再发散传播的影响也与理论预期基本一致。聚焦再发散形成的多列波浪相互作用之后，透镜下游的波浪强度呈现增强、减弱区交错分布的情况。 在5个交错排布的Luneburg透镜作用下，入射平行波经过第一列透镜聚焦后再发散，又因为第二列透镜再次聚焦，整个计算域的压力最大值出现于第二次波聚焦点，也就是第二列透镜的下游边缘处。

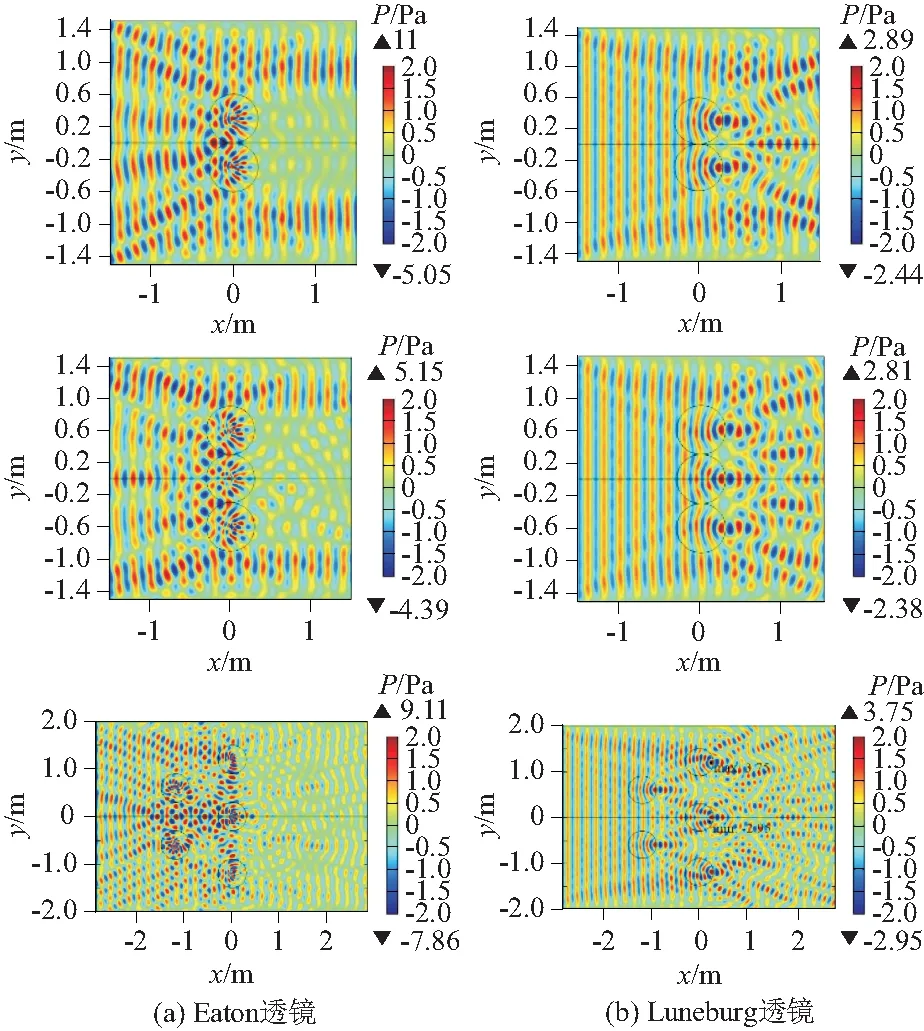
图7 多个水波透镜组合作用的效果Fig.7 Combined effect of multiple water wave lenses

可见，在水域中布置多个变密度水波透镜来实现对水面波的调控是可行的。根据具体工程的应用需求和现场条件，设计布置不同大小和功能的变密度流体区域，可以得到各式各样的波浪调配结果，这为水利和海洋工程中制定波浪的防范和利用措施提供了一个新的思路。

5 结 论

本文通过理论推导和数值模拟验证，针对Luneburg和Eaton这两种不同功能的变折射率光学透镜在水面波浪传播控导中的应用技术进行了研究。根据这两种透镜的折射率分布函数推导出了具有类似功能的变密度流体区域的密度分布公式，并通过数值模拟分析了不同类型的变流体密度水波透镜对平行入射波浪的作用效果。主要结论有：

(1)依据Luneburg透镜设计的变流体密度水波透镜可以让平行入射的水面波聚焦于一点，使得该点的波浪强度显著增强，利于收集利用。

(2)依据Eaton透镜设计的变流体密度水波透镜可以让平行入射的水面波转向传播，使得该透镜区域下游的波浪强度减弱为入射波强度的一半左右，从而消减该区域内受到的波浪影响。

(3)多个变密度水波透镜组合应用，对波浪的控制效果为单独作用时的效果叠加。

本文研究工作提供了利用变参数流体域来控导波浪传播路径的方法和效果仿真验证，为防波减浪措施的制定和波浪能收集利用提供了一个新思路。考虑到改变流体密度在实际应用方面存在一定局限性，在后续工作中我们将针对变水深的水波控导理论开展进一步工作，以期实现通过设置水下结构，构建特殊水深分布形态，从而对水面波浪加以控导利用。