基于改进PSO算法的导叶式旋风分离器结构参数多目标优化

2023-02-28梁海琴施炜炜张鑫睿于丰瑞

机床与液压 2023年3期

梁海琴，施炜炜，张鑫睿，于丰瑞

(新乡航空工业(集团)有限公司上海分公司，上海 201201)

0 前言

旋风分离器是环控系统中的重要基础元件，其作用是分离气流中的固体颗粒杂质。旋风分离器的应用迄今已有百年历史，在多行业的过滤系统中得到广泛应用[1-2]。为了提高旋风分离器的性能，众多学者对旋风分离器的结构设计以及参数优化进行了研究。文献[3]研究了不同导叶结构对旋风管分离性能的影响，指出随着叶片数量或叶片厚度的增加，其分离效率和压降也逐渐增大。文献[4]提出一种新型分流式旋风分离器内部结构并对其进行研究，结果表明这种新结构有效降低湍流强度。文献[5]选取4个关键设计变量，通过对旋风分离器的结构参数进行优化以提升分离效率。文献[6]利用响应面法对多参数进行优化组合以减小压降。文献[7]研究了旋流偏心率对分离器性能的影响，结果表明偏心率越大，压降也越大。上述研究多采用控制变量法进行单因素优化，其性能提升有限，或采用局部多因素组合优化，其前处理复杂且计算量大导致耗时较长，主要原因为旋风分离器各几何参数之间互相制约。

针对上述研究中存在的不足，本文作者提出基于旋风分离器结构参数化模型的综合优化方法。采用脚本建模方法构建旋风分离器参数化模型，通过CFD计算与试验进行对比分析，对参数化模型准确性进行验证。结合拉丁超立方抽样法选取全局高灵敏参数，利用改进PSO算法以分离效率和压降为性能目标进行优化，旨在进一步提高旋风分离器性能。

1 数值模拟准确性验证

1.1 工作原理及建模过程

某导叶式旋风分离器主要由导流叶片、壳体及管接头组成，如图1所示，气体与颗粒物杂质从进口入，通过离心力将颗粒物甩向壁面，杂质或与壁面碰撞反弹或被壁面粘附，大量杂质由于重力作用会沿着壁面从集尘口排出。

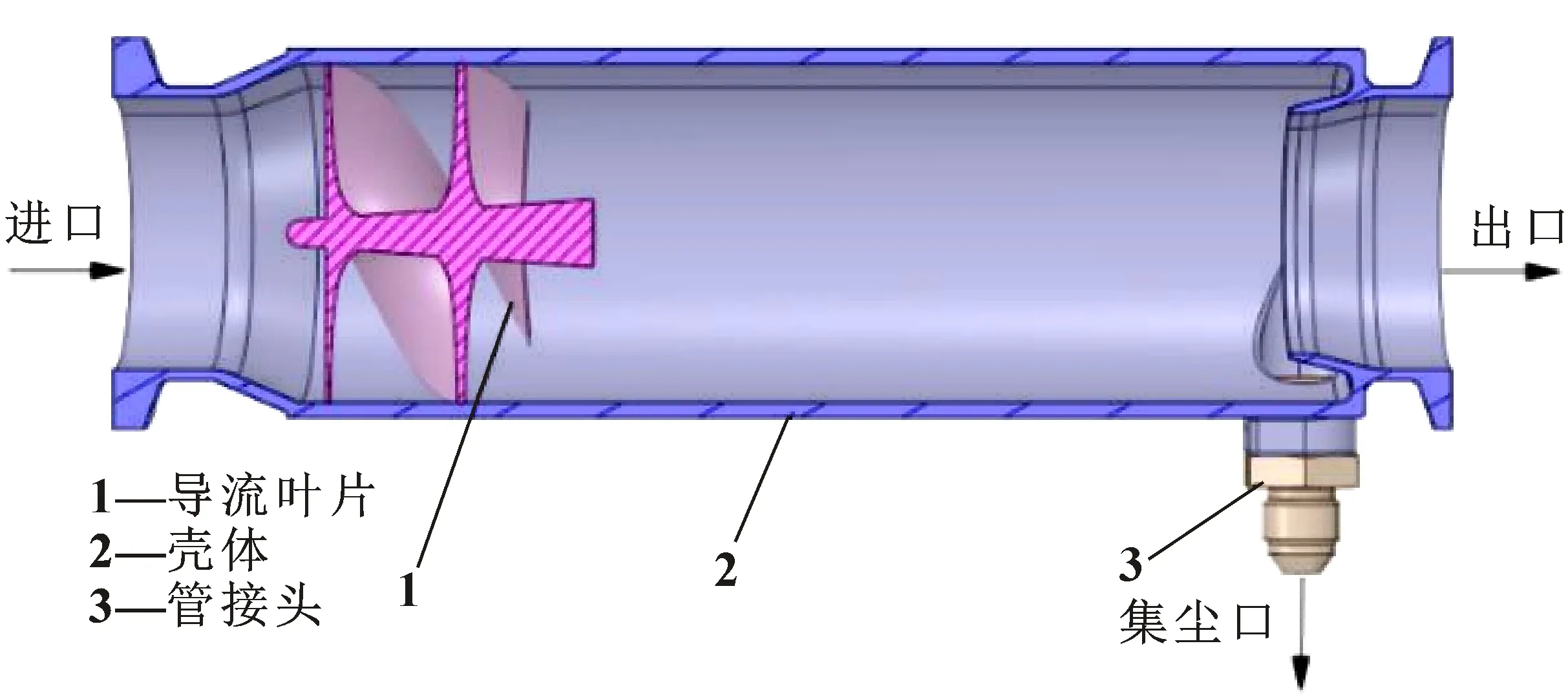
图1 导叶式旋风分离器结构与原理Fig.1 Structure and principle of guide vane separator

通过SCDM软件脚本建模模块，构建导叶式旋风分离器的参数化初始模型。关联到14个设计参数，参数标注如图2所示，初始结构参数见表1。脚本建模模块可快速实现产品参数化建模，通过改变几何参数来驱动脚本改变几何模型。该方法无需在三维软件中重新手动构造几何模型，可直接获得改变参数后的几何模型，使得设计效率更为高效，可大幅缩短仿真前处理周期，从而提升仿真计算效率。

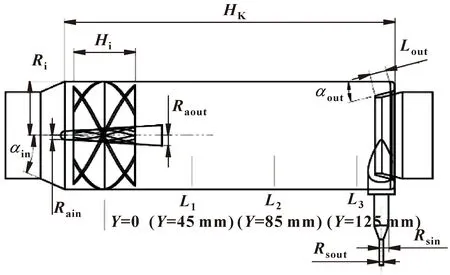
图2 参数标注示意Fig.2 Parameter annotation

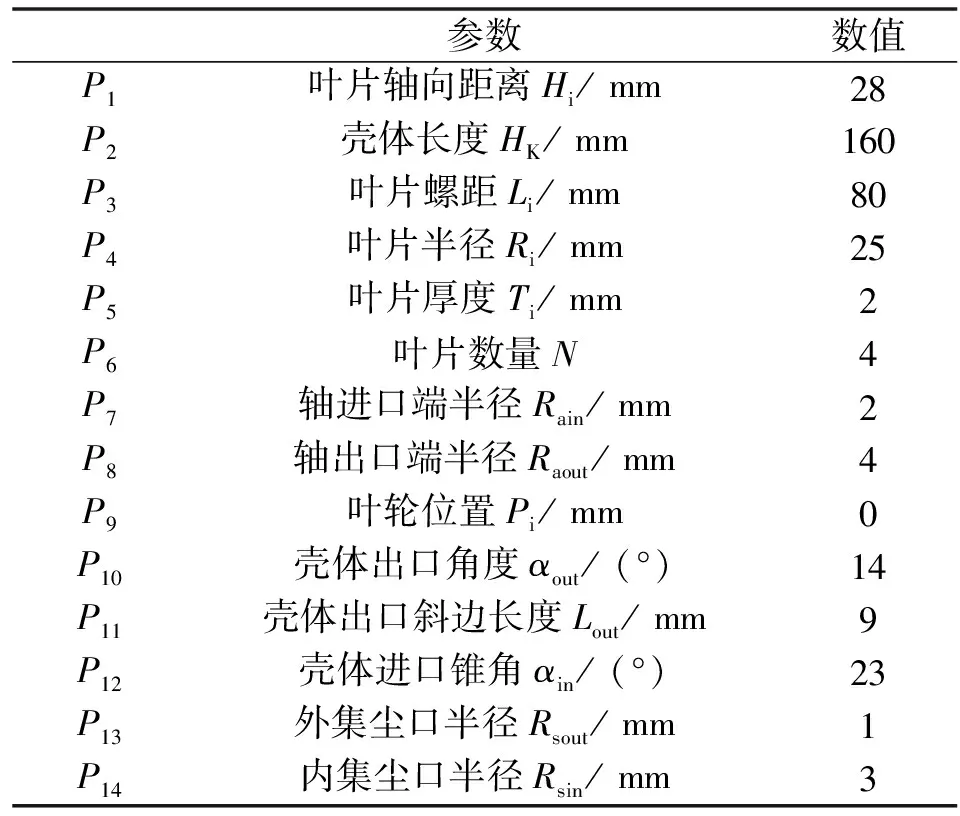
表1 初始结构参数Tab.1 Initial structure parameters

1.2 压降与分离效率试验

将产品连入试验台，如图3所示。试验原理如图4所示，顺箭头方向通入空气，在入口空气温度340 ℃, 入口压力558 kPa，空气流量分别为650、700、750、800 kg/h时，实测旋风分离器进、出口压差。在空气流量为800 kg/h时，通过加尘系统开始添加粉尘(铝粉)并保持10 min，粉尘添加量130 g/min，实测并记录添加粉尘质量ms和集尘箱的质量增量ΔmB。分离效率η计算公式如下：

η=ΔmB/ms

(1)

所采用的铝粉粒径分布由马尔文激光粒度仪测量，如图5所示。用比重瓶测其颗粒密度为2 719 kg/m3。

图3 试验台Fig.3 Test-bed

图4 试验原理Fig.4 Test principle

图5 铝粉粒径分布Fig.5 Distribution of aluminum powder particle size

1.3 数学模型及颗粒相边界条件

目前对导叶式旋风分离器模拟分析的研究成果[8-10]中，雷诺应力模型(RSM)的计算结果与试验结果最相近，该湍流模型的可靠性较高，因此采用RSM湍流模型进行计算。

计算颗粒选用原模型试验用标准铝粉作为模拟计算的对象，计算中不考虑颗粒质量变化与热量传递。假定所用铝粉粒径满足Rosin-Rammler(罗辛拉姆特分布)，并用图5数据回归可得如下指数关系：

(2)

1.4 准确性验证

采用非结构网格。为验证网格无关性，以分离效率为网格无关性验证依据，在不同划分水平下网格单元数分别为168万、253万、345万、457万、550万。计算结果表明：当网格数量大于253万时，网格数量对计算结果的影响可以忽略。因此选用网格数为253万的网格划分方案进行后续的模拟计算。压降试验结果与模拟结果对比如图6所示，其中，试验数据为多次测量并剔除异常值后取的平均值，分离效率试验结果为85.1%。从图6中可知：压降试验数据与模拟数据误差较小，表明数值模拟准确性较高。

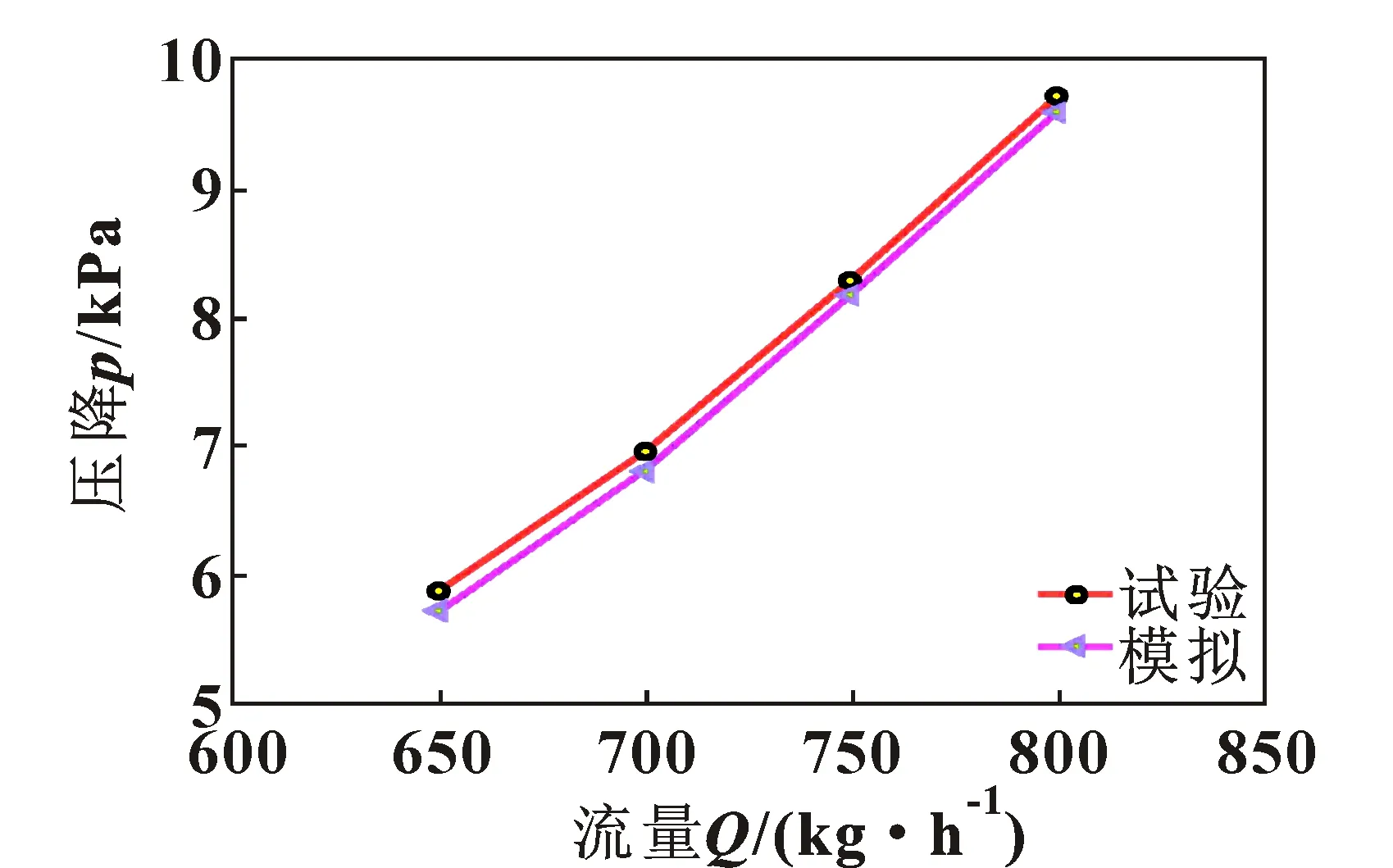
图6 原模型压降模拟值与试验值对比

以分离效率的试验数据为对标标准，通过修正颗粒与壁面的碰撞系数，使原模型分离效率的模拟结果与试验结果对标误差在3%以内。采用命令批处理的方法，通过迭代修正壁面碰撞系数以满足对标误差要求，计算得到壁面反弹系数为0.95，其性能结果的模拟值与试验值如表2所示。将标定的壁面反弹系数0.95作为参数化模型计算的一个重要边界条件。

表2 原模型性能的模拟值与试验值

2 参数优化

由于导叶式旋风分离器关联的设计参数较多，因此需要确定目标函数对各相关设计参数的灵敏度，样本空间由拉丁超立方抽样法完成，并基于高灵敏度设计参数利用改进的PSO算法进行全局寻优。

2.1 灵敏度分析

目标函数Y与设计参数向量X之间满足[11]：

Y=y(X)

(3)

X=(X1,…,Xi,…,Xj,…,Xn)T

i,j∈(1,2,…,n)

(4)

式中：n为设计参数的个数。

将设计参数Xi与Xj之间的相关系数记为ρij，当i=j时，ρij=1；当i≠j时，在设计参数的方差和协方差矩阵Var(X)中，相关系数个数为n(n-1)/2。

由

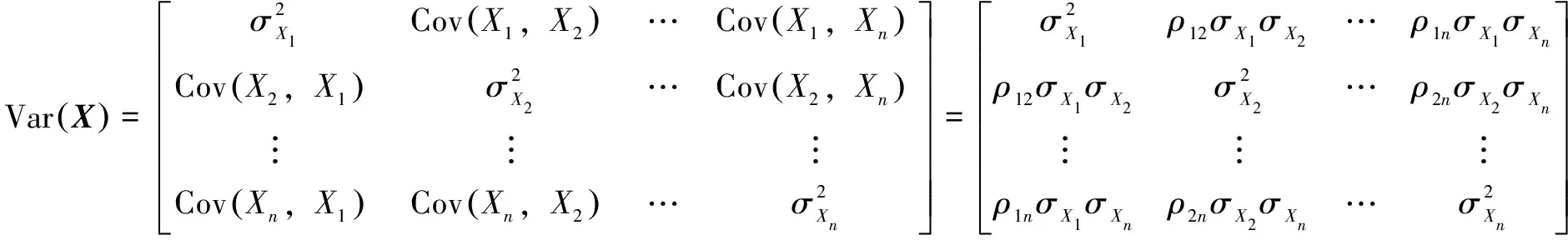
(5)

及

(6)

(7)

可得

(8)

由

(9)

可知：σY为ρij的函数，即σY=f(ρij)。

而目标函数Y的指标α可表示为

(10)

目标函数对设计参数间相关系数的灵敏度表达式为

(11)

拉丁超立方抽样法是改进的蒙特卡洛法[12]，样本效率比蒙特卡洛法提高约12倍，能够最大限度减小样本相关性并避免样本聚集，保证每个样本的有效性。两种方法的样本分布如图7所示。

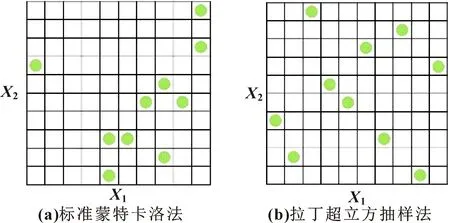
图7 样本分布策略

通过拉丁超立方抽样法完成样本空间，模拟样本数为500，共14个设计参数变量，目标函数分别为分离效率与压降。通过计算获得14个设计参数对某导叶式旋风分离器分离效率和压降的灵敏度水平分别如图8、图9所示。

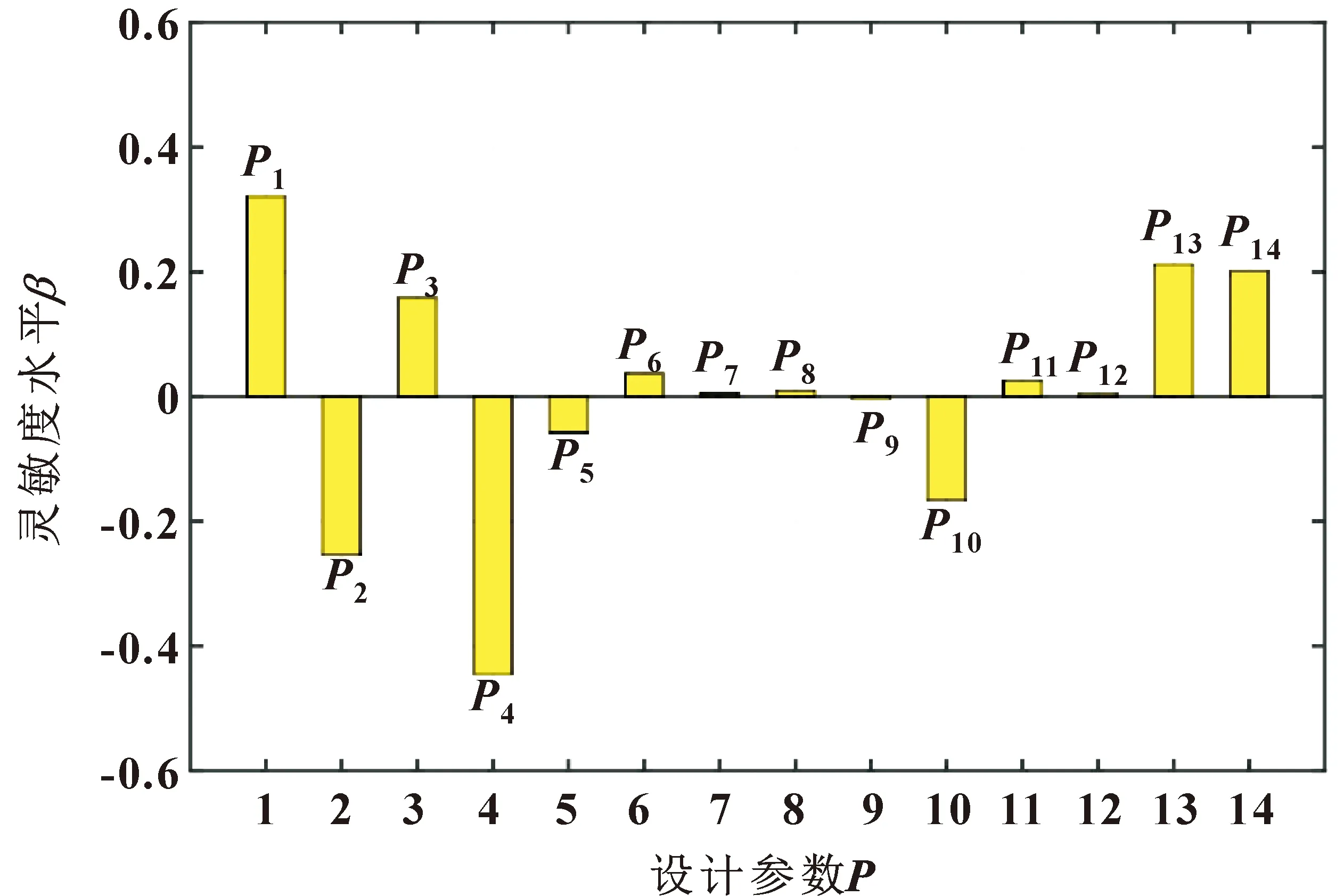
图8 分离效率对设计参数的灵敏度

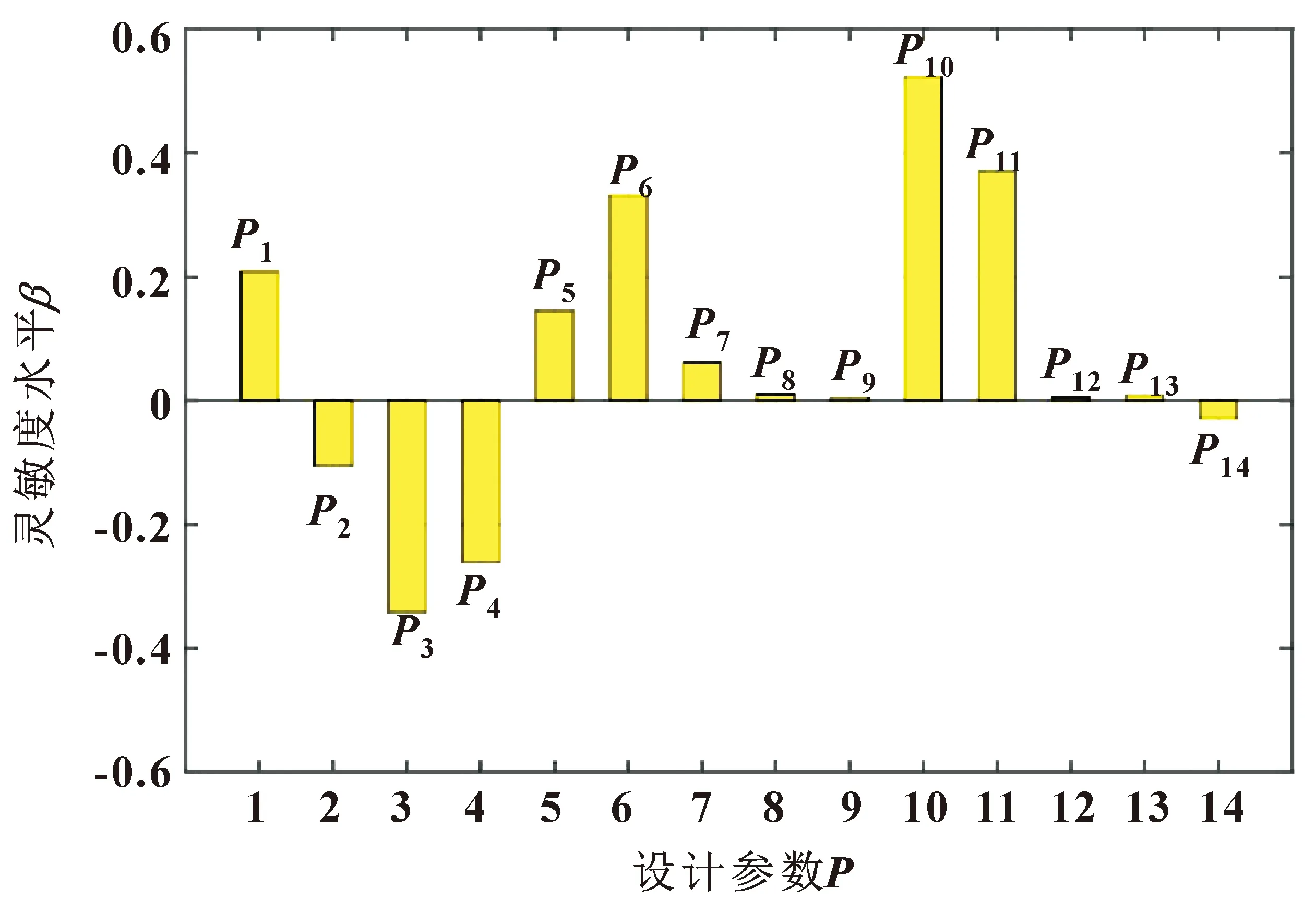
图9 压降对设计参数的灵敏度Fig.9 Sensitivity of pressure drop on design parameters

从图8可以看出：叶片轴向距离Hi、壳体长度HK、叶片半径Ri对分离效率均表现出了高灵敏度水平；其中叶片半径Ri对分离效率的影响最大，且为负相关。

从图9可以看出：叶片螺距Li、叶片数量N、壳体出口角度αout和壳体出口斜边长度Lout对压降均表现出了高灵敏度水平；其中壳体出口角度αout对压降的影响最大，且为正相关。综合灵敏度分析结果可知，共7个结构设计参数体现了高灵敏度水平。

2.2 基于改进PSO算法寻优

粒子群算法(PSO)特点在于搜索过程跟随当前最优解并将最优解信息传递给其他解，单向传递，收敛速度更快。而遗传算法(GA)种群个体信息共享，整个种群向最优区域均匀移动，具有强大全局搜索能力。因此PSO算法结合GA算法交叉能力后改进的算法[13]，不仅可以全局寻优，并加快收敛速度。本文作者基于MATLAB完成改进的PSO算法程序，通过对PSO算法惯性权重及学习因子[14]编码，编写粒子交叉能力程序，并将种群随机初始化编码改写为种群设定初始化。

采用改进的PSO算法对参数化模型进行寻优，选取与分离效率和压降相关的7个高灵敏度水平的设计参数为优化变量，其约束条件如表3所示。以分离效率与压降为优化目标，其优化模型为

(12)

式中：η为分离效率；p为压降。

表3 设计参数约束条件Tab.3 Design parameters constraints

以灵敏度分析得到的最优解为初始种群个体，设定初始种群个体数1，最小遗传代数5，最大遗传代数20。

基于改进PSO算法寻优得到参数化模型带Pareto前沿的优化解集如图10所示，从Pareto前沿[15-16]中找到合适的优化方案A与优化方案B。原模型与优化后模型模拟值对比如表4所示，相比于原模型，方案A的分离效率提升了12.41%，压降降低约1.7 kPa；方案B的分离效率提升了10.31%，压降降低约3 kPa。

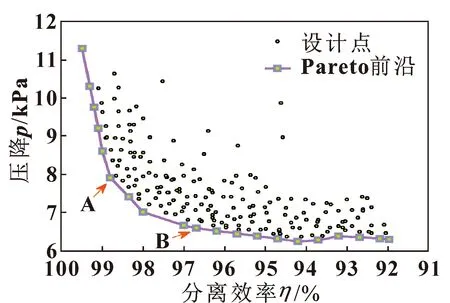
图10 参数化模型的优化解集Fig.10 Optimized solution set of parametric model

表4 原模型与优化后模型模拟值对比

3 优化前后对比分析

3.1 优化后模型参数

优化后两种方案模型参数的取值及变化率分别如表5和表6所示，负号表示该参数负增长。

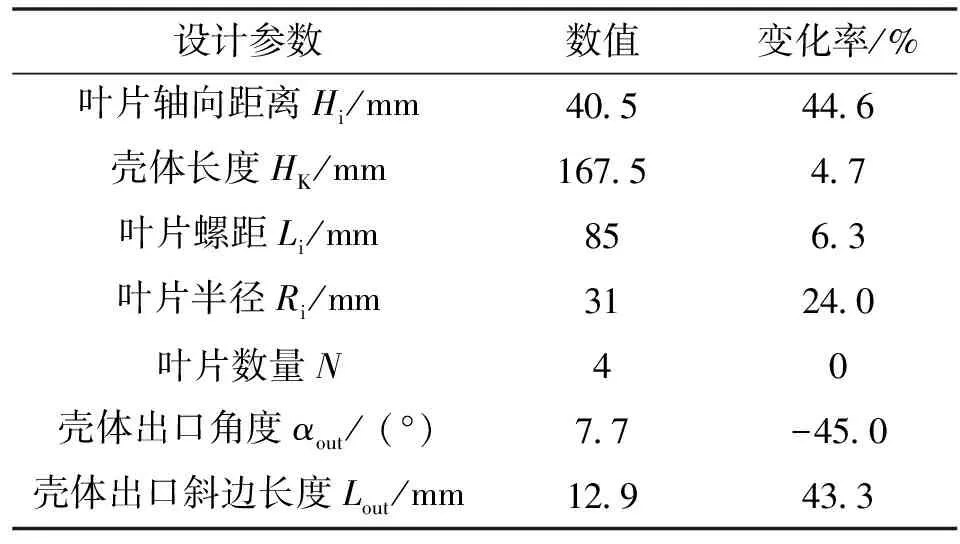
表5 方案A模型参数Tab.5 Parameters of scheme A

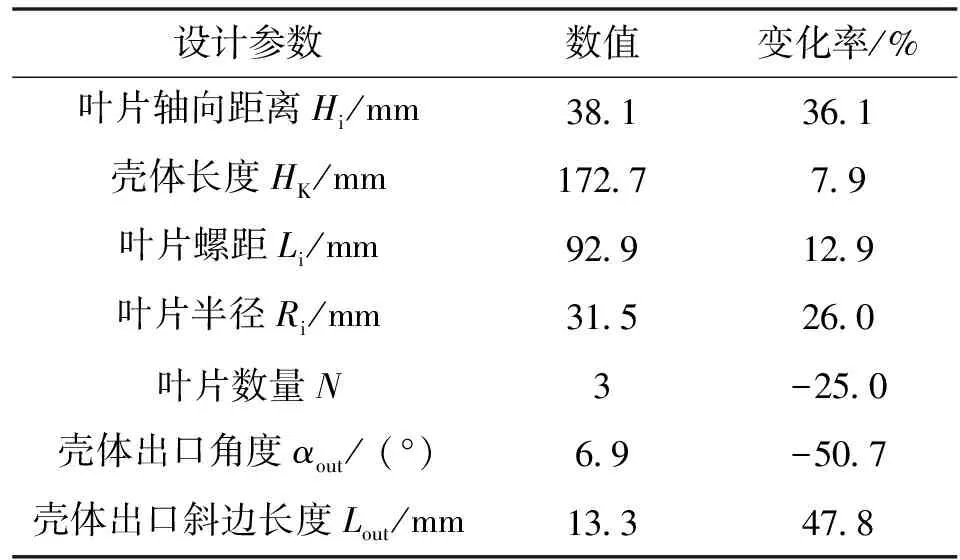
表6 方案B模型参数Tab.6 Parameters of scheme B

综合优化后模型参数变化率与原模型与优化后模型模拟数据对比结果可知：方案A与方案B的压降下降幅度分别为17.7%、31.4%，其壳体出口角度αout的变化率分别为-45.0%、-50.7%，且变化率最高，这也验证了灵敏度水平分析中压降对αout依赖性最强。

3.2 静压力分析

优化前、后YZ截面的静压力云图和L1、L2、L3截面处的静压力分布分别如图11、图12所示。

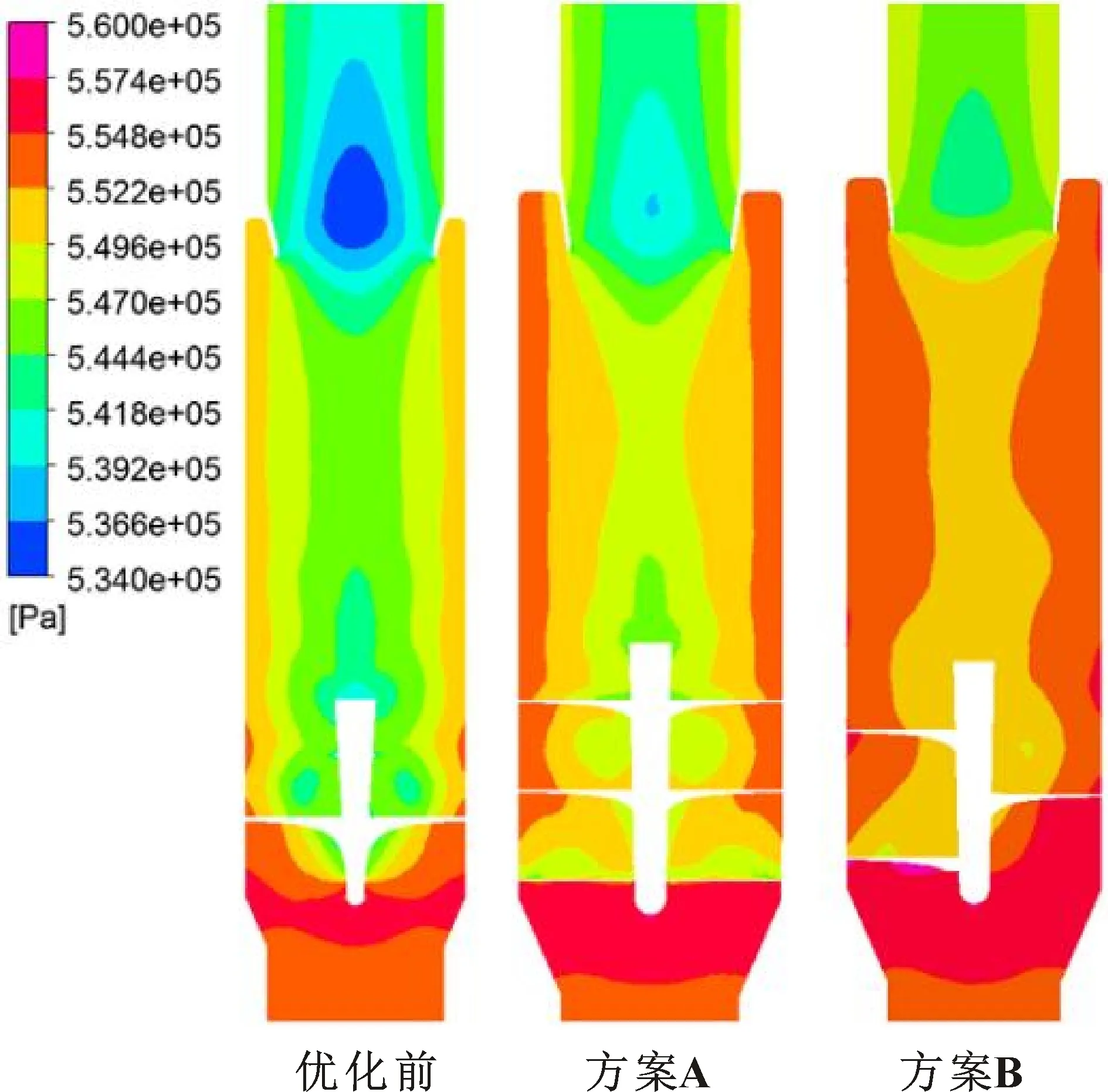
图11 优化前后YZ截面的静压力云图

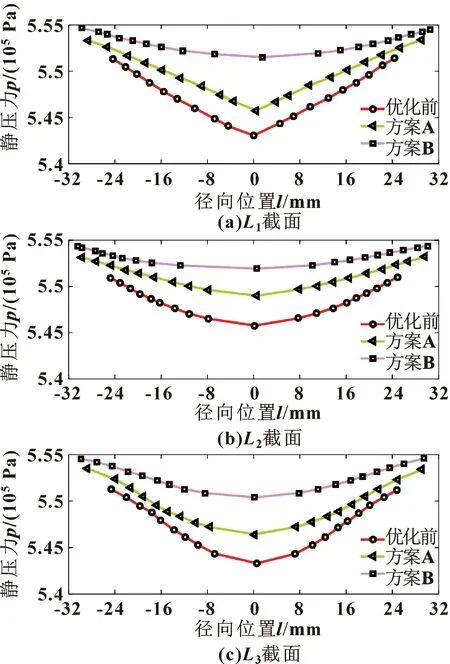
图12 优化前后静压力分布

从图11可以看出：优化前、后的静压力由壁面到中心均呈下降趋势，叶片半径Ri增大后，气相过流面积增大，流速差减缓，壁面压力损失减少，其中方案B的壁面压力损失更小。从图12可知：优化后沿径向内外旋流的压力均大于优化前，其中方案B内外旋流的压力大于方案A。优化后的气相内外压差减小，增强了流动稳定性，L3截面中方案B的径向压力变化趋势更平稳，表明接近出口的气相旋流相对稳定，压力损耗少。结合壳体参数变化率可知，相比于原模型，优化方案的壳体出口角度αout减小，壳体出口斜边长度Lout增大，沉积区域变大后有效改善了旋转气流直接汇入出口的现状，使得沿轴向内外旋流的压力梯度变小，可有效降低压降。

3.3 湍动能分析

优化前、后YZ截面的湍动能云图和L1、L2、L3截面处的湍动能分布如图13、图14所示。

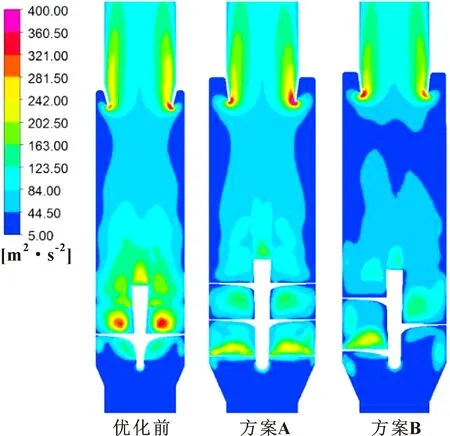
图13 优化前后YZ截面的湍动能云图

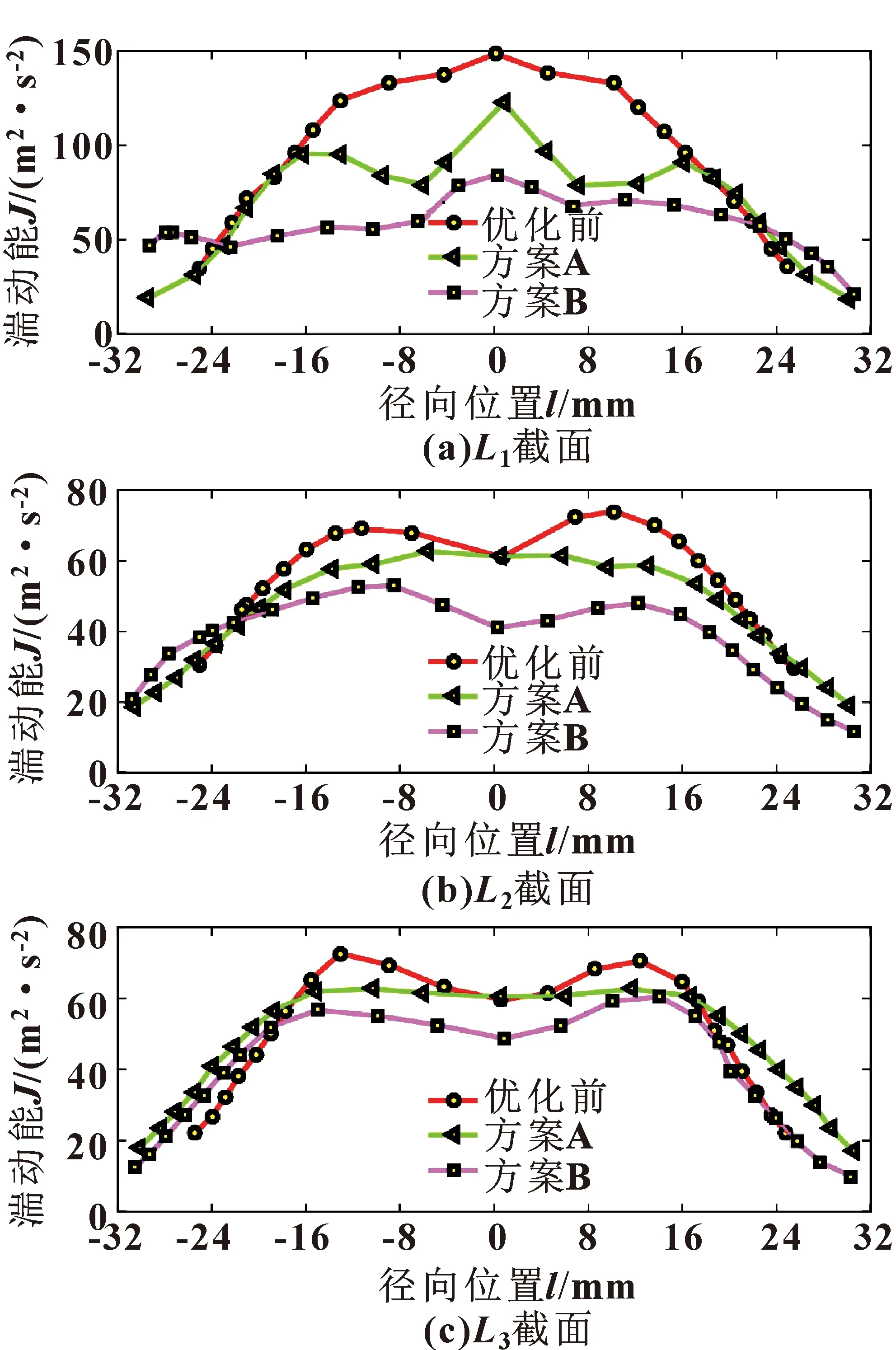
图14 优化前后湍动能分布

由图13可知：优化前导叶处的湍动能值大于优化后。由图14可知：L1截面处的湍动能值均较大，该处流动相对紊乱导致压力损耗。方案B中各截面湍动能值较小，表明该方案的旋流能量损失较小。方案A的湍动能曲线相对平滑，表明流动相对平稳且分离效率较高。结合导叶参数变化率可知，含尘气流经导流叶片加速旋转，当叶片轴向距离Hi增加后，气流旋转能量的传递状态更稳定，涡流能量得以维持，表明优化后的参数配置可有效减弱内部湍流运动强度和能量损耗，有利于提升分离效率。

综合灵敏度分析与流场分析可知，50%的结构参数变化及交互作用对导叶式分离器内部旋转流场的分布产生强影响。考虑旋风分离器性能高效低阻的需求，方案B为最优方案。

4 试验验证

为进一步验证优化结果的可靠性，对最优方案的旋风分离器进行压降与分离效率台架试验。最优方案的压降试验结果与模拟结果对比如图15所示。可知：最优方案的压降试验数据与模拟数据误差均在3%以内，且比较贴合。最优方案的分离效率试验结果为92.09%，试验数据与模拟数据误差为4.77%。可知：压降的试验值与模拟值误差较小，但分离效率的误差偏大。主要原因为模拟过程中简化了壁面碰撞系数的设置，实际情况中各部件、各部位的碰撞系数并不相同，但总体误差在5%以内，试验结果表明优化方法可行。