基于测斜数据的桩身弯矩计算

胡国保，何祖钧，王伟亮，何 钦

（1、清远市建设工程质量检测站有限公司 广东清远 511500；2、佛山市三水区建筑工程质量检测站 广东佛山 528100；3、广东省建设工程质量安全检测总站有限公司 广州 510500）

0 引言

随着基坑开挖深度逐渐增大，简易的支撑结构已无法满足基坑安全性的要求。深基坑大部分采用排桩支护或地下连续墙支护，确保基坑稳定性。在桩支撑结构中需要监测桩身水平位移以及了解桩身受力状态，确保基坑安全并提前做出应对措施。目前多采用测斜法计算桩身水平位移，若同时利用测斜数据较为准确地计算桩身弯矩可以节省时间，快速得到初步弯矩值，判断桩身安全性。

用测斜数据计算弯矩的相关研究较多，主要方法分为正算与反算两种。正算方法为三点圆法，根据测斜计算某点以及上下相邻点3个数据，计算该点曲率，进而根据曲率与弯矩关系求支护桩或地下连续墙弯矩［1-3］。但此种方法无法计算端点处弯矩，且对测斜数据完整性要求较高。在反算法中，主要方法为最小二乘法（即多项式拟合），自然样条曲线法，光顺样条曲线法。其中杨潇等人［4］通过对地下连续墙的测斜数据拟合，对连续墙弯矩分析，评估其安全性；池秀文等人［5］通过分段三次样条曲线五点拟合支护结构变形曲线，计算所得弯矩与实际工程中的弯矩观点较为吻合；王佳贺［6］使用不同次幂的多项式拟合支护位移曲线，得到五次多项式的拟合结果较好，刘涛等人［7-8］通过最小二乘法以及刚度修正，反演地连墙弯矩，与实际弯矩结果吻合较好；王震等人［9-10］基于光顺样条法反演地下连续墙与桩身弯矩，反演弯矩与实测弯矩变化趋势相同，并且反演弯矩大于实测弯矩。

利用测斜数据计算弯矩的研究已经相对成熟，方法也相对固定，即利用曲率与弯矩的关系，间接求得弯矩。本文旨在总结目前测斜数据计算弯矩的方法与原理，对比各种方法在实际应用中的误差情况，以及分析误差影响因素，为今后工程提供相关参考。

1 测斜数据弯矩计算方法

1.1 三点圆法

三点圆法是根据三点确定一个圆，然后求得圆的曲率［1］。而曲率可以衡量支护结构的变形程度。求得曲率后计算出弯矩。三点圆法的曲率推导公式有几何法与数学推导法，其最终推导结果相同。对三个连续测斜点i-1、i、i+1，其对应水平偏移量分别为yi-1、yi、yi+1。l为测斜点间的距离，R为曲率半径，φ为曲率，w为变形位移。曲率计算及弯矩计算公式如下：

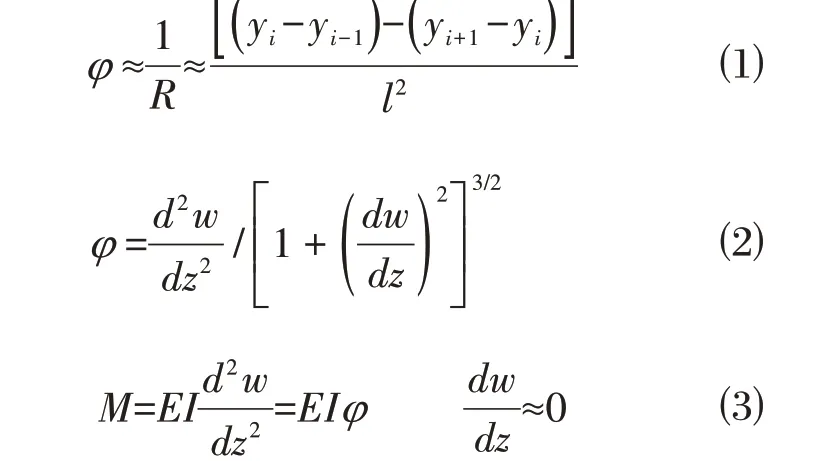
需注意的是，三点圆法计算时，无法计算支护结构两端的曲率，需要根据逼近或插值方法对得到的曲率进行拟合，求得整个深度上的曲率，因此在两端会产生较大的误差。

1.2 最小二乘法

针对一系列测斜数据（xi，yi），i=1，2，3...n。通常选取线性函数类｛x0，x，x2...xn｝。选取一定次数的多项式，求得误差平方和最小时的系数［6］，如下所示：

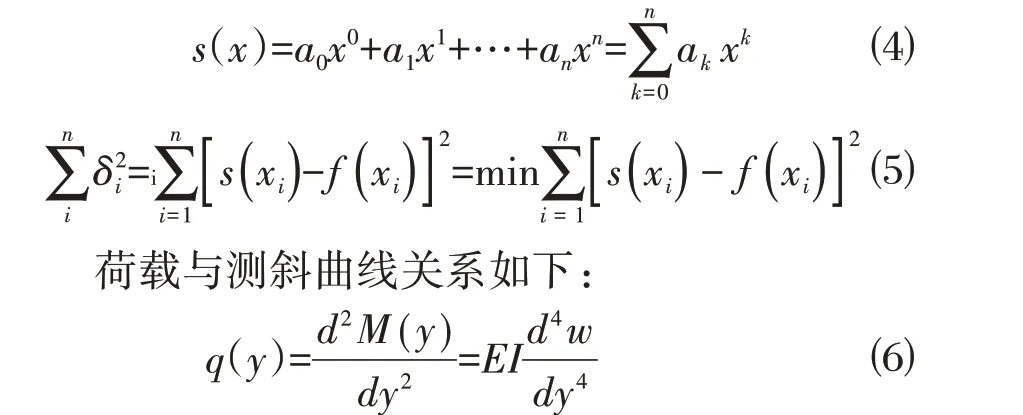
在使用最小二乘法拟合测斜曲线时，需要选取合适的多项式次数。荷载与测斜曲线呈四次方关系。弯矩与测斜曲线呈平方关系。因此次数太高易产生过拟合现象，与实际曲线形式局部吻合而其余部分偏差过大；次数太低则易与实际所受荷载情况不符。在工程中一般选取五次多项式拟合［6］，此时假设荷载呈二次分布，除此之外结合实际荷载情况也可用更高次拟合。

1.3 自然样条曲线法

使用分段三次样条函数拟合测斜曲线。此函数需满足以下条件：在每个分段内拟合函数不超过三次，在分段点上拟合函数具有连续二阶导数，最后拟合函数需要通过全部数据点并二阶连续可微［2］。

在求解符合的样条函数时，需要给定边界条件。主要有测斜曲线在测点处的一阶导数，即支护结构转角；测斜曲线在测点处的二阶导数值，即支护结构的弯矩。拟合公式如下所示：

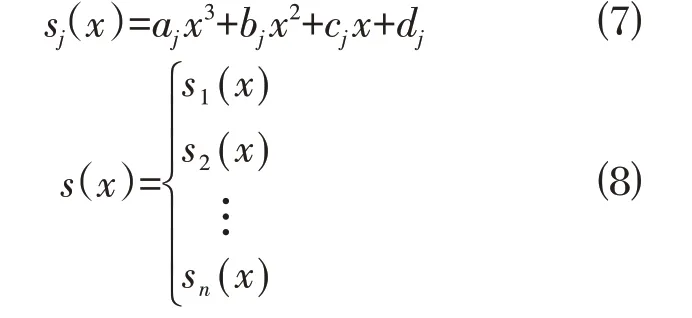
对于一系列方程s（x）包含4n未知量，根据定义条件以及边界条件可以满足条件确定唯一的样条函数。其中当边界条件为给定端点处的二阶导数值为0 时，又称为自然边界条件，此时样条函数称为自然样条函数。本文使用三次样条函数对测斜数据直接拟合，而后反算其弯矩。

2 工程实例

基于某医院边坡基坑支护所得桩身应力监测数据以及测斜数据进行计算。基坑采用钻孔灌注桩，桩长14 m，桩身直径1.4 m，桩身受力筋直径为28 mm，HRB400 钢筋。每隔0.5 m 记录一次测斜数据，每3 m记录钢筋应力计数据。采用C30 混凝土，保护层厚度70 mm。钢筋弹性模量与混凝土弹性模量比n=6.67。有效计算直径ds=1.26 m。采用6 月21 日～7 月22 日间的监测数据对比各种弯矩计算方法的准确性。

桩身混凝土未开裂时，以钢筋应力计数据反算桩身弯矩［11］。具体计算公式如下：

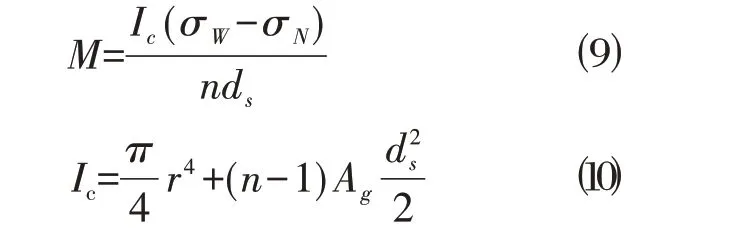
式中：M为桩身弯矩；Ic为截面中性轴惯性矩；σ W为桩外侧钢筋应力计读数；σ N为桩内测钢筋应力计读数；n为钢筋与混凝土弹模之比；ds为同一截面位置两钢筋应力计之间的距离；Ag为主筋截面积；r为桩身半径。

根据钢筋应力计求得桩身弯矩，如图1所示。

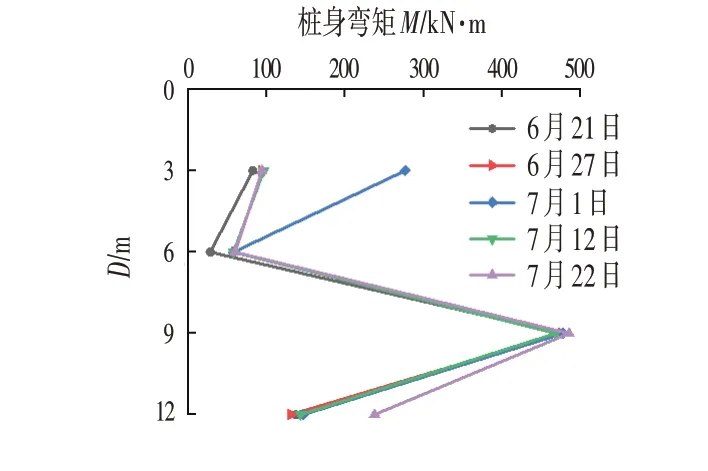
图1 钢筋计计算桩身弯矩Fig.1 Bending Moment of Pile Body Calculated by Steel Bar Meter

在所取时间段内，计算弯矩最大值接近300 kN·m，主要在桩身内侧受弯。所测时间内弯矩变化趋势相同，且根据宋建学等人［11］的研究成果，采用钢筋计计算时考虑桩身是否开裂等因素，计算弯矩值精度较高，因此取钢筋计计算所得桩身弯矩近似作为实际值，与其余方法所求弯矩对比分析。但钢筋计其缺点在于布设点位较少，无法得出整个深度上弯矩，只能测量个别点位弯矩，整体变化趋势难以判断。

多项式测斜曲线拟合图与样条曲线拟合图分别如图2、图3 所示，在整体上两种拟合曲线相似。可知多项式拟合曲线较平滑，虽未经过所有数据点，但在所取时间内拟合趋势相似，曲率变化与钢筋计测值较为吻合。样条曲线拟合虽经过数据点，但其在个别数据点曲线趋势变化较大，且计算后曲率变化大，计算弯矩远远偏离实际值。

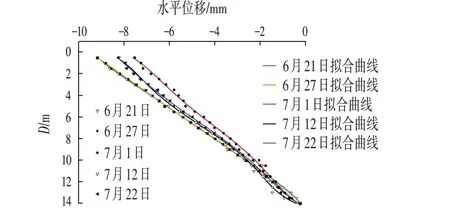
图2 多项式拟合测斜曲线Fig.2 Polynomial Fit Inclinometer Plot

图3 样条曲线拟合测斜曲线Fig.3 Spline Fit Inclinometer Plot

当采用三点圆法计算弯矩时，首先采用计算点与相邻三点计算曲率，而后根据弯曲刚度求得弯矩。计算所得弯矩与钢筋计计算所得数据相差大。最大弯矩值相差近10倍。除此之外，三点圆法无法求得两端弯矩，且所得曲率与测斜数据准确度以及测斜间距分布关系较大，若测斜值出现偏差，则会导致相邻点弯矩同时出现偏离现象。根据对本工程数据拟合结果，三点圆法其稳定性差，与实际值存在2～10 倍差距。因此在实际计算中应根据实际情况判断是否使用此方法。

图2为多项式拟合后曲线。采用最小二乘法时需要选取合适的多项式。根据位移曲线与荷载关系，当位移曲线为三次多项式时，荷载为集中力，而当位移曲线为五次多项式时，荷载呈线性分布。根据桩身所受土压力以及相关经验［6］选取五次多项式拟合测斜数据，假定土压力线性分布。对拟合多项式二次求导后得到曲率并计算弯矩。多项式拟合数据在量级上与钢筋计测值较为接近，在整个深度范围内均与实际值较为吻合。且在所选时间内数据拟合效果均稳定，仅在两端弯矩值偏大。

图3为采用三次自然样条法拟合测斜数据计算弯矩。每两点之间均采用三次多项式进行拟合，且拟合后数据经过采样点。根据拟合结果，在所测时间内偏差均远超实际值。其原因在于三次样条虽然可以很好拟合测斜数据，但二阶求导后，其曲率函数为一次函数，即弯矩与荷载呈线性变化，与实际情况相差较大。除此之外，直接采用三次样条插值，使得在每两个测点数据之间曲率变化不连贯，造成弯矩值变化也较为反常。根据本工程实际数据，直接采用三次样条对位移函数插值结果并不适用，且若考虑分段插值时需分清各段的受力状态，在实际应用中存在较大难度。

6 月21 日～7 月22 日各种方法所得弯矩如图4 所示。可知，三种方法所得弯矩均与钢筋计所测弯矩值存在较大偏差，且在支护桩两端时弯矩均大于桩身中部弯矩值，在中部弯矩偏向于集中分布。采用三次样条拟合时，虽拟合曲线经过数据点，但其求导后偏差巨大。在计算数据中最大弯矩已远远超出实际值，最大弯矩值接近实际值数倍，甚至已达破坏状态下的弯矩。且弯矩变化剧烈，连贯性差。三点圆法计算弯矩最大值接近实际值的10余倍；但在3～9 m 深度处拟合效果较好，虽存在一定偏差，但与实际值较为接近，但其在不同时间段内偏差较大，无法保证其稳定性。采用多项式拟合时，根据相关文献以及实际土压力分布选取五次多项式［6］，所得弯矩最大值接近实际值的2倍，且在深度范围内拟合效果较好，在与钢筋计对应点位上弯矩值相近，与实际受力情况较为相符。

图4 弯矩图Fig.4 Bending Moment Diagram

3 结论

根据实际工程数据拟合结果可知，三点圆法计算测斜数据曲率时，由于其受数据准确率、偶然误差的影响较大，会导致计算结果偏离实际值，且计算结果不稳定，相邻时间内计算结果也存在较大误差。多项式与样条拟合测斜数据时，拟合曲线相似，但求导后曲率相差较大。多项式拟合计算结果与实测值吻合程度高，且稳定性较高，在所选时间内都未出现较大误差。样条拟合虽可以很好拟合测斜，但其曲率变化幅度大，导致计算弯矩远超实际值。因此结论如下：

⑴三点圆法与样条拟合所得弯矩与实际值相差大，不建议在实际工程中使用。

⑵五次多项式拟合效果较好，所得弯矩与实际弯矩值吻合程度高，在实际工程计算中有一定参考意义。