改进鲸鱼优化算法的微电网混合储能容量配置研究

邓 坤， 温拥军， 胡 攀， 郭永强

(1 贵州大学 电气工程学院， 贵阳 550025； 2 浦江光远电力建设有限公司， 浙江 浦江 322200)

0 引 言

微电网中，源、荷间的不平衡功率给电网的稳定运行带来了巨大的挑战，引入储能系统可有效应对这一问题[1]。混合储能(Hybrid Energy Storage System，HESS)相比单一储能装置，能够同时满足微网对功率及能量的需求。

当前，国内外已有较多文献针对由蓄电池与超级电容构成的混合储能进行研究。如：文献[2]中采用傅里叶变换对净负荷功率进行频谱分析，得出混合储能系统充放电功率指令，有效平滑微电网净负荷功率波动性。文献[3]配置混合储能，平滑微电网联络线功率波动，采用傅里叶变换波动功率进行分析。文献[4]基于风电并网功率波动标准，采用自适应小波包分解方法，处理风电场不平衡功率，对超级电容和锂电池的功率进行分配。以储能系统年综合成本最小为目标，建立考虑电池寿命衰减的混合储能容量优化配置模型，确定最佳储能系统的功率和容量配置以及相应的频率分界点。小波分解能够对非线性信号进行较好的分析，但若基波选择不当则会影响最终的分析结果。文献[5]建立混合储能容量双层配置模型，采用经验模态分解(Empirical Mode Decomposition, EMD)风电功率，由全钒液流电池平抑不满足并网波动要求的高频功率，压缩空气储能参与风电并网日前调度运行。文献[6]提出一种基于变分模态分解和希尔伯特变换(VMD-Hilbert, VMD-H)的 HESS 平滑光伏发电输出功率波动策略，结合储能系统 SOC ，并参考值偏差确定模糊控制规则，修正各个储能元件的充放电功率。VMD能够减小模态混叠，但若分解层数选择的过大或者过小均会加剧模态混叠。虽然EMD在分解非平稳信号时存在模态混叠，但因其原理简单易于实现，目前被广泛应用于电力行业中。

本文配置混合储能系统平抑微电网中的不平衡功率，以配置综合成本最小为目标，计及储能元件的充放电效率，构建混合储能容量优化配置模型。利用经验模态分解算法(EMD)将储能系统总功率分解，由超级电容平抑高频功率，蓄电池平抑低频功率。同时改进传统鲸鱼优化算法，采用幂函数控制参数，增强算法在寻优时跳出局部最优解的能力，同时引入自适应权重因子，提高算法的寻优能力。

1 微电网结构

微电网通常是与电网相连处于并网模式，并且与主网进行功率和信息的交互。但由于地域原因微电网无法与主网相连接，或发生较大故障时微电网自行和主网断开形成了独立型微电网。

在独立运行时，分布式电源和储能系统协同供给微电网中的负荷。根据汇流母线的不同，可将其分为直流、交流、交直流混合微电网。在直流母线微网中，分布式电源与储能是经过变换器接入母线的。本文选择直流母线的独立型微电网建模分析，其结构如图1所示。

图1 微电网结构

其中，pw(t)为风力发电机组的总输出功率；Pv(t)为光伏发电输出的总功率；phess(t)为混合储能系统的输出功率；pbat(t)为蓄电池输出功率；psc(t)为超级电容输出功率；pl(t)为负荷功率。

独立微电网中的不平衡功率也称为净负荷功率，为负荷需求与风力发电、光伏发电之和的差值，如式(1)、式(2)所示：

pun(t)=pl(t)-pw(t)-pv(t)

(1)

phess(t)=psc(t)+pbat(t)

(2)

2 混合储能功率分配与容量优化

2.1 基于经验模态分解的功率分配

EMD适合对非线性信号进行分析，将初始信号x(t)根据不同的时间尺度特征，分解为一系列的固有模态分量(intrinsic mode function, IMF)，如式(3)所示：

(3)

式中：IMFi(t)为初始信号x(t)的第i阶固有模态分量，物理意义则是初始信号x(t)的一种波动模式，I(t)为残余分量。

对储能系统总功率进行经验模态分解，得到频率由高到低的N阶IMF。超级电容可以快速充放电，功率密度大，能够处理高频波动功率；蓄电池响应时间较长，能量密度较大，适合处理能量高的低频波动功率。超级电容的充放电功率指令为高频波动部分，如式(4)所示：

(4)

蓄电池的充放电功率指令则是低频波动部分，为D+1阶IMF到残余项之和，如式(5)：

(5)

2.2 混合储能额定功率、容量

超级电容与蓄电池的充放电功率指令分别为psc(t)、pbat(t)，所配置的超级电容与蓄电池额定功率应能在t时刻吸收最大的剩余功率或者补偿最大的功率缺额。计及储能元件的充放电效率，超级电容的额定功率为：

(6)

其中，ηd、ηc分别为超级电容的放电、充电效率；t0为初始时刻。蓄电池的额定功率pBN(t)同理可求得。

参考文献[7]中对超级电容与蓄电池的最小额定容量的推导过程，其最小额定容量为：

(7)

3 混合储能容量优化配置模型

3.1 目标函数

混合储能容量优化配置的目标为系统年综合成本最小，综合成本由等年值投资成本Ccap与风险惩罚成本Cpun组成。其中，等年值投资成本包含储能的购置成本Cinv、维护成本Cmain、系统更换成本Crep等。因此，在重构EMD分解得到的N个固有模态分量时，以等年值投资成本最小选择滤波阶数D，确定蓄电池与超级电容的充放电功率指令。目标函数如式(8)：

minF=Ccap+Cpun=Cinv+Crep+Cmain+Cpun

(8)

(1)混合储能购置成本:

Cinv=(cPbatPBN+cEbatEBN+cpcapPCN+cEcapECN)γ

(9)

(10)

式中：cPbat、cEbat分别为蓄电池单位功率和单位容量的投资成本，cpcap、cEcap分别为超级电容单位功率和单位容量的投资成本，PBN、EBN分别为蓄电池的额定功率、容量，PCN、ECN分别为超级电容的额定功率、容量，r为投资折现率，TN为储能系统的额定使用年限。

(2)全寿命周期内储能系统的更换成本:

Crep=γ(cPbatPBN+cEbatEBN)nb

(11)

由于超级电容充放电寿命达到几十万次甚至上百万次，在配置期间不考虑寿命损耗。然而，蓄电池使用损耗较大，nb为更换次数[8]。

(3)混合储能系统维护成本:

Cmain=yscECN+ysbEBN

(12)

式中：ysc、ysb分别为超级电容器、蓄电池单位容量的年均维护成本。

(4)系统切负荷、弃风、弃光惩罚成本:

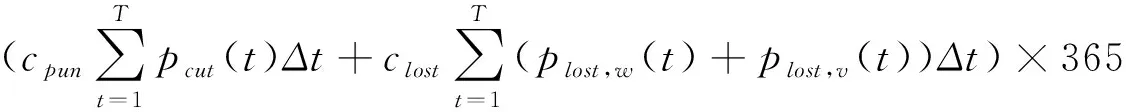
(13)

式中：pcut(t)为t时刻系统切负荷功率，plost,w(t)、plost,v(t)为t时刻弃风、弃光功率，cpun为切负荷单位惩罚成本，clost为弃风弃光单位惩罚成本。

3.2 约束条件

(1)系统允许出现功率缺额，但也要保证系统供电可靠性，因此要保证各时段切负荷电量不能超过最大值。

(14)

(2)为保证新能源消纳，不能出现大量的弃风、弃光。因此，需要保证各时段弃风、弃光量不能超过最大值。

(15)

4 改进鲸鱼优化算法

配置混合储能系统，平抑微电网系统中的净负荷功率是一种非线性规划问题，而WOA作为群体智能算法中的新型算法，虽具有原理新颖、结构简单、优化效果突出、搜索能力强，并在求解非线性问题上具有一定优势，但在跳出局部最优、平衡全局搜索能力与局部开发能力等方面仍存在缺陷。因此，本文引入非线性控制参数与自适应权重增强全局搜索能力改进鲸鱼优化算法，采用改进鲸鱼优化算法(Improved Whale Optimization Algorithm, IWOA)对模型求解。

4.1 鲸鱼优化算法

4.1.1 包围捕食阶段

在包围阶段，鲸鱼群体相互传递猎物所处的位置信息，使整个群体不断朝着最接近猎物的鲸鱼个体移动；而距离猎物最近的鲸鱼个体再通过随机搜寻，进一步缩短与猎物的距离，从而逐渐收缩包围圈、靠近猎物。猎物的位置信息即所求问题的最优解。

鲸鱼种群包围捕食阶段的数学模型为：

D=|CXP(k)-X(k)|

(16)

X(k+1)=Xp(k)-AD

(17)

其中，k为当前迭代次数；X(k)为当前鲸鱼的位置向量；Xp(k)代表当前最优鲸鱼的位置向量。而A、C系数向量的数学模型可以表示为：

A=2a·r1-a

(18)

C=2·r2

(19)

其中，r1和r2为[0,1]间的随机数，a是随迭代次数的增加，从2线性递减到0的控制参数。其数学模型表示为

(20)

其中，Max_iter代表最大迭代次数。

4.1.2 螺旋更新阶段

在此阶段，鲸鱼围绕猎物不断地螺旋游走、逼近猎物，以此达到最终捕获猎物的目的。其数学模型可以表示为

X(k+1)=Deblcos(2πl)+Xp(k)

(21)

其中，b是限制对数螺旋形状的常数，l为[0,1]间的随机数。

4.1.3 猎物搜寻阶段

为提高全局搜索能力，鲸鱼个体需要随机搜索猎物。在此过程中，鲸鱼个体通过|A|的值来判断是搜索猎物阶段还是包围捕食阶段。当|A|≥1时，鲸鱼个体在收缩包围圈的同时进行随机更新。这种策略在很大程度上可以使每个个体远离当前最优解，从而具有较强的跳出局部最优的能力。则猎物搜寻阶段的数学模型可以表示为：

D=|CXrand(k)-X(k)|

(22)

X(k+1)=Xrand(k)-AD

(23)

其中，Xrand(k)为当前鲸鱼种群中随机个体的位置向量。在参数|A|取其他范围时，鲸鱼个体进行局部搜索，选择螺旋方式进行位置更新。

4.2 改进鲸鱼优化算法

根据WOA算法原理可知，通过调节参数|A|的大小，来平衡全局搜索与局部搜索能力。而参数|A|主要取决于控制参数a的变化，a越大则参数|A|≥1越有可能发生，则算法的全局搜索能力越强；同理a越小，算法的局部搜索能力越强。控制参数a以线性函数减小，算法仅迭代至中期，此时参数a已经减小了一半，全局搜索能力下降迅速，容易陷入早熟。

针对上述问题，本文采用幂函数来控制参数a。搜索前期参数a缓慢减小，其值仍然较大，提高算法全局搜索能力，迭代后期参数a迅速减小至0，增强局部搜索能力为

(24)

式中：t表示当前迭代次数，Max_iter为最大迭代次数。

文献[9]表明，权重因子ω(t)对平衡全局搜索与局部搜索有较强的指导作用。当ω(t)较大时，寻优的种群能够在更大的空间内寻找最优值，侧重于全局搜索；而当ω(t)较小时，能够在较小范围内进行高精度搜索。为了提高WOA寻找最优解的能力，采用指数函数控制的自适应权重因子，利用其更新寻优位置。权重位置调整数学模型为：

(25)

(26)

由式(26)可知，在迭代前期ω(t)的值减缓较慢，意味着参与调整的值较大，全局寻优能力较强；到了迭代后期，ω(t)减小较快直到最终为0，算法的局部寻优能力较强。同时采用随机差分变异，增加群体个体的多样性。本文以综合配置成本最优为目标，采用IWOA算法求解混合储能总出力，得到储能系统最优出力。

5 算例分析

以中国贵州某地区的风光互补微电网为例，选取该地区典型日风光出力以及常规负荷用电，采样间隔5 min，出力曲线如图2所示。其中，系统参数参考文献[10]。

图2 典型日风光荷出力

采用EMD算法对混合储能出力的分解结果如图3所示。由此可见，IMF1为功率波动最迅速的分量，IMF2～IMF6功率的波动依次减缓，对应的瞬时频率曲线依次降低，各IMF能够较好的反映出储能总出力的波动特性。

图3 EMD分解结果

5.1 配置结果分析

普通鲸鱼算法与改进鲸鱼算法的优化配置结果见表1。从表1可以看出，采用IWOA算法综合配置成本，相比采用WOA算法降低了3.02万元；超级电容的额定容量相比较IOWA算法寻优结果高出2.52 kW·h，表明IWOA算法具有更强的寻优能力。

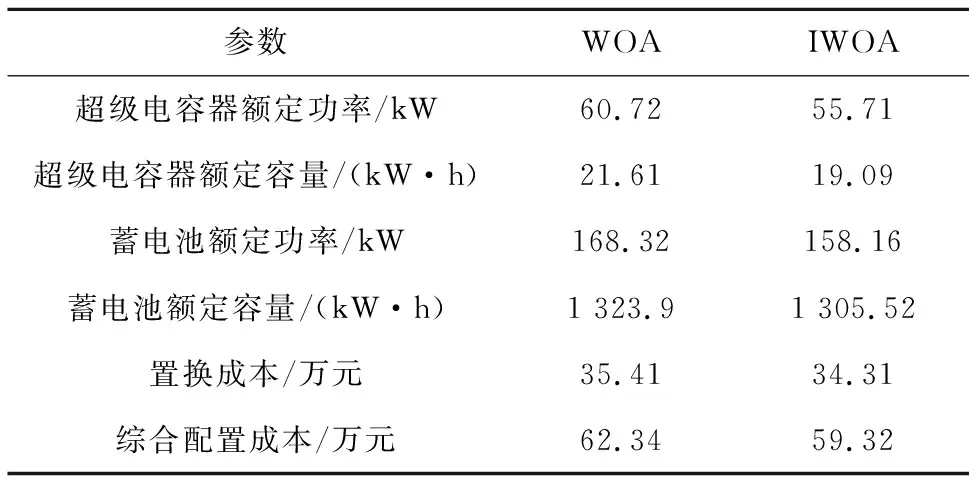
表1 配置结果

分别采用普通鲸鱼算法与改进鲸鱼算法对比，寻优收敛曲线如图4所示。可以看出，普通鲸鱼算法迅速收敛，迭代至50代，最优值基本不再变化，陷入局部最优。改进鲸鱼算法，由于幂函数控制参数a(t)、权重因子ω(t)，在迭代前期仍然较大，更有利于寻优时跳出局部最优解，能够在更大的范围内寻找最优解，表明改进鲸鱼算法比普通鲸鱼算法的寻优能力更强。

图4 收敛曲线

5.2 功率分界点对配置结果的影响

不同功率分界点下系统配置综合成本如图5所示。当分界点D=0时，只配置蓄电池；D=7时只配置超级电容器。系统配置综合成本随着分界点的增加，呈现先减小后增大的趋势。功率分界点越小，蓄电池承担的不平衡功率越大，而低频功率变化较快，蓄电池的充放电次数频繁，减少了电池的使用寿命，增加了更换成本。功率分界点越大，超级电容承担的不平衡功率越大。当分界点为7时只配置超级电容，大大增加了超级电容的额定容量。由于电容器的单位容量成本较昂贵，因此配置综合成本大幅度提高。

图5 系统综合配置成本-功率分界点关系

当功率分界点D=3时，系统综合配置成本最低。可见，配置混合储能相比单一储能成本更低，混合储能充分发挥了不同储能介质的充放电特性以及经济优势。

图6为蓄电池与超级电容器充放电功率。由图中可见，蓄电池承担不平衡功率波动较为缓慢部分，而超级电容承担不平衡功率中波动较为频繁部分，所需容量较小，符合超级电容的充放电特性点。蓄电池充放电功率与原不平衡整体趋势相同，所需容量较大，能够发挥蓄电池单位容量价格较为经济的优势。

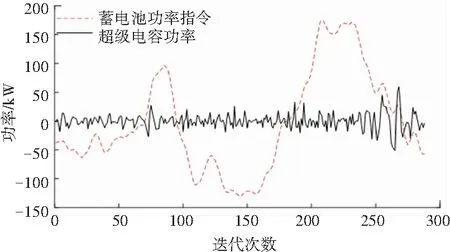
图6 蓄电池与超级电容器充放电功率

6 结束语

本文对于独立型微电网，考虑不同储能设备的充放电特点，对微电网中的不平衡功率进行分解，配置混合储能，相比较配置单一储能设备能够有效降低系统配置综合成本。对于所构建的模型，采用改进鲸鱼优化算法求解，增强了算法的全局寻优能力，提高了算法的求解精度。