基于时序数据挖掘的铝电解槽工艺参数优化研究

2023-02-27张显国王明刚

智能计算机与应用 2023年2期

张显国，曹斌，王明刚，石进

(1 贵州大学大数据与信息工程学院, 贵阳 550025; 2 中铝智能科技发展有限公司技术部, 杭州 310000;3 遵义铝业股份有限公司分析计控中心, 遵义贵州 561300)

0 引言

铝电解槽基本由4个部分组成：阴极结构、上部结构、母线结构以及电气绝缘部分。为保证电解槽安全稳定生产，需要工艺参数处于正常范围，如：电流、槽电压、极距、电解温度、电解质水平、加料次数等。由于电解铝生产环境的恶劣因素，如：强磁、高温、多粉尘和空间狭窄等，导致普通传感器不能在该环境下稳定运行，不能获取更多精准数据，如：分布电流、阴极温度和炉膛厚度等。目前能获取到的数据为单槽电流、单槽电压和一些原辅料下料量等间歇性测量和化验数据。

为提高铝液的产量和质量，挖掘物料、能耗等数据之间的关联性并建立铝电解反应模型具有重要意义。文献[1]提出使用数据挖掘技术得到平均电压、工作电压和效应持续时间之间的线性关系；文献[2]提出基于统计学方法控制电解槽的热量平衡；文献[3]提出基于贝叶斯网络的异常塑因模型。本文研究铝电解反应过程中的下料时序数据和生产工艺参数的时序数据，通过数据挖掘的方法，对铝电解槽内物料平衡和热量平衡建模，合成完整的铝电解槽反应过程模型。

1 相关工作

铝的电解化学反应式：

可知保持合适的物料平衡，一定范围内提高氧化铝浓度，可以提高铝的产量。

铝冶炼的出铝量AL，公式(1)：

(1)

由公式(1)可知，在适宜的能量平衡下，提供电流值、电流效率或效应时长能够提高铝的产量。

通过数据挖掘方式获得物料平衡和能量平衡之间关联性，为防止后期数据挖掘出现虚假回归问题，先对所有序列进行平稳性检验。单位根检验(Augmented Dickey-Fuller test)是迪基-福勒检验(Dickey-Fuller test)的增广形式，其无漂移项回归公式如公式(2)所示：

(2)

其中，Δ为增量；εt为t时刻残差(白噪声)；βi是i阶自回归加权系数。

假设H0:δ=0，若检验序列存在单位根，则检验序列为非平稳序列，否则为平稳序列。

两个时间序列使用皮尔逊相关系数法需要满足以下条件：两个时间序列长度一致，连续且服从正态分布，因此首先检验时间序列是否服从正态分布，因为单维时序数据序列的样本数小于5 000，所以采用夏皮罗-威尔克(Shapiro-Wilk)检验，根据检验结果检验序列是否服从正态分布。

夏皮罗-威尔克检验：单维时序数据序列是一个样本数为n的样本，假设H0：样本序列与正态分布没有显著区别，H1：样本数据与正态分布有显著区别[4]。检验使用的统计量W定义为公式(3)：

(3)

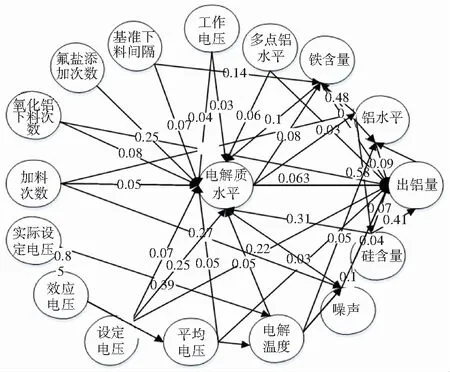
获得统计量后，设定显著性水平α，获取其分位数或者临界值Wα，若W

为降低格兰杰因果检验的计算复杂度，首先计算时序序列集合的相关系数集合。在指定时间段内，多维时序数据序列在时间段内k维时序数据序列之间的相关系数集合为KR[5]，公式(4)：

(4)

其中，Rij表示i,j序列之间的相关系数值。

为了减少非线性关系分析的计算复杂度，先进行因果检验，获得序列之间的因果关系。格兰杰因果关系检验是一种推断和分析两个时间数据序列之间是否存在逻辑因果关系的检验算法[5]。检验序列X和检验序列Y在T时刻数值为XT和YT，公式(5)和公式(6)：

(5)

(6)

其中，Xi是序列X在i时刻的数值;Yi是序列Y在i时刻的数值；u1和u2为不相关的白噪音；α,β,λ,δ为参数。

若式(5)成立而式(6)不成立，则序列Y是引起X变化的因序列，存在序列Y到X的单向因果关系；若式(6)成立而式(5)不成立，则序列X是引起Y变化的因序列，存在序列X到Y的单向因果关系；若式(5)、式(6)同时成立，则认为X和Y存在双向因果关系。

为进一步理解因果变量之间的非线性程度，采用非线性回归分析方法，得到因变量和多个果变量的非线性回归系数集合。有助于关键参数的优化决策。梯度提升回归树有着较强的泛化能力，对异常值有很好的鲁棒性，以决策树为基函数，采用基函数的线性组合与前向分布的提升方法，其基本思想是采用多个弱分类器构建一个强分类器[6]。

为获取影响出铝量的工艺影响参数路径图，基于图论和概率论以及贝叶斯网络的理论，构建有向概率无环网络图，其中节点表示铝电解槽的某个生产条件变量，有向边表示变量之间存在单向或者双向因果系。设有图G=(V,E)，其中V={v|v∈Sk}，E={e|e∈(Rij=1)}，顶点v表示变量，路径e表示两个变量存在因果关系，箭头方向表示单向或者双向因果，节点概率值表示特征重要性程度[7]。

2 算法流程

首先，进行时序数据序列空值填充、重复值删除等预处理；其次，将满足正态分布的序列集合做皮尔逊相关处理，具有相关性的变量相互间进行格兰杰因果分析并得到因果变量集合，将满足平稳性的因果变量集合做非线性回归分析，得到因变量和多个果变量的非线性回归系数集合，对于不满足正态分布的变量、不满足平稳性的变量和其他没有相关性的变量在图中用孤立节点表示，最后将节点和工艺参数名对应并输出铝槽模型。

算法的具体流程如图1所示。

图1 算法流程图

3 实验

3.1 数据处理

从铝厂的时序数据库中导出若干个铝电解槽的工艺参数的数据变量，包括日期、槽号、槽状态、运行时间、设定电压、工作电压、平均电压、效应电压、效应持续时间、效应次数、电压摆时间、异常持续时间、氧化铝下料次数、加料次数、氟盐添加次数、出铝指示量、基准下料间隔等。数据清洗方法如下：

由于传感器延迟传输导致的重复样本，本文根据时间戳保留第一个时间戳样本，删除其余重复样本；

若当前时间戳的工艺参数记录值缺失数量过多，则删除该样本，否则就采用众数填充的方式填补缺失值；

某些样本的某些属性值超出或者低于正常范围，为了保留真实的生产数据，不处理异常值并保留该样本。

3.2 挖掘序列性质

计算和获取单维时间序列的平稳性和正态性。采用单位根检验，检验的显著性结果p<0.05，则该序列是平稳的时序数据序列。采用夏皮罗-威尔克方法检验每个时间序列，若统计量W小于Wα，则检验序列符合正态性分布。根据检验结果的峰度、偏度以及图像形状判断序列是否满足正态分布，若序列峰度绝对值小于10和偏度绝对值小于3，并且相应正态分布直方检验图呈现中间高，两边低的钟型，就判定检验序列符合正态分布。

3.3 挖掘序列关系

(1)相关关系。为获取多维时间序列之间的相关系数集合，将满足正态分布的数据集做皮尔逊相关系数处理。

(2)因果关系。为了判断两个工艺参数相互之间是否存在逻辑因果关系，选取具有相关性的时间序列进行格兰杰因果检验。实际设定电压和实际出铝量时间序列具有不平稳性，但在铝生产过程和指导出铝过程中具有重要意义，因此两个序列也要和其他序列做因果分析。

(3)非线性关系。使用梯度提升回归树算法计算影响果变量的各个因变量权值，数据集按照8:2划分训练集和测试集。梯度提升回归树节点分割的准则为弗里德曼均方误差[8]，决策树的最大深度为10，内部节点再划分所需最小样本数为2，叶子节点最小样本数为1，叶子节点样本最小权重为0，最大叶子节点数为50。

根据每一组因果关系，梯度提升回归树获得非线性回归关系。

3.4 物料能量平衡模型

基于获得的因果关系集合和因果权值集合，构建贝叶斯网络结构。贝叶斯网络中的“节点”代表工艺参数，“有向边”代表两个工艺参数的因果关系，权值代表当前因变量影响果变量的程度。出铝关系图如图2所示。

图2 出铝关系图

4 实验结果与结论

4.1 评价指标

为了定量分析模型对出铝量的拟合回归效果，采用可决系数R2、平均绝对误差(MAE)和均方根误差(RMSE)作为评价指标。

可决系数R2值在[0,1]之间，数值越小代表模型越好，式(7)：

(7)

平均绝对误差(MAE)，数值越小表示错误越小，模型越好，式(8)：

(8)

均方根误差(RMSE)是在均方误差基础上求取平方根，式(9)：

(9)

4.2 出铝量拟合结果

采用广度优先搜索算法，搜索出直接影响出铝量的直接节点，强相关关系系数阈值为0.1，强因果关系的特征重要性程度阈值为0.05。搜索出直接影响出铝量的因果关系，见表1。得到氧化铝下料次数，加料次数、设定电压、针振、铝水平、电解质水平、铁含量、硅含量和出铝量的强相关系数绝对值在0.126和0.331之间，强因果关系的特征重要性程度在0.07和0.22之间。出铝因果关系表体现的物料平衡因果关系和公式(1)的化学反应方程表达的物料平衡结论基本一致。氧化铝下料次数和加料次数是氧化铝(Al2O3)和碳(C)的主要来源，频繁向电解槽添加适量的氧化铝，使得电解质中保持适当的氧化铝浓度和铝水平，提高铝的产量；电流和工作电压直接存在强相关关联。一定条件下，提高电压，从而提高电流，也能够提高铝的产量，和公式(2)表达的改变热量平衡来增加铝产量结论基本一致。