模糊时间窗下考虑动态需求的生鲜路径优化

顾艳鑫， 赖红波

(上海理工大学 管理学院， 上海 200000)

0 引 言

近年来人民生活水平提高、可支配收入形势向好，对高品质生活的追求愈加强烈，比起常温长保质期的产品，人们更倾向于选择冷藏短保的蔬菜、水果、奶制品等产品。然而，由于生鲜购买是高频次的即时性消费，消费者在生鲜送达的时效性和新鲜度层面对生鲜零售商的物流水平提出高要求。因此，对车辆路径优化问题的研究具有十分重要的现实意义。

车辆路径优化问题(Vehicle Routing Problem，VRP)最早由Dantzig等人[1]于1959年提出，自后对于该问题的研究层出不穷，并取得了丰硕的研究成果，研究趋势给后人提供了参考价值。

在建立车辆路径优化模型时，要更加贴近现实条件，并考虑多种影响因素进行综合优化，将VRP问题进行拓展，多级VRP问题就是在客户与配送中心之间建立一个或多个物流中心。如：Chen等[2]对药品分配了一种广义多级优化方法；Dai等[3]继续开发三级、四级方法，以求在更短时间内得到解。为响应碳中和政策，更多地考虑碳排放因素，Shen等[4]、Qin等[5]通过计算碳排放交易机制量化成本，考虑不同的碳价格和碳配额。近几年的研究已从静态考虑多种因素转变到因素的动态变化上来。一种考虑动态需求的主流求解方法是两阶段模型法。如：张文博[6]将通过两阶段规划，在初始规划后将动态需求转化为多个瞬时静态子过程；范厚明[7]先使用改进的遗传算法进行预优化，再综合考虑客户需求和路网变化情况对于预优化结果进行动态调整等。

在求解车辆路径优化模型时算法的不断改进，采用多种启发式算法改进的混合算法是常见的改进思路。如：王勇等[8]提出了一种改进的GA-PSO混合算法，综合了精英保留策略、全局搜索能力较强的遗传算法和收敛速度较快的粒子群算法，针对逆向物流车辆路径问题进行优化；滕钥等[9]为求解危险品运输风险的多车型车辆路径问题，在ε-约束法和禁忌搜索相结合的混合算法中嵌入车型匹配策略，对其它领域的多目标多车型物流配送问题的研究具有一定启发。此外，还有一些学者采用非主流新型算法进行求解。如：王超等[10]提出并设计了回溯搜索优化算法求解VRP问题，在该算法的交叉、变异操作中构造出6种路径间搜索算子和4种路径内搜索算子，以提高算法的局部搜索能力；Mokhtarinejad等[11]提出了一种基于机器学习的启发式方法MLBM，通过双聚类方法将客户、制造商和交叉对接中心的位置进行分组。

综上所述，学者们对于VRP问题的研究或深究其中一方面、或适当综合考虑多个条件，将会有更贴近现实情况、求解更精确的算法出现。因此，本文进一步综合考虑动态需求(包括实时路况优化、碳排放量、时间窗等因素)，并且运用改进的遗传算法对模型进行求解，以期对未来的研究提供一定参考价值。

1 问题描述与模型建立

1.1 问题描述

原本的VRP问题是已知一些基本条件(如：多个配送中心和多个顾客的地理位置、顾客对于产品的需求量等)和约束条件(时间窗限制、运输车辆载重量限制)的情况下设计车辆路线，使得货物有序地从多个配送中心到达多个客户，满足优化的目标条件；而DVRPTW是VRP问题的一个分支，是指在原有基础车辆路径优化问题的基础上，考虑客户的动态需求以及时间窗，如图1所示。本文研究的DVRPTW是考虑配送过程中，客户的配送需求是动态变化的。例如：临时取消原有订单、重新产生新订单、数量变更等，需要对原配送路径进行实时重新规划，最终仍然收敛于一个最优路径结果。

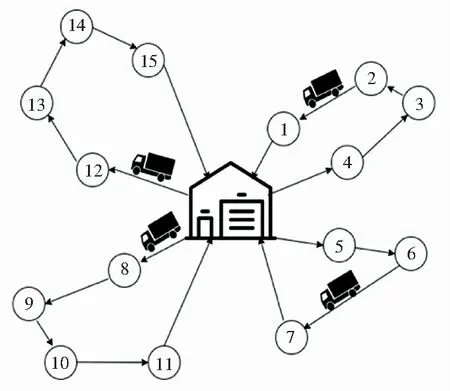
图1 VRP问题图示

配送中心车辆的一天工作路网可以体现在一张完备有向图G(V,E)中，其中V代表所有配送节点，E表示所有边，0是配送中心。有M辆车从配送中心出发，有序经过各顾客节点，在执行初始配送方案的过程中，实时接收新的订单动态，并对原有配送路径进行调整，完成对所有客户需求的配送服务之后返回到配送中心。

1.2 模型假设和符号说明

为了简化计算步骤、突出算法原理，使得计算环境更加理想化，对模型作出以下假设：

(1)本文研究的问题是多个配送中心到多个门店的路径优化问题；

(2)冷链配送中心车辆数量充足、车型号相同，能满足对所有门店的配送；

(3)每辆冷藏车均从配送中心出发，沿着一条路线将货物分发到门店，完成配送之后返回配送中心；

(4)冷藏车行驶的公路状况良好，车辆能够匀速行驶；

(5)配送时间内，外界大气温度不随时间而变动，冷链配送车内的温度保持在恒定水平。

模型中出现的各个符号说明解释见表1。

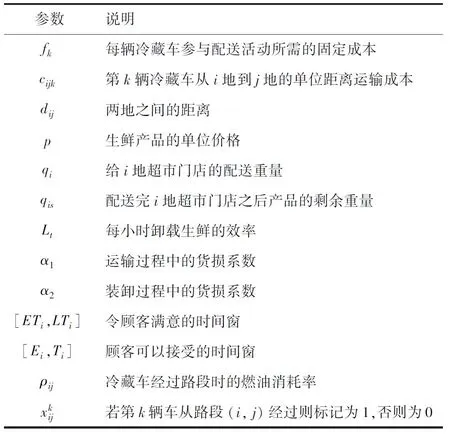
表1 符号说明

1.3 考虑实时路况

车辆在行驶过程中常常受到交通拥堵、各种突发状况等因素的影响，而增加物流配送的成本且影响货物送达时间。因此，在VRP问题的研究中，动态变化是不可忽视的重要因素之一。

研究发现，诱发交通拥堵的原因诸多，通常分为常发性因素和偶然性因素两方面。常发性因素是受固定因素影响，是有规律可循的交通拥堵。如：工作日路况拥堵变化程度较大，潮汐现象更为明显；而休息日人们调整作息时间，早高峰推迟且持续时间增长等。偶然性因素主要是由特殊情况引起。如：受交通事故、大型活动、恶劣天气的影响，造成临时性交通流的集中，导致路段偶发拥堵或者拥堵程度加剧。

本文通过高德地图软件所提供的城市道路实时路况免费接口，可实时获取各路段(i,j)的交通拥堵系数rij，以期在对不同拥堵程度路况赋值的基础上进行计算，量化判断路况随时间的变化情况。配送车辆在路段(i,j)的通行时间为

(1)

式中:dij表示i地与j地的距离，v0是配送车辆正常行驶的平均速度。

1.4 考虑碳中和背景

当前碳中和成为各大研究领域的热点问题，在VRP问题中很多在目标函数中考虑到了碳排放成本，关键在于车辆碳排放量如何测度。常见思路是使用碳税税率计算碳税，直接计入成本。但本文认为，简单地将碳排放转化为经济成本明显忽略了碳排放量最小化的目标，并且现实中车辆行驶过程中的碳排放量会受到包括载重、速度、距离等多种因素在内的影响，计算较为复杂。因此，本文在此处引入一个燃料消耗最优模型并举例验证了其有效性。

本文采用燃油消耗模型来刻画燃油消耗量，即：

(2)

其中，ρ0和ρ*分别为车辆空载和车辆满载时的燃油消耗率；Q是车辆的最大装载量；ρ(Qk)是指当车辆装载量为Qk时的单位行驶里程的燃油消耗量。

为了更加直观地解释燃油消耗量与车辆装载量的关系，假设ρ0=10、Q=400，分别画出当ρ*=20、25、30时的函数图像，如图2所示。

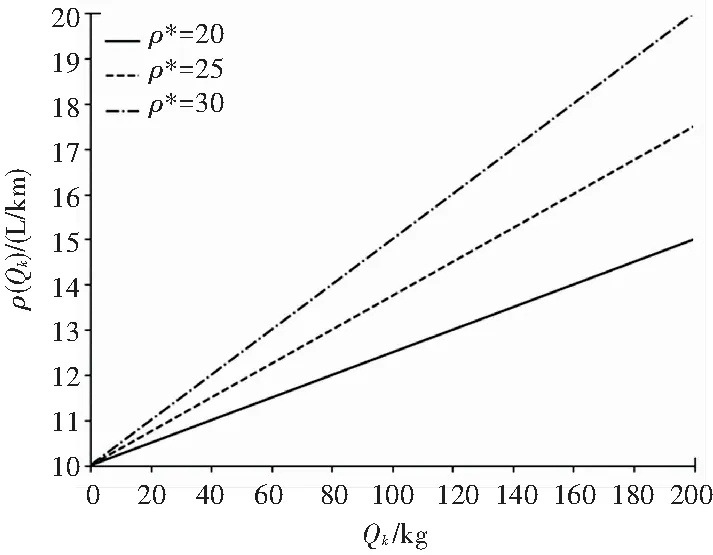
图2 燃油消耗量与车辆装载量关系图

由图2可知，燃油消耗率和车辆装载量呈现正比关系，即车辆装载量越大，燃油消耗量越大，且车辆满载时的燃油消耗率ρ*越大，行驶相同路径所消耗的燃油量就越大。因此，对于任意配送路径段(i,j)，燃油消耗成本为

(3)

其中，c0表示单位燃料成本，dij表示客户点之间的欧式距离。

由此得到车辆在配送时的燃料消耗成本则为

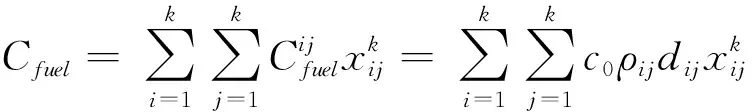
(4)

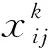
由于ρij受到装载量序列的影响，可以通过设计合理的配送路线，从而达到既减少燃油消耗量、响应国家碳中和政策，又节约了配送成本的目标。

1.5 考虑软时间窗

现如今各大生鲜电商在“前置仓”的模式下纷纷推出 “一小时达”等业务，同时制定了承诺送达机制。如果晚于规定时间送达，则会支付一定的惩罚费用。这表明电商进阶的新门槛在于争分夺秒的时间战，因此本文考虑时间窗，将时间窗作为约束条件之一。

通常情况下，客户对于生鲜农产品的满意程度与产品的新鲜程度相关，而产品的新鲜程度则与生鲜农产品在运输途中花费的时间有关。如果配送商在规定时间内将产品送到，顾客的满意度最高，否则就会降低。具体情况如图3所示。

由图3可知，在配送时间早于或者晚于送达配送门店的顾客满意度值为0，在时间段[Ei,ETi]中，顾客满意度逐渐提高，在[ETi,LTi]中顾客满意度达到最高水平，值为1，而后在[LTi,Li]时间段中，顾客的满意度又逐渐下降趋于0。

图3 客户满意度变化规律图示

为了方便计算，量化顾客满意度，使得满意度与时间呈线性相关关系，定义顾客满意度函数如下：

(5)

其中，[ETi,LTi]是指令顾客满意的时间窗，[Ei,Li]指的是顾客可以接受的时间窗。

1.6 模型建立

基于上述对影响配送成本因素的分析，构建生鲜配送成本函数模型。

目标函数：

(6)

约束条件：

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

其中，目标函数是生鲜冷链配送全程成本的最小化，其中包括固定成本、变动成本、货损成本、惩罚成本和碳排放成本。

约束条件中，式(7)指每辆冷链配送车的载重量不超过额定载重量；式(8)指配送中心进行配送服务的车辆总数不超过配送中心所拥有的车辆数；式(9)、式(10)指每个超市门店只由一辆冷链配送车对其进行服务，并且只服务一次；式(11)指每辆冷链配送车从配送中心出发到超市门店完成配送任务之后必须返回到配送中心；式(12)指硬时间窗约束，必须在规定时间内到达；式(13)、式(14)是指配送变量的0～1约束；式(15)是客户满意度约束。

2 算法设计及实现

本文选用遗传算法对该模型进行求解，并针对遗传算法的一些缺点进行了相应的改进。具体操作包括在选择算子中引入欧式距离、交叉算子时引入自适应交叉算子等，以期增强局部搜索能力、提高解集质量。

2.1 算法原理步骤

遗传算法的主体部分包括选择、交叉和变异算子，改进后的遗传算法流程如图4所示，其主要实现步骤如下：

(1)对染色体进行编码，并且确定初始种群；

(2)对初始种群进行选择、自适应交叉、自适应变异运算；

(3)如果进化代数达到最大，则算法停止并输出解，流程结束；否则返回到自适应交叉算子。

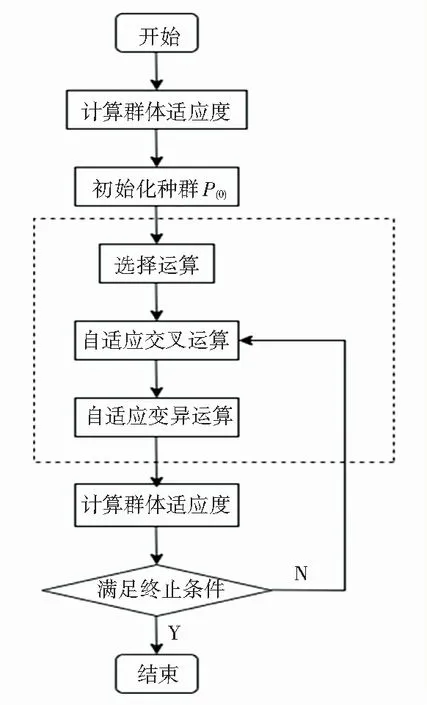
图4 改进的遗传算法流程图

2.2 编码及算子设计

2.2.1 整数编码

在对优化模型采用改进的遗传算法进行求解时，需要先通过一定的编码方式将问题的解集合转化成按照一定次序排列的基因串结构组成的解集合。考虑到二进制编码的一些缺点(如染色体较长时使得算法搜索范围迅速膨胀等)，本文采用自然编码方法对染色体进行编码。

2.2.2 选择算子

选择运算就是在对染色体适应度大小进行评估之后，根据特定方法从父代种群中选择适应度值高的遗传到下一代种群。常见的选择方法包括赌轮选择方法、排挤方法等。本文引入欧式距离，对选择操作进行改进为

(16)

其中，ηi是个体η的第i个基因；θi是个体θ的第i个基因；n是基因个数。

若欧式距离越大，则表明两个个体之间的相似度越小。选择操作步骤如下：

(1)计算种群平均适应度值及每个个体的适应度值，纪录最高适应度值个体；

(2)逐个判断种群个体的适应度值是否小于平均值，若小于，则转到步骤(3)，否则保存个体，直至整个种群判断完成；

(3)随机产生个体，分别计算这个个体的适应度值与原种群中最高适应度值个体之间的欧式距离，选择适应度值与欧式距离之和最大的个体作为新的个体，取代种群中原有个体。

2.2.3 交叉算子

交叉操作是用自适应较差概率，根据当代种群中的最大适应度值fitmax和平均适应度值fitavg对交叉概率Pc进行自适应调整:

其中，fit是进行交叉运算的两个染色体中适应度较高的，Pc1的取值在0.6～1之间。

交叉运算过程如图5所示，其具体步骤如下：

(1)根据公式选择将要进行交叉运算的染色体FA和FB；

(2)在冷链配送车形成的子路径中随机选择两个交叉基因段；

(3)将父代FA中的基因段置于FB基因段前，形成子代；

(4)删去子代中的重复基因点，并更新零点；

(5)形成新的子代FA’和FB’。

图5 交叉算子运算原理图示

2.2.4 变异算子

变异运算是模拟基因突变的过程，其本质就是对多目标优化问题的可行解路径进行局部交换，从而使局部搜索优化能力得到增强。本文依然采用自适应调整概率的方法进行，即:

其中，fit′是指被随机选中进行变异运算的基因。由于基因突变现象在自然界中属于小概率事件，因此Pm1的取值在0.001～0.1之间。

具体操作过程：先计算出变异概率Pm；然后根据Pm选中子代染色体上几个位置的等位基因；随机交换这些位置的基因节点。

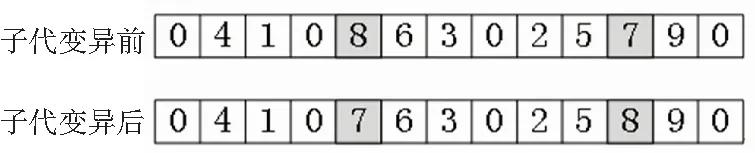
图6 变异算子运算原理图示

3 实例验证

3.1 算例描述及参数设定

某零售企业在城市内有3家配送中心，为该市范围内的客户提供配送服务。配送前一天企业收到了100个客户的配送订单，这些客户分布在城市的不同位置，而且每个客户的货物需求量和要求进行配送的时间窗不同，具体信息见表2、表3。

表2 配送中心信息表

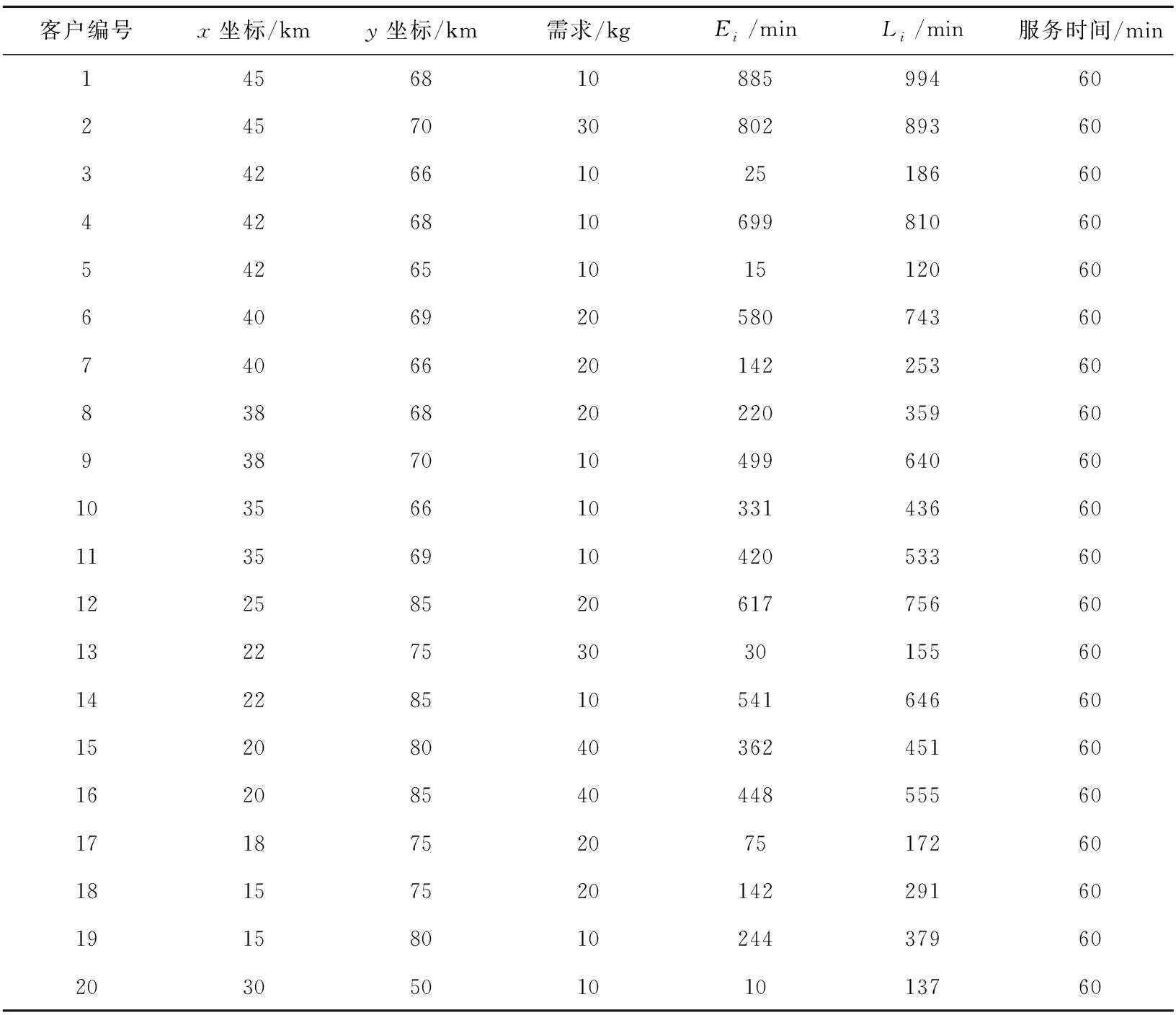
表3 部分客户信息表

另外，对模型中其余参数的设定，见表4。

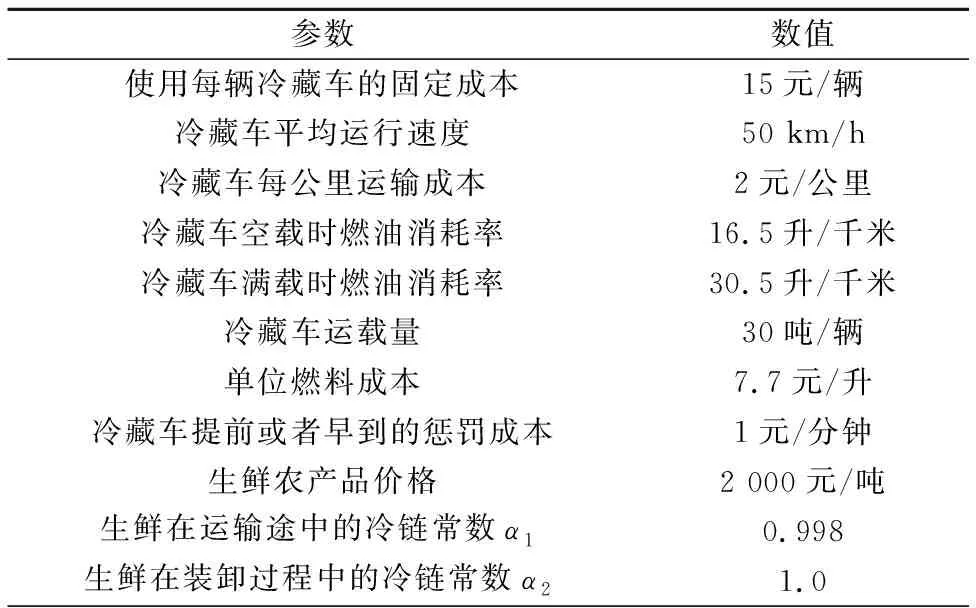
表4 算例参数设计

3.2 实验结果与分析

本文算例中所用的改进遗传算法参数设置包括：种群规模100个，最大迭代次数500，竞赛规模50个，交叉概率0.8，变异概率0.1。使用Python3.9.5编程；运行程序的计算机CPU型号为Apple M1，内存16 GB。

改进算法求解结果如图7、图8所示。此外，为了验证算法的有效性，将改进的算法结果与原遗传算法(图9)进行比较。其结果显示，未改进的遗传算法收敛速度较慢，且目标函数成本较高。

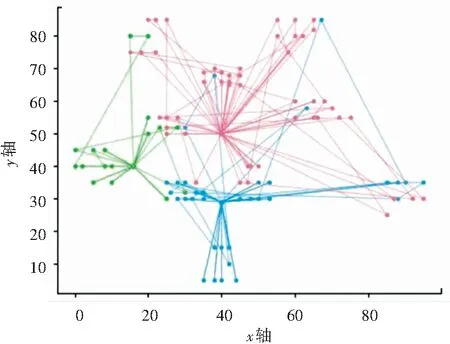
图7 改进的遗传算法路径优化结果图

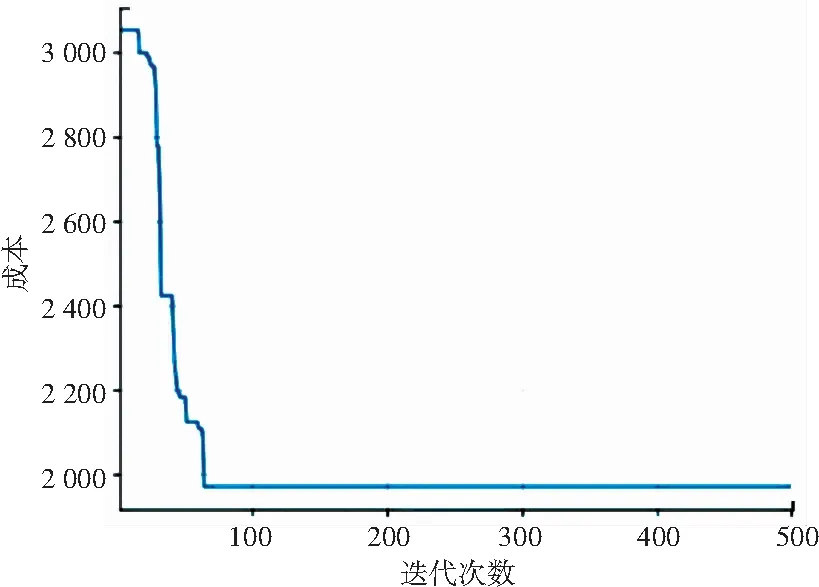
图8 改进的遗传算法迭代结果图

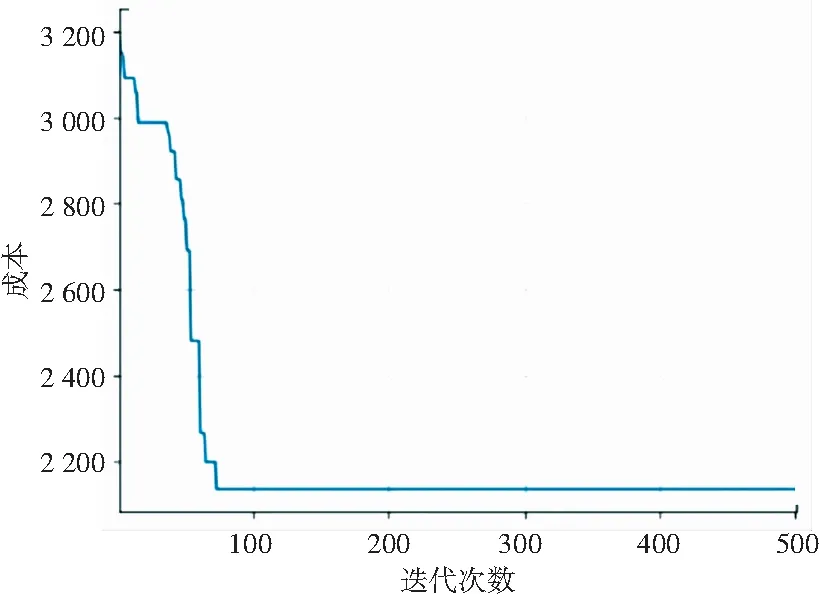
图9 未改进的遗传算法迭代结果图

由表5可知，若使用改进遗传算法求解得出成本为1 969元，而未经改进的遗传算法求解得出的成本约为2 134元，经改进成本降低约7.73%，对于降低配送总成本有一定的效果。如果将其方法应用于大规模大范围的路径优化，则经济效益将更为突出。

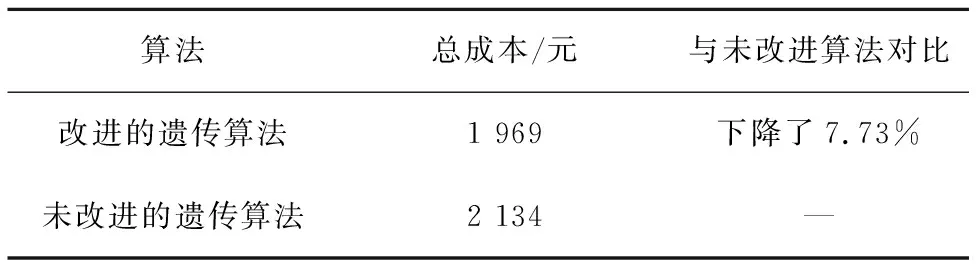
表5 算法结果对比

4 结束语

本文在疫情期间生鲜电商线上需求量剧增的背景下，针对多配送站的车辆路径优化问题，考虑了包括实时路况、碳排放、时间窗等因素在内的动态因素，并将其转化为静态车辆路径问题进行求解。建立了以求最小总配送成本和最大客户满意度的多目标优化模型，并采用改进的遗传算法求解，最后通过案例进行了仿真实验。实验结果表明：改进的遗传算法比未改进的遗传算法成本提高了7.73%。因此，在动态车辆路径问题中使用本文提出的改进算法，能够有效降低配送成本，更加具有现实意义。在后续的研究中，可将动态需求的考虑转化为静态需求，转而分解为两阶段方法。