含ISOP-DAB变换器的中低压直流配电系统阻抗建模及稳定性分析

刘英培，杨博超，石金鹏，朱宇琦

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

随着我国“双碳”目标的提出，可再生能源的开发和利用得到了大力发展，但电力负荷的快速增长、可再生能源渗透率升高使得传统交流配电网的拓扑结构和配电方式已经不能满足现有用户的需求。而“十四五”作为碳达峰的关键期，直流配电网以其传输效率高、电能质量高、控制灵活性强等优势将成为未来以可再生能源为主体的新型电力系统的重要组成部分［1-2］。

与此同时，高比例可再生能源和高比例电力电子设备（简称“双高”）已成为直流配电系统的主要特征，并且系统内缺少类似于传统同步发电机的强自然惯量支撑单元，使得整个系统因其低惯量、弱阻尼的特性所引起的稳定性问题尤为突出［3-4］；高比例电力电子设备虽然可以实现直流配电系统的快速响应和控制，但也使得系统更容易受到各种扰动的影响，且不同类型变换器及其控制方式均对系统小干扰稳定性有不同程度的影响［5］。因此，直流配电网小干扰稳定性问题受到了国内外学者的广泛关注。

目前，直流配电网小干扰稳定性研究主要集中于单一母线的直流系统［6］，文献［7］以基于下垂控制的直流微电网为研究对象推导了系统的小信号模型，通过特征值分析研究了负荷类型、下垂系数等参数变化对系统稳定性的影响。文献［8］通过建立三端直流配电系统的戴维南等效模型，利用奈奎斯特判据对比分析了系统参数变化对采用主从控制和下垂控制的直流系统稳定性的影响。文献［9］通过构建中压直流配电网的等效阻抗模型分析了储能单元与直流母线间的双向交互对系统稳定性的影响。文献［10］从阻抗角度分析了Boost变换器与电压源换流器（voltage source converter，VSC）电压源之间的交互特性，发现LC滤波器会引起系统直流电压在输出阻抗谐振频率点附近的振荡。

相比于单母线直流系统，中低压直流配电系统含有多个电压等级，其复杂的拓扑结构使得传统的阻抗判据无法直接分析系统的稳定性，并且中低压直流配电系统具有更明显的“双高”特征，进而导致基于状态空间的特征值分析法出现维数灾问题［11］。为研究中低压直流配电系统的稳定性，文献［12］忽略了交流微电网中平衡单元以及互联装置AC-DC的内环控制，并采用模块化建模建立了交直流混合微电网在不同运行模式下的小信号模型，利用根轨迹法研究了控制器参数对系统稳定性的影响。文献［13-14］通过构建整个多电压等级直流系统的小信号模型发现不同变量之间的传递函数具有相同的等效环路增益，由此，在保证系统内所有单元均能单独稳定运行的前提下该等效环路增益可用来分析系统的稳定性，但其推导过程相对比较繁琐，并且不易推广到更复杂的场景中。文献［15］针对多电压等级直流系统，以互联变换器（interlinking converter，IC）的高压侧端口或低压侧端口作为分界线将整个系统划分为2个子系统，进而通过求解子系统的等效阻抗并利用奈奎斯特判据评估系统的稳定性，虽然其推导过程较等效环路增益更简洁明了，但并未体现出明确的源荷分界点。

综上所述，针对中低压直流配电系统稳定性问题的研究相对较少，现有的稳定性分析方法仍具有一定的局限性。为此，本文首先针对含输入串联输出并联型双有源桥（input series output parallel-dual active bridge，ISOP-DAB）变换器的中低压直流配电系统建立了ISOP-DAB变换器的二端口阻抗模型以及其他单元的阻抗模型。然后，提出了一种适用于中低压直流配电系统的稳定性分析方法。该方法依据系统内各单元的端口特性将其进行分类，并根据IC的二端口阻抗模型分别得到中低压直流配电系统在中、低压侧的等效阻抗模型，在此基础上推导出相应母线侧的等效阻抗比，以此来判断系统的稳定性。最后，基于PSCAD／EMTDC平台搭建上述系统的时域仿真模型，通过理论计算以及仿真实验分析系统参数对稳定性的影响。仿真结果验证了ISOP-DAB变换器的二端口阻抗模型以及所提稳定性分析方法的正确性以及有效性。

1 含ISOP-DAB变换器的中低压直流配电系统各单元的数学模型

1.1 含ISOP-DAB变换器的中低压直流配电系统结构

基于深圳电网柔性中压直流配电示范工程［16］，含ISOP-DAB变换器的中低压（medium voltage and low voltage，MV／LV）直流配电系统如图1所示。中压直流母线采用“手拉手”结构经过VSC接入交流电网，集成了直流变压器和恒功率负载。为满足大功率传输，IC采用ISOP-DAB变换器实现功率双向传输。低压直流母线通过ISOP-DAB变换器与中压直流母线互联，集成了光伏发电单元、储能单元和恒功率负载。其中，光伏发电单元采用Boost变换器通过最大功率点追踪（maximum power point tracking，MPPT）控制实现最大功率输出。储能单元采用双向Boost变换器与ISOP-DAB变换器共同维持直流母线电压稳定。

为得到含ISOP-DAB变换器的中低压直流配电系统的等效模型，下文将分别建立系统中ISOP-DAB变换器、VSC子系统、光伏单元、储能单元、恒功率负载单元的小信号模型。

1.2 ISOP-DAB变换器数学模型

ISOP-DAB变换器的主电路结构如图2所示。图中：uin_DAB、iin_DAB和uo_DAB、io_DAB分别为变换器输入侧和输出侧的电压、电流；Lsi(i=1，2，…，k)为第i个双有源桥（DAB）子模块的辅助电感；高频变压器变比为Ni∶1；C1i、C2i分别为第i个DAB子模块的输入、输出侧电容；uini为第i个DAB子模块的输入电压；i1i、i2i分别为第i个DAB子模块的输入、输出电流。

图2 ISOP-DAB变换器的主电路结构Fig.2 Main circuit structure of ISOP-DAB converter

ISOP-DAB变换器作为中低压直流母线间互联装置，可以将其等效为二端口网络以反映中低压母线电压之间的耦合关系［17］，定义中压侧为输入端，低压侧为输出端。在直流配电系统并网运行时，ISOPDAB变换器的控制目标一般为实现低压直流母线电压稳定控制，因此，其闭环二端口阻抗模型如式（1）所示。

式中：Δ表示对应变量的小信号分量，后同；YMDAB为中压侧闭环输入导纳；GMDAB为闭环反向电流增益；GLDAB为闭环电压增益；ZLDAB为低压侧闭环输出阻抗。

根据图2，整个ISOP-DAB变换器的小信号模型可以由单个DAB子模块的小信号模型根据输入串联输出并联的特点推广得到。第i个DAB子模块的开环小信号模型已在文献［9］中给出，具体为：

式中：di为第i个DAB的移相比；fs为开关频率。

由式（2）及图2可以得到ISOP-DAB变换器的小信号模型如附录A图A1所示，其对应的ISOP-DAB变换器的开环线性化方程为：

本文假设每个DAB子模块具有相同的变压器匝数比NDAB、辅助电感Ls、输入电容C1和输出电容C2，并且每个模块在稳态工作点具有相同的移相比D。令G1d=G1d1=G1d2=…=G1dk，G12=G121=G122=…=G12k，G2d=G2d1=G2d2=…=G2dk，G21=G211=G212=…=G21k，则式（4）可化简为：

ISOP-DAB变换器的具体控制结构见附录A图A2，其采用单移相调制，为实现模块间功率平衡以及各模块间的解耦控制，控制部分采用双环解耦控制策略，由输入均压环和输出电压环组成。其中，输出电压环采用下垂控制；输入均压环采用解耦控制策略，即将前k-1个子模块的均压环输出相加作为第k个子模块的校正信号。

由图A2可得k个子模块的总移相比的小信号分量ΔdDAB为：

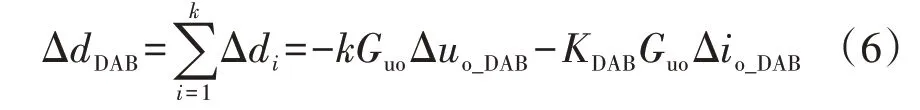
式中：Guo为输出电压环PI控制器的传递函数；KDAB为DAB下垂控制的下垂系数。

联立式（5）和式（6）可得ISOP-DAB变换器的闭环二端口网络矩阵中各元素为：

考虑到ISOP-DAB变换器两侧的直流线路对其阻抗模型的影响，需要对式（7）各元素进行修正，修正过程如下。

直流线路采用π型等值模型，由于其两侧分布电容较小，因此可以将两侧电容整合到变换器接口的电容中［8］。忽略两侧分布电容，直流线路等效阻抗Zline为：

式中：Rline、Lline分别为直流线路等效电阻和电感。

由式（1）及式（8）可得计及直流线路的ISOPDAB变换器二端口阻抗模型如附录A图A3所示。因此可推导得到修正后的ISOP-DAB变换器的闭环二端口阻抗模型为：

式中：iin_IC、io_IC分别为计及直流线路后ISOP-DAB变换器的输入、输出侧电流；uMBUS、uLBUS分别为中压和低压直流母线电压；ZlineM、ZlineL分别为ISOP-DAB变换器输入侧和输出侧的线路等效阻抗。

中低压直流配电系统中的VSC换流器系统、储能单元、光伏单元和恒功率负载的数学模型详见附录B。

2 中低压直流配电系统稳定性分析方法

2.1 中低压直流配电系统小信号模型

直流配电系统中的发电单元和负载单元可以按照其变换器在母线侧端口的输入／输出特性重新进行划分［18-19］：将控制或影响母线侧电压的单元称为广义电压源（generalized voltage source，GVS）；将控制或影响母线侧端口电流的单元称为广义电流源（generalized current source，GCS）。中低压直流配电系统中，GVS主要包括运行在电压支撑模式下的VSC系统和发电单元；GCS主要包括各种负载单元以及运行在功率模式下的VSC系统和发电单元。根据以上分类，由图1可得到含ISOP-DAB变换器的中低压直流配电系统的等效模型如图3所示。为更具一般性，采用IC代替ISOP-DAB变换器，系统中压直流母线侧共含有M1个GVS子系统和M2个GCS子系统，低压直流母线侧共含有M3个GVS子系统和M4个GCS子系统。图中：iMov_m、iMoc_n分别为中压侧第m个GVS的输出电流、第n个GCS的输入电流；iLov_p、iLoc_q分别为低压侧第p个GVS的输出电流、第q个GCS的输入电流。

图3 中低压直流配电系统等效模型Fig.3 Equivalent model of MV／LV DC power distribution system

进一步地，GVS的小信号模型可以等效为理想电压源串联输出阻抗的形式，GCS的小信号模型可以等效为理想电流源并联输入阻抗的形式。据此并由式（9）可以得到中低压直流配电系统的等效小信号模型如附录C图C1所示。

2.2 系统中低压侧等效阻抗比

由图C1可以得到中、低压子系统中的电流关系分别如式（11）、（12）所示。

联立式（9）和式（12）并结合图C1可推导得到IC及低压子系统的等效输入阻抗Zin_LS为：

式中：uLv_p、ZLv_p分别为低压侧第p个GVS的等效理想电压源、输出阻抗；iLc_q、ZLc_q分别为低压侧第q个GCS的等效理想电流源、输入阻抗；ZLV为低压子系统中所有GVS的等效输出阻抗；ZLC为低压子系统中所有GCS的等效输入阻抗。

由式（13）并利用诺顿等效定理，可将IC及其所连接的低压子系统等效为理想电流源ΔiLS并联等效输入阻抗Zin_LS的形式。据此，中低压直流配电系统在中压母线侧的等效阻抗模型如附录C图C2所示。

类似地，可以推导得到IC及中压侧子系统的等效输出阻抗Zo_MS为：

式中：uMv_m、ZMv_m分别为中压侧第m个GVS的等效理想电压源、输出阻抗；iMc_n、ZMc_n分别为中压侧第n个GCS的等效理想电流源、输入阻抗；ZMV为中压子系统中所有GVS的等效输出阻抗；ZMC为中压子系统中所有GCS的等效输入阻抗。

由式（15）并利用戴维南等效，IC及其所连接的中压子系统可以等效为理想电压源ΔuMS串联等效输出阻抗Zo_MS的形式。中低压直流配电系统在低压母线侧的等效阻抗模型见附录C图C3。

由图C2、C3以及阻抗匹配准则可得到中低压直流配电系统在中压侧的等效阻抗比TmM和低压侧的等效阻抗比TmL分别为：

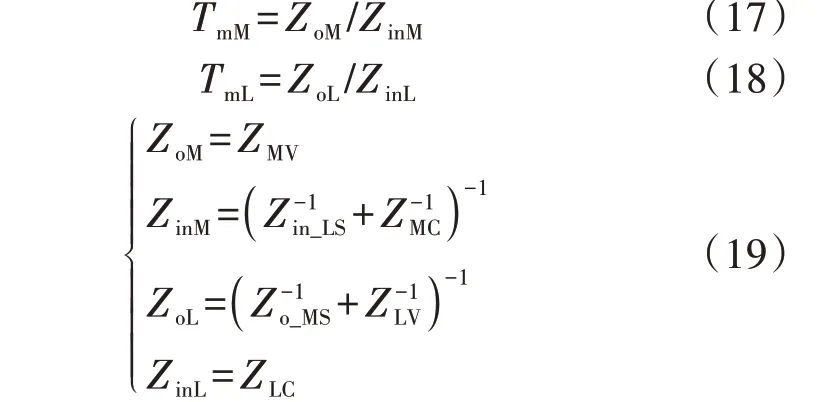
由式（17）、（18）可推导得到1/( 1 +TmM)、1/( 1 +TmL)的表达式，分别如附录C式（C1）、（C2）所示。通过对比发现，1/( 1+TmM)、1/( 1 +TmL)分母相同，即二者具有相同的极点。因此，当TmM或TmL满足奈奎斯特判据时，可保证中低压直流配电系统稳定运行，换言之，令ω从0变化至+∞，若TmM或TmL的奈奎斯特曲线从左侧绕过点（-1，0）的次数N与其右半平面极点数P满足P=2N，则1/( 1 +TmM)、1/( 1 +TmL)无右半平面极点，中低压直流配电系统可稳定运行，否则不稳定。

由上述分析可知，中低压直流配电系统可以简化为2个单母线直流子系统，且任一子系统稳定都可以保证整个直流配电系统的稳定性。由此可见，利用本文所提稳定性分析方法可以将含直流微电网群的多电压等级直流配电系统简化为多个共母线直流系统，进而评估系统的小扰动稳定性。

3 含ISOP-DAB变换器的中低压直流配电系统稳定性分析及仿真验证

为验证本文所提稳定性分析方法的有效性并分析系统参数对稳定性的影响，首先需要根据系统内各单元变换器以及ISOP-DAB变换器的输入、输出特性分别得到两端中低压直流配电系统在中压母线侧和低压母线侧的等效阻抗模型，如图4所示。图中：uVSC1、uVSC2分别为换流器系统VSC1、VSC2等效电压源输出电压；ZVSC1、ZVSC2分别为换流器系统VSC1、VSC2的输出阻抗；uB为储能单元等效电压源输出电压；ZB为低压侧储能单元输出阻抗；iPV为光伏单元等效电流源输出电流；ZPV为低压侧光伏单元输出阻抗；uMS为中压侧子系统等效电压源输出电压；iLS为低压侧子系统等效电流源输出电流；ZCPLM、ZCPLL分别为中、低压侧恒功率负载的输入阻抗。

图4 直流系统中、低压侧等效阻抗模型Fig.4 DC system equivalent impedance model at MV and LV side

由式（13）、式（15）及图4可以得到中低压母线侧的输入、输出阻抗为：

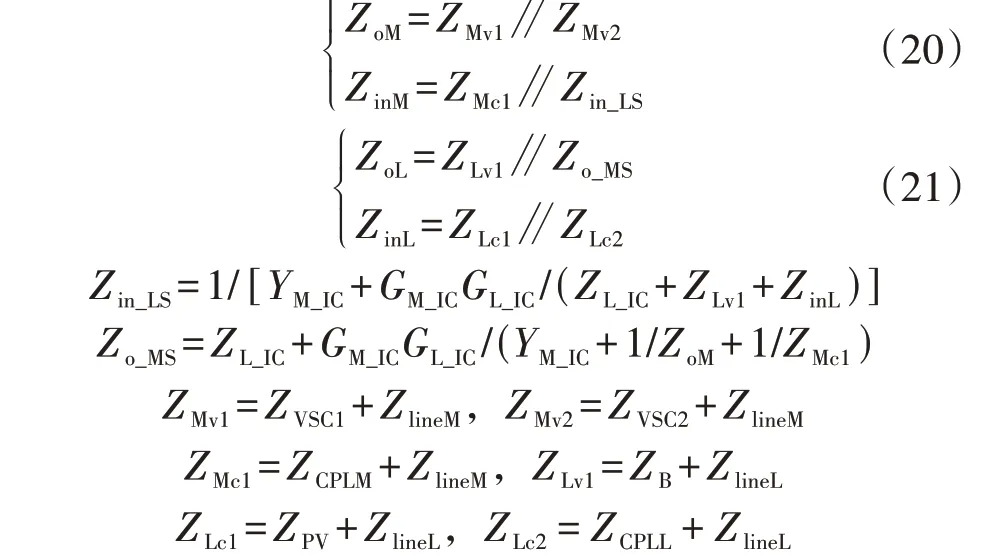
由式（17）、（18）、（20）、（21）可得系统在中低压两侧的阻抗比为：

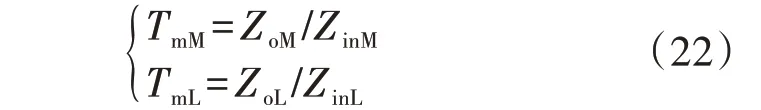
3.1 中低压子系统等效阻抗模型扫频验证

为验证ISOP-DAB变换器二端口阻抗模型及中低压子系统等效模型的准确性，基于PSCAD／EMTDC仿真平台搭建图1所示的含ISOP-DAB变换器的中低压直流配电系统，系统中VSC及其所连交流系统、ISOP-DAB变换器、恒功率负载、光伏发电单元、储能单元以及中低压侧直流π型线路参数见附录D表D1—D3。

工况1：VSC1、VSC2给定电压为10 kV，VSC1采用定直流电压控制，VSC2采用下垂控制，下垂系数取0.02，中压侧恒功率负载功率设置为10 MW，ISOPDAB变换器及储能单元给定电压为800 V，光伏单元输出功率为100 kW，低压侧恒功率负载功率设置为0.4 MW。

本文在工况1下采用附录D图D1所示的方法分别将ISOP-DAB变换器的输入及输出侧串联交流电压源作为扰动信号，通过改变电压源的给定频率（1～10 kHz），测量不同频率下直流电压扰动量Δuin(Δuo)与直流电流扰动量Δiin(Δio)的比值，该比值即为等效阻抗测量值。为精确测量，交流小信号电压源的幅值取相应直流母线额定电压的5 %［20］。等效阻抗实测值与理论值的对比结果如图5所示。

图5 等效阻抗扫频验证结果Fig.5 Results of equivalent impedance sweep frequency verification

根据图5可知，中、低压直流子系统的等效阻抗模型均与其仿真实测模型在1～10 kHz频段基本吻合，可以进行稳定性分析。

3.2 中压侧参数对稳定性的影响

首先利用式（22）分析中压母线侧的恒功率负载功率以及线路参数的变化对中低压直流配电系统稳定性的影响。

3.2.1 中压侧恒功率负载功率的影响

为研究中压侧恒功率负载功率变化对系统稳定性的影响，在工况1下设置中压侧恒功率负载从10 MW变化至25 MW，其他参数保持不变。当ω从0变化至+∞时，TmM的奈奎斯特曲线及其极点分布如附录E图E1所示。由图可见，随着中压侧恒功率负载功率的增加，中低压直流配电系统的稳定性逐渐下降，当负载功率达到25 MW时，TmM的奈奎斯特曲线沿顺时针方向从点（-1，0）的左侧绕过且TmM无右半平面极点，系统失稳。

当中压侧负载功率为25 MW时，系统在中压母线侧的输入阻抗ZinM及输出阻抗ZoM的Bode图如图6所示。由图可知，ZinM和ZoM的幅频响应在269 Hz处相交，此时相频响应曲线相差181.5°＞180°。因此，系统在负载功率为25 MW时失稳，且振荡频率为269 Hz。

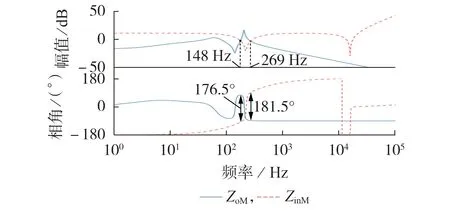
图6 中压侧等效输入、输出阻抗Bode图Fig.6 Bode graph of equivalent input and output impedances at MV side

为进一步验证所提方法的有效性，基于工况1在PSCAD仿真模型中设置中压侧恒功率负载功率在2 s时由15 MW增加至20 MW，3 s时增至25 MW。系统中低压侧母线电压波形如图7所示。由图可知，当中压侧恒功率负载达到25 MW时，系统失稳，与图E1中分析结果一致。

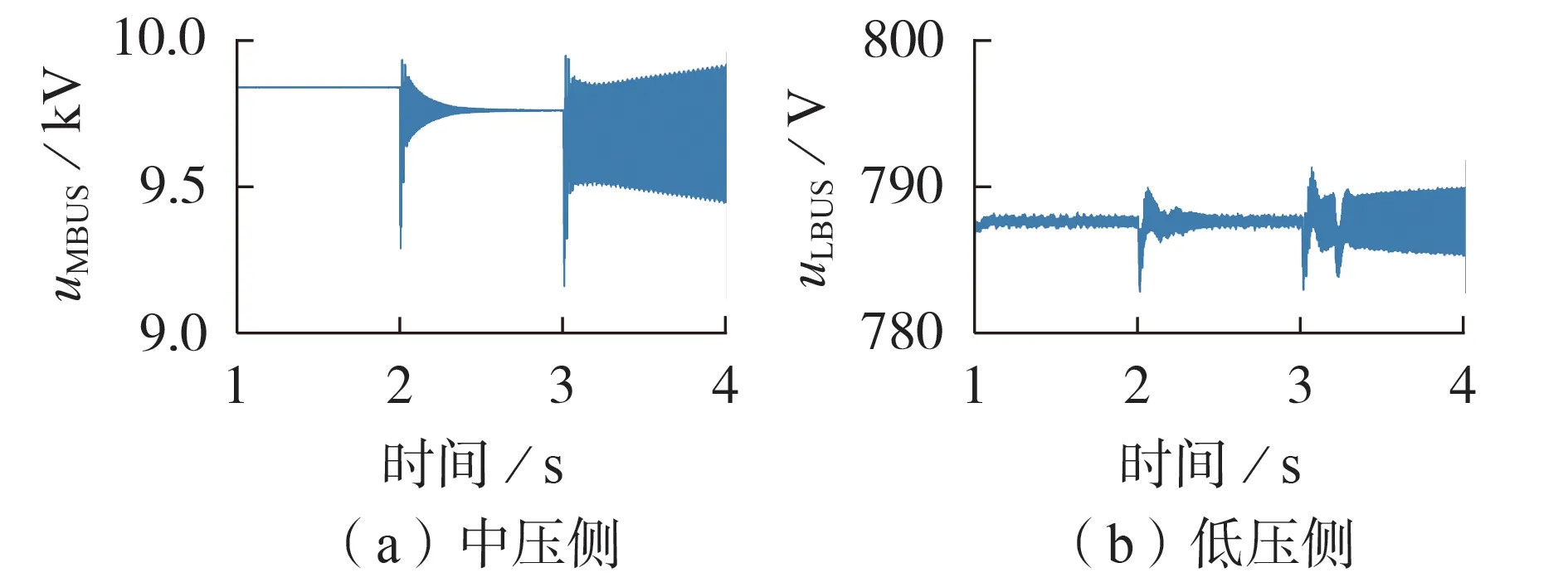
图7 中压侧恒功率负载变化时的中、低压侧母线电压Fig.7 DC bus voltage at MV and LV side when constant power load at MV side changes

对失稳后中压侧母线电压波形进行快速傅里叶变换（fast Fourier transform，FFT）分析，分析结果见附录E图E2。由图可知，电压振荡频率约为267 Hz，与图6中的理论分析结果一致。

系统低压侧等效阻抗比TmL的奈奎斯特曲线及其极点分布如附录E图E3所示。当中压侧恒功率负载变化时，低压侧子系统各单元稳态工作点并无明显变化，因此中压侧负载单元功率增大仅影响TmL的极点分布，而对TmL的奈奎斯特曲线影响不大。当中压侧负载功率达到25 MW时，TmL的奈奎斯特曲线虽然没有从点（-1，0）左侧绕过，但此时TmL存在右半平面的极点，未满足奈奎斯特判据，系统失去稳定性，与中压侧阻抗比判据判断的结果一致。

因此，为分析简便，下文将采用中压侧等效阻抗比TmM分析系统中压母线侧参数变化时对系统稳定性的影响。

3.2.2 中压侧线路参数的影响

为研究中压侧线路参数变化对系统稳定性的影响，在工况1下设置中压侧恒功率负载为20 MW，中压侧线路电感不变，线路电阻由0.2 Ω变化至0.05 Ω。TmM的极点分布及其奈奎斯特曲线如附录E图E4所示。由图可知，随着中压侧线路电阻的减小，系统的稳定性逐渐下降，当线路电阻达到0.05 Ω时，TmM虽无右半平面极点，但其奈奎斯特曲线从点（-1，0）左侧绕过，系统失稳。

同等条件下在PSCAD仿真模型中设置中压侧线路电阻在2 s时由0.1 Ω增加至0.2 Ω，3 s时减小至0.05 Ω。系统中低压侧母线电压波形如图8所示。

图8 中压侧线路电阻变化时中、低压侧母线电压Fig.8 DC bus voltage at MV and LV side when line resistance at MV side changes

由图8可知，当中压侧线路电阻为0.05 Ω时，系统失稳，与图E4中的理论分析结果一致。

同理，基于工况1设置中压侧恒功率负载为20 MW，线路电阻不变，线路电感由0.5 mH变化到2 mH。TmM的奈奎斯特曲线见附录E图E5。由图可见，随着中压侧线路电感的增加，系统的稳定性逐渐下降，当线路电感达到2 mH时，TmM无右半平面极点，其奈奎斯特曲线从点（-1，0）左侧绕过，系统失稳。

同等条件下在PSCAD仿真模型中设置中压侧线路电感在2 s时由1 mH增加至2 mH，3 s时减小至0.5 mH，中低压直流母线电压波形如附录E图E6所示。由图可见，当中压侧线路电感为2 mH时，系统失稳，与附录E图E5中理论分析结果一致。

3.3 低压侧参数对稳定性的影响

采用同样的方法对低压母线侧的恒功率负载功率以及线路参数的变化对中低压直流配电系统稳定性的影响。

工况2：中压侧恒功率负载设置为15 MW，低压侧恒功率负载设置为0.6 MW，其他参数与工况1保持一致。

3.3.1 低压侧恒功率负载功率的影响

为研究低压侧恒功率负载功率变化对系统稳定性的影响，在工况2下设置低压侧恒功率负载从0.4 MW变化到1 MW，其他参数保持不变，TmL的极点分布及奈奎斯特曲线如附录E图E7所示。由图可见，随着低压侧恒功率负载功率的增加，中低压直流配电系统的稳定性逐渐下降，当负载功率达到1 MW时，TmL无右半平面极点，当ω从0变化至+∞时其奈奎斯特曲线沿顺时针方向从点（-1，0）左侧绕过，系统失稳。

当低压侧负载功率为1 MW时，系统在低压母线侧的输入阻抗ZinL及输出阻抗ZoL的Bode图如图9所示。由图可知，ZinL和ZoL的幅频响应在430 Hz处相交，此时相频响应曲线相差184.8°＞180°。因此，系统在负载功率为1 MW时失稳，且振荡频率为430 Hz。

图9 低压侧等效输入、输出阻抗Bode图Fig.9 Bode graph of equivalent input and output impedance at LV side

基于工况2在PSCAD仿真模型中设置低压侧恒功率负载功率在2 s时由0.6 MW增加至0.8 MW，3.5 s时增至1 MW，中低压侧母线电压波形见图10。由图可知，当低压侧恒功率负载达到1 MW时，系统失稳，与附录E图E7中分析结果一致。

图10 低压侧恒功率负载变化时中、低压侧直流母线电压Fig.10 DC bus voltage at MV and LV side when constant power load at LV side changes

对失稳后低压侧母线电压波形进行FFT分析，分析结果见附录E图E8，其中电压振荡频率约为431 Hz，与图9中理论分析一致。

系统中压侧等效阻抗比TmM的奈奎斯特曲线及其极点分布如附录E图E9所示。由于中低压侧容量相差较大，低压侧恒功率负载的变化只影响TmM的极点分布，而对TmM的奈奎斯特曲线影响不大。当低压侧负载功率达到1 MW时，TmM的奈奎斯特曲线并没有绕过点（-1，0），但此时TmM存在右半平面的极点，未满足奈奎斯特判据，系统失去稳定性，与低压侧阻抗比判据判断的结果一致。

因此，下文将采用低压母线侧的阻抗比TmL进行稳定性分析。

3.3.2 低压侧线路参数的影响

为研究中压侧线路参数变化对系统稳定性的影响，在工况2下设置低压侧线路电感保持0.2 mH不变，线路电阻由0.02 Ω变化至0.005 Ω，TmL的极点分布及奈奎斯特曲线见附录E图E10。由图可见，随着低压侧线路电阻的减小，TmL的奈奎斯特曲线向点（-1，0）靠近，中低压直流配电系统的稳定性逐渐下降。

同理，在工况2下设置线路电阻保持0.01 Ω不变，线路电感由0.1 mH变化至0.5 mH，TmL的极点分布及奈奎斯特曲线见附录E图E11。由图可见，低压侧线路电感的增加不利于系统的稳定运行。

4 结论

本文建立了10 kV／800 V含ISOP-DAB变换器的中低压直流配电系统的等效阻抗模型，将多母线的直流系统等效为单一母线系统，提出一种基于阻抗模型的中低压直流配电系统稳定性分析方法，在此基础上分析了恒功率负载及直流线路参数对直流配电系统稳定性的影响，最后在PSCAD／EMTDC平台中验证了ISOP-DAB变换器的二端口阻抗模型与系统等效阻抗模型的准确性以及所提稳定性分析方法的有效性，得到以下结论。

1）依据中低压直流配电系统的阻抗模型可以将其简化为单一母线直流系统，中、低压侧等效阻抗比均能够评估整个系统的稳定性，且二者分析结果一致。

2）分析了中低压侧线路参数和恒功率负载对系统稳定性的影响；根据奈奎斯特曲线对比可知，在本文参数下，直流线路电阻减小和电感增大均会使系统稳定性下降；当中、低压侧恒负载功率增加时，均会导致系统的稳定性下降。

3）当系统因一侧源荷阻抗不匹配失稳时，该侧子系统在另一母线侧的等效输出或输入阻抗会存在右半平面极点，由此可以初步确定系统失稳的原因。

本文所提稳定性分析方法可推广到更复杂的含直流微电网群的多电压等级直流配电系统中。

附录见本刊网络版（http：//www.epae.cn）。