扩展Cox模型在非线性生存资料分析中的预测能力比较

陈雨轩，韦红霞，潘建红，安胜利

1南方医科大学公共卫生学院生物统计学系，广东 广州 510515；2国家药品监督管理局药品审评中心，北京100022

在医学研究中，研究者们经常通过构建回归模型来分析变量间的关系。通常回归模型的使用前提假设是自变量和因变量间或因变量的某种函数间呈线性关联，但在实际应用中这个条件并不一定满足。常见的解决方法是将连续型变量分类，但分类数目和节点位置的选择往往带有主观性，并且分类会损失信息。因此，一个更好的解决方法是拟合自变量与因变量之间的非线性关系。

以往生存分析中对非线性数据的处理通常有两种，一个是直接拟合机器学习模型；另一个就是把连续型的变量转换成分类变量并以哑变量形式纳入传统生存分析模型。但是后者可能导致协变量不满足比例风险假定［1］。为了弥补传统生存分析模型的应用条件限制及缺陷，避免对变量关系间的形状进行参数约束，目前常用平滑工具来解决这类问题。平滑工具中限制性立方样条（RCS）是目前分析非线性关系的最常见的方法之一［2-4］。生存分析中，限制性立方样条结合Cox模型，不仅可以用于探索非线性关系，越来越多的学者也将其运用于构建预测模型［5-8］。

近年来机器学习以及深度学习神经网络的发展，使得更多的方法可以用于解决复杂生存数据构建预测模型。深度学习属于机器学习的一个子域，机器学习方法中，随机生存森林方法是最常见的分析方法，当有新的机器学习方法提出时一般会跟随机生存森林做比较，所以本文也考虑纳入随机生存森林作为参照方法。机器学习生存分析方法，包括随机生存森林、条件推断森林等［9-13］；深度学习神经网络方法如DeepSurv，DeepHit，Neural net-extended time-dependent cox model等［14］，都可以解决非线性、交互等复杂情况，其在高维数据中有明显的优势，并且不需要满足传统Cox回归模型比例风险假定等前提条件，但是机器学习以及神经网络模型实施起来较为复杂，特别是深度学习神经网络需要用Python软件来实现，其所花费的时间比传统模型要多。直接使用机器学习或者深度学习方法来分析，花费人力物力的同时其拟合效果也不一定比传统生存分析方法好。所以在非线性关系存在的生存数据分析中，各方法的优劣还有待研究比较。

1 方法

方法部分主要介绍Cox比例风险回归模型（Cox）、限制性立方样条Cox回归（Cox_RCS）、深度生存神经网络（Cox_DNN）这3种方法。

1.1 Cox比例风险回归模型

Cox比例风险回归模型是1972年由英国统计学家D.R.Cox提出的一种半参数模型［15］，其数学公式为：

其中λ(t,Xi)为受试者在一组预测变量Xi条件下所预测的t时刻的事件发生风险，λ0(t)是基线风险函数，β为预测变量的回归系数。医学研究人员常使用Cox模型评估预后协变量在死亡或疾病复发等事件中的重要性，并随后告知患者其治疗选择；Cox 比例风险回归模型使用时需要满足两个基本假定：（1）比例风险假定：λ(t,Xi)/λ0(t)为固定值，即协变量对生存率的影响不随时间的改变而改变；（2）对数线性假定：对数风险比应与模型中的连续型协变量呈线性关系。模型中的连续型变量可能会对生存时间产生非线性风险，如果不考虑这个风险，可能会导致结果偏差。

1.2 限制性立方样条Cox回归

限制性立方样条是最常用来检验假设关系不是线性的一种方法，或者用来总结非线性关系的一种方法。限制性立方样条函数只是一个自变量的变换。因此，它们不仅可以用于普通最小二乘回归，还可以用于逻辑回归、生存分析等。

临床评估科学研究所进行的两项研究很好地说明了限制性立方样条的两种用途。一是识别非线性关系，二是构建预测模型。如Κendzerka等［5］使用限制性立方样条来检验连续型预测变量与心血管事件相关呼吸暂停患者住院风险之间的线性关系，当发现非线性的关联时，通过RCS构建预测模型实行风险预测。正如前文所述，连续型变量进行分类可能会丢失重要的信息，因此限制性立方样条为分析连续型预测变量对预测结果的影响提供了一个有用的工具，它在预测变量和结局之间的关系形式上允许很大的灵活性。

限制性立方样条Cox 模型，1989 年由Durrleman等［16］学者提出，用于生存分析中拟合灵活的非线性关系。在Cox比例风险回归模型中，考虑变量的非线性效应后的模型为：

1.3 深度生存神经网络Cox模型

DeepSurv是一种深度前馈神经网络［17］，是类似于Faraggi-Simon网络的多层感知器。不同的是加入了多个隐藏层，以及其他新的技术，例如权重衰减正则化、整流线性单位（ReLU）、批处理归一化（Bacth normalization）、dropout、随机梯度下降使用Nesterov动量、梯度修剪和学习率调度等。它通过网络θ的权重参数来预测患者的协变量对其风险率的影响。图1 是DeepSurv 的网络结构，X为输入到网络的患者的基线数据。DeepSurv模型不涉及筛选特征变量，网络的隐藏层使用了一个全连接的节点层（Fully-Connected Layer）和一个dropout 层，交替堆叠。对最后一个dropout 层的输出进行线性组合，最终得到风险率,其估计了Cox 模型中的对数风险函数h(x),通过设置目标函数的平均偏负对数似然来训练网络，其重设计的损失函数如下：

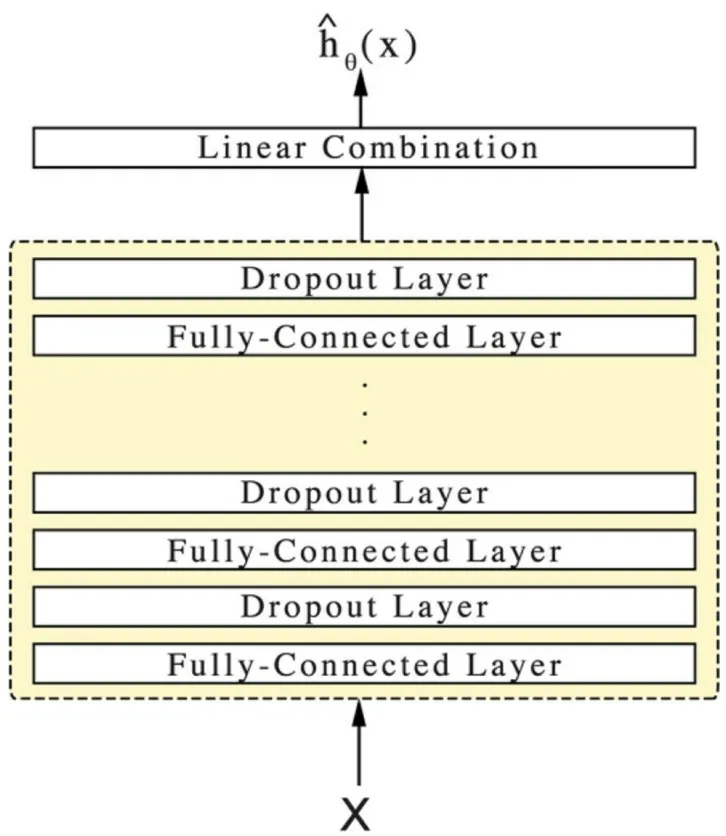
图1 DeepSurv网络结构图Fig.1 Diagram of the structure of DeepSurv.

其中，NE=1是观察到结局的病人例数，E为生存结局，T为生存时间，x为基线特征变量，λ是L2 正则化参数。

在使用深度神经网络时，无论网络有多少层，每一层节点的输入都是上层网络输出的线性组合，需要引入非线性激活函数来拟合非线性关系来提高模型的表达能力，目前为止激活函数种类已超过20种，本文所用的激活函数有Sigmoid、Tanh、ReLU和LeakyReLU，它们的数学形式分别为,本文中a=0.01 。激活函数是向神经网络中引入非线性因素，通过激活函数神经网络就可以拟合各种曲线。激活函数主要分为饱和激活函数（Saturated Neurons）和非饱和函数（Onesided Saturations）。Sigmoid和Tanh是饱和激活函数，而ReLU以及其变种LeakyReLU为非饱和激活函数。非饱和激活函数主要有如下优势：（1）可以解决梯度消失问题；（2）可以加速收敛。Sigmoid极容易导致梯度消失问题。假设神经元输入Sigmoid的值特别大或特别小，对应的梯度约等于0，即使从上一步传导来的梯度较大，该神经元权重(w)和偏置(bias)的梯度也会趋近于0，计算费时并且导致参数无法得到有效更新。ReLU激活函数的提出就是为了解决梯度消失问题；但ReLU会存在神经元“死亡”问题。而LeakyReLU的提出解决了ReLU的神经元“死亡”问题。

2 模拟与实例

2.1 模拟

本研究中的Cox 回归使用R 软件“survival”包实现。限制性立方样条Cox 回归的拟合使用“rms”包完成。随机生存森林（RSF）实现使用“randomForestSRC”包完成。以上均基于R 软件的4.0.3版本。DeepSurv（Cox_DNN）深度神经网络的拟合应用Python 软件3.7.0 版本完成，具体使用的是Pysurvival 库中的NonLinearCoxPHModel 函数。

2.1.1 生存数据模拟设置 在模拟研究中，生成生存时间常使用参数模型，常见的有参数PH模型、AFT模型。参数PH 模型，其参数假定的分布包括指数分布、Weibull分布和Gompertz分布等［18,19］。产生生存数据时，指数分布是最常见的分布假设，但实际数据往往并不满足指数分布，如医药领域常用Gompertz分布来描述数据［20］。因此本研究用Gompertz比例风险模型来产生满足比例风险假设的生存数据。同时本研究也将利用Weibull加速失效时间模型（AFT）产生不满足比例风险假设的生存数据［21,22］。使用Gaussian非线性关联，其公式如下：

其中a表示Gaussian曲线尖峰高度，本文模拟时取值为1；b表示Gaussian曲线中心位置，本文模拟时取值为0；γ表示Gaussian曲线宽度，本文模拟时取值为0.5。

模拟一：

基于Gompertz比例风险模型生成生存时间，假设生存时间与特征变量之间的关系如下：

其中α,λ是分布参数。U为服从[0,1]的均匀分布的随机数。时间T的生存函数可表示为：

本研究使用Gaussian非线性Gompertz比例风险模型来产生满足比例风险假设的生存数据，公式如下：

综上，通过以下过程产生Gaussian 非线性Gompertz PH生存数据：（1）先确定样本量n，并根据生存分布的假设，设定好生存分布参数取值，Gompertz比例风险模型的分布参数α,λ，模拟时分别取0.5，1；（2）通过软件产生服从[0,1]均匀分布的随机数U和服从[-1,1]均匀分布的协变量X；（3）设定好回归系数β的取值，线性变量的系数β取值都为1，非线性变量的系数β#在模拟时分别取值为1，3，6；根据公式5去模拟产生生存时间Ti；（4）根据事先指定的删失时间变量L的分布，以及设置的删失比例F%，本文设置的删失比例分别有10%，20%，40%，60%，80%；通过迭代确定不同删失分布的参数，生成删失时间的n个时间点Li；（5）通过比较Ti、Li的大小，得到每个个体的截尾指示变量δi=Ι[Ti≤Li]，其中Ι[·] 为示性函数。若Ti≤Li，则δi=1，表示终点事件发生，否则δi=0，表示删失。生存时间ti=min(Ti,Li)。最终得到含随机删失的生存数据（ti,δi）。

模拟二：

基于加速失效时间模型(AFT)生成生存时间，假设对数生存时间与特征变量之间的关系如下：

其中σ为尺度参数，εi为随机误差。对于对数线性生存模型来说，时间T的生存函数可表示为εi的生存函数：

若指定随机误差项εi的分布，则称为参数加速失效时间模型。

设置误差项服从极值分布，即f(ε)=exp(ε-exp(ε))，尺度参数σ≠1 时，对应为Weibull回归模型。本研究使用Weibull加速失效模型来产生不满足比例风险的Gaussian非线性生存数据，公式如下：

与前述一样，通过以下过程产生Gaussian非线性Weibull AFT 生存数据：（1）先确定样本量n，以及Weibull AFT模型的分布参数σ，取值为0.1；（2）通过软件产生服从[0,1]均匀分布的随机数ε和服从[-1,1]均匀分布的协变量X；（3）设定好回归系数β的取值，β#在模拟时分别取值为1，3，6，其余β值都为1；根据公式10去模拟产生生存时间Ti；第4和5步与前述Gaussian非线性Gompertz PH生存数据产生步骤一致。

综上，模拟数据主要分为两类，一类是满足PH假定的数据集（模拟一），另一类是不满足PH假定的数据集（模拟二）。模拟总共设置10个变量，其中与生存结局有关的非线性变量1个（x1），线性变量1个（x2），与生存结局无关的线性变量8个，样本量分别设置为200，500，1000。

2.1.2 模型参数设置 模拟时，限制性立方样条节点数统一采用3节点。

对于神经网络参数的设置，由于基线特征变量的数量不多，因此在寻找神经网络最优参数时，各个参数范围分别为隐藏层神经元个数：3、5、7、10、15个；隐藏层层数：1 到5 层；激活函数类型：Sigmoid、Tanh、ReLU 和LeakyReLU；学习率：1e-5,1e-4,1e-3,1e-2,1e-1。使用dropout和正则化技巧避免模型的过拟合，设定dropout比率为0.5，L2 正则化参数为1e-4；默认使用Adaptive Momentum（adam）优化器。

在随机生存森林中，有两个重要的参数，分别是节点预选的变量个数（通常默认最佳的变量个数为全部变量个数的平方根）和随机生存森林中树的数量。通常来说，随机森林中树的数目决定了整个随机生存森林运行效果和时间。在拟合随机生存森林前，必须先确定生存树的个数，本文中当生存树的数量大于500时，错误率已趋于稳定，所以在本文的所有模拟研究中，随机生存森林模型的生存树棵数定为500，节点预选变量数为全部变量的平方根，分裂准则为log-rank。

在预测能力比较的模拟研究中，蒙特卡洛模拟的次数设置为1000次，产生数据总样本量设置为200、500、1000。删失率设置为10%、20%、40%、60%。为了使得四种方法的预测准确度具有可比性并避免过拟合现象，对每次模拟产生的数据集，我们随机选取其中的70%作为训练集拟合模型，剩余的30%作为测试集，得到模型的预测能力评价指标一致性指数（C-index）和积分布莱尔评分（Integrated Brier Score,IBS），最后用所有模拟结果的C-index平均值和IBS平均值分别作为评估指标。

2.1.3 模型评估 在模型预测能力评估中，使用C-index和IBS这两个指标来评价：其中C-index为主要评价指标用于评价模型的预测区分度，IBS为次要评价指标用于评价模型的预测校准度。对于一个疾病预测模型，应先考虑区分度，如果模型区分度较差，不能区分不同风险人群，那么此模型就失去临床应用价值，再继续评价校准度也无意义了。

一致性指数(C-index)最早是由范德堡大学生物统计教授Frank E Harrell Jr 1996年提出，主要用于计算生存分析中的Cox模型预测值与真实之间的区分度，常用在评价患者预后模型的预测精度。C-index的取值范围为[0.5,1]，值越接近于1，表明模型预测准确度越高。Cindex=0.5，表明模型预测为随机预测，预测能力低。可以用以下公式计算［6,23］：

布莱尔评分用于评估在给定时间t的预测生存函数的准确性,它表示观察到的生存状态和预测的生存概率之间的平均平方距离［24］，假设样本量为N，∀i∈[1,N],(xi,ti)分别为第i个个体的预测变量和生存时间，为预测的生存函数，此时布莱尔评分计算公式为：

当存在删失时，需要使用逆概率删失加权法对平方距离进行加权来调整得分，调整后计算公式为：

IBS 提供了在所有可用时间的模型性能的总体计算。

2.2 模拟结果

2.2.1 满足PH假定的情况 图2展示了变量满足比例风险假定时，不同删失率（设置为0.1，0.2，0.4和0.6）和样本量（设置为200，500，1000）情况下4种模型的预测区分度指标C-index和预测校准度指标IBS的变化情况，C-index值越高，模型的预测区分度就越高，模型的预测能力越好。图2的右纵坐标为生存数据产生时非线性变量的系数值（β#）及其余线性变量的系数取值均为1。其中Cox为Cox比例风险回归模型，Cox_DNN为深度生存神经网络Cox模型，Cox_RCS为限制性立方样条Cox模型，RSF为随机生存森林模型。在所有模拟条件下（样本量200-1000，删失率10%～60%），删失率和样本量对Cox_RCS模型预测区分度的稳定性影响不大，此时的Cox_RCS 模型预测区分度始终最好的；Cox_DNN 受删失率的影响较大，当删失率＞40%时，Cox_DNN的预测区分度大幅降低；但当样本量较大（本文≥1000）删失率不高（＜40%）时，Cox_DNN 与Cox_RCS的C-index接近；Cox_DNN在样本量足够大、删失率越低时预测能力会越高。RSF的预测区分度略逊于其他模型。

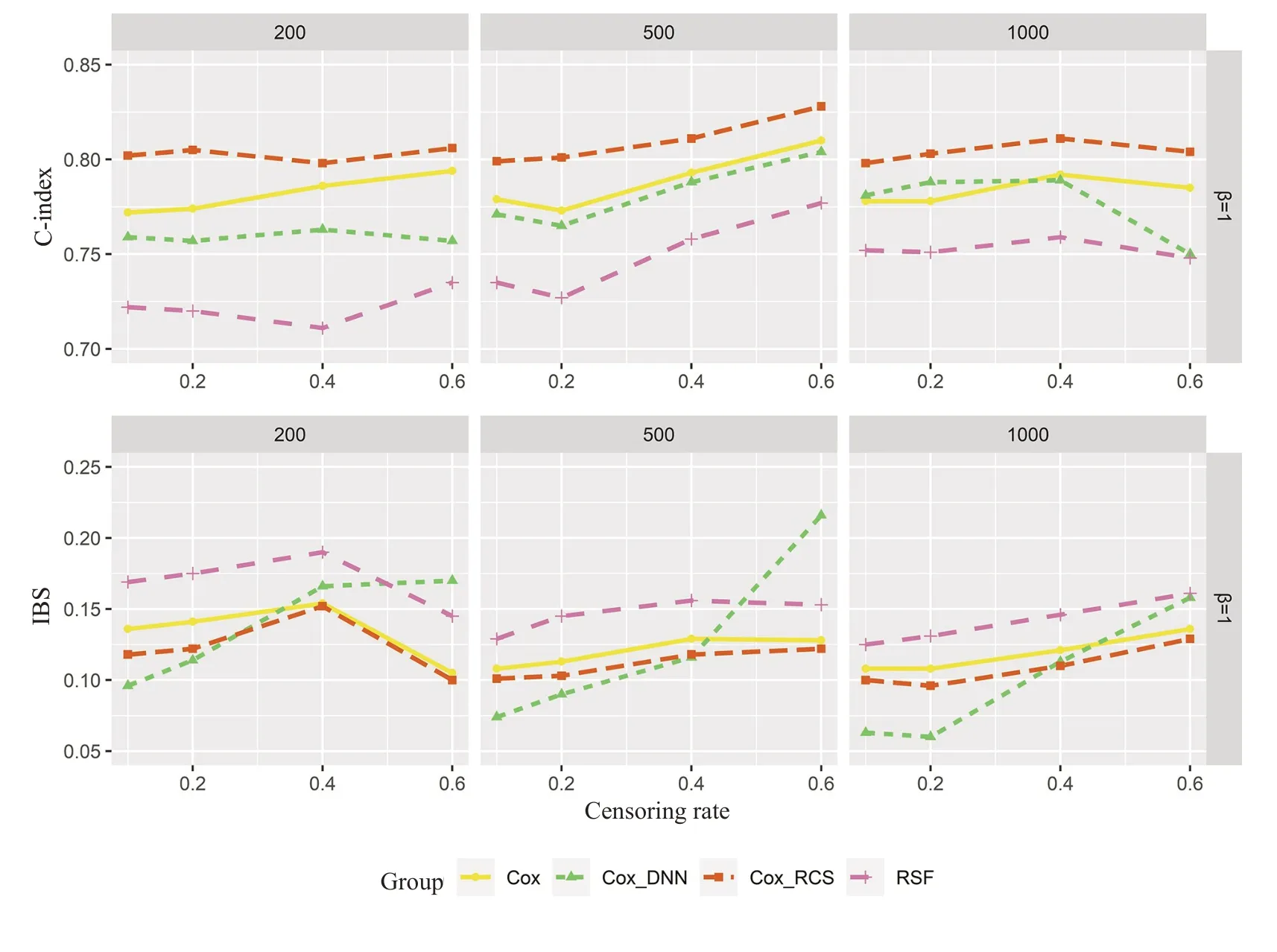
图2 4种方法在非线性变量系数β=1且满足PH模拟数据集中的C-index(上)以及IBS（下）Fig.2 Concordance index (top) and integrated Brier score (bottom) of Cox,Cox_DNN,Cox_RCS and RSF for PH datasets when the nonlinear variable coefficient β=1.

IBS值越低，模型的预测校准度就越好。IBS的结果与C-index一致；删失率和样本量对Cox_RCS模型预测校准度的稳定性影响不大，此时的Cox_RCS模型预测校准度始终是最好的；RSF的预测校准度表现不佳，Cox_DNN 受删失率的影响大，删失率大于40%时Cox_DNN的预测校准度大幅降低。

总之，在满足PH假定的数据中，在预测区分度和测校准度上，Cox_RCS模型预测能力表现最好；在样本量较高（≥1000）、删失率较低（＜40%）时，Cox_DNN模型预测能力与Cox_RCS相当，RSF预测表现不佳。

2.2.2 不满足PH假定的情况 图3展示了变量不满足比例风险假定时，不同删失率（设置为0.1，0.2，0.4 和0.6）和样本量（设置为200，500，1000）情况下4种模型的预测区分度指标C-index和预测校准度指标IBS的变化情况，C-index值越高，IBS值越低，则模型的预测能力就越好。图3的右纵坐标为生存数据产生时非线性变量的系数值（β#）及其余线性变量的系数取值均为1。

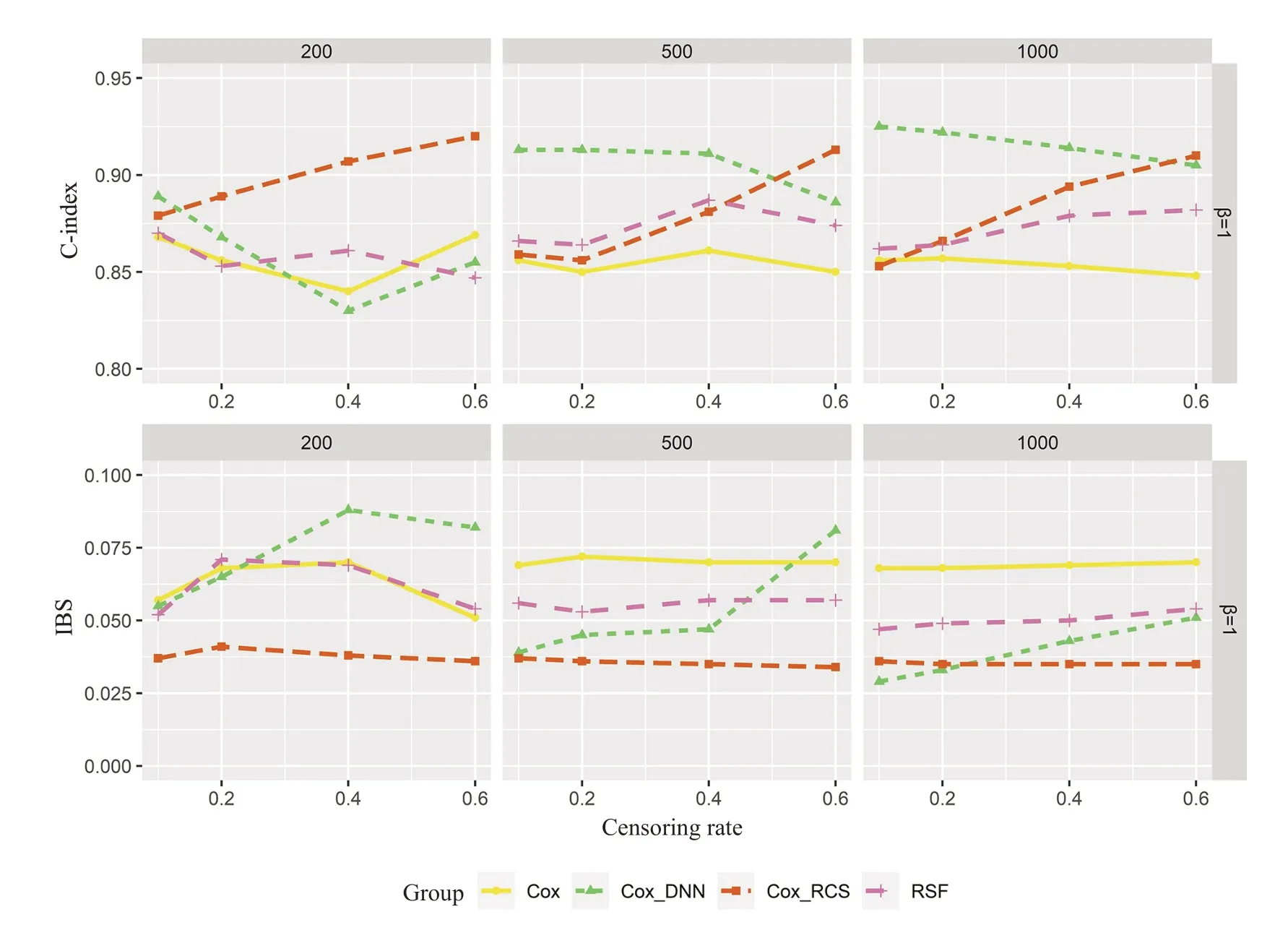
图3 4种方法在非线性变量系数β=1且不满足PH模拟数据集中的C-index（上）和IBS（下）Fig.3 Concordance index(top)and integrated Brier score (bottom) of Cox,Cox_DNN,Cox_RCS and RSF for non-PH datasets when the nonlinear variable coefficient β=1.

在预测区分度上，Cox模型的预测区分度低于其他3种方法，表明Cox模型在不满足比例风险的数据中拟合效果不佳；样本量为200，删失率在0.1～0.6 时，Cox_RCS的C-index值在0.9左右波动，其余3个模型的值都在0.85左右波动，Cox_RCS的预测区分度高于其他3个模型；但是随着样本量增大，Cox_DNN的Cindex 值也在随之增大；当样本量大于等于500 时，Cox_DNN的预测区分度最高；当样本量达到1000时，无论删失率变化如何，Cox_DNN的C-index值能保持在0.9以上；当样本量低于1000时，随着删失率增大，Cox_DNN的C-index值在逐渐降低。这也说明了在不满足比例风险假定的数据集中，模型拟合的不稳定性。

在预测校准度上，Cox_RCS模型的预测校准度高于其他3种方法，Cox模型的预测校准度最低；随着样本量的增加，Cox_DNN的预测校准度也在逐渐升高，删失率的增大会使Cox_DNN的预测校准度降低，但删失率对另外3个模型的预测校准度影响不大；RSF的预测校准度高于Cox模型，低于其他两种模型。

总之，在不满足比例风险的数据中，Cox_RCS在模型预测校准度上占优但在预测区分度上表现不稳定。Cox_DNN的预测校准度受删失率和样本量的影响大；样本量越大（本文中≥500）、删失率越低（本文中＜40%），则Cox_DNN的预测校准度越高。Cox和RSF的预测能力都表现不佳。

2.3 实例

通过实例数据（WHAS500）比较四种方法（Cox,Cox_RCS,Cox_DNN和RSF）的优劣。为防止过拟合现象发生，将随机选取数据集的70%作为训练集训练模型，剩余的30%作为测试集，用C-index和IBS评价模型在测试集中的预测区分度和校准度，对该过程重复1000次，采用箱图展示预测指标C-index和IBS的结果（表1）。

表1 实例数据集中神经网络参数调节范围Tab.1 Adjustment range of neural network parameters in the example dataset

伍斯特心脏病研究数据集（WHAS）包含了500名经历过急性心肌梗死患者，是右删失生存数据［25］，WHAS500 数据集下载网址：https://github.com/rfcooper/whas/blob/master/whas500.csv。500名患者在观察时间内死亡215人，其余患者删失，删失率为57%。生存时间分布如图4所示，中位生存时间为1627 d（生存时间范围：1～2358 d）。表2列出了该数据集生存时间lenfol和删失变量fstat和14个基线变量的基本信息。

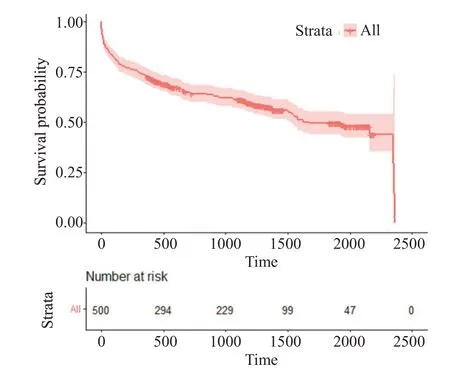
图4 数据WHAS500的生存曲线图Fig.4 Survival curves of WHAS500.

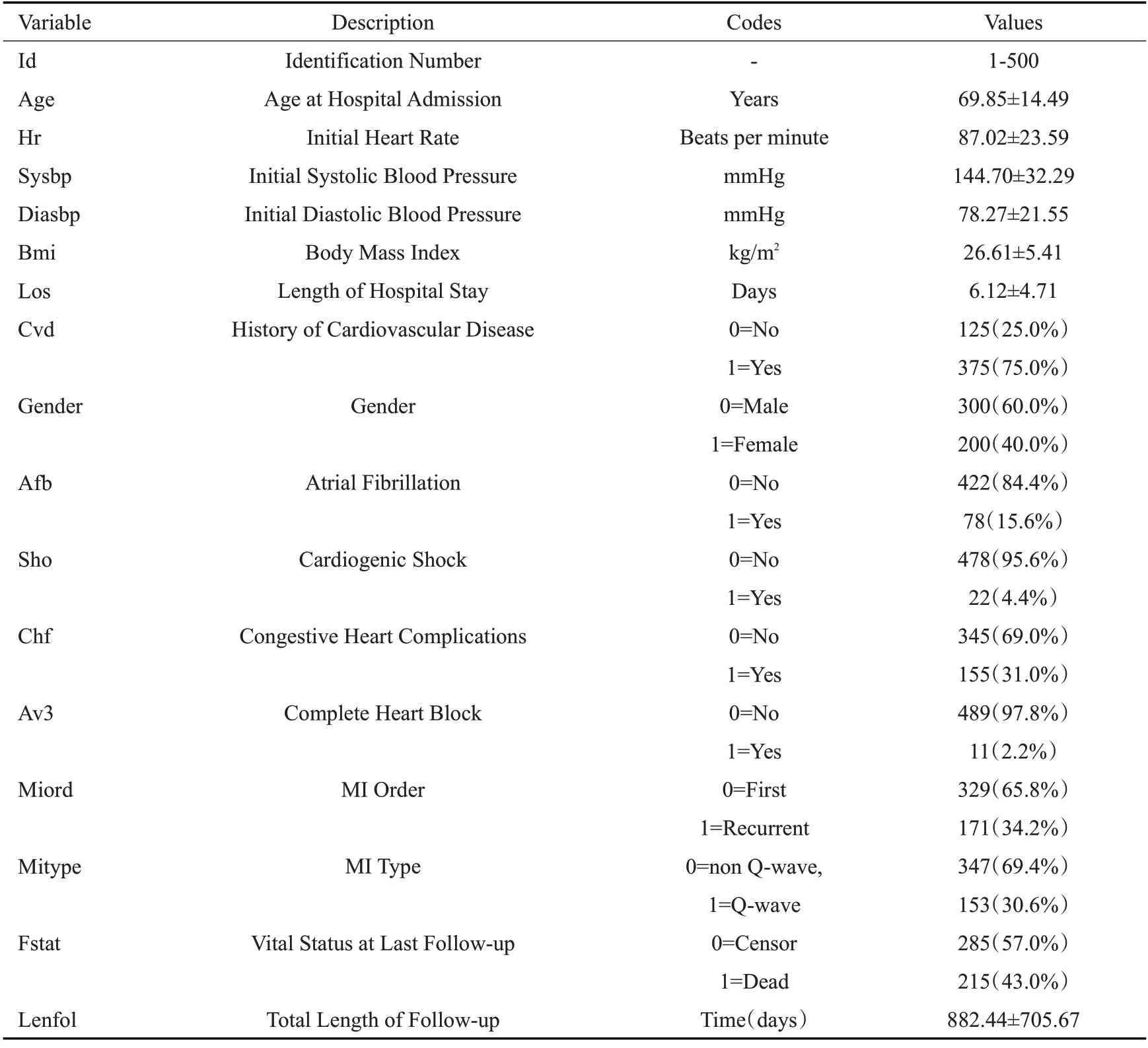
表2 WHAS数据集的基线指标信息分布Tab.2 Characteristics of the covariates in Dataset WHAS[Mean±SD(min～max)or n(%)]

变量选择通过RSF最小深度法变量重要性筛选得出，删除分布严重不均衡的变量sho、av3和重要性排名最末的变量afb和cvd，最终选择纳入模型的变量有10个age,hr,sysbp,diasbp,bmi,los,gender,chf,miord,mitype。用Schoenfeld 残差检查比例风险，结果显示sysbp，mitype这2个变量不满足比例风险假定。

非线性检测显示bmi,los这两个变量为非线性预测变量，经过对比确定bmi的节点个数为3，los的节点个数为4。RSF树的个数在1500之后模型趋于稳定，因此RSF树的个数设为1500，节点为预测变量个数的对数取整数3。表1展示神经网络参数调节范围。通过1000 次对比确定Cox_DNN（DeepSurv）神经网络参数分别设置隐藏层神经元个数为20，隐藏层层数为3，激活函数为tanh，学习率为0.001，其余参数选择默认结果。

从预测区分度上看，C-index值越高模型预测区分度越好，Cox_RCS的预测区分度整体高于其他3个模型，其次是Cox_DNN，但Cox_DNN有较多数值较小的离群值，表现出模型预测的不稳定，由前面模拟可知在删失率较高（＞40%）时，Cox_DNN模型预测效果不佳，而WHAS500的删失率为57%，结果与模拟相符合；Cox和RSF的预测区分度相差不大（图5）。从预测校准度看，IBS 值越低模型预测校准度越好，从图中可看出Cox_RCS 的预测校准度整体高于其他3 个模型，而Cox_DNN的预测校准度最低。综上所述，在含有非线性预测变量的数据中，使用Cox_RCS构建预测模型，其整体的预测准确度都高于其他3类模型。

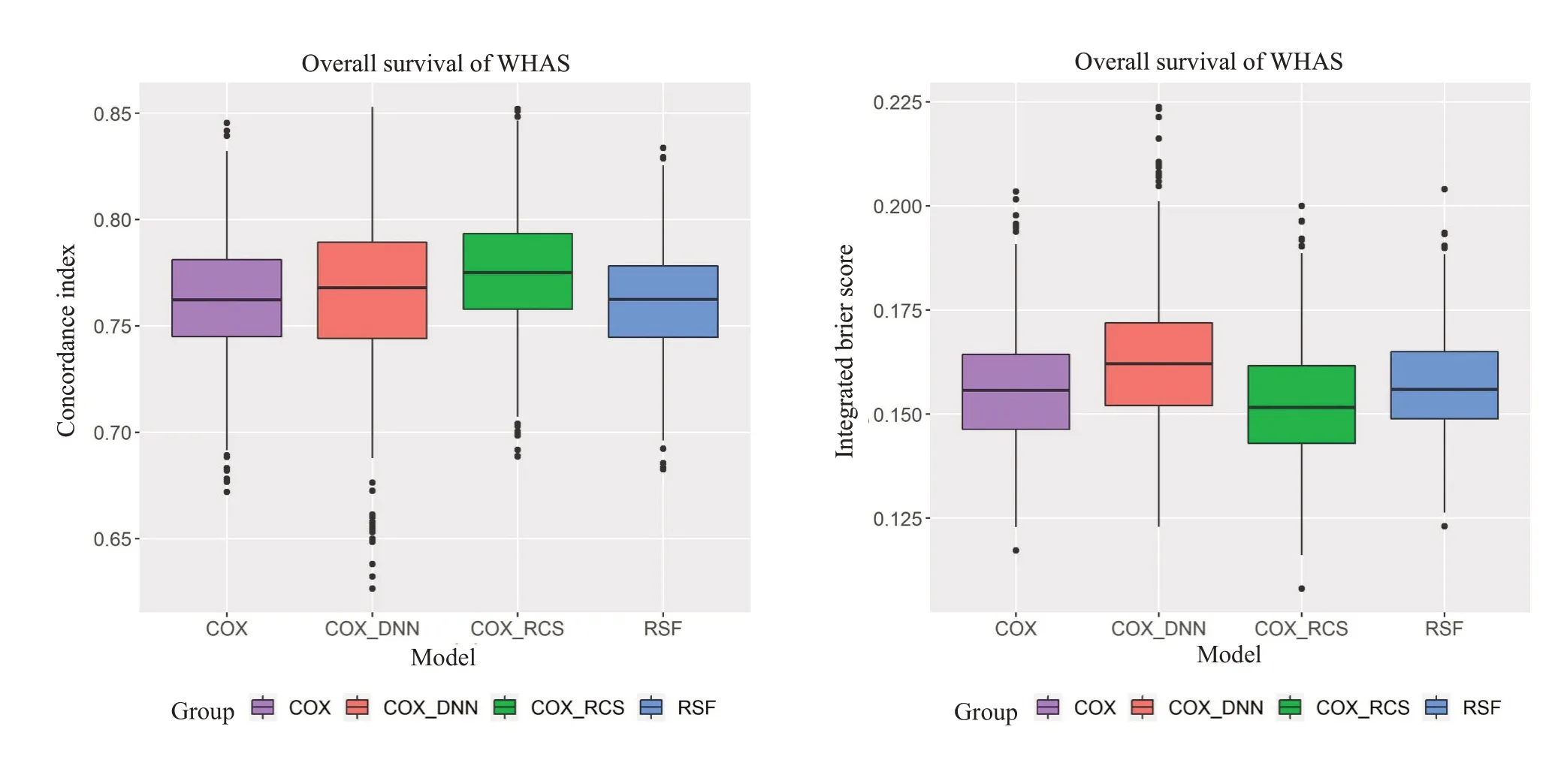
图5 WHAS数据集C-index(左)和IBS(右)的箱图Fig.5 Concordance index(left)and integrated Brier scores(right)of WHAS dataset.

3 讨论

尽管近年来陆续有学者提出深度学习神经网络方法以解决生存分析模型中非线性拟合问题，并且证明了在高维样本数据中深度神经网络方法优于传统的线性Cox回归，但对于扩展的Cox模型如限制性立方样条Cox模型与其他方法之间的比较研究还较少。并且目前还没有研究综合考虑样本量结合删失率时，各方法的优劣情况。

从模拟和实例研究来看，4个模型的预测区分度指标（C-index）和预测校准度指标（IBS），表现最好的是Cox_RCS。综合模拟与实例的结果，Cox_RCS在满足特定条件时的拟合效果优于其它3个模型。因此，对于低维且存在非线性变量的数据，协变量若满足比例风险假定，则推荐使用Cox_RCS。若不满足比例风险假定，高删失率（本文中≥40%）情况下可使用Cox_RCS，若为低删失率（本文中＜40%）且大样本量（本文中≥500），推荐使用Cox_DNN，否则使用Cox_RCS。

当非线性变量存在时，传统的扩展Cox 模型如Cox_RCS便能较好的进行预测，关于各个模型的运行时间和难易程度，Cox_RCS的实现难点是需要筛选出具体的非线性变量，并确认非线性变量是哪几个，而机器学习和神经网络方法都无需识别出具体的非线性变量，而是直接把变量纳入模型进行拟合。Cox_RCS的优点是可以直观了解协变量的表现形式。随机生存森林是机器学习树模型，由树节点不断分裂构成，机器学习方法构建模型前需要调参，如随机生存森林需要确定树分裂的个数以及节点数以达到树模型稳定。深度学习神经网络模型需要对更多的模型参数进行调优，通常可以将调优超参数分为3类：网络参数、优化参数、正则化参数。网络参数包括神经网络的隐藏层层数，每一层的神经元个数，激活函数等；优化参数一般指学习率（learning rate）、批样本数量（batch size）、不同优化器的参数等；正则化参数的设置可以防止模型过拟合，一般包括权重衰减系数，丢弃法比率（dropout）等。因此深度学习神经网络更为复杂，所花费的时间也是最多的。

从结果解释性上看，Cox和Cox_RCS的结果解读起来较为直观易懂，因为其构建的是回归模型，模型拟合的形式较机器学习方法简单，我们能根据每个变量的回归系数直接解释其对生存结局的影响。而Cox_DNN和RSF等机器学习方法使用前需要不断探究最优解的参数，通过建立模型来预测最终结果。但我们无法从机器学习的方法中直接解读每个变量与生存结局的关系，其结果解释性较差。

传统扩展Cox模型的优点是模型较为简单，变量拟合的形式清楚明白，能输出具体每个变量的回归系数，并从中可以得到每个变量对生存时间的影响大小；缺点是无法在高维数据中拟合。随机生存森林的优点是可以高效识别并筛选变量，可以输出变量的重要性排名，适用于高维数据；其缺点是无法直观的得到变量与结局指标的具体表现形式，并且数据的拟合模型在预测上并没有优于其他模型。深度生存神经网络方法优点是可以很好处理大样本数据，并且可以识别图形进行建模；其缺点是数据删失程度对模型影响大，模型较为复杂，并且调参数需要花费大量时间。因此实际应用时需要结合数据，选择适合的方法。