7种单组率的置信区间所需样本量的估计方法比较

于米铼，石晓彤，邹碧清，安胜利

南方医科大学公共卫生学院生物统计学系，广东 广州510515

样本量估计在医学研究中至关重要。其通常有两种估计方法，假设检验法基于显著性检验和检验效能［1,2］计算出所需的样本量。置信区间法关注精确度［3-11］，通过指定置信区间的宽度，计算样本量。在流行病学调查中，研究目的常常是估计某一人群中某特定疾病的患病率［12,13］，流行病学家为了以合理的准确度评估患病率，计算所需的样本量需要用置信区间法。单组率基于置信区间法的样本量估计，在1991年，Lwanga 和Lemeshow给出了基于正态近似的Wald 法样本量计算公式［4］。2008年Machin给出了大样本率下、极端样本率下、有限总体下［14］，基于Wald 法，单组率置信区间法的公式。2013年Vallejo等人给出了基于Wilson Score法置信区间法计算样本量的公式［15］。虽然有众多单组率置信区间的估计方法［16］，现在还没有除了Wald 法和Wilson Score法以外基于置信区间的样本量计算方法。因此，本文拟基于Wald 法、ADD4 法、ADDZ2 法、Wilson Score法、Clopper-Pearson法、Mid-p法和Jeffreys法这7种常见的单组率置信区间估计方法，估算所需样本量并模拟比较，并给出不同情况下的推荐方法，为相关研究提供参考。

1 方法

1.1 单组率的置信区间估计

1.1.1 Wald法（Wald CI）基于正态近似、点估计中心对称理论［17］。如式（1）所示，p表示事件发生率，n表示样本量。

1.1.2 ADDZ2 法（Agresti-Coull add z2CI）Agresti 和Coull提出的ADDZ2法［18,19］，实际是从Wald法入手，将样本成功例数和失败例数都增加。如式（2）所示，其中

1.1.3 ADD4 法（Agresti-Coull add 4 CI）Agresti 和Coull 提出的ADD4 法［18］，在ADDZ2 法中，当α=0.05时，≈4，即将样本成功例数和失败例数都增加2，如式（2）所示，其中x*=x+2，n*=n+4，p*=x*/n*。

1.1.4 Wilson Score法（WS CI）假设事件发生率为π，总体X～B(n,π)，n表示样本量，x表示事件发生数，p=x/n表示事件发生率，如式（3）所示［17］。

可解得π 为

1.1.5 Clopper-Pearson 法（Clopper-Pearson confidence interval）该法可保证置信区间覆盖率在指定概率［20］。区间上限pU和下限pL分别为式（5）的解。

1.1.6 Mid-p 法（Mid-p confidence interval）该 法 是Clopper-Pearson法的矫正，在保证覆盖率的同时可以比Clopper-Pearson法保守性少一点。区间上限pU和下限pL分别为式（6）的解［19,21］。

1.1.7 Jefferys 法（Jefferys confidence interval）假 设X～B(n,p)，p的先验分布为Beta(α1,α2)，那么p的后验分布为Beta(X+α1,n-X+α2)，因此100(1-α)%Bayes 区间为式（7）所示［17］。

1.2 基于置信区间估计的样本量计算方法

本文将采用搜索算法［22,28］对7种置信区间法所需样本量进行估计。

步骤一：给定参数p（预计总体率），ω（置信区间宽度的一半），给n（样本量）一个初始值，假设总体X～B(n,p)，根据7种置信区间估计法，每种方法产生Κ个置信区间。

步骤二：计算出Κ个置信区间宽度平均值2ω*。

步骤三：若2ω*大于（或小于）2ω，则增加（或减少）n的值，重复步骤一和步骤二。

步骤四：重复步骤三直到半区间宽度ω*非常接近给定的ω，即样本量满足n=min{n:|ω*-ω|≤0.001}，得到近似样本量。

步骤五：若达到指定迭代次数，依旧无法达到收敛，则判定样本量估计失败。

2 模拟与实例

2.1 模拟步骤

本研究用R 语言模拟了Wald 法、ADD4 法、ADDZ2法、Wilson Score法、Clopper-Pearson法、Mid-p法和Jeffreys法这7种单组率样本量估计法。模拟步骤如下：（1）固定半置信区间宽度ω，在不同事件发生率p下估计样本量。具体方法见1.2；（2）基于步骤（1）估计的样本量，重复10000次，计算比较各方法的区间覆盖率、置信区间宽度和尾侧不覆盖率比值。考虑事件发生率p在[0,1]范围内基于0.5对称，因此进行参数选择时只考虑[0,0.5]范围内的p。参数设置：ω=0.05、0.1，p=0.01-0.5（间隔0.01），置信水平1-α=0.95。

2.2 评价指标

本研究通过计算在所估计出的样本量下置信区间的区间覆盖率、宽度和尾侧不覆盖率来评估比较各方法。

2.2.1 区间覆盖率（CP）统计上，一个置信区间的覆盖率是它包含感兴趣真值的次数占总次数的比例。区间覆盖率越靠近置信水平越好。I[p∈CI(x;n,α)]为给定X=x，样本量n，检验水准α的条件下，一次模拟研究覆盖情况的示性函数，置信区间包含事件发生率时，即p∈CI(x;n,α)，I[p∈CI(x;n,α)]取值为1，否则为0，如式（9）所示。

若给定的置信水平为95%，则覆盖率越接近95%，置信区间估计越好。当覆盖率小于94%时，认为覆盖率较差。当覆盖率大于96%时，认为区间估计较保守。本研究中，以覆盖率在[0.94,0.96]定义为较好。

2.2.2 置信区间宽度（CW）如式（10）所示，其中U(x)和L(x)分别表示置信区间的上限和下限。

本研究中，在保证区间覆盖率的前提下，由于事先指定了半置信区间宽度（ω=0.05,0.1），模拟过程中若半区间宽度估计误差值在0.001 之内，则所估计的样本量将被接受。因此主要考察估计出的样本量计算的置信区间宽度是否在指定范围[0.098,0.102]，[0.198,0.202]之内，若在指定宽度范围之内，则认为样本量估计精确。

2.2.3 左右尾侧不覆盖率（MNCP，DNCP）置信区间下限大于真值的概率称为MNCP，置信区间上限小于真值的概率称为DNCP，见式（11）。左右尾侧不覆盖率应尽可能接近，越接近说明置信区间对称性越好。

2.2.4 尾侧不覆盖率比值：MNCP/（MNCP+DNCP）越接近0.5说明置信区间的对称性越好。在本研究中，当尾侧不覆盖率比值在0.4～0.6间，认为该方法的对称性较好。

2.3 模拟结果

2.3.1 样本量估计失败情况 如表1 所示的半置信区间宽度和事件发生率的情况下，估计样本量失败，因而均不计算置信区间宽度，覆盖率，尾侧不覆盖率比值。

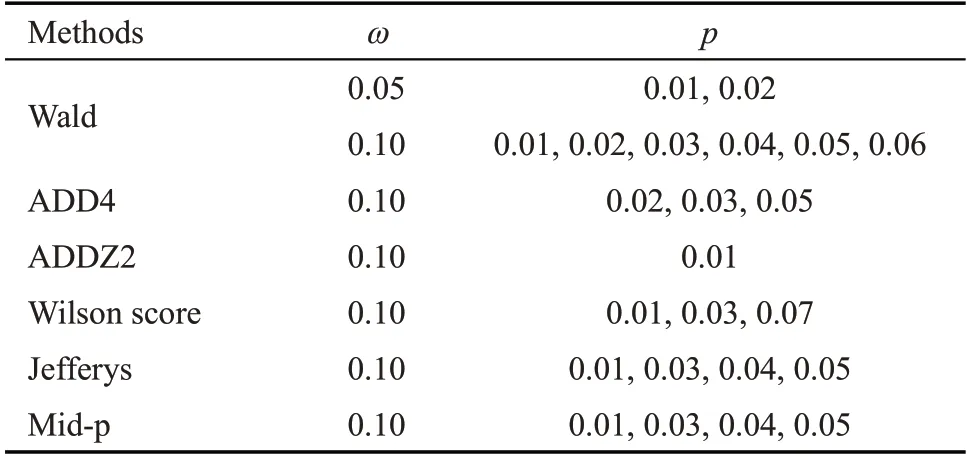
表1 样本量估计失败情况汇总Tab.1 Summary of failure of sample size estimation

2.3.2 样本量比较 随着事件发生率的增加，样本量逐渐增加（图1）。Clopper-Pearson法所估的样本量明显大于其他方法，其他方法计算结果相近。

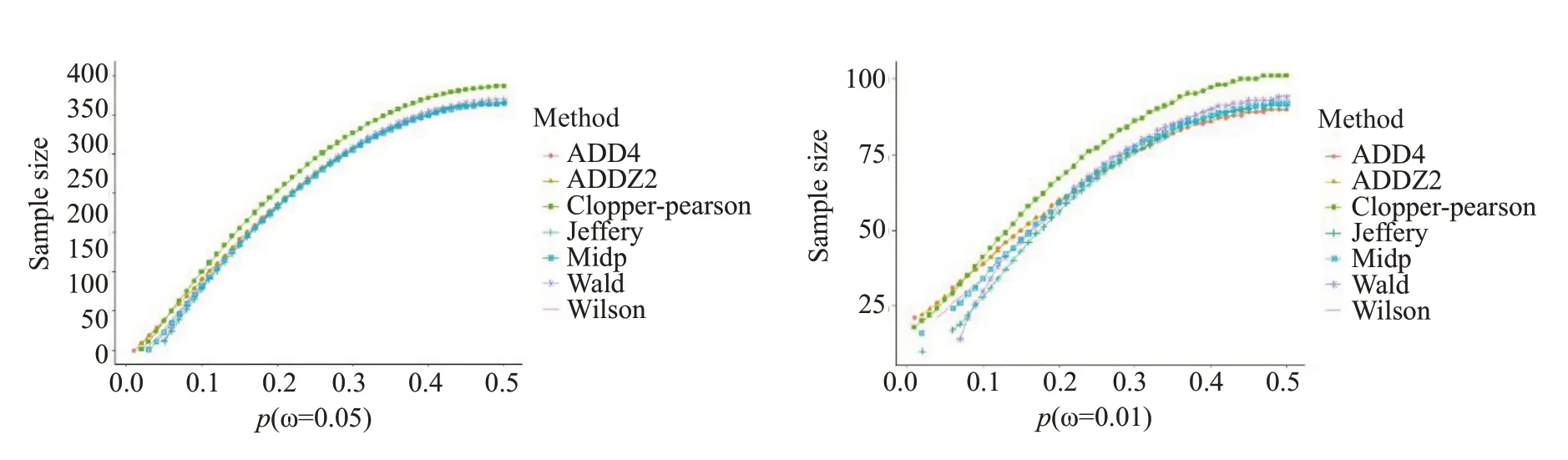
图1 样本量随事件发生率p的变化情况Fig.1 Influence of p on sample size estimation(ω=0.05,0.1).

2.3.3 区间覆盖率（CP）比较 在ω=0.05时，在低事件发生率p=（0.01-0.1）时，建议选择覆盖率较保守的ADD4法、ADDZ2法和Clopper-Pearson法。而Mid-p法偶尔发生覆盖率低于0.94，也可参考选择。在其余情况下，除了Clopper-Pearson法较保守，其他方法的覆盖率都相对稳定，Mid-p法和Jefferys法偶尔发生覆盖率低于0.94的情况（图2）。

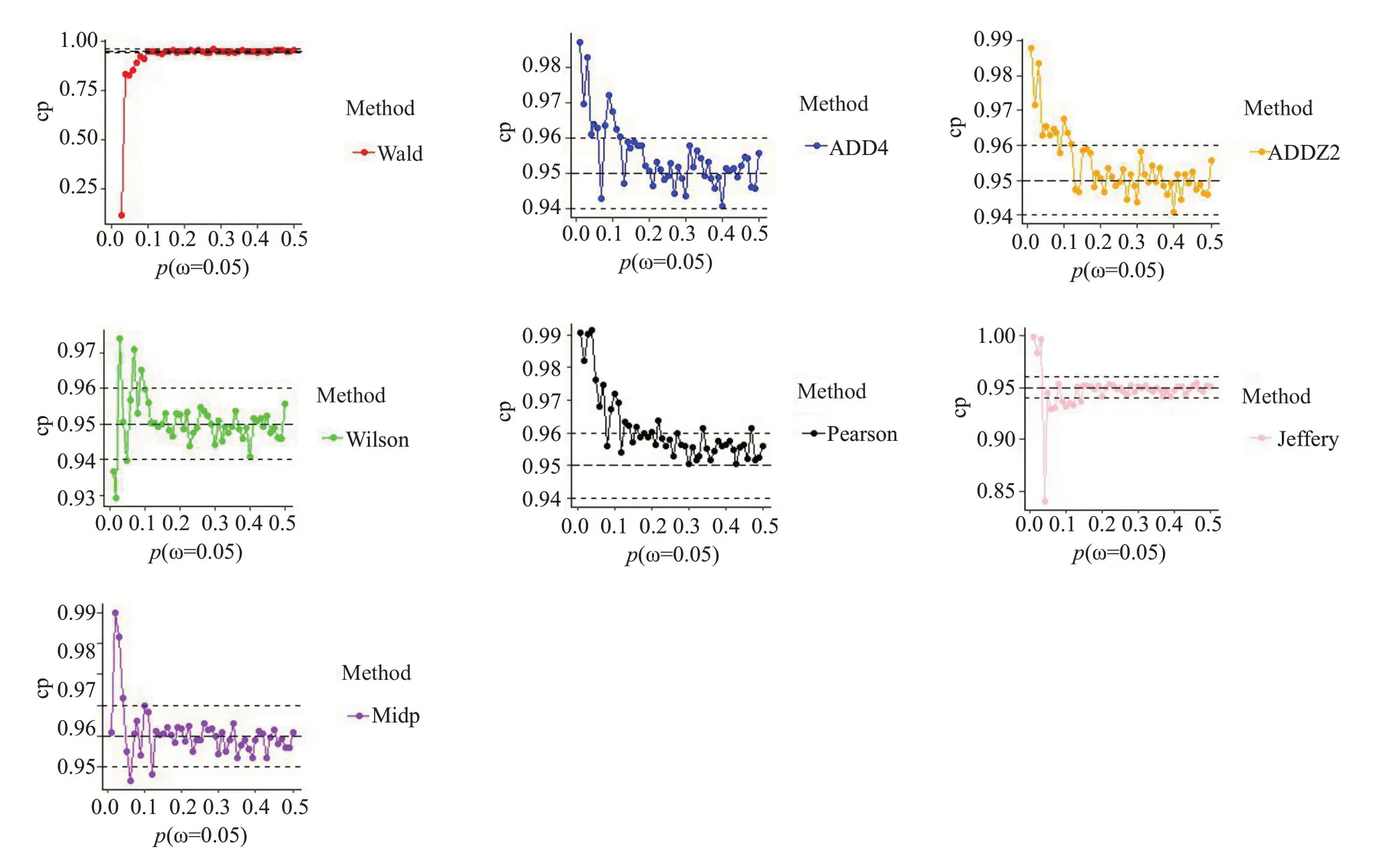
图2 区间覆盖率(CP)随事件发生率p的变化情况Fig.2 Influence of event probability(p)on coverage probability(ω=0.05).

在ω=0.1时，在事件发生率极低p=（0.01-0.05）时，除Clopper-Pearson法外，其余方法都存在无法迭代的情况，建议选择Clopper-Pearson 法。其他情况与ω=0.05的情况类似，不多赘述。

2.3.4 尾侧不覆盖率比值(MNCP/(MNCP+DNCP))的比较 在ω=0.05时，当事件发生率极低时p=（0.01-0.05），所有方法的对称性表现都不好。在p=（0.05-0.15）时，Mid-p 法和Clopper-Pearson 法的对称性较好。在p=（0.15-0.3）时，除了Wald 法，其余方法都可以选择。Wilson Score法、Jefferys法偶尔存在尾侧不覆盖率比值不在指定范围的情况。在p=（0.3-0.5）时，所有方法对称性都在指定范围，都可选择（图3）。

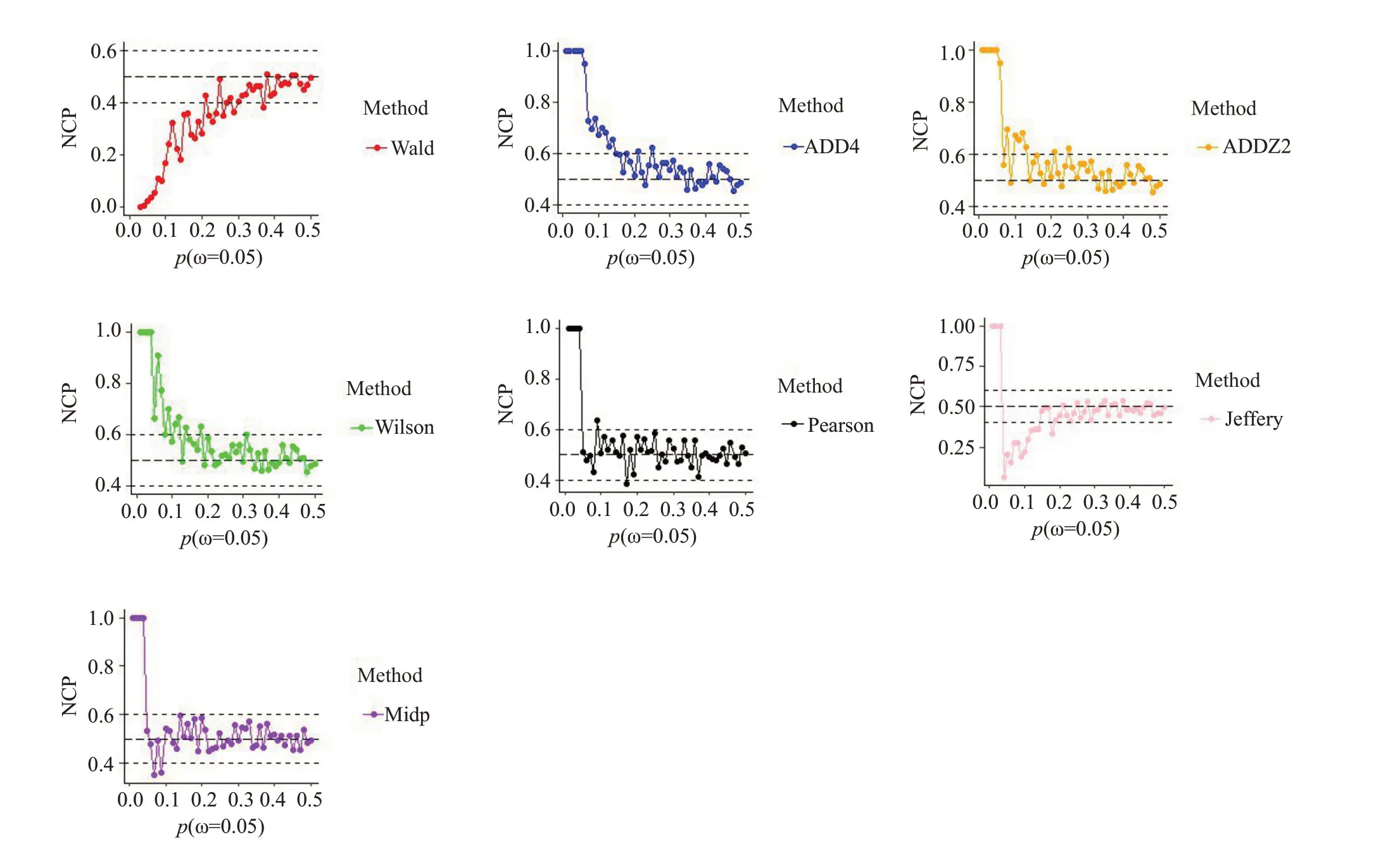
图3 尾侧不覆盖率比值(NCP)随事件发生率p的变化情况Fig.3 Influence of p on noncoverage probability (ω=0.05;NCP=MNCP/(MNCP+DNCP)).

2.3.5 置信区间宽度（CW）的比较 随着事件发生率的增加，各方法的置信区间宽度逐渐趋于指定宽度，有些方法会在事件发生率p较低时，宽度大于指定范围，但误差尚在0.001内，故基本认为各方法无明显差异（图4）。

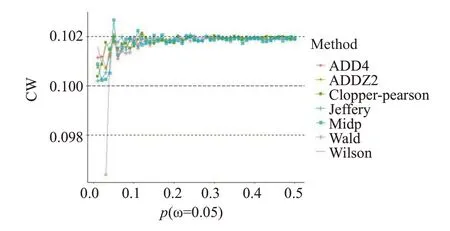
图4 置信区间宽度(CW)随事件发生率p的变化情况Fig.4 Influence of p on confidence interval width(ω=0.05).

2.4 实例分析

本文采用Lwanga在样本量计算指南中的例子［4］。

卫生部门希望估计当地五岁以下儿童的结核病患病率。如果已知真实率不太可能超过20%，那么应调查多少儿童，以便在95%的置信度下，将患病率估计误差控制在真实值的5%以内。即事件发生率p=0.2，ω=0.05（表2）。

表2 不同方法所估计出的样本量及有关指标Tab.2 Sample size and relative indexes estimated by different methods

可见，Clopper-Pearson法计算的样本量明显大于其他方法。所有方法的置信区间宽度都在指定范围内。综合考虑区间覆盖率和尾侧不覆盖率比值，建议选择ADDZ2法，它的区间覆盖率接近0.95，尾侧不覆盖率比值最接近0.5。ADD4 法和Mid-p法表现也相对较好。与模拟结论一致。

3 讨论

本文从常用的7种单组率置信区间估计法入手，通过迭代计算，得到了基于置信区间估计的样本量计算方法，并模拟比较了在不同精度（ω=0.05，0.1）、不同事件发生率下各种方法计算得出的样本量。

在推荐方法的选择时，由于各方法区间宽度无明显差别，因此建议先考虑区间覆盖率，再考虑对称性，最后考虑置信区间宽度。若有多个方法入选，用户可以自行选择。

当精度要求较高时（ω=0.05），若事件发生率在p=（0.01-0.05）时，所有方法对称性都较差，Mid-p法、Clopper-Pearson法、ADD4法、ADDZ2虽然覆盖率较高（保守），但是综合表现最优，建议选择。在p=（0.05-0.15）时，Mid-p法表现最优。在p=（0.15-0.3）时，除了Wald 法，其余方法表现差异不大，Wilson Score 法和Jefferys法偶尔存在尾侧不覆盖率不在指定范围情况，也可以参考选择。在p=（0.3-0.5）时，所有方法表现差异不大，都可以选择。

当精度要求适中时（ω=0.1），在事件发生率极低p=（0.01-0.05）时，除Clopper-Pearson法，其余方法都存在无法迭代的情况，建议选择Clopper-Pearson法。其余情况与ω=0.05类似。

由于Clopper-Pearson法覆盖率有时过高，导致估计结果过于保守，使计算出的样本量大于其他方法，考虑其成本效益，在有别的方法选择时，建议选择其他方法。Mid-p法的计算方法运算比较缓慢，在实际应用中也应考虑这一点。

当ω=0.1且事件发生率较低（小于0.1）时，有较多方法估计样本量失败，可能的原因是置信区间法首选需固定置信区间宽度，而方法本身可能无法产生满足该区间宽度的样本量估计结果。同时，为了满足指定的区间宽度，可能会导致区间对称性较差。因此在此条件下，不推荐本研究中涉及的置信区间法进行样本量估计。

本文仍有值得继续探索的地方。

（1）单组率的置信区间估计方法众多［16］，本文只是挑选了其中代表性的方法，仍有其他方法估计样本量值得探寻；（2）本文样本量估计是基于搜索迭代法，部分方法在运算时存在运算缓慢的情况，有的置信区间估计法甚至会无法得出结果。有的学者是从置信区间估计公式本身出发［3,4,13,29］，通过列等式换算，给出样本量的计算公式，在此基础上做出矫正，但该方法不适用于置信区间估计方法较复杂、无法直接样本量计算公式的情况，需要进一步探索如何基于置信区间估计计算样本量的其他方法［30］，如鞍点逼近法等等；（3）基于置信区间宽度（精度）的设置，本文只设置了2 种情况，即ω=0.05 或0.1。还可设置更多情况，以探索不同精度下的各方法的优劣。