基于检测支柱偏移的球罐屈曲分析
2023-02-27易天坤欧晨希林冠堂
黄 思,易天坤,欧晨希,林冠堂
(1.华南理工大学 机械与汽车工程学院, 广州 510641; 2.广东省特种设备检测研究院珠海检测院, 广东 珠海 519002)
0 引言
球罐被广泛应用于石化行业,主要用于储存液化石油气[1]。当施加到结构上的载荷达到某一值时,若继续增加微小的载荷,结构的位移会发生很大的改变,称结构发生了屈曲或者失稳。由于受到安装施工和土壤等环境的影响[2],球罐支柱将产生沉降和偏移。球罐支柱的沉降和偏移一旦达到一定程度时,球罐可能因局部受力不均而发生屈曲变形和破坏。
国内外学者相继开展了圆柱罐和球罐在沉降下的静力学和屈曲研究。静力学研究方面,周蓓蓓等[3]采用有限元法研究了支柱沉降形式对球罐总体应力分布的影响;Yang等[4]采用有限元法计算了支柱不均匀沉降下的球罐应力和支柱位移;Gao等[5-6]研究了球罐支柱沉降对球壳和支柱应力的影响;房江祥[7]运用ABAQUS软件模拟了1.5 m3球罐的支柱沉降对其拉杆应力和极限载荷的影响;Chen等[8]通过ANSYS软件建立了圆柱罐的有限元模型,研究了圆柱罐在不均匀沉降下的变形行为。屈曲研究方面,Jonaidi等[9-10]采用有限元与实验验证相结合的方法,研究了圆柱罐在谐波沉降下的屈曲响应;Godoy等[11-12]通过实验方法研究了局部沉降下圆柱罐的屈曲响应;范海贵[13]采用现场实测、理论推导和有限元数值模拟相结合的方法,研究了圆柱罐在沉降和轴向载荷联合作用下的屈曲行为;赵阳等[14]分别研究了整体沉降和局部沉降下圆柱罐的屈曲变形行为。
综上所述,现有研究主要是针对圆柱罐和球罐在沉降下的静力学和屈曲研究,还未对球罐支柱在偏移下的静力学和屈曲进行过研究。因此,根据现场检测的球罐支柱偏移数据,开展球罐在支柱偏移下的屈曲研究,求解计算球罐支柱偏移的极限值。该极限值可为现场监测数据提供理论参考和作为实时监测的警戒值,为预防球罐在支柱偏移下发生屈曲失效而引发重大安全事故具有重要意义。
1 计算模型
图1是根据表1[15]球罐的设计参数所建立的球罐三维模型,其材料特性参数见表2。

表1 丙烷球罐设计参数

图1 球罐三维模型示意图
表2 球罐主要结构的材料特性参数
2 屈曲响应分析
2.1 网格划分
运用Workbench平台中Mesh对图1的计算模型进行网格划分,为避免网格数对计算结果的影响,需考察计算域在不同网格数下的计算结果。考虑到本文仅对球罐进行屈曲变形的研究,图2给出了通过Workbench平台计算得到的球罐的最大总位移xmax随网格数的变化规律。
从图2可知,当球罐的网格数达到85万之后,球罐最大总位移xmax值基本稳定。考虑到计算精度和成本,选用988 554为球罐计算域的网格数,模型网格划分结果见图3。

图2 网格无关性检验曲线

图3 球罐网格划分结果示意图
2.2 载荷与约束条件
考虑球罐充装率φ为90%的工况,球罐的载荷有重力G、内壁压力p。其中压力p随液下深度h的变化规律为:

(1)
式中:po为球罐的工作压力,为1.42 MPa;ρl为液态丙烷的密度,为474.04 kg/m3;g为重力加速度,取9.81 m/s2;H为充液高度,其中H与φ有如下关系[16]:
(2)
式中:R为球罐的内半径。
图4给出了12根支柱编号的示意图。分别单独研究单根支柱沿着周向偏移和径向偏移情况。周向偏移是指支柱底部沿着图4以O为圆心的大圆圆周方向的偏移,定义顺时针方向为正,逆时针方向为负。径向偏移是指支柱底部沿着以O为圆心的大圆半径方向的偏移,定义向内偏移为正,向外偏移为负。根据现场检测的支柱偏移数据,支柱的偏移量一般在30 mm以内。根据周向偏移的对称性,对于周向偏移仅考虑正偏移的情况。因此,设置的单根支柱的周向偏移量Wt和径向偏移量Wr见表3、4。

图4 支柱编号示意图

表3 单根支柱周向偏移量
2.3 屈曲分析原理
按照临界状态的特性,屈曲可分为跳跃屈曲、极值屈曲和分支屈曲,分别对应图5中的(a)、(b)和(c)所示的载荷P—位移x曲线[17]。图5中的载荷P为广义载荷,可以是力载荷或是位移载荷等,本文研究的载荷为球罐支柱偏移的位移载荷。

图5 不同屈曲特性的载荷P-位移x曲线
当球罐支柱的偏移达到一定水平时,球罐在自重G、内壁压力p和支柱偏移Wr和Wt等作用下将发生整体或局部弯曲大变形。因此,需对球罐开展屈曲分析,确定其支柱偏移的极限值。针对球罐的屈曲分析可采用“弧长法”。“弧长法”最初是由Risks等提出[18],后经Roma等[19]逐步改进而完善。弧长法是目前结构屈曲分析中效率较高的一种方法。
弧长法中非线性平衡方程组一般可以表示为:
K·x=F
(3)
式中:矩阵K为切向刚度矩阵,向量x为节点位移,向量F为外载荷。现将方程写成增量形式,并引入载荷因子λ,则平衡方程:
K·Δx=ΔλF
(4)
此时平衡方程共有n+1个未知量:Δx1,Δx2,…,Δxn,λ,而方程数只有n个,因此需再补充一约束条件:
Δλ2FTF+ΔxTΔx=Δl2
(5)
弧长法的求解流程如图6(a)所示,通过该流程的求解得到完整的λ-xmax曲线。如图6(b)所示,弧长法是利用平衡方程和弧长约束条件寻找平衡点的过程。由图6(b)、表3和表4中的球罐支柱的偏移是逐步加载的。当支柱加载的偏移量超过C点所对应的极限值时,球罐某些部位将会突然丧失原有的几何形状,发生大幅的屈曲变形,即C点后球罐发生了屈曲。基于弧长法的数值模拟方法,首先分别单独研究球罐在单根支柱底部周向偏移和径向偏移下的屈曲响应过程,然后根据现场检测的支柱偏移数据,开展球罐在支柱偏移下的屈曲研究。

表4 单根支柱径向偏移量

图6 弧长法迭代求解过程
3 支柱偏移的屈曲分析
在应用Workbench平台对球罐进行屈曲响应分析时,分别单独将表3和表4中球罐支柱的偏移逐步加载。载荷因子λ表示球罐屈曲响应过程中支柱偏移的加载比例,例如λ=0.5时,球罐支柱加载的偏移分别为0.5Wr和0.5Wt。当λ从0增大到1时,意味着球罐支柱的偏移全部加载完成。
图7是将表3中的数据逐步加载并求解得到的单根支柱底部周向偏移的λ-xmax曲线,其中xmax为最大总位移,λ为载荷因子。图8为该状态下的曲线中A、B、C和D四点处的变形云图,其中A、B、C和D四点对应的λ值分别为0.05、0.15、0.25和0.55。

图7 单根支柱底部周向偏移下的λ-xmax曲线

图8 单根支柱底部周向偏移下球罐屈曲响应的变形云图(变形缩放系数=20)
对照图7与图5可知,该球罐在支柱底部周向偏移下的屈曲响应符合分支屈曲的特点,在C点前球罐的变形随支柱底部周向偏移的增大呈线性变化,说明球罐处于平衡状态,还未发生屈曲。C点时球罐的变形云图如图8(c)所示,对应的最大总位移为7.5 mm(在支柱1的底部)。当支柱底部周向偏移超过C点对应的极限值(λ>0.25,即Wt>7.5 mm),球罐局部位移突变发生了屈曲,如图8(d)所示,此时最大总位移为102.8 mm,屈曲的位置在支柱1与支柱2之间的拉杆处。
图9是将表4中的数据逐步加载并求解得到的在单根支柱底部径向偏移下的λ-xmax曲线。图10为单根支柱底部径向内偏移的曲线中A、B、C和D四点处的变形云图,其中A、B、C和D四点对应的λ值分别为0.25、0.5、0.75和0.9。

图9 单根支柱底部径向偏移下的λ-xmax曲线
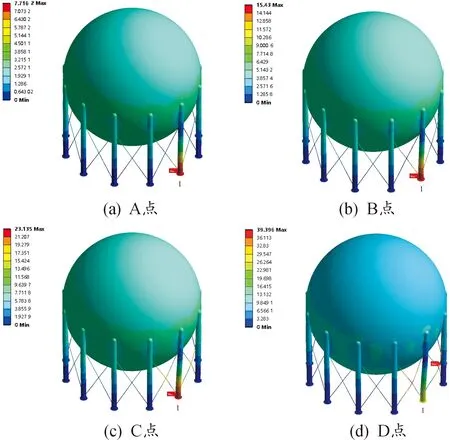
图10 单根支柱底部径向内偏移下球罐屈曲响应的变形云图(变形缩放系数=20)
从图9可知,支柱底部径向外偏移时未出现位移突变,表明支柱底部径向外偏移在现有数据范围内还未使球罐发生屈曲。将图9与图5进行对照可知,该球罐在支柱底部径向内偏移下的屈曲响应符合分支屈曲的特点。在C点前球罐的变形随支柱径向偏移的增大呈线性变化,这时球罐处于平衡状态未发生屈曲。C点时球罐的变形云图如图10(c)所示,对应的最大总位移为23.1 mm。当支柱径向内偏移超过C点时对应的极限值(λ>0.75,即Wr>22.5 mm),球罐局部发生了屈曲,如图10(d)所示,此时最大总位移为39.4 mm,屈曲的位置在支柱1与支柱12之间的拉杆处。
4 检测支柱偏移的屈曲分析
全站仪具有高精度、高稳定性和高可靠性技术等优点,极其适合用于球罐支柱偏移位移的测量。对现场球罐支柱的偏移数据的测量工作采用徕卡TCR1202+R1000电子全站仪,其测量的精度为1 mm。表5是用该仪器在现场测量的支柱偏移数据。

表5 现场检测的球罐支柱偏移值 mm
为了模拟球罐在检测支柱偏移下的屈曲响应过程,将表5中的球罐支柱的偏移逐步加载,在Workbench平台运用弧长法进行求解计算。图11是通过求解得到的球罐在检测支柱偏移下的λ-xmax曲线。图12为该情形下的曲线中A、B、C和D四点处的变形云图,其中A、B、C和D四点对应的λ值分别为0.1、0.3、0.5和0.7。

图11 检测支柱偏移下的λ-xmax曲线
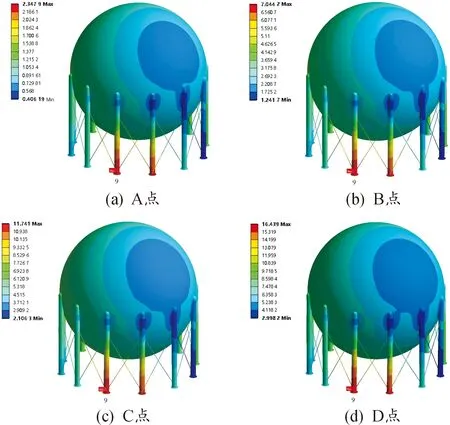
图12 检测支柱偏移下球罐屈曲响应的变形云图(变形缩放系数=20)
由图11可知,球罐的变形随支柱偏移的增大呈线性变化,直到支柱的偏移加载完成都未出现明显的位移突变,说明球罐在该情形下并未发生屈曲。分析其原因,发现所测球罐支柱底部的径向偏移数据均是30 mm以内的外偏移,由数值求解结果可知球罐在30 mm内的径向外偏移不发生屈曲。同时球罐支柱底部的周向偏移仅有支柱4、7和8超过了数值计算结果的极限值7.5 mm,加之支柱的相互约束使支柱之间的周向偏移实际未超过极限值。
5 结论
1) 在所研究的偏移量范围内支柱底部径向外偏移未出现屈曲。支柱底部径向内偏移的极限值比底部周向偏移的极限值大,支柱底部径向内偏移的屈曲变形量比底部周向偏移的变形量小,说明球罐支柱底部在周向偏移时更容易屈曲,在支柱底部径向外偏移最不易屈曲。
2) 球罐的屈曲变形最大的位置位于拉杆处,屈曲变形较大的位置是偏移的支柱与球壳的连接处。该球罐在支柱底部径向内偏移和周向偏移下的屈曲响应均符合分支屈曲特点。
3) 根据现场检测的球罐支柱的偏移数据,求解发现该球罐未发生屈曲变形,仍属于小幅弹性变形。
