Paden-Kahan第二子问题扩展问题求机械臂逆运动学研究
2023-02-27张树刚吕北轩隋丽君
张树刚,吕北轩,李 勇,隋丽君
(呼伦贝尔职业技术学院机电工程系,内蒙古 呼伦贝尔 021000)
1 国内外相关研究概述
自2020年初新型冠状病毒肺炎疫情爆发以来,在疫情的冲击下,制造业企业的发展面临着具备一定操作技能的操作者短缺的“用工荒”及在岗员工感染新冠病毒的双重风险的掣肘。当前,中国所取得的抗疫阶段性胜利的经验表明了,最有效地控制疫情的方法就是隔离以及保持社交距离。现如今疫情等客观条件势必将倒逼制造业企业向数字化、智能化生产的转型,推进少人化生产和柔性制造,即使企业提升自身抗风险能力的同时,也有利于提高生产效率。在抗疫常态化、制造业少人化的背景下[1-2],由一些系列关节串接而成的多关节工业机械臂,作为智能化生产的数字化车间设备拓扑层上的关键物理组元[3-4],显然已经成为了这场“减人不减效”的抗疫战争中的关键设备。运动学逆解是机械臂进行工作轨迹规划及优化工作效率的理论前提[5],高效率求运动学逆解的方法将显著提高机械臂的工作效率,进而有利于提升制造业企业复工复产的进度。当前学界业内的相关研究主要集中在对机械臂逆解的具体的算法与存在性上。对于逆解的具体的运算上,当前主要采用两种方法构建机械臂运动学模型,即Denavit-Hartenberg 法与旋量理论法,并且大量的学者已进行了相关的研究,并已做出大量的应用。这里根据文献[5-7],总结出Denavit-Hartenberg法与螺旋理论的特性,具体如表1所示。

表1 Denavit-Hartenberg法与螺旋理论的特性Tab.1 Characteristics of Denavit-Hartenberg Methods and Screw Theory
由上表可知螺旋理论相比Denavit-Hartenberg法而言,其具备着较为明确的几何意义与直观性,并减少了繁琐的坐标系构建与关节坐标变换过程,求解的运算效率较高。当前,国内外诸多学者已采用了旋量指数积(POE,Product of Exponentials)对串联机构的运动学进行了大量的分析与研究。文献[8]运用旋量指数积,对数字化脑立体定向仪,这一串联结构构建了运动学方程,并避免了各个构建繁琐的坐标系构建与坐标变换。文献[9]成功地运用螺旋理论对安川MH6 型机械臂构建了运动学模型,并用八组逆解验证了旋量理论逆运动学求解的有效性。文献[10]针对后三关节轴线交于一点的6R串联机械臂,将Paden-Kahan子问题结合消元法,提出了一种逆解算法,并通过实例得到了验证。文献[11]在旋量理论的基础上结合数学吴方法对机器人逆解问题进行了改进,实际表明该方法具备较强的准确性与效率。可见,旋量理论已在学界业内得到了广泛的应用。但旋量理论的逆解亦具备一定局限性,如在文献[12]中,指出该团队所研制的一种具备多轴线平行的新型机械臂难以运用经典的Paden-Kahan 子问题直接进行解决。简而言之,旋量理论机械臂逆解的基础Paden-Kahan 子问题,只能解决特定的自由度较低串联机构的逆解问题[10]。
这里运用旋量运动理论,将串联机械臂各个运动副与连杆的运动,转换为旋量指数积构建出了串联机械臂的正逆运动学。并在Paden-Kahan第二子问题的基础上,提出了其第二子问题的一种新的扩展问题,实现了对其经典问题进行补充。最后以ABB IRB2600型机器臂作为验证对象,通过第二子问题的一种新的扩展问题对其进行求逆运算,在经过对6组解验证后,验证了这里提出的Paden-Kahan第二子问题的扩展问题在串联机械臂逆运动学求解方面应用的有效性。
2 机械臂旋量系坐标建立及其运动学构建
设空间中的一物体发生旋转后,其固联的动坐标系相对惯性坐标系所发生的旋转可以用旋转矩阵R进行表征,且其为(3×3)特殊正交矩阵,即R∈SO(3)={R∈ℜ3×3:RR T=E,detR=1},式中:E—单位矩阵。由Euler旋转定理可知,对于任意位姿矩阵R∈SO(3),可等效于绕固定轴ω={ωx,ωy,ωz}T∈R3旋转一定角度θ,其中,||ω||=1,θ∈[0,2π)。进而,物体在空间的旋转可以用Rodrigues旋转公式的旋量指数积形式,将R表征为ω与θ的函数:
在刚体旋转运动的基础上,进一步考虑刚体一般运动。由Chasles定理可知,三维空间中任s意的刚体运动均可视作为该刚体绕某一轴线的旋转与沿该轴的平移的合成的有限螺旋运动,具体表现[13],如图1所示。其中,A为惯性系,B为动系统,而B的位形空间为R3与SO(3)的乘积空间,记为SE(3)={(p,R):p∈R3,R∈SO(3)}=R3×SO(3)。其中,p为A原点到B原点的位置矢量,B相对于A的旋转矩阵为R。旋量理论中运用SE(3)中的一元素来表示某一特定的刚体运动,即有限螺旋运动。
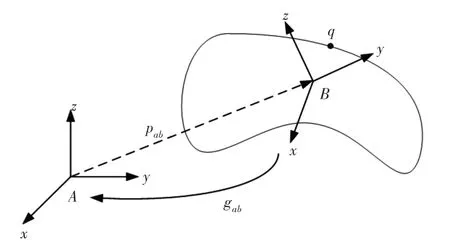
图1 一般刚体运动示意图Fig.1 General Rigid Motion
广义的有限螺旋运动在空间中的运动,如图2所示。根据运动合成原理可以视作为,先由点1旋转至点2,后由点2移动到点3。即广义的旋量运动为绕轴线ω所做的旋转与沿轴线ω移动的合成,其具体可用旋量坐标ξ来表示旋量运动,即可由一对三维向量构成的六维向量表示,具体为ξ=[ν,ω]T∈R6,其中,ν=-ω×q。其反对称阵旋量可表示为:
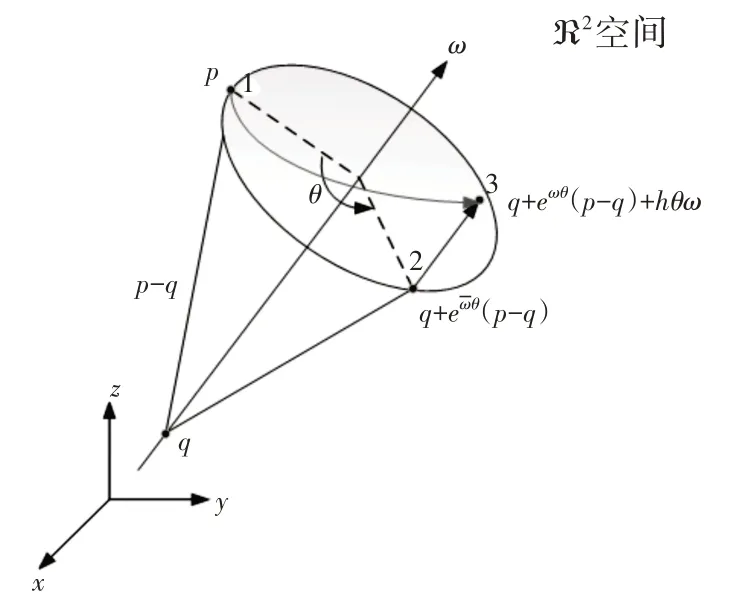
图2 广义有限螺旋运动示意图Fig.2 Generalized Finite Screw Motion
并且为了衡量旋量运动的平移运动与转动的比值,引入了节距h,具体为:
且文献[14]指出,运动旋量与θ乘积的矩阵指数可以表征任意刚体变换,即,具体可以表示为:
2.1 运用旋量理论的机械臂正运动学表示
机构的运动副所蕴含的受约束的运动,是使机构能够形成特定运动的基本条件[15]。对于由n个R副构成的开式串联机械臂,其是由刚性连杆间通过R副耦合串接而成,而每个R副又起到将相邻的各个连杆之间的运动限制于SE(3)的子群之中。对于机械臂的每一关节臂在三维空间中的运动均可用特殊群SE(3)来表征。从本质而言,机械臂的运动是由多个R副所在的关节轴线的运动旋量耦合而成。对于某一关节上的运动旋量,则沿此运动旋量轴线连杆的刚体运动可以表示为:
式中:gab(0)—运动过程中连杆的初始位形;
gab(Θ)—运动过程中连杆的最终位形;
Θ—关节空间,即:
文献[14]指出,刚体空间运动SE(3)可以通过se(3)的指数变换来表征,即机械臂中的各个连杆之间的刚体变换可写作为某个运动旋量的指数形式,即gst:Q→SE(3)。因此由Euler 定理及Chasles定理可知,空间中机械臂的空间运动可以视作为为各个关节旋转群的正则坐标的耦合,具体的开链机构的总运动方程可以表示为:
上式即机械臂正运动学的指数积公式。
2.2 运用旋量理论的机械臂逆运动学表示
2.2.1 Paden-Kahan子问题的描述
在运用旋量理论对机械臂的逆运动进行求解时,常将运动旋量视作为几何体,并在旋量指数积所构建出的正解基础上,运用几何方法将原先较为复杂的逆解问题分解为多个连续的子问题进行求逆。学者Paden 与学者Kahan 一同总结出了三种典型的运用几何方法对运动旋量指数积求逆解的子问题,而这些具备着明确几何意义且可用旋量指数积能够明确表示的求逆问题统称为Paden-Kahan 子问题。这里列出了两位学者所总结出的这三种经典的Paden-Kahan 子问题的具体问题描述及几何表示[14],如表2所示。
相关文献表明,Paden-Kahan第二子问题为解决以多R副构成串联机械臂的关键[10-12]。故此,对于子问题1与子问题3,对这里暂且不进行详细讨论。
2.2.2 Paden-Kahan第二子问题求解
Paden-Kahan第二子问题,指对刚体绕两个已确定了几何关系的定轴依次进行有序的旋转后的运动进行逆运动学求解,其具体的几何描述,如表2所示。文献[5]已给出了Paden-Kahan的第二经典子问题具体的解法。当ω1×ω2≠o时,即两定轴轴线不平行时,设有如下矢量:
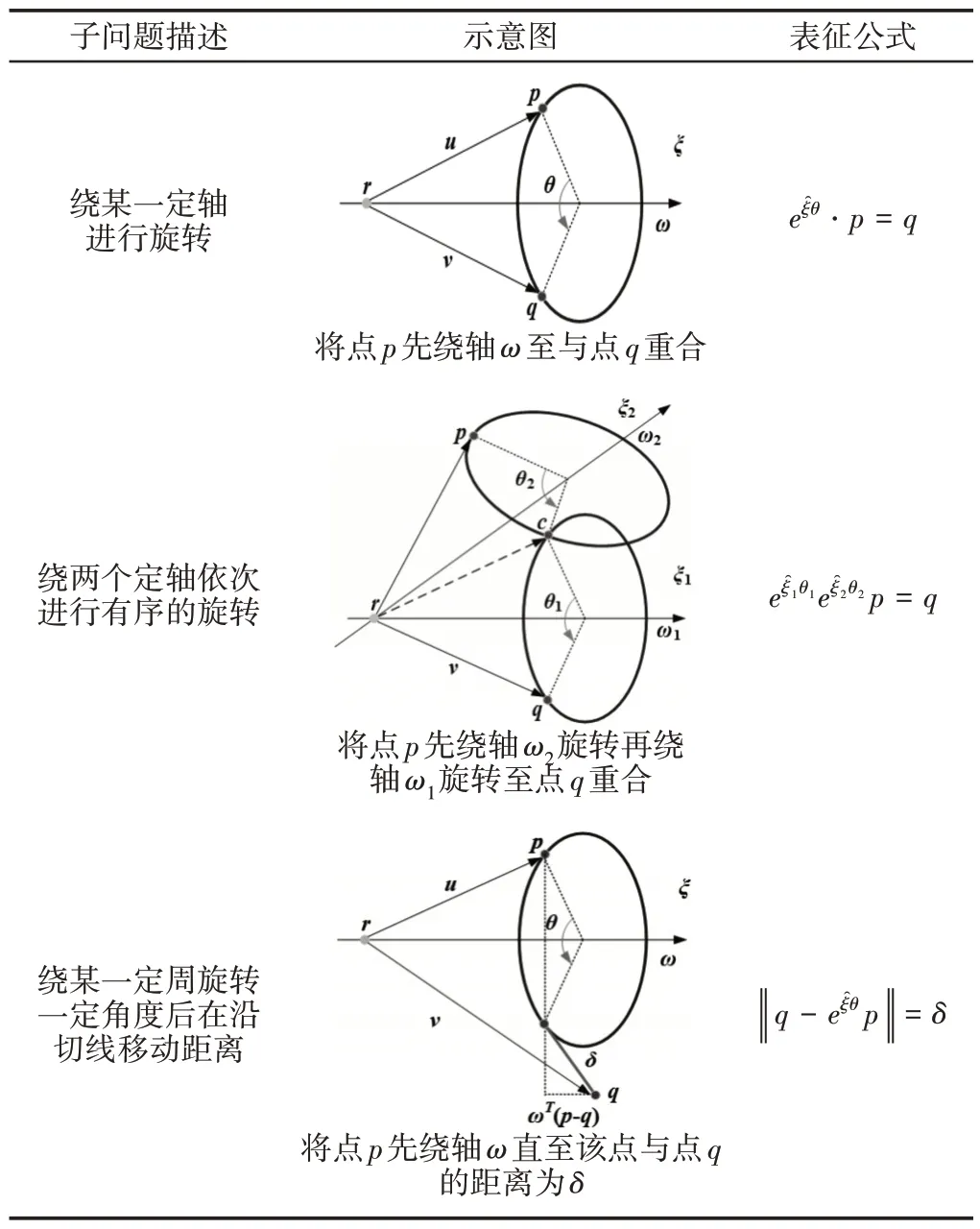
表2 Paden-Kahan子问题Tab.2 Paden-Kahan Subproblems
进一步求得θ1与θ2有:
值得注意的是,当表示旋量的螺旋的两个圆之间有两个交点时,式(11)有2组解;两圆有一个交点时,式(11)有1组解;当两圆不相交时,无解。而当ω1×ω2=o时,即两轴线平行时,则有:
并设有:
则有:
2.2.3 Paden-Kahan第二子问题的扩展问题
Paden-Kahan第二子问题解决了刚体绕两个已确定了几何关系的定轴进行有序的旋转的逆解。但对多R副构成串联机械臂进行求逆时,即对多个连续的第二子问题进行求逆时,易因R副轴线的几何关系不确定,即Paden-Kahan第二子问题所绕定轴间的几何关系不确定,而产生求逆解的困难。这里在第二子问题的基础上进行了扩展,旨在简化第二子问题求机械臂逆解的过程。其问题可描述为绕若干个无确定几何关系的定轴依次进行有序的旋转的逆解问题,其几何描述,如图3所示。
下面将对算例进行求解说明,算例具体情形,如图3 所示。显然,图示问题为Paden-Kahan 第二子问题的衍化,其中ξ2与ξ3的轴线相互平行,即ω3×ω2=o;而ξ1则与其余两旋量呈现非平行的任意角度,且此问题可由下式进行表征:
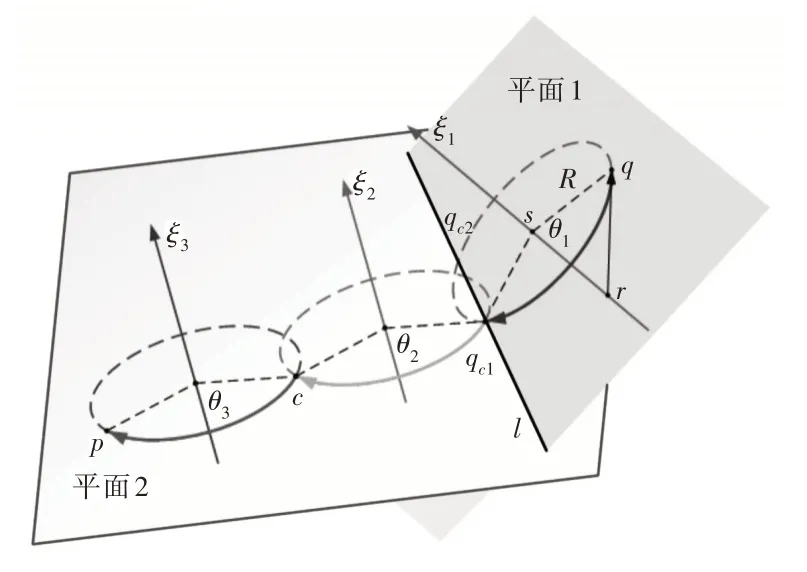
图3 Paden-Kahan第二子问题扩展问题图示Fig.3 The Extension Problem of the Second Paden-Kahan Problem
q点在旋量ξ1上的投影s为:
式中:r—旋量ξ1轴线上的任意一点。
几何上直观,逆运动学是否有逆解取决于各个表征旋量的螺旋的圆之间是否有交点,而表征旋量的圆的半径可由下式表征:
而是否有交点qc则可由几何方法进行确定,具体的判别式D为:
点qc的取值与D有关,即:
通过点qc的确定,即θ1可通过子问题1进行求解,即有如下:
θ2与θ3则可按第二子问题两旋转轴平行进行处理,即:
根据式(12)~式(14)进行求解。特别注意的是,当D>0时,qc存在2个解,需分别代入上式进行两次求解,并根据具体的旋量大小进行取舍。
3 ABB IRB2600型机器臂逆运动学构建
为验证这里所提出的Paden-Kahan第二子问题的扩展问题求解的正确性,这里以ABB公司的IRB2600型机械臂作为验证对象,下面将以旋量指数积原理并结合Paden-Kahan第二子问题及其扩展问题,对机械臂的正逆运动学进行求解。IRB2600型机械臂为典型的6R机械臂,即可通过6个旋转副(R副)实现空间运动。该型机械臂的拓扑结构可表示为SOC{-R1⊥R2∥R3⊥R4⊥R5⊥R6-},其中⊥与∥分别表示2个旋转关节轴线的垂直与平行,具体的各个关节的轴线的空间位置关系,如图4(a)所示。
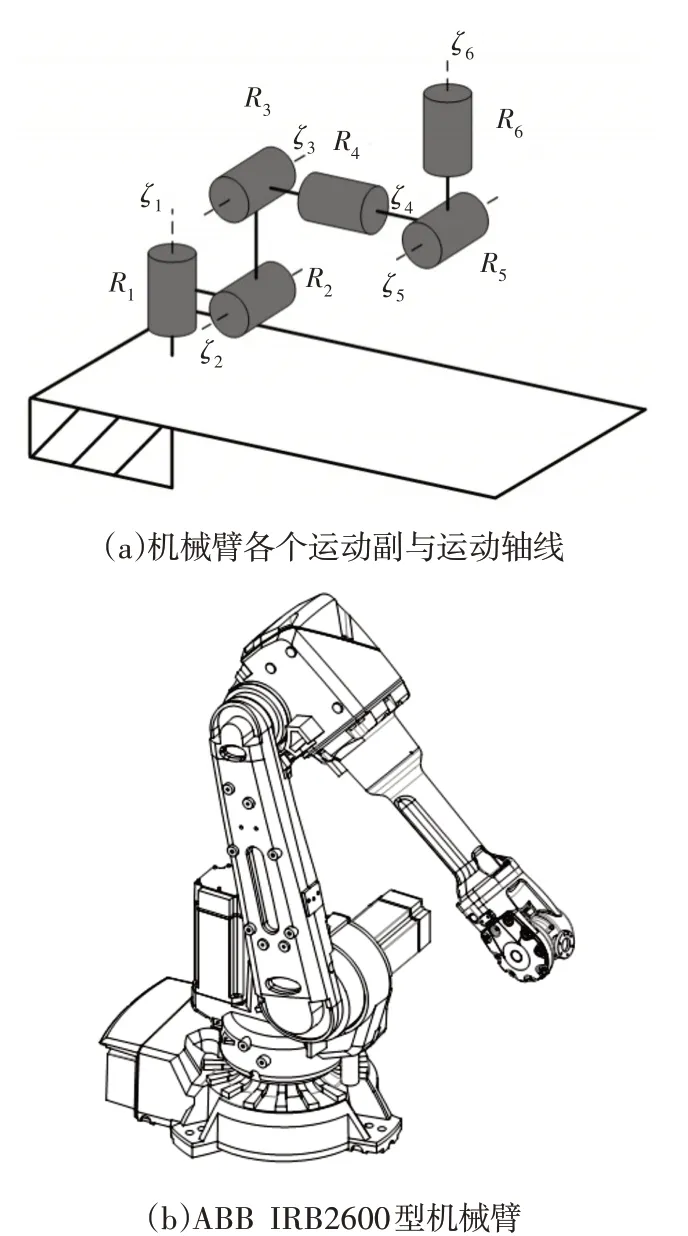
图4 ABB IRB2600型机械臂及其各个关节运动轴线Fig.4 ABB IRB2600 Robot and its All Ankle Axes
构造出机械臂各个R副所在关节的运动旋量,具体为:
并考虑机械臂的几何参数,得到各个关节所在的旋量为:
由上文所述,6R机械臂的正解公式为:
由于末端执行器所在点q6,位于4、5与6的轴线交接点上,设(4×4)方阵T为机械臂末端执行器的姿态矩阵,并考虑到式(10)与gab(θ)=T后则有:
θ4与θ5可由Paden-Kahan第二子问题通过下式进行求解:
θ6则根据Paden-Kahan第一子问题通过下式进行求解:
以上θ1、θ2、θ3、θ4、θ5与θ6均得到求解。
4 实验与分析
根据ABB 公司的IRB2600产品说明书,得到其具体的D-H参数,如表3所示。
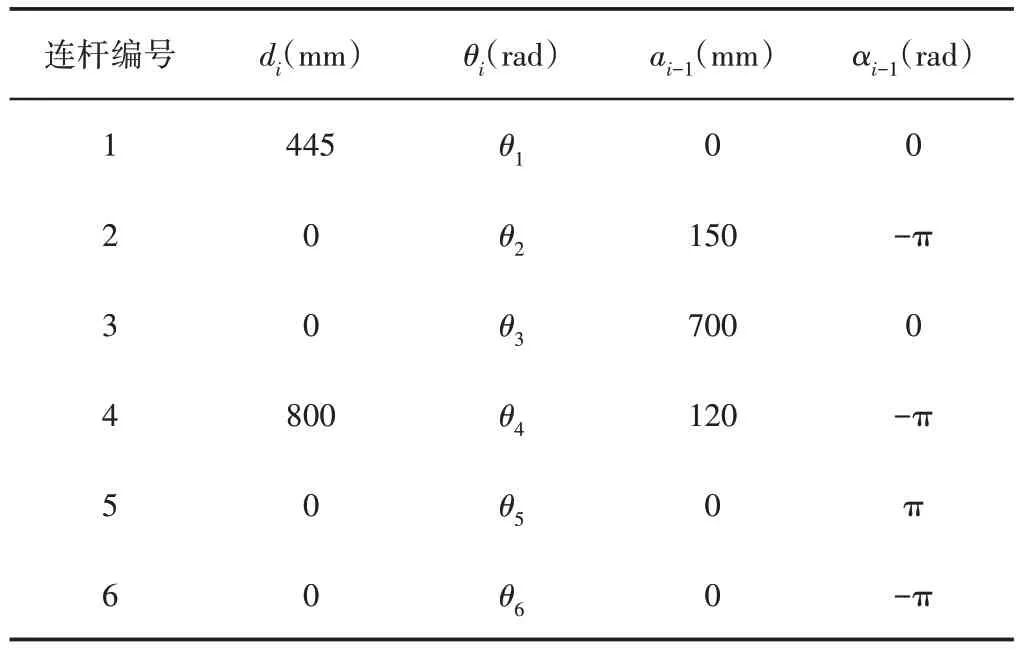
表3 这里所用ABB IRB2600型机器臂D-H 参数Tab.3 D-H Parameters of ABB IRB2600 Robot
并取Θ的各个元素的数值为:
并由正运动学计算出机械臂末端执行器的位姿矩阵T为:
并以所计算出的位姿矩阵T作为逆运动学的求解目标,运用旋量理论并考虑了Paden-Kahan第二子问题的扩展问题,构建出了ABB IRB2600型逆解公式后,运用Matlab 软件求得六组逆解值,如表4所示。在得到以上六组逆解后,再分别重新代入正运动学公式进行求解。分析结果可知,所有的逆解均未出现无解情况,且所有解均在机械臂的有效工作空间之中;并且所有的六组逆解代回正解公式后,均近似到达了式(25)所列出的位姿,其中方向偏差最大为(6.8×10-12),最大位置偏差为(1.2×10-10)mm。由此验证了这里提出的Paden-Kahan第二子问题的扩展问题在串联机械臂逆运动学求解方面应用的有效性。
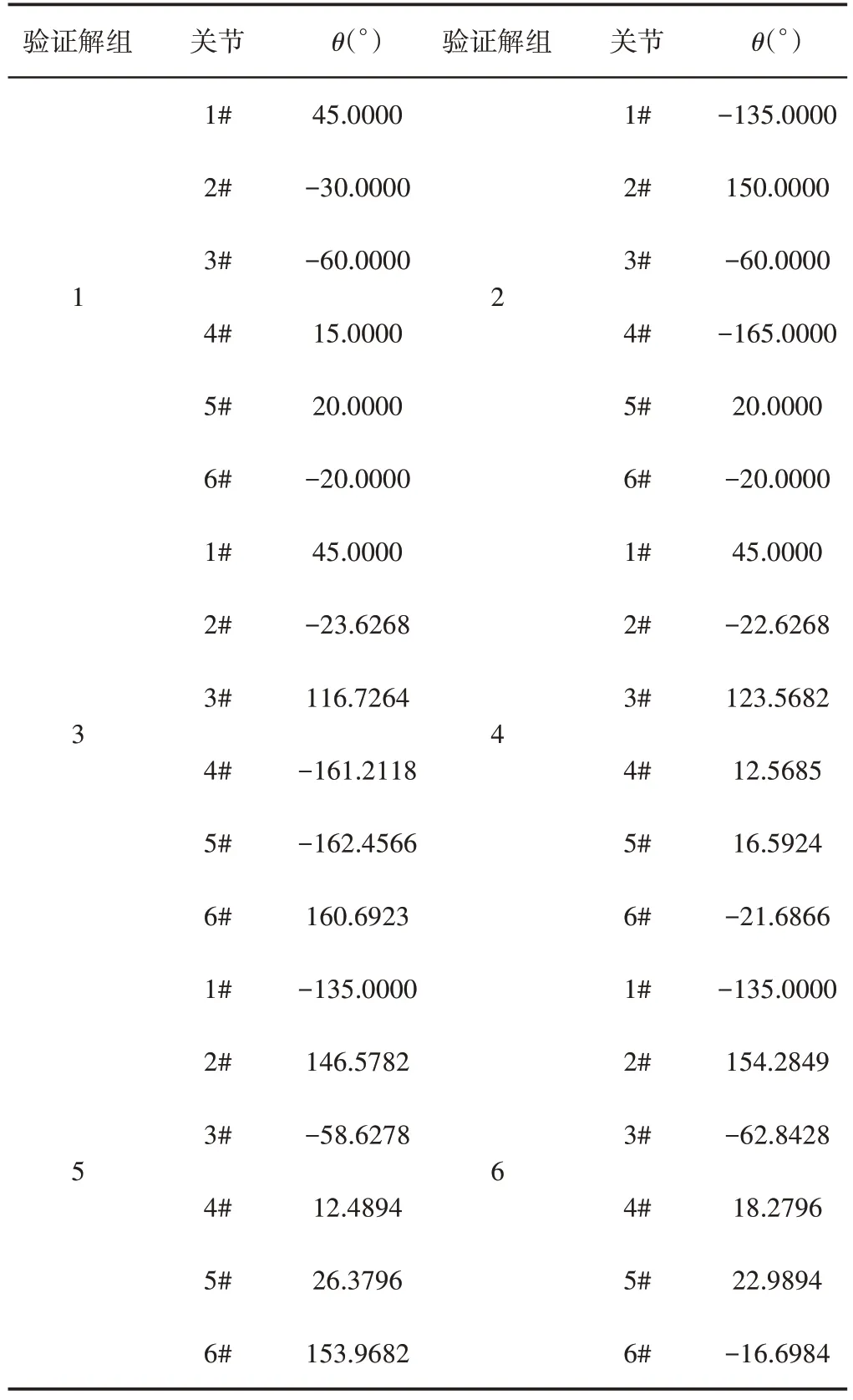
表4 六组运用Paden-Kahan第二子问题的扩展问题进行求解后的逆解值Tab.4 Six Inverse Solutions by the Second Paden-Kahan Subproblems
5 结论
(1)运用旋量理论实现了机械臂正运动学的指数积公式的构建;(2)提出了Paden-Kahan第二子问题的扩展问题,即绕若干个无确定几何关系的定轴依次进行有序的旋转的逆解问题的求解方法;(3)以ABB IRB2600型机械臂作为验证对象,通过第二子问题的一种新的扩展问题对其进行求逆运算,在经过对6组解验证后,验证了这里提出的Paden-Kahan第二子问题的扩展问题在串联机械臂逆运动学求解方面应用的有效性。
