线性回归模型偏F检验与t检验等价性的一种证明方法

卢跃奇

(洛阳师范学院 数学科学学院,河南 洛阳 471934)

1 线性回归模型偏F检验与t检验等价性原理

经典均值线性回归理论模型的一般形式[1]为

y=β0+β1x1+β2x2+…+βpxp+,

等价的样本形式为

yi=β0+β1xi1+β2xi2+…+βpxip+i,

(1)

设估计参数β所需的n个训练样本为(xi1,xi2,…,xip;yi),i=1,2,…,n,这些样本可表述为自变量观测值构成的n×(p+1)设计矩阵

和因变量观测值构成的向量Y=(y1,y2,…,yn)′,其中1n=(1,1,…,1)′表示元素全为1的n维列向量,Xj=(x1j,x2j,…,xnj)′表示变量xj在n次观测中的取值,x′i=(1,xi1,xi2,…,xip)表示第i个样本中所有自变量(包括截距项)的观测值。

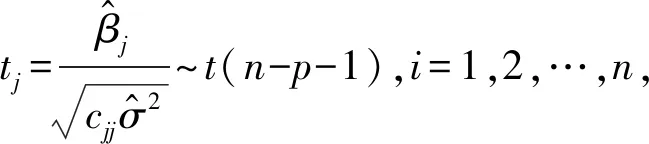
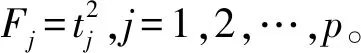
2 偏F检验与t检验等价性的证明

注意到

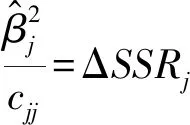
调整线性回归模型(1)中变量的顺序,把变量xj调整到第一个位置,从而模型改写为

yi=βjxij+β0+β1xi1+β2xi2+…+βj-1xi,j-1+βj+1xi,j+1+…+βpxip+i,

(2)

由于只是改变了模型中变量的先后顺序,模型本身不变,所以本质上模型(2)和原模型(1)完全等价,即参数的极大似然估计和显著性检验统计量等都保持不变。模型(2)的设计矩阵仍记为X=(Xj,1n,X1,X2,…,Xj-1,Xj+1,…,Xn)=(Xj,X-j),其中X-j表示从p元线性回归模型(2)移除变量xj后的p-1元线性回归模型

yi=β0+β1xi1+β2xi2+…+βj-1xi,j-1+βj+1xi,j+1+…+βpxip+i

(3)

的设计矩阵。

为叙述方便,不失一般性,下面以j=1为例证明偏F检验与t检验的等价性。

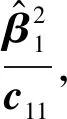
X=(X1,X-1),

从而

利用分块矩阵逆的一般表示形式(分块矩阵的逆有很多形式,此处取其形式之一,其中要求D和A-BD-1E可逆)[3],

记H=X(X′X)-1X′,H-1=X-1(X′-1X-1)-1X′-1,分别表示模型(2)和模型(3)的帽子矩阵[4-7]。

记In表示n阶单位阵,则

其中

c11=(X′1X1-X′1X-1(X′-1X-1)-1X′-1X1)-1=(X′1(In-H-1)X1)-1。

由于

故

从而

2)考虑ΔSSR1,注意到帽子矩阵H可表示为

X1c11X′1-H-1X1c11X′1-X1c11X′1H-1+H-1+H-1X1c11X′1H-1=(In-H-1)X1c11X′1(In-H-1)+H-1。

同时,注意到模型(2)的回归平方和可以表示为

从而,模型(2)与模型(3)的回归平方和之差ΔSSR1为

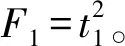
3 结束语

对经典的均值线性回归模型中的变量进行统计显著性检验,是应用线性回归模型之前的必须步骤。为了逐个检验线性回归模型中每个自变量对因变量影响程度的统计显著性,可使用偏F统计量和t统计量进行分析,不同的统计软件可能会使用不同的检验统计量进行计算,给出不同的结果,但其中给出的p值总是相同的,即本质上这两种检验是等价的。本文给出的证明偏F检验与t检验等价的分块矩阵方法,原理简单易懂,特别适合于课堂教学和学生自学,为相应的回归分析课程教学提供一种思路和方法。