基于微波热声层析成像定量重建生物组织电导率的改进方法*
2023-02-26陈艺迟子惠吴丹刘悦温艳婷李伦蒋华北
陈艺 迟子惠 吴丹 刘悦 温艳婷 李伦 蒋华北
(1)重庆邮电大学计算机科学与技术学院,重庆 400065;2)重庆邮电大学光电工程学院,重庆 400065;3)成都市第五人民医院超声医学科,成都 611130;4)Department of Medical Engineering,University of South Florida,Tampa 33620,USA)
用于疾病诊断的传统医学影像技术有X射线成像技术(X-ray)、计算机断层扫描技术(computed tomography,CT)、核磁共振成像技术(magnetic resonance imaging,MRI)以及超声成像技术(ultrasound imaging,UI)等。每一种医学影像技术都有其适用的应用场景,也存在各自的局限性。比如X-ray和CT[1-2]都会对人体产生电离辐射,UI和MRI[3-5]虽然无电离辐射,但是UI的对比度差、MRI时间分辨率不高且价格昂贵。近年来,在新型生物影像技术中,微波热声层析成像(microwaveinduced thermoacoustic tomography,MTAT)技术因其独特的优势而受到众多国内外研究人员的青睐。
MTAT是一种混合医学成像方式,它结合了超声成像高分辨率和微波成像高对比度的优点[6-7],已被用于乳腺、脑、关节、血管[8-12]等组织器官的检测。当微波信号辐射到待测生物组织时,生物组织吸收微波能量温度升高而产生热弹性形变,向外产生热致超声波信号,可以通过分布在生物组织周围的超声换能器接收,处理该信号可得到高分辨率和高对比度生物组织的图像信息[13-14]。其中组织图像中呈现的高对比度是某种电磁参数的对比度,如生物组织的电导率、介电常数等。有研究表明,离体恶性乳腺组织在微波频率下的电导率是正常组织的6 倍左右[15]。并且有文献提到,生物组织功能性信息比如水含量、血红蛋白浓度等,都是直接与组织的电导率有关[16],因而可以通过电导率这一电磁参数来为准确评估生物病变组织及其生理特性提供重要依据。
目前,在生物组织重建分析的算法方面大部分研究团队采用的是基于传统MTAT技术的定性成像算法,如延迟叠加算法、反投影重建法和时间反转算法等[17-20]。由于微波在生物组织中的分布高度不均匀[21],导致这些定性算法重构的吸收微波能量密度不能定量地表征电导率等电磁特性的分布。除此之外,国内电子科技大学赵志钦课题组[22-23]针对乳腺肿瘤检测提出的基于压缩感知的重建算法,主要重建的是生物组织的声压、声速分布等。中国科学院电工研究所的刘国强团队[24]将注入电流式热声成像方法应用于复杂生物组织结构中,通过猪肝仿体实验得到声压波形来反映仿体电导率变化的位置。虽然这些重建算法都能用于病变组织的检测分析,但无法定量获得组织的电导率来表征生物组织特性。Guillaume Bal等[25]在2011 年对MTAT 进行定量分析研究,他们把MTAT算法分为两步,第一步根据检测到的热声信号重建出吸收能量密度,第二步求解麦克斯方程组重建电导率。但是该团队给出的相关算法仅在数值模拟中验证了算法的可行性,并未在实验中验证其可行性。Paul Beard 团队[26]在2012 年将CST 仿真软件与MATLAB 结合进行混合编程,把CST仿真软件得到的电场分布,代入到计算得到的吸收分布中从而获得电导率分布,同样他们也只是通过数值模拟验证实验。而蒋华北课题组[27]于2010 年最早提出和发展了MTAT定量重建电导率的思想和算法,并进一步从实验上验证了该定量算法在乳腺癌MTAT 的可行性[28-29]。他们提出的定量MTAT 算法[27]证明了通过基于有限元的重建算法与亥姆霍兹方程结合可以获得电导率分布,但是其电导率的获得过程采用的是拟合(fitting)的方法,即最小二乘法的拟合,通过寻找吸收能量密度的测量值与观测值之差的平方和。该方法泛化能力不够好,算法的稳定性以及电导率的重建精度都有待进一步提高。算法越稳定、重建精度越高,对于乳腺肿瘤等疾病的早期定位和分期的精准筛查与监控,预防疾病恶性的发展具有重要意义。因而本研究采用基于正则化牛顿迭代法(regularized Newton iteration method,RNIM)定量重建电导率,将定量MTAT方法中获得的吸收能量密度作为先验性信息来规范解,改善变量条件使获得的重建值精度提高。
本文内容依次包括:第1节详细介绍改进的重建方法以及仿体实验所涉及的系统;第2节采用改进的方法和fitting方法进行多组数值模拟实验,验证改进方法的有效性,并在多组仿体实验中,对比分析两种方法的重建结果并讨论了改进的方法的优越性;第3节给出研究结论,并指出研究工作中的不足之处,以及对下一步研究工作的展望。
1 材料与方法
1.1 定量重建电导率的方法
本文采用的基于RNIM重建电导率的过程主要分为以下两步。第一步采用有限元离散法求解热声波动方程,获得吸收能量密度φ。其核心过程是根据蒋华北课题组研究的基于模型的迭代重建算法[27,30-31]。其主要公式如下:
在公式(1)中:p(r,t)为t时刻位于r处产生的声压;C为声速,一般在生物软组织中的传播速度约为1 500 m/s;βe为体积膨胀系数;Cp为比热容;φ(r)为吸收能量密度;J(t)=δ(t-t0)为假定t时刻的微波脉冲函数。在公式(2)中,J为边界上测得的声压值对吸收能量密度的偏导数组成的雅克比矩阵;Po为真实的声压分布;Pc为通过给定的初始吸收能量密度正向求解获得;Δφ=(Δφ1,Δφ2,…,Δφn)T为吸收能量密度的更新矢量;I为单位矩阵;λ'为正则化参数。
第二步采用Tikhonov 正则化方法在给定初始电导率的条件,利用第一步获得的吸收能量密度φ直接更新/重建电导率。求解过程如下:
利用Tikhonov 正则化建立1 个加权项和1 个惩罚项,使得φo与φc之间的平方差最小化。
其 中:σ0为电导率的初始值;φo=(φ1o,φ2o,…,φNo)T为对微波热声波动方程式(1)进行有限元离散获得的吸收能量密度分布,N为图像重建域中的节点数;φc=(φ1c,φ2c,…φNc)T为通过公式(4)求得的吸收能量密度分布。
其中Es(r)为电场强度,通过求解亥姆霍兹方程(9)获得。
λ为Marquardt-Tikhonov 正则化参数,在本文中取值为时,惩罚项随着误差变化,重建效果最佳。其中trace(·)表示矩阵的迹,误差函数定义为:
基于牛顿迭代算法更新电导率σ:
其中:Δσ为电导率σ的更新矢量;J为吸收能量密度对电导率的偏导数组成的雅克比矩阵,
其中k=1,2,3,…,N,j=1,2,3,…,N均表示求解域中的结点个数。特别地,雅克比矩阵J的矩阵元素由下式决定:
对于其中的总场Es通过下式亥姆霍兹方程求得:
入侵是指外界对计算机,互联网,信息系统的破坏性,使其完整性,安全性受到外部活动侵入,而如今,检测是指特殊部门能够利用多种方法识别不法行为,通过收集内外部的活动数据和识别活动行为,来对计算机的整个活动进行分析,识别异常行为。入侵检测系统是能够利用数据分析识别计算机网络系统异常行为,针对所识别出来的异常活动数据进行检测,包括内外部一些用户的行为数据解析,利用这种入侵检测系统能够实时监测到网络运行系统的用户行为,并针对这些异常行为采取有效措施,极大程度控制异常状况。
其中:μr为相对磁导率,在生物组织中视为定值;εr为等效介电常数;k为波数。对方程(9)进行有限元离散化后可表示为[27]:
基于方程(10),公式(8)中的吸收能量密度对电导率的偏导数可通过对下式采用基于伴随灵敏度法[32]获得:
具体采用RNIM方法求解电导率的算法流程如图1 所示。相比fitting 方法求解电导率,改进的方法将获得的吸收能量密度作为先验信息加入到重建模型,改善了变量条件,使得到的解稳定性提高,并在实验结果与讨论部分通过组织仿体实验进行验证。

Fig.1 Algorithm flowchart
1.2 实验系统
本文采用单通道热声成像系统来完成仿体实验(图2)。采用S波段(中心频率为3 GHz的微波源,脉宽为550 ns)产生脉冲微波。实验中通过标准角锥喇叭天线(孔径:114 mm×114 mm,增益:10 dB)将微波能量辐射到浸没在耦合剂——变压器油中的样品上,样品吸收微波能量产生热声信号。产生的热声信号被超声换能器(中心频率:2.25 MHz,晶体直径:12 mm)探测,经过低噪放大器(带宽:260 kHz~2.2 MHz,放大倍数:58 dB)后,被50 MHz 采样率的采集卡采集。在本实验中,采用的是超声换能器侧向圆形扫描,采集360°范围内的热声信号用于图像重建。
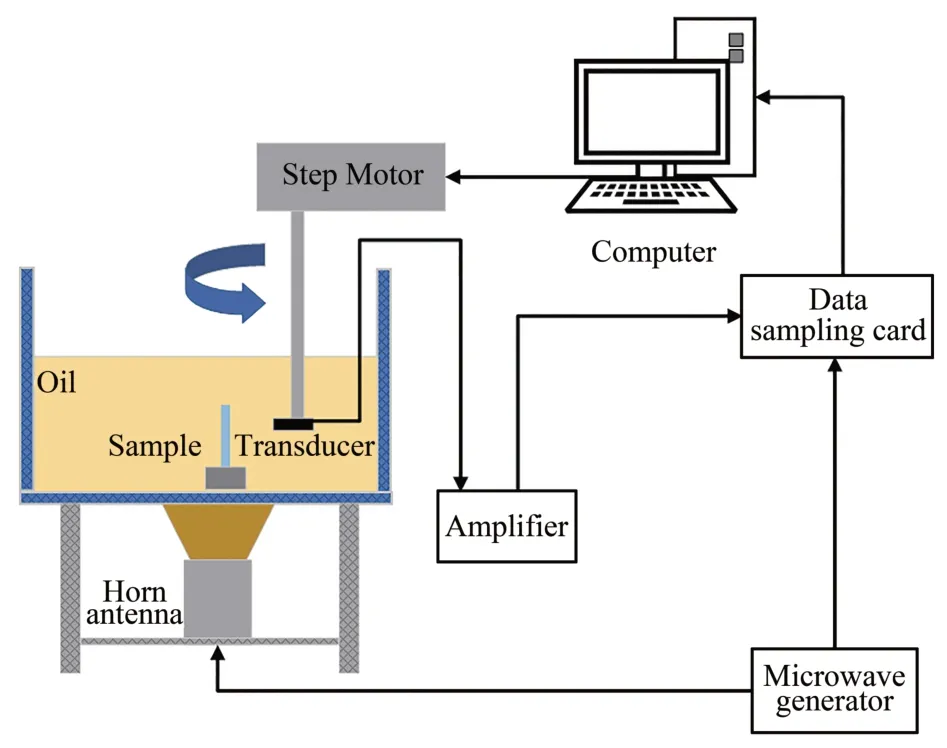
Fig.2 Schematic of the experimental setup
2 结果与讨论
2.1 数值模拟实验
为验证改进方法的有效性,本文共设计两组数值模拟实验,分别为单目标的电导率重建和不同形状不同对比度的多目标的电导率重建,其中通过给定的初始电导率正向求解获得每组模拟实验用到的测量数据。在数值模拟实验中采用有限元双网格理论[33-34]进行定量重建,所用节点数为1 584~6 153。仿真实验涉及的主要参数为:相对磁导率μr=1.0 H/m,真空介电常数ε0=8.854×10-12F/m,相对介电常数εr=71 F/m,初始电导率σ0=0.001 S/m,微波频率f=3.0×109Hz以及在直径为40 mm的圆形区域设定背景电导率σ=0.1 S/m。仿真实验结果在CPU为2.30GHz,内存为32GB的PC机中的MATLAB上运行得到。
图3 给出了单个圆形目标的电导率重建图像,目标直径10 mm 电导率为0.2 S/m。图3a 为真实的电导率分布图像,图3b,c 分别为采用RNIM 方法和fitting方法重建的电导率分布图像,并在图3d中绘制了经过目标中心y=0 mm的剖面曲线,两种方法重建结果与真实的电导率分布情况完全吻合。

Fig.3 Reconstructed conductivity images for a single circular target
为验证RNIM方法对不同形状不同对比度目标的重建能力,图4 给出了对应电导率的重建图像,其中正方形、椭圆、圆形目标的电导率分别为 0.4、0.3、0.2 S/m。图4a-c分别为真实的电导率分布图像、采用RNIM 方法和fitting 方法重建的电导率分布图像。同样,为了验证RNIM 方法的有效性,在图4d,e 中绘制了经过目标在y=5 mm 和y=-10 mm 的剖面曲线,结果显示两种方法都能精准重建目标电导率。

Fig.4 Reconstructed conductivity images for three targets having different shapes and contrast
通过以上两组数值模拟实验结果显示,采用RNIM方法能准确地定量重建单目标的电导率以及不同形状不同对比度的多目标的电导率,证明了RNIM方法的有效性。为了进一步验证RNIM方法的优越性,设计了4 组具有代表性的组织仿体实验。实验对象为不同浓度的NaCl 溶液,具有不同的电磁参数。其中具体的电磁参数值是通过Debye模型[35]计算得到。仿体实验采用变压器油作为实验背景,其相对介电常数为2,电导率为0.001 S/m。
2.2 仿体实验
第一组实验为在单根直径为3 mm的塑料管内装入浓度为1.18%的NaCl 溶液,相对介电常数为73.4,电导率为2.06 S/m,放置在不同位置的图像重构。采用两种方法分别定量重建电导率,结果如图5 所示。第一列图5a,d,g,j为1~4号不同位置的仿体采用fitting 方法的重建图,中间列图5b,e,h,k为1~4号不同位置的仿体采用RNIM 方法的重建图,最右边列图5c,f,i,l 为分别采用两种方法沿仿体中心的电导率曲线和真实值的比较图,为了凸显分别采用两种方法重建电导率的差异,重点选取曲线上方部分进行放大显示。从图中很直观地看出采用RNIM方法重建的电导率更接近真实值,对应的电导率定量重建分析结果如表1所示。结果显示,相同大小相同浓度的单目标放在不同位置,采用fitting 方法重建的目标电导率值在1.95~2.12 S/m范围浮动,而采用RNIM方法重建的电导率值在2.02~2.06 S/m 范围浮动,与真实值更加接近,并且由图6表明采用RNIM方法重建不同位置的电导率变化幅度小,稳定性更高。采用FWHM(半高宽)的方式测量重建目标的尺寸,得到采用RNIM方法重建大小范围为 2.35~3.09 mm,采用fitting 方法重建大小范围为2.20~3.08 mm,采用RNIM和fitting方法重建目标的大小均接近真实值。定量重建仿体目标的形状、尺寸与真实目标的特征属性吻合较好。

Fig.5 Reconstructed conductivity images of the single target at different positions
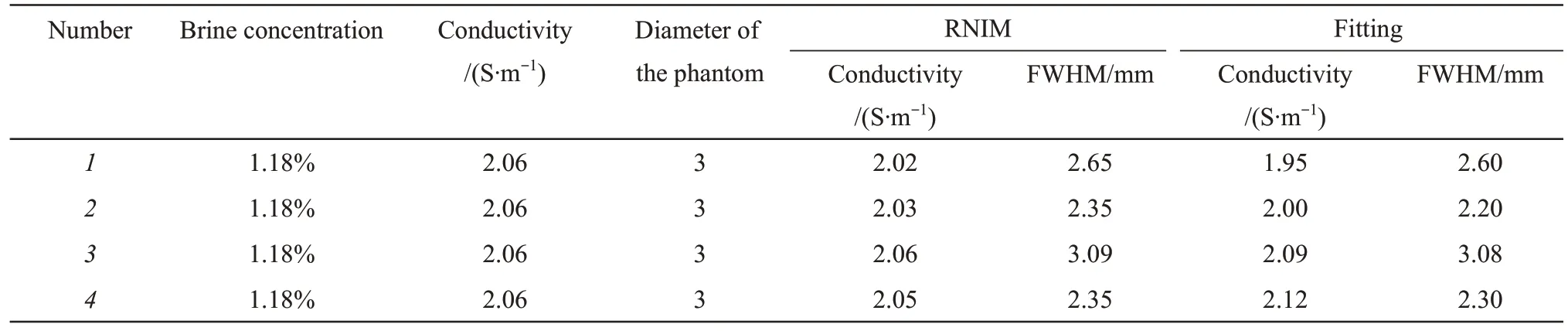
Table 1 Comparison of quantitative reconstruction of single target conductivity at different positions using two methods separately
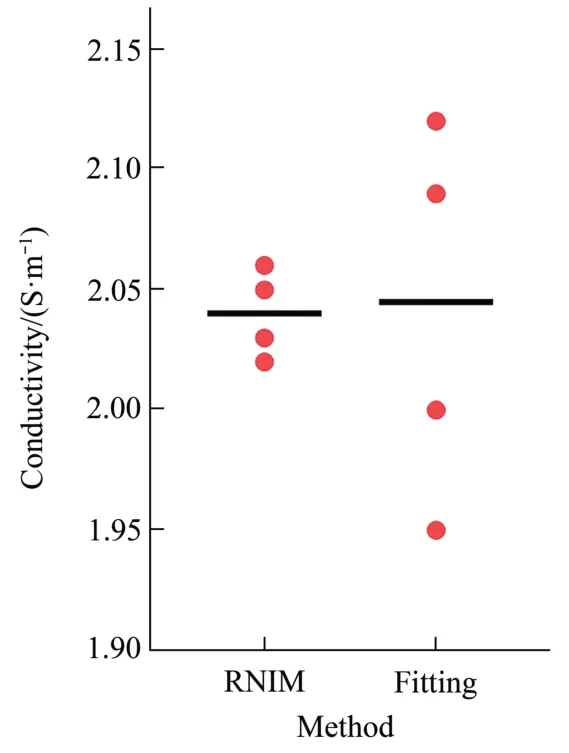
Fig.6 Comparison of single-target conductivity reconstruction values
通过平均相对误差这一指标,对两种方法重建电导率的能力进一步进行定量对比分析,具体计算如下式(12)所示。
其中,n为单目标实验次数,σR为目标电导率的重建值,σT为目标电导率的真实值。采用RNIM方法重建不同位置的电导率的平均相对误差从3.15%降低到0.98%(表1)。从实验结果来看,采用RNIM方法定量重建相同电导率的仿体,在不同位置的准确度显著提高,这对于早期肿瘤的定位和分期的精准诊断具有重要意义。
第二组实验为不同盐水浓度的单目标仿体,在单根直径为3 mm 的塑料管内装入1 号仿体浓度为2%的NaCl溶液,相对介电常数为71.8,电导率为3.34 S/m,2号仿体浓度为3%的NaCl 溶液,相对介电常数为70,电导率为4.81 S/m。通过不同盐水浓度的仿体电导率重建实验,验证了本文改进方法的优越性,对浓度因素的良好泛化性。具体地,采用盐水浓度1.18%的第3号数据作为训练数据,对fitting 方法和RNIM 方法中的初始参数进行校准,重建未知的不同盐水浓度的单目标仿体电导率。结果如图7所示,第1列为采用fitting方法的重建图,中间列为采用RNIM方法的重建图,最右边列为分别采用两种方法沿仿体中心的电导率曲线和真实值的比较图,同样重点选取曲线上方部分进行放大显示,具体对应的电导率定量重建分析结果如表2所示。分别采用两种方法重建1号和2号仿体的FWHM,RNIM 方法重建仿体的FWHM 分别为 2.40 mm 和2.36 mm,fitting 方法重建仿体的FWHM值分别为2.34 mm和2.30 mm,两种方法重建目标的大小均接近真实值。通过相对误差这一指标,对重建结果进一步进行定量分析,结果显示1号仿体采用RNIM 方法重建电导率相对误差为2.10%,采用fitting 方法重建电导率相对误差为9.88%。同理,2号仿体采用RNIM 方法重建电导率相对误差为3.74%,采用fitting 方法重建电导率相对误差为9.36%。比较相对误差结果发现,相比于fitting 方法,采用RNIM 方法重建未知不同浓度的仿体电导率的相对误差更低,泛化能力更好。
虽然采用RNIM 方法相比fitting 方法得到电导率的重建用时稍长些,在CPU 为2.30 GHz,内存为32 GB PC 机中的MATLAB 上运行,采用RNIM方法重建电导率约用时约为47 min,采用fitting方法重建电导率用时约为44 min。但是在肿瘤的定位和分期的早期筛查及精准诊疗中,电导率的重建精度比重建效率更重要。预防疾病恶性的发展,达到肿瘤的早发现早治疗,减少病死率,延缓肿瘤患者生存期限。

Fig.7 Reconstructed conductivity images of the single target at different concentrations

Table 2 Comparison of quantitative reconstruction of single target conductivity at different concentration using two methods separately
2.2.2 多目标仿体实验
第3 组实验是在左边直径为3 mm、右边直径为4 mm 的两根塑料管内分别装入浓度为2%的NaCl 溶液的电导率图像重构,其中相对介电常数为71.8,电导率为3.34 S/m。在本组实验中,设定的对应3 mm和4 mm的目标电导率的对比度为1∶1,定量重建电导率的结果如图8a~d所示。第4组实验是在左边直径为3 mm、右边直径为5 mm的两根塑料管内分别装入浓度为2%相对介电常数为71.8,电导率为3.34 S/m的NaCl溶液和浓度为4%相对介电常数为68.1,电导率为6.21 S/m 的NaCl 溶液的图像重构。在本组实验中,设定对应3 mm和5 mm的目标电导率的对比度约为1∶1.85,定量重建电导率的结果如下图8e~h 所示。第1 行图8a,e 为采用fitting方法的重建图,第2行图8b,f为采用RNIM方法的重建图,第3、4行图8c,g,d,h为采用两种方法分别沿两个仿体中心的电导率曲线和真实值的比较图。同样为了凸显分别采用两种方法重建电导率的差异,重点选取曲线上方部分进行放大显示,从图中仍然可以很直观地看出采用RNIM方法重建的电导率更接近真实值,具体的定量数值分析结果如表3 所示。结合图8c,d 和表3 中的定量分析结果,可以看出在相同浓度下目标大的仿体吸收脉冲能量多,重建的电导率更加接近真实值,并从图8a采用fitting方法重建的电导率结果中明显看出左边目标信号强度大,对比度强于右边目标。但是从图8b 中明显看到左右两边对比度差别不大,并且表3定量分析结果也显示采用RNIM方法重建左右两边目标的电导率都更接近真实值,重建对比度约为1∶1.04,而采用fitting 方法重建对比度约为 1∶1.14。同理结合图8g,h和表3显示采用RNIM方法能更加准确地定量重建仿体的电导率,重建对比度约为1∶1.92,而采用fitting方法重建对比度约为 1∶2.19,定量分析结果表明采用RNIM方法定量重建不同对比度组织仿体的准确度更高。但是需要指出,在图8e~h中仿体直径为3 mm时重建为实心,而仿体直径5 mm时重建出现凹陷现象,原因在于直径大的仿体目标其热声信号的主频低,不在实验采用的超声换能器接收范围内,对于这个问题,在将来的应用中可采用更高带宽的超声换能器。
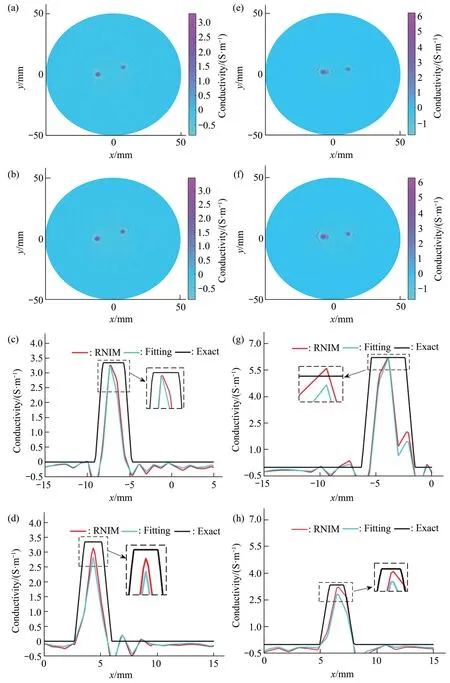
Fig.8 Reconstructed conductivity images of multi-target

Table 3 Comparison of quantitative results of multi-target conductivity reconstruction using two methods separately
通过相对误差这一指标,对重建结果进一步进行定量分析。在第3 组实验中左边目标采用RNIM方法和fitting方法得到的重建结果与真实值之间的相对误差分别为2.69%和3.59%,右边目标重建结果与真实值之间的相对误差分别为5.99% 和15.27%。并分别采用两种方法对比分析重建目标的FWHM,采用RNIM 方法重建左边和右边目标的FWHM 分别为3.16 mm 和2.75 mm,而采用fitting方法得到结果是3.10 mm和2.65 mm。在第4组实验中左边目标采用RNIM 方法和fitting 方法得到的重建结果与真实值之间的相对误差分别为0.32%和0.48%,右边目标重建结果与真实值之间的相对误差分别为2.99%和15.57%。同样分别采用两种方法对比分析重建目标的FWHM,采用RNIM方法重建左边和右边目标的FWHM分别为4.20 mm和2.90 mm,而采用fitting方法得到结果是3.90 mm和2.85 mm。明显看出组织仿体为不同大小相同浓度和不同大小不同浓度时,相比于采用fitting方法定量重建仿体电导率,采用RNIM方法重建结果相对误差明显降低,精度提高。同时对比两组仿体目标重建的FWHM,采用RNIM 方法重建多目标仿体的特征属性与实际吻合度更高。
通过多目标仿体实验结果表明,在不同实验条件下,采用RNIM方法均能更加准确地定量重建组织仿体电导率,验证了RNIM方法的稳定性。并再次验证了采用RNIM方法对于早期肿瘤的定位和分期的精准检测具有重要意义。
3 结 论
本文所提出的基于RNIM的定量重建组织电导率的改进方法,通过数值模拟实验和组织仿体实验验证了该方法的有效性。在组织仿体实验中,该方法相比fitting 方法,目标在不同位置、不同大小、不同对比度情况下,定量重建仿体电导率的相对误差明显降低,并且重建大小与实际值可比拟。在仿体实验中,采用RNIM方法重建相同浓度的单目标在不同位置的电导率变化幅度更小,以及重建多目标电导率的相对比值与实际更接近,证明了改进方法的稳定性。通过不同浓度的单目标仿体实验,验证改进方法对浓度因素的良好泛化性。这对于肿瘤的定位和分期的早期筛查及精准诊疗,预防疾病恶化具有重要意义。下一步将通过离体/活体实验来进一步评估它的实用性。
需要指出,改进的方法虽然在重建结果的稳定性和精度上有所提高,但是改进的方法在组织仿体实验中未解决fitting方法中存在的电导率为负值的问题。因此,本文后续计划在该改进方法的基础之上提出一种新的方法来解决电导率为负值问题,为定量重建人体病变组织的电导率做好理论准备。