定量分析调控人类免疫缺陷病毒潜伏与激活的动力学机制*

熊瑞琪 苏洋 敖平*

（上海大学物理系，定量生命科学国际研究中心，上海 200444）

人类免疫缺陷病毒（human immunodeficiency virus，HIV）是获得性免疫缺陷综合征（acquired immune deficiency syndrome，AIDS）即艾滋病的病原体。艾滋病是一种广泛传播的流行病，截至2020 年，全球约有3 770 万HIV 感染者（https://aidsinfo.unaids.org）。目前治疗HIV 感染的主要方法为联合使用多种抗HIV 药物的高效抗逆转录病毒疗法（highly active antiretrovial therapy，HAART），该疗法能有效抑制艾滋病病毒的复制，将血液中的病毒载量降低至检测不到的水平，进而控制病情发展［1］。但处于潜伏态的病毒可以逃逸机体的免疫清除和抗病毒治疗，形成体内病毒潜伏存储库，在停止抗病毒治疗或治疗失败后，潜伏态病毒将会重新激活，导致病毒数量的迅速反弹，因此潜伏存储库是彻底治愈艾滋病的最大障碍。

为实现联合国艾滋病规划署到2030 年在全球消除艾滋病毒的目标，目前关于抗HIV 治疗的研究旨在清除病毒潜伏存储库，包括病毒转录编辑、基因编辑、激活并杀死（shock and kill）、阻断和锁定（block and lock）、干细胞移植和基因特异性转录激活等策略［2］。其中研究最多的是“激活并杀死”策略，即使用潜伏反转剂（latency reversing agents，LRAs）重新激活处于潜伏状态的病毒，使受感染的细胞被病毒本身或患者的免疫系统杀死，从而清除潜在病毒存储库［3］。“阻断和锁定”策略的目的则是创造一个永久性潜伏期，即通过病毒的转录和转录后基因沉默，产生一个永久的非生产性感染状态，从而抑制病毒的再次激活［4］。了解HIV 在潜伏状态与激活状态之间转换机制的理论基础对“激活并杀死”和 “阻断和锁定”这两种治疗策略的发展都有重要的指导意义。

在现代信息时代中，开关式结构是所有体系结构的重要组成部分。事实上，详细的分析已经表明，一个复杂网络的响应通常由各种开关［5］来处理，并且遗传网络被证明具有计算能力［6］。如今，生物开关的研究在细胞周期等过程中发挥了重要的作用，如λ噬菌体生命周期的基因开关［7］。同样地，对于目前全球大流行的新型冠状病毒感染（corona virus disease 2019，COVID-19）而言，潜伏态与激活态相互转换的分子机制也可以类似看作一个开关，不同的环境信号将导致其最终的发育途径。并且开关确实已经是生物过程的基本要素之一，也是生物学实验和理论研究的范例［8］。

HIV入侵宿主细胞后整合进宿主基因组形成原病毒（provirus），原病毒的复制受到转录起始和转录延伸两个过程的控制，其中转录起始过程主要受到宿主细胞因子的调控，而在转录延伸过程中病毒反式激活蛋白（trans-activator of transcription，Tat）构成的正反馈机制可以独立于宿主细胞状态调控原病毒在快速复制的激活态与转录沉默的潜伏态之间转换［9］，这样的转换就可以看作一个生物系统中的开关。目前已有理论［10］分析Tat 在促进HIV 转录延伸的过程中，其乙酰化速率和结合转录激活应答元件（trans-activation response，TAR）RNA 的速率等因素对病毒表达状态的影响，但当前理论［11-12］认为，HIV 调控网络的确定性动力学不足以解释所观察到的双稳态，需要使用随机性动力学来描述此机制。然而通过离散随机方程构建的模型使变量空间的探索范围受到了一定程度的限制，使得进一步的推广存在困难，并且目前的模型中都只包含了一部分影响因素，没有在同一个模型中对比所有不同影响因素的重要程度，存在一定的局限性。

本文使用连续的随机微分方程构建了调控HIV转录分子开关的动力学模型，将病毒的不同表达状态对应于系统的不同稳态，通过势函数和概率分布函数定量分析艾滋病潜伏期建立的分子机制。根据动力学结构分解下随机微分方程极值点与常微分方程稳定点的对应，仅需分析模型中方程的确定性部分就可以判断系统处于单稳态或双稳态的不同情况，从而分析病毒表达状态。在此基础上，参考现有实验数据计算出使稳态个数发生改变时的各影响因素的参数区间，并在理论上对比不同影响因素对于潜伏态与激活态之间转换的影响程度，为“激活并杀死”与“阻断和锁定”治疗策略提供了理论基础。本研究使用的连续方法相较于过去的离散方法在很大程度上缩减了变量存储空间的大小，可以更加方便地扩大模型中可调参数的变化范围、增加变量和参数的探索空间，有利于进一步发展彻底治愈艾滋病的可行的治疗靶点与药物。

1 材料与方法

1.1 HIV转录过程

原病毒的长末端重复序列（long terminal repeat，LTR）上包含多个细胞转录因子的结合位点，启动子和增强子序列可结合宿主细胞因子如Sp1、NF-κB、NFAT等从而促进转录起始，当宿主细胞处于活跃状态时，宿主细胞因子数量较高，更容易结合至LTR 促进转录起始。但在缺少Tat 的情况下，转录起始后，由于负延伸因子（NELF）的活性和阻止RNA 聚合酶II（RNA polymerase II，RNAp II）C 端结构域（CTD）磷酸化的DRB 敏感诱导因子（DSIF）造成的阻滞，RNApⅡ仅可在DNA 上移动一小段距离，生成少量且不完整的转录产物。病毒蛋白Tat 经过不同位点乙酰化以及与TAR RNA 结合的正反馈回路，可以将转录延伸所需的细胞因子如阳性转录延伸因子b（P-TEFb）等招募至RNAp II形成复合物，解除转录阻滞，促进转录延伸，生成大量且完整的转录产物（图1a）［9，13］。

Tat 促进转录延伸的正反馈机制如图1b 所示。首先，由赖氨酸乙酰转移酶（KAT）介导Tat K28位点的乙酰化，改变蛋白质构象，使其与由细胞周期蛋白T1（CycT1）和细胞周期依赖性激酶9（CDK9）组成的P-TEFb亲和力增强，形成复合物，并结合至TAR RNA；然后，KAT介导Tat K50位点的乙酰化，使复合物与TAR RNA 分离，作用于LTR 上，其中CDK9 过磷酸化RNAp II CTD，还能磷酸化DSIF 和NELF，使其对延伸过程的作用由负向正转变，从而可以解除RNAp II受到的阻滞作用，促进转录延伸［14］。HIV LTR 上发生的转录调控相关化学反应的整体流程图如图2所示。

1.2 常微分方程模型

控制和维持HIV功能的分子开关可简化地看作主要由LTR 和宿主细胞因子、Tat 组成，LTR 的不同结合状态如图1所示。未结合转录因子时的LTR状态记为LTRoff；宿主细胞因子结合至LTR 时促进转录起始，此状态记为LTRon；当宿主细胞因子和Tat 均结合至LTR 时促进转录起始和转录延伸，此状态记为LTRon-Tat。

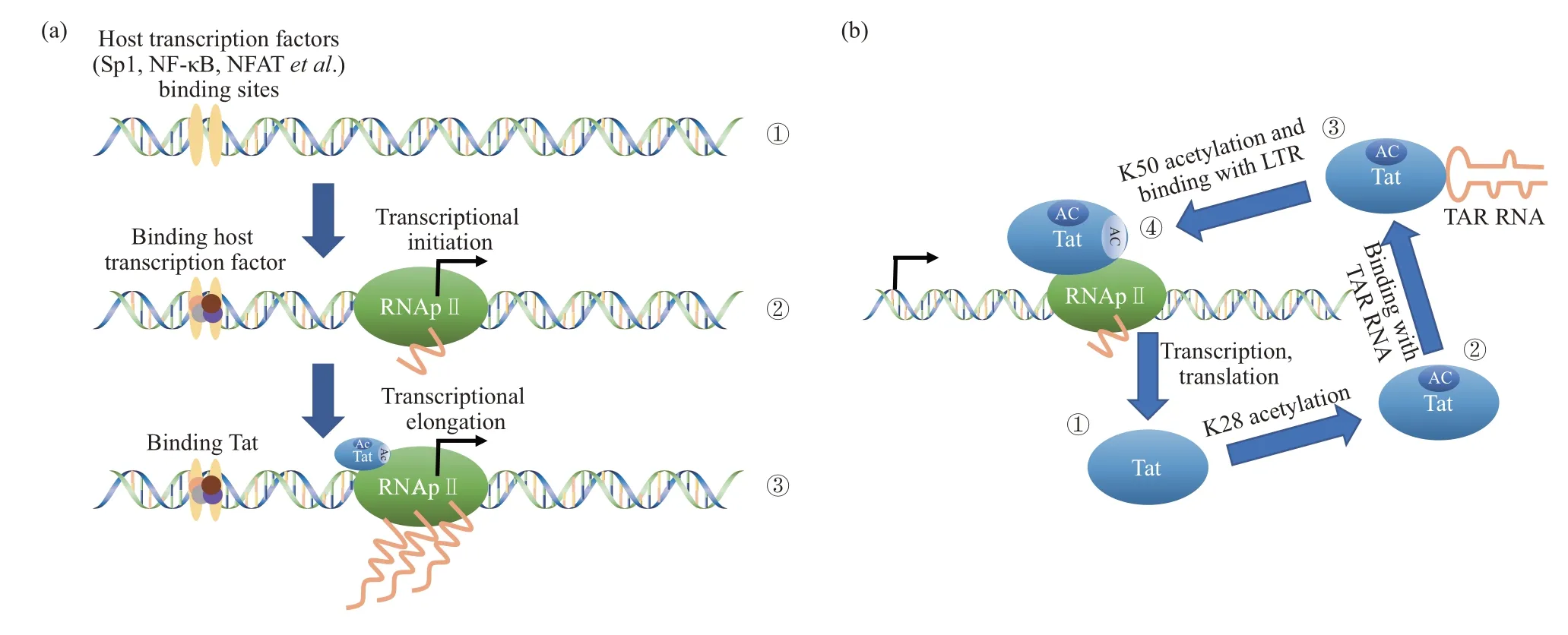
Fig.1 Transcriptional initiation and elongation on LTR (a) and the reaction process of Tat promoting transcriptional elongation (b)

Fig.2 The flow chart of transcriptional-regulated chemical reactions on LTR

病毒蛋白Tat 促进转录延伸的正反馈机制中包含图2 所示的多步修饰和结合反应，用变量x表示处于不同状态Tat 的总数量，在本模型中假设编码Tat的RNA数量与TAR RNA的数量相同，用变量y表示。经由转录、翻译后生成的无修饰Tat 记为Tat0，用a0表示其数量；K28 位点乙酰化的Tat 记为TatAc28，用a1表示其数量；处于与TAR RNA结合状态的Tat 记为TatAc28-TAR，用a2表示其数量；K50位点乙酰化的Tat记为TatAc50，用a3表示其数量；假设各状态Tat 均可招募反应所需因子，用R表示招募反应的平衡常数，则R×x为Tat所招募的因子如乙酰化辅酶（CoA）的数量。由K28位点乙酰化平衡常数k1、Tat与TAR RNA结合平衡常数k2、K50位点乙酰化平衡常数k3，可得平衡时各状态Tat 与作用于LTR 上促进转录延伸的TatAc50的关系为：

由Tat 总数量守恒，即x=a0+a1+a2+a3，可得TatAc50与Tat总数量的关系为：

想象一个充满LTR、宿主细胞因子和Tat 的化学平衡系综；C表示宿主细胞转录因子数量的影响，即结合于LTR 的宿主细胞转录因子（Sp1、NF-κB、NFAT等）的数量；l1、l2、l3分别表示3种不同结合状态即LTRoff、LTRon、LTRon-Tat的频数。在某一个时间点，真实的情况是，3种结合状态中有且仅有1种发生，在化学平衡的时候，各个结合状态的频数比值是恒定的，分别用P(1)、P(2)、P(3)表示LTR处于LTRoff、LTRon、LTRon-Tat结合状态的概率，此概率分布会随着蛋白质数量的改变而发生改变。

由宿主细胞因子结合于LTR 的平衡常数K1和宿主细胞因子结合时TatAc50结合于LTR的平衡常数K2可得频数l1、l2、l3之间的关系；把3种结合状态的频数加起来作为一个配分函数，即归一化因子，则处于LTRoff状态的概率、处于LTRon状态的概率、处于LTRon-Tat状态的概率。因此，LTR处于每种状态的概率分布为：

因此，Tat数量和RNA数量变化速率分别为：

其中：L表示翻译生成Tat 的速率常数，δt表示Tat降解的速率常数；N表示单个细胞中HIV DNA 的数量，在本文的计算中将其取为1［15］；T1、T2、T3分别表示LTR 处于LTRoff、LTRon、LTRon-Tat3 种不同状态时的转录速率常数；δr表示RNA 降解的速率常数。由于Tat 是由HIV 编码的蛋白质，因此可以其数量的高低作为病毒基因表达情况的表征，当Tat 数量较高时，表示病毒处于转录活跃即快速复制的激活态，反之则处于转录沉默的潜伏态。

1.3 动力学结构分解

随机性在生物学中是普遍存在的，本文模型里的随机性表现为细胞中大分子（蛋白质和RNA）数量的涨落。在动力学中，分子数量涨落的量级为N1/2，并且其修正项的量级为1/N1/2（当N特别大时可忽略），而在生物细胞中，大分子数目只有几十至几百个左右，因此其涨落是不可忽略的，即描述大分子数量随时间的变化的方程应包含随机性。对此，我们使用以下随机微分方程作描述系统动力学：

其中：qτ=(x，y)，τ表示转置；f τ(q)=(fx，fy)表示改变大分子数量的确定性非线性因素；ζ(q，t)表示系统噪声，假设其为均值为零的高斯白噪声，满足：

其中：正定对称矩阵D(q)为扩散矩阵，ε为噪声强度。

对于以上随机微分方程存在唯一的动力学结构分解［16］：

其中：正定对称矩阵S(q)表示摩擦力，即耗散，对应于生物学中的降解，会促进系统趋于能量较低的稳态吸引子；反对称矩阵A(q)表示横向力（洛伦兹力），对应生物学中的振荡，其不改变能量，对系统在不同稳态间的转换不起决定性作用，因此在本文所描述的开关现象中可将其忽略，但A(q)在非点状吸引子系统中会对动力学行为产生影响，例如细胞周期的调控［17］；单值标量函数U(q)表示势能函数；ξ表示随机力，与矩阵S(q)存在随机耗散关系：

将方程（5）代入方程（7），利用确定项的随机项的分别相等可以得到两个关系；随机项的相等引入了广义爱因斯坦关系：

确定项的相等得到：

为保证各部分的动力学性质的独立性，假设[S(q) +A(q)]非奇异，即det [S(q) +A(q)]≠0，因此方程（10）可变换为f(q)=-[S(q) +A(q)]-1∇U(q)=-[D(q) +Q(q)]∇U(q)，其中Q(q)是由[D(q) +Q(q)]=[S(q) +A(q)]-1决定的反对称矩阵，在确定项的不动点处f(q)=0，由det [D(q) +Q(q)]≠0可得势能函数U(q)的极值点与确定性动力学不动点的对应与扩散矩阵D(q)的具体形式无关，因此本文中为简化模型计算将其取为常数对稳态的分析不造成影响。

由势能函数的梯度的旋度为零的性质有：

方程（9）和（11）可由f(q)和D(q)求出S(q)和A(q)，从而进一步求得势能函数U(q)：

由势能函数U(q)可以确定分布函数：

其中ρ0为归一化常数，。使用这种随机积分方式求得的分布函数极值点与确定性部分常微分方程组的不动点一致，因此可以通过计算常微分方程组的稳定点分析系统的稳态情况。

2 计算结果

2.1 双稳态

本节计算中所代入的参数取值一部分通过查找相关文献获得，而另一部分未精确测量的参数取值，则根据文献中与其相关数据的大致数量级进行拟定，表1列出了模型中各参数的取值及相应参考文献。

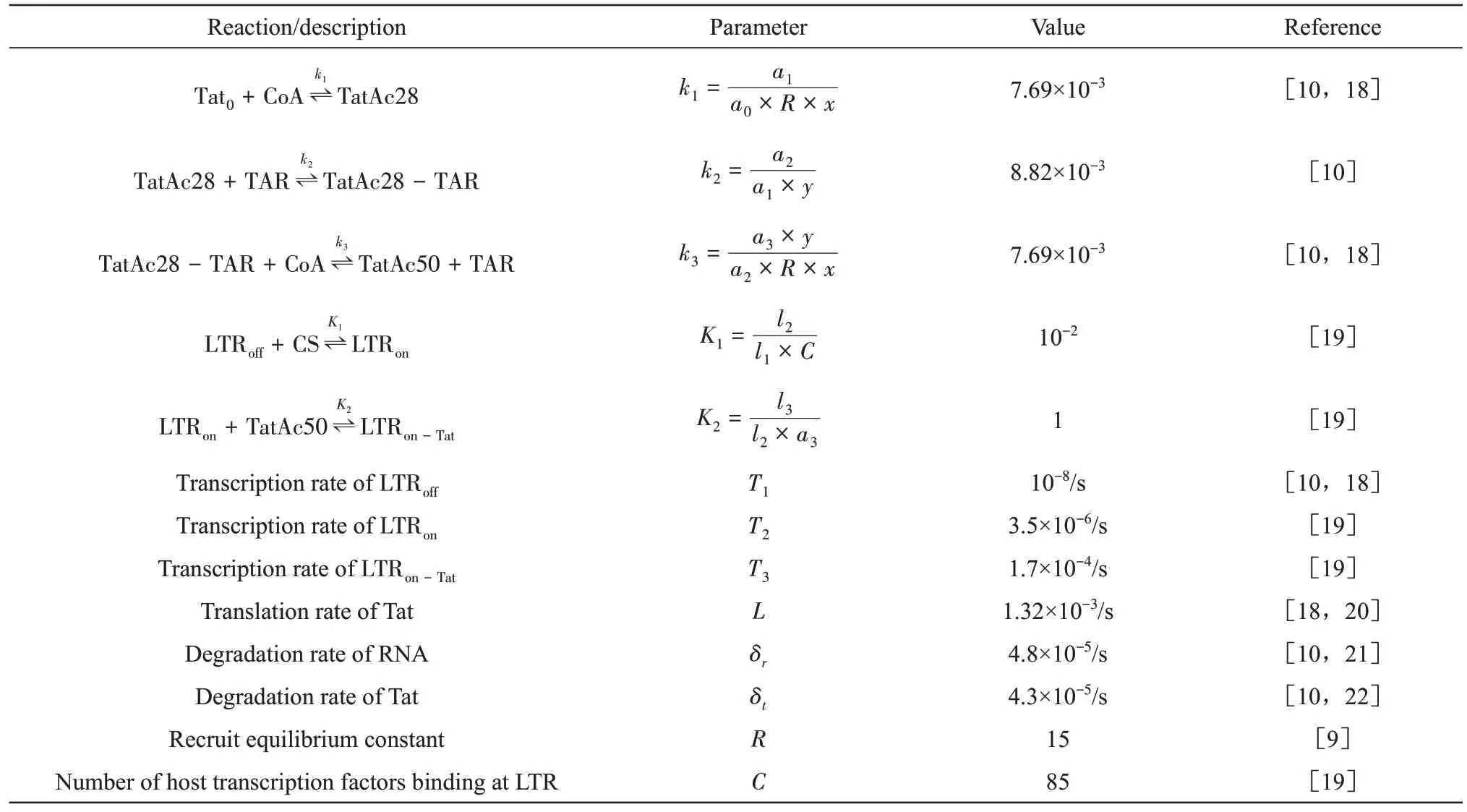
Table 1 Responses and parameters of positive feedback mechanism of HIV Tat

将表1中的参数取值代入方程（2）、（3）、（4）中，分别计算当Tat 和TAR RNA 初始值不同时其数量随时间的变化，得到结果如图3 所示。同时，通过牛顿法可以计算得出Tat 和TAR RNA 在潜伏态不动点、激活态不动点和鞍点的数值，分别约为1.0、78、35（Tat 数量）和0.033、2.5、1.1（RNA数量）。

2.2 稳态个数变化

为了研究参数变化对稳态个数的影响，在保持其余参数不变的情况下，调整其中一个参数值，并通过作图得出在不同Tat、RNA 初始值时Tat 蛋白数量和RNA 数量随时间的变化，同时用牛顿法计算出此时的稳态个数和相应数值（附件中第一部分），由此得到不同稳态个数所对应的参数区间。

根据参数的不同，系统可以表现出3种不同的稳态类型，以k2为例，其稳态分岔示意图见图4a（对应Tat 蛋白和TAR RNA 结合的平衡常数对稳态个数的影响）：a.只有潜伏态的单稳态，在k2较低（小于7.3×10-3）时，只存在1个Tat和RNA数量较小的潜伏态；b.只有激活态的单稳态，在k2较高（大于2.5×10-1）时，只存在1个Tat和RNA数量较大的激活态；c.双稳态，在上述两个k2值之间（7.3×10-3～2.5×10-1）存在两个稳态，由初始Tat 和RNA 数量决定最终稳态：当初始数量较高时，最终Tat和RNA数量稳定在高表达数量的激活态，反之，则稳定在低表达数量的潜伏态。

继续调节其余参数，得到不同稳态个数的参数区间（取两位有效数字）（表2）。当k1、k2、k3、K1、K2、C、R较低而δt、δr较高时，只存在潜伏态；当k2、k3、K2、R较高而δt、δr较低时，只存在激活态；另外，在本组参数下，单独调节k1、K1、C时（已调至1020，在本文模型中将其看作无穷大），未出现只存在单激活态的情况（附件中第一部分），其中以k1为例的稳态分岔示意图如4b 所示，以k1和k2为参数空间的相图如图4c所示。

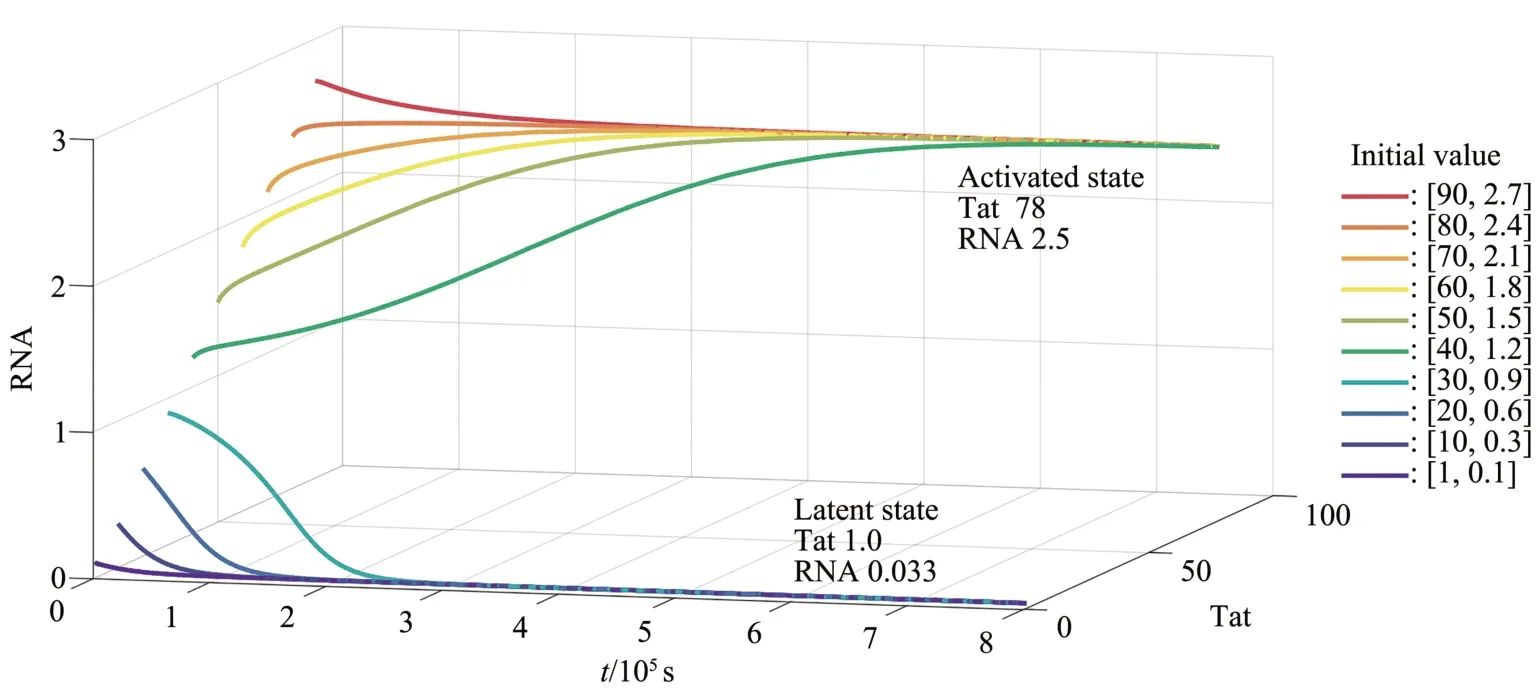
Fig.3 The number of Tat protein and RNA changed with time

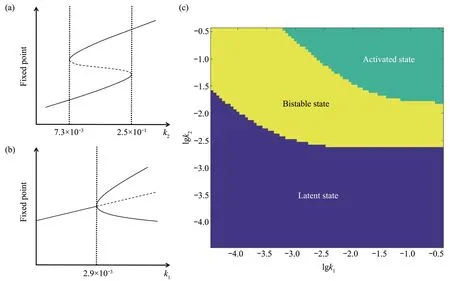
Fig.4 Bifurcation diagrams with parameters k1 and k2 as examples

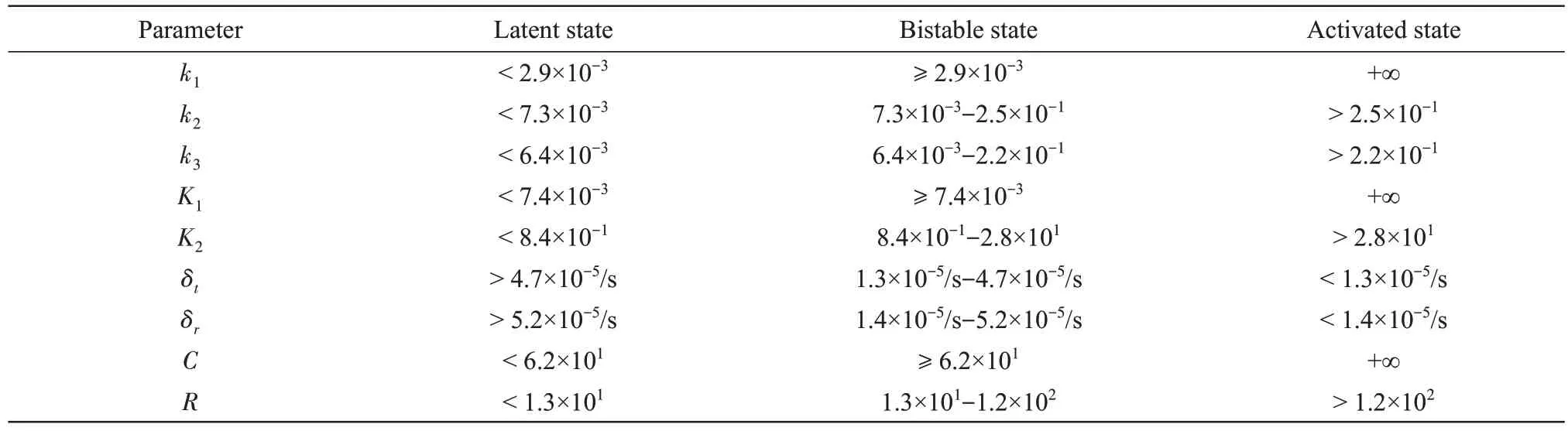
Table 2 Parameter ranges corresponding to different steady-state conditions

本小节通过调整不同的参数数值，分别得到了单潜伏态、双稳态和单激活态的情况，并且求出了不同稳态情况所对应的大致参数范围区间。

2.3 势能函数和概率分布

潜伏态和激活态之间的转换关系可以通过一个势能函数来表示，即1.3分解方法中的U(q)。取扩散矩阵D(q)为单位矩阵I、噪声强度ε=1，使用该方法计算原始参数情况下潜伏态和激活态相对于鞍点的势能差分别为ΔUb潜伏=0.003 5、ΔUb激活=0.003 1，即激活态比潜伏态更稳定。将鞍点处作为势能零点，相应的势能函数分布如图5a 所示，其中的两个低谷分别对应于两个稳定状态，即潜伏态和激活态；通过1.3所述随机积分方法计算得到的Tat和RNA数目概率分布函数图像如图5b所示，其中的两个峰值分别对应于潜伏态和激活态。由于运用此种随机动力学结构分解的方法求得的概率分布函数极值点与确定性部分常微分方程组的不动点是一致的，说明加入噪声项不影响不动点的数值。图6为取ε=5时的势能函数与Tat和RNA数目的概率分布，对比图5和图6中稳态所对应的数值可以看出（由于只关注鞍点及稳定点附近的性质，图5中未展现出U＞ 5.0×10-3，P＜ 1.002×10-4时其余地方的变化，图6中则未展现出U＞ 1.0×10-3，P＜ 1.002×10-4时其余地方的变化），噪声强度的改变不影响不动点的数值。因此，仅需分析常微分方程确定性部分就可以求得稳态所对应Tat 和RNA 的数值。

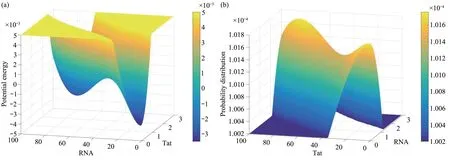
Fig.5 Potential energy function diagram when ε=1 (a) and probability distribution diagram when ε=1 (b)

Fig.6 Potential energy function diagram when ε=5 (a) and probability distribution diagram when ε=5 (b),which are consistent with Figure 5

另外，当参数改变时，相应的势能函数与Tat和RNA 数目的概率分布会有所变化，可以从势能数值的高低和概率分布的大小来判断在不同参数下各稳态的稳定性，即当势能相对较低、分布概率高时，相应的稳态较稳定（附件中第二部分）。

3 讨 论

3.1 潜伏期建立机制

3.1.1 稳态个数

系统的稳态个数发生变化表明其动力学结构出现分岔。本模型有仅存在潜伏态的单稳态、同时存在潜伏态和激活态的双稳态、仅存在激活态的单稳态3种不同的稳态情况：当系统仅存在潜伏态所对应的单稳态时，HIV一定会进入潜伏期；当系统同时存在潜伏态和激活态的双稳态时，HIV有一定几率进入潜伏期；当系统仅存在激活态所对应的单稳态时，HIV一定不会进入潜伏期。由方程（10）可看出系统的稳态情况与随机性因素如扩散矩阵无关，仅与确定性因素如参数取值有关，各不同参数情况与稳态个数的对应如2.2中计算结果所示。

3.1.2 稳定性分析

当系统同时存在潜伏态和激活态的双稳态时，不同稳态间的转换即为HIV在潜伏态与激活态之间的表型转换。根据2.3中的计算结果，不同参数情况下系统各稳态的势能不同，会导致处于各稳态的概率以及稳态间转换的概率不同。当潜伏态比激活态更稳定时，HIV进入潜伏期的概率较大，并且更容易从激活态转换至潜伏态［23］；当激活态比潜伏态更稳定时，HIV处于活跃复制的激活状态的概率较大，并且更容易从潜伏态转换至激活态。系统各稳态的稳定性同时受到确定性因素和随机性因素的影响，但随机性的噪声强度仅影响势能的数值大小，并不改变极值点所对应的大分子数值（图5、6），即HIV发生表型转换的概率会受到随机性因素的影响，但处于稳定状态时的大分子数量与随机性因素无关。

3.2 影响因素

3.2.1 宿主细胞状态

根据1.2的模型，方程中的参数C和K1分别表示宿主细胞因子的数量以及宿主细胞因子对LTR的作用程度，表征了宿主细胞状态在转录过程中的影响。由2.2中的计算结果，可以得出的结论，当宿主细胞因子数量较少、对LTR 作用程度较弱，即宿主细胞处于静息状态时，仅会存在潜伏态的单稳态；当宿主细胞因子数量增加、对LTR 作用程度增强，即宿主细胞状态转变为活跃状态时，系统会出现潜伏态和激活态并存的双稳态。在双稳态区间内，宿主细胞状态的改变不会影响病毒表达，即病毒的状态可以独立于细胞状态自主调控，与实验现象［19］一致；而当宿主细胞状态的变化超出了双稳态区间时，就会对病毒的表达情况产生影响。但在本文的参数条件下，C和K1的增加均不会导致仅存在激活态的单稳态出现，即无法使潜伏态的稳态消失，说明该状况下宿主细胞的激活无法彻底清除病毒存储库。

3.2.2 Tat正反馈机制

在Tat正反馈的反应过程中，Tat的乙酰化难易程度、Tat 与TAR RNA 的亲和力、Tat 降解速率与招募反应效果均会影响正反馈的强弱。

在1.2的模型中，当k2、k3较小，即Tat-TAR结合速率较低而分离速率较高、TatK50 位点的去乙酰化速率较高而乙酰化速率较低时，Tat 正反馈强度较小，系统仅存在潜伏态的单稳态，随着k2、k3的增大，系统会出现潜伏态和激活态并存的双稳态，继续增大则会仅剩下激活态的单稳态；招募反应平衡常数R的增大也会导致系统的动力学结构出现同样的分岔行为。但由2.2中的计算结果可以看出，Tat 在K28 位点的乙酰化对系统稳态个数的影响程度较弱，平衡常数k1的增加不会使潜伏态的稳态消失。

而当Tat的降解速率δt较小，即Tat半衰期较长时，Tat 正反馈强度较大，系统仅存在激活态的单稳态，随着δt的增大，系统会出现潜伏态和激活态并存的双稳态，继续增大则会仅剩下潜伏态的单稳态。因此，当Tat 半衰期的变化较剧烈，越过了分岔临界值时，HIV 表现出的稳态类型就会发生变化，即改变Tat 正反馈的强度可以在不激活细胞状态的情况下使病毒表达在潜伏态与激活态之间转换，与实验现象［19］一致。

3.2.3 噪声

将2.1中由常微分方程计算得到的稳定点数值与2.3中分解随机微分方程计算出的势能和概率分布的局部极值点对比，可以验证稳态所对应的大分子数值仅由确定性因素决定，即噪声不影响系统动力学结构的分岔，因此当系统仅存在单稳态时无论噪声强度如何HIV都不会发生表型转换；但噪声会影响势能和概率分布的数值大小，即处于双稳态区间的系统发生表型转换的难易程度同时受到确定性因素和随机性因素的影响，而当确定性因素不变时，能否在足够短的时间内发生表型转换受到噪声的驱动，由于生物系统中噪声的普遍存在，实验中可以观察到HIV 在潜伏态与激活态之间随机转换［18］。需要强调的是，噪声只是导致表型转换而并非产生双稳态的原因，双稳态的存在由确定性动力学的分岔结构决定。

4 结 论

HIV 潜伏库的存在极大阻碍了艾滋病的治愈，本研究通过建立调控HIV 转录过程分子开关的动力学模型定量分析了潜伏期的建立机制，并探究了不同因素对系统稳态情况的影响，对激活病毒潜伏库的临床治疗具有指导意义。本文模型中所使用的连续随机微分方程相较于以往离散的方法在很大程度上增加了变量和参数的探索空间，有利于进一步扩大模型范围，并在一定程度上促进了寻找彻底治愈艾滋病的有效的治疗靶点与药物的进程。

利用本文中的模型，可以计算出在不同参数下，系统动力学结构所存在的稳态情况，即处于单稳态或者双稳态，在此基础上，可得到各稳态所对应的势能，并通过不同参数对稳态数量以及势能大小的影响评估不同药物靶点的治疗程度，例如当调节参数取值越过分岔临界值，使系统由双稳态变为仅存在激活态的单稳态时，该参数所对应的药物治疗即可达到彻底激活病毒库的效果。对比2.2计算结果中各参数在双稳态区间取值范围，可以初步得出，宿主细胞状态和Tat 在K28 位点乙酰化的难易程度对稳态个数变化的影响程度较弱。因此，在本文所拟定的参数调节下，应更着重于发展调控Tat-TAR 亲和力、TatK50 位点乙酰化、Tat 的招募反应效果以及Tat半衰期的药物靶点，与目前已有的生物学实验结果一致，验证了本工作的理论基础。当临床上可以测得不同病人的体内参数具体数值时，则可通过本文的方法计算分析稳态及势能的情况，从而在理论上得出更加有效的药物靶点，指导制定针对相应病人的个性化治疗方案。

总的来说，本文的研究结果表明，在建立调控HIV 转录的分子开关的随机动力学模型的基础上，通过定量分析方程中确定性部分的动力学结构，可以得到潜伏期建立的分子机制及各药物靶点的治疗效果，有利于进一步了解艾滋病在生物体内的发生发展机制，为临床治疗提供理论指导。

附件见本文网络版（http://www.pibb.ac.cn或http://www.cnki.net）：

PIBB_20220053_Doc_S1.pdf