基于SSA-LSTM模型的黄鳝池溶氧预测研究

林彬彬，袁 泉，田志新，潘显斌，周文宗，徐 震

(1 上海工程技术大学机械与汽车工程学院，上海 201620；2 上海市农业科学院，上海 201403)

黄鳝，又名鳝鱼，可食用，也可入药，在中国和东南亚广泛分布[1]。当前市场上大部分的黄鳝来源于人工养殖。溶氧是影响黄鳝养殖的重要因素。水体中较高的溶氧含量会促进有机物的分解，降低水体中的有害物质，为黄鳝营造一个优良的生长环境[2]。而较低的溶氧含量则会导致黄鳝出现浮头现象[3]。目前溶氧数据主要是依赖于传感器的实时获取[4]。但是传感器数据仅能获取当前状态，无法对异常数值进行预警，从而有可能导致养殖风险的发生。因此需要对水质问题做出预警并提前处理，溶氧参数的预测便十分重要。

溶氧作为水质参数的一种，具有非线性特征[5]，传统的预测方法主要是基于实践经验和数值模拟，但是这两种方法需要具有丰富的实践经验或者建立在大量数据的基础上，两者皆无法建立普遍适用的模型。

使用机器学习建模为水质预测提供了一种新的方案。这些模型有许多好处：(1)无需具有丰富的实践经验；(2)减少了时间和成本(如材料和劳动力成本)；(3)简化了复杂的预测系统。目前，已有多种机器学习算法成功用于水质参数预测。Deng等[6]利用支持向量机(SVM)成功预测了香港吐露港海藻的变化趋势。Li等[7]利用离散隐马尔可夫模型(DHMM)和K-means聚类方法构建了水质参数预测模型，用于预测环渤海6个海洋牧场的溶氧饱和度和浊度。Peng等[8]利用差分进化算法对模糊神经网络(FNN)参数进行优化，建立了水产养殖水质溶氧的非线性预测模型，对对虾养殖池水质数据进行了预测。对于具有时间序列特征的数据，循环神经网络(RNN)[9-11]以及其变型门控循环单元(GRU)[12-14]、长短期记忆神经网络(LSTM)[15-17]是最常用的方法。

几乎所有神经网络模型都需要人工去设置超参数，这具有较高的随机性，会降低模型的预测效果[18]。为解决这个问题，一种可行的方法是利用元启发式优化算法[19]对神经网络模型中的超参数进行优化。元启发式优化算法主要分为三种，一种为仿生物种群的优化算法，如粒子群算法(PSO)[20-21]、人工蜂群算法[22]、灰狼算法[23]，第二种为仿物理化学过程的优化算法，如模拟退火算法[24]，第三种为仿遗传进化规律的优化算法，主要包括遗传算法[25]。Xue等[26]基于麻雀的觅食与反捕食行为提出麻雀搜索算法(SSA)，该算法搜索速度快、收敛精度高、鲁棒性强，具有较强的全局寻优的能力，可以有效地防止陷入局部最优。

本研究利用麻雀搜索算法(SSA)以提高LSTM模型准确度为优化目标，以LSTM模型中超参数为优化对象，对LSTM进行优化，搭建SSA-LSTM神经网络模型；将SSA-LSTM模型用于水质溶氧参数的预测，并与LSTM、GRU、PSO-LSTM算法作对比。

1 材料与方法

1.1 数据来源

使用水质在线监测仪(Manta+40，美国Eureka)监测上海市农业科学院庄行综合试验站黄鳝循环水养殖池(20 m2)水质，现场如图1所示。

图1 黄鳝循环水养殖池

黄鳝养殖池位于玻璃大棚内部，养殖水位30 cm，水泥池配有循环水过滤系统，无其他增氧设施。本研究利用了2020年3月31日13:00至2020年5月31日12:00的溶氧监测数据。

1.2 研究方法

1.2.1 长短期记忆神经网络

RNN是机器学习方法之一，主要用于处理时间序列数据。RNN的网络结构如图2所示，有一个自连接的隐藏层，它的当前状态可以依靠前一时刻输出进行更新，因此可以解决时间序列的长期依赖问题。

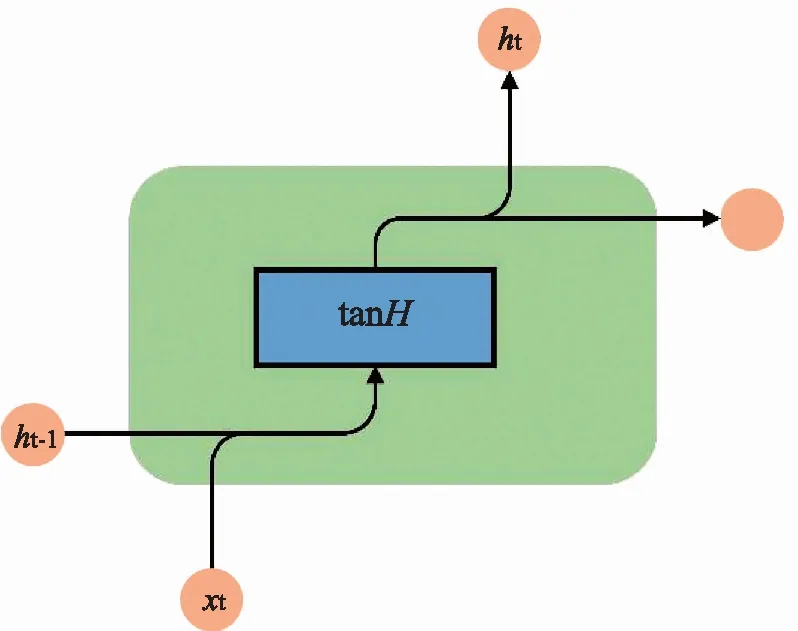
图2 循环神经网络网络架构图

但是对于较长的时间序列，在实际RNN的使用过程中，会出现梯度消失和梯度爆炸的现象。为了解决以上问题，提出了LSTM。LSTM是基于RNN的一种改进，它保留了RNN自连接的隐藏层，而且隐藏层中的节点更为复杂，可以实现较长时间序列的信息保留[27]。

LSTM由遗忘门、输入门和输出门三部分组成。通过巧妙的结构设计(图3)，很好地解决了RNN对于较长的时间序列状态无法传递的问题。

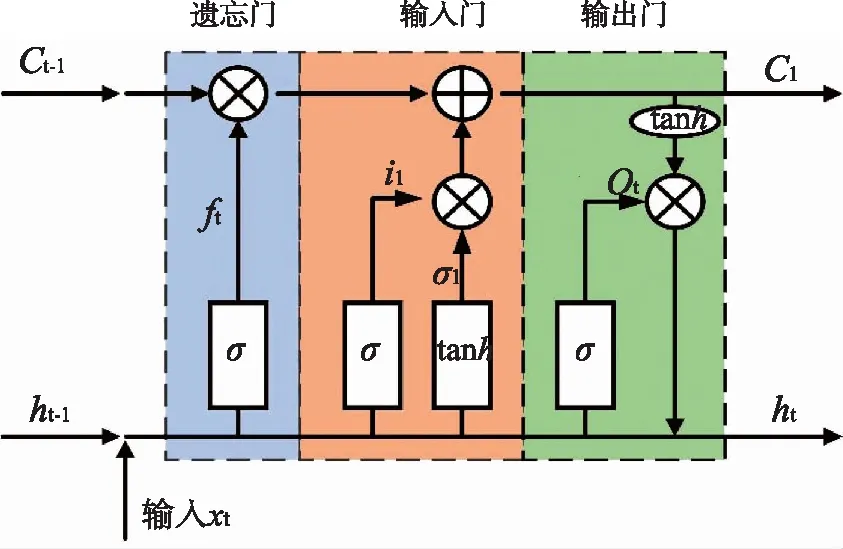
图3 长短期记忆神经网络架构图

遗忘门：遗忘门的功能是判断应舍弃哪些信息。

ft=σ(Wf·[ht-1,xt]+bf)

(1)

输入门：输入门的功能是决定输入哪些信息。

it=σ(Wi·[ht-1,xt]+bi)

(2)

(3)

输出门：输出门确定当前状态的输出。

Ot=σ(WO·[ht-1,xt]+bO)

(4)

ht=σt[tanh(Ct)]

(5)

式中：σ为sigmoid函数，tanh为tanh函数，Wf、Wi、WC、WO均为权重矩阵，bf、bi、bC、bO均为偏置矩阵，ht是当前状态的输出结果，xt是当前状态的输入，Ct是当前的隐藏状态。

1.2.2 麻雀搜索算法

麻雀搜索算法模拟麻雀觅食过程中行为，将种群的麻雀分为三类，一类是生产者，负责寻找食物，引导种群前往食物丰富的区域；另一类是跟随者，在觅食的过程中它们会时刻观察着生产者，一旦发现生产者找到了更好的食物，会立刻放弃自己现在的食物，转向生产者。此外种群中还有一定比例的警戒者，没有危险时就在种群中随意走动，一旦发现了危险就立刻向安全区域移动。在迭代的过程中，他们按照会一定的规则进行更新位置信息。生产者:

(6)

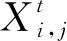
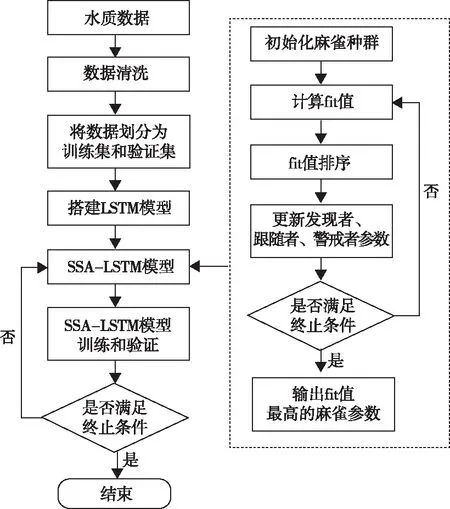
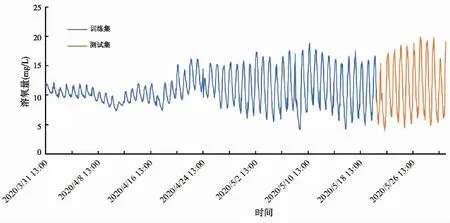
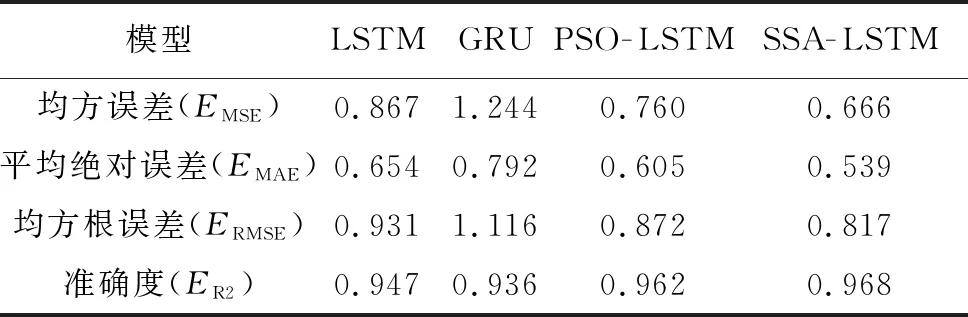
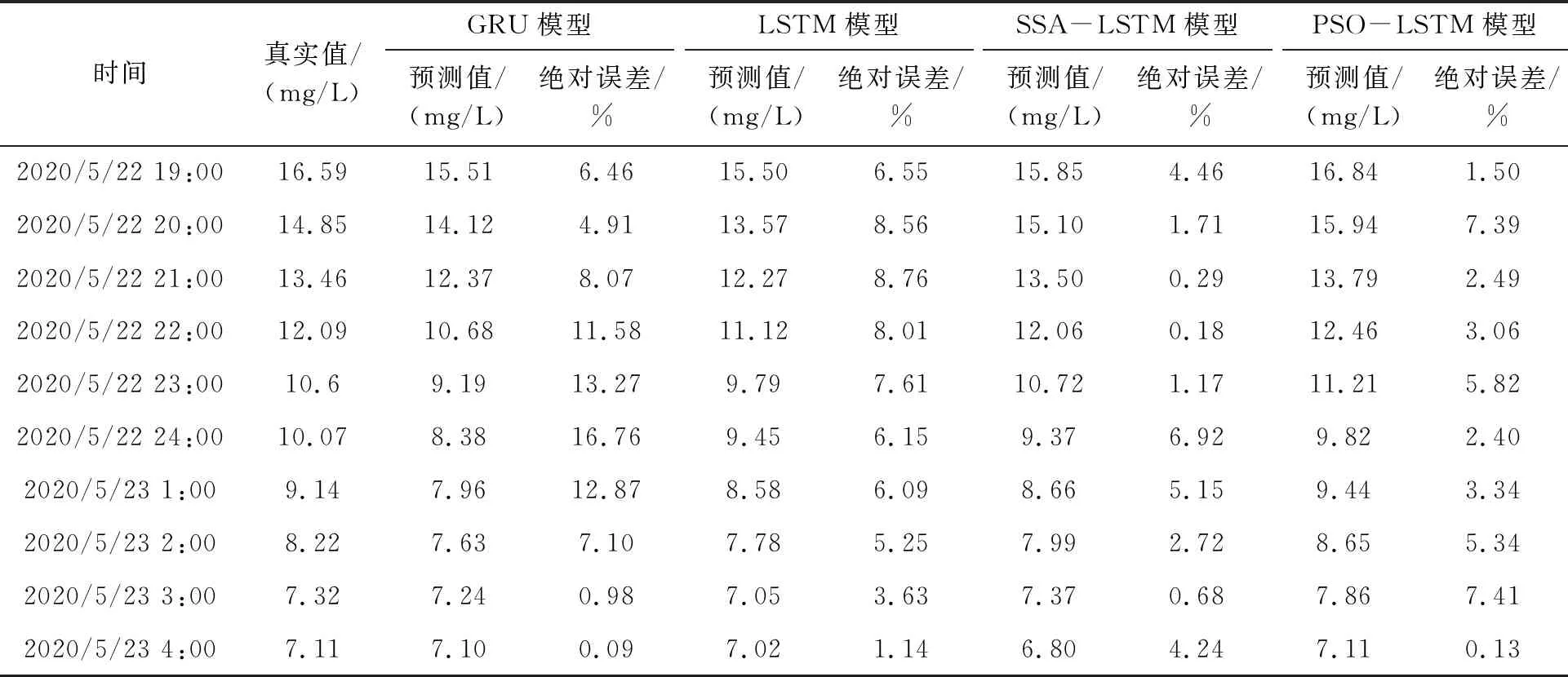
当AL

跟随者：

(7)

式中：n为当前麻雀种群的总数，XP是当前种群占据最好位置麻雀的位置。Xworst是当前种群占据最差位置麻雀的位置。A是一个满足A+=AT(AAT)-1的1×d矩阵，A中的元素随机取1或者-1。

如果i大于n/2，则表示当前的麻雀位置不好，可能会挨饿，因此需要飞往更远的地方去觅食。如果i小于或等于n/2，说明当前麻雀位置尚可，只需向位置最好的麻雀靠近即可。

警戒者：

(8)

当fi>fg时，代表当前麻雀处于种群的边缘，极易受到攻击。当fi=fi时，表示处于种群中心的麻雀意识到危险，开始向其他麻雀移动，减少被捕食的风险。

2 建立SSA-LSTM水质参数预测模型

预测模型流程如图4所示。

图4 SSA-LSTM算法模型框架

在LSTM神经网络中，隐藏层神经元的个数是影响模型性能关键性的超参数。除此以外，dropout层对模型的拟合程度也有着重要影响，dropout层的超参数值过小，模型会出现过拟合问题。针对水质数据的特点，利用SSA以LSTM中隐藏层神经元个数和dropout层的超参数为优化对象，以提升性能指标准确度(ER2)为优化目标，搭建SSA-LSTM预测模型。

具体步骤如下：

1)数据处理：数据处理是建模的基础。在数据采集的过程中，会受到各种因素的影响，数据会出现缺失、数据异常(如违背常识的错误、数据的离群值、数据格式不一致)，将会对建模的结果造成影响，因此需要对原始数据进行规范化的处理。首先对缺失和异常的数据利用拉格朗日插值法插值处理。接着将数据进行归一化处理，统一映射到[0,1]中。归一化处理可以加快模型的收敛速度，提高预测精度。最后将数据划分为训练集与验证集。

(9)

式中：x、y分别为数据对应的横、纵坐标。

(10)

式中：xmax、xmin分别为数据集中最大值、最小值。

2)利用SSA对LSTM进行优化。

a)麻雀搜索算法参数初始化。确定麻雀总数、生产者数量、跟随者数量、警戒者数量、迭代总数、初始麻雀的位置参数、安全阈值(ST)。

b)将性能指标准确度(ER2)作为适应度(fit)值，ER2取值介于[0,1]之间，越接近于1代表模型的预测精度越高。根据麻雀的适应度值来计算种群最优和最差的位置。

c)根据麻雀搜索算法公式进行迭代，取fit值前20%为生产者，20%至90%为跟随者，最后10%为警戒者。

d)判断是否满足终止条件，如果满足输出当前麻雀的位置参数和fit值。否则继续执行b和c。

3)利用SSA优化后的参数，建立LSTM模型和训练神经网络。

4)训练好的LSTM模型用来预测测试集和评估模型误差。本研究选取均方根误差(ERMSE)、均方误差(EMSE)、平均绝对误差(EMAE)和准确度(ER2)作为评价指标来评价模型的预测效果。

(11)

(12)

(13)

(14)

3 试验与结果分析

3.1 数据处理

清洗后的数据分布如图5所示。

图5 黄鳝池溶氧变化曲线

由于在数据采集的过程中，容易受到各种因素的干扰，因此首先需要进行数据清洗工作。主要是对缺失值的插补和对异常值的剔除。然后用2020年5月21日之前的数据用作训练集，2020年5月21日至2020年5月31日的数据用作测试集。

3.2 搭建模型

建立SSA-LSTM预测模型和3个对比模型(LSTM、GRU、PSO-LSTM)，模型结构参数如表1所示。

表1 模型结构参数表

3.3 结果分析

将处理后的数据导入SSA-LSTM模型和对照模型中进行预测，其中SSA-LSTM模型预测准确率为96.77%，相对于LSTM、GRU、PSO-LSTM模型性能对比如图6所示。

图6 不同模型预测结果与真实值对照图

由图6可知，每个模型对于溶氧的变化趋势预测拟合基本一致，但是SSA-LSTM拟合度最高。通过4种评价指标(EMAE，ERMSE，EMSE，ER2)可以更加直观地显示4种模型的性能表现，如表2所示，其中SSA-LSTM模型相对于LSTM和GRU模型，ER2分别提升了2.09%、3.34%，EMSE分别下降了23.1%、46.4%，EMAE分别下降了17.5%、32.0%，ERMSE分别下降了12.3%、26.8%。

表2 模型评价指标

基于上述指标表明，利用麻雀搜索算法优化后的LSTM模型的预测精度和性能优于未被优化的LSTM模型。相对于PSO-LSTM模型ER2提升了0.55%，EMSE下降了12.3%，EMAE下降了10.9%，ERMSE下降了10.9%。基于上述指标表明，利用麻雀搜索算法优化后的LSTM模型的预测精度和性能优于利用粒子群算法优化后的LSTM模型。

孙龙清等[28]利用天牛须搜索算法(IBAS)优化LSTM，提出了IBAS-LSTM溶氧预测模型，模型预测结果EMSE为0.683 6，ERMSE为0.826 8，EMAE为0.542 8，通过结果可以看出，其模型性能与本研究提出模型性能基本一致。胡衍坤等[29]利用具有周期性的差分自回归移动平均模型(SARIMA)与LSTM相结合，提出SARIMA-LSTM模型对河流水质指标中的化学需氧量进行预测，模型预测结果EMSE和ERMSE分别为3.17、1.37，模型性能不如本研究提出SSA-LSTM模型性能优越。陈英义等[30]利用卷积神经网络(CNN)对RNN进行优化，提出CNN-RNN模型对水产养殖中溶氧参数进行预测，模型结果EMAE、ERMSE、ER2分别为0.138、0.229、0.954，其中ER2没有本研究模型的效果好，但是EMAE、ERMSE两项评价指标要优于本研究模型，分析原因为在水质参数采集的过程中，容易受到各种环境因素的干扰，这些干扰因素在水质参数数据中会以噪声的形式存在，陈英义等在对数据处理的过程中，采用了小波降噪的处理方式，降低了环境噪声的干扰，因此其EMAE、ERMSE会优于本研究模型。但是这样会增大模型运算时占用的资源，考虑到在实际生产活动中模型需要符合轻量化布置的要求，便没有将小波降噪加入到模型中。通过上述对比可以看出，本研究提出的SSA-LSTM模型具有较高的预测精度和预测质量，值得推广和应用。

为了测试模型在连续性预测过程中的表现，随机选取连续10个点的4个模型预测值和真实值，其中GRU、LSTM、PSO-LSTM模型的平均绝对误差分别为8.21%、6.18%、3.89%，而SSA-LSTM模型的平均绝对误差为2.75%，低于对照模型。SSA-LSTM模型的最大绝对误差为6.92%，而GRU、LSTM、PSO-LSTM模型的最大绝对误差分别为15.51%、8.76%、7.39%，SSA-LSTM相对于对照模型分别下降66.45%、55.41%、29.22%。证明SSA-LSTM模型在连续性预测工程中具有优越的性能。各模型实际值与预测值绝对误差对比如表3所示。黄鳝池溶氧模型的泰勒如图7所示。

表3 各模型实际值与预测值绝对误差对比

图7 黄鳝池溶氧模型的泰勒图

图7是上海市农业科学院循环水黄鳝养殖池的溶氧预测模型性能的泰勒图[31]。泰勒图是基于预测值与真实值的相关系数、均方根误差和标准差绘制的可以更加直观描述模型性能的工具。图中的散点代表着本试验的模型，径向参数代表相关系数，横轴和纵轴代表标准差。GRU模型的相关系数为0.975，标准差为1.02。LSTM模型的相关系数为0.978，标准差为1.11。PSO-LSTM的相关系数为0.983，标准差为1.01。SSA-LSTM模型的相关系数为0.984，标准差为0.998。其中SSA-LSTM模型相较于其他对照模型具有最强的相关性和最低的标准差，因此SSA-LSTM模型相较于对照模型对于黄鳝池溶氧的预测性能最好。

4 结论

提出了SSA-LSTM模型，利用麻雀搜索算法对LSTM隐藏层中神经元的个数、dropout层的丢弃率超参数进行迭代寻优，克服了人工选取超参数的随机性和不确定性对模型的影响。利用SSA-LSTM模型对上海市农业科学院庄行综合试验站黄鳝循环水养殖池的溶氧参数进行预测，准确度、均方根误差、均方误差、平均绝对误差分别为96.77%、0.67、0.53、0.81，相较于对照模型准确度有明显提升，均方根误差、均方误差、平均绝对误差有明显下降，结果表明SSA-LSTM模型的预测精度和鲁棒性都优于其他几种模型。本研究只是使用单个变量的数据集对溶氧进行预测，在现实中，水质多个参数间存在着复杂的耦合关系。分析参数间的耦合关系，并利用这种的耦合关系实现对关键性参数的预测，在未来将是一个很好的研究方向。

□