基于VOF方法的团山子水利枢纽溢流坝数值模拟

姚 迟，姜 湖

(1.水利部河湖保护中心，北京 100038;2.广东水科院勘测设计院，广州 510635)

1 概述

在20世纪中期，人们便建立了数学模型的基本理论，并在计算机出现以后得到了广泛应用。1952—1954年期间，Twesch和Isaacson对密西西比河和俄亥俄河的部分河段建立了数学模型，模拟了实际洪水的过程。在计算机技术迅速发展的20世纪60年代，通过计算技术与水力学的结合，解决疑难问题的能力进一步提高。随着技术的进步和发展，水流数值模拟的研究日趋成熟，在水利工程领域中得到广泛的应用[1]。20世纪70年代，求解泄水建筑物水流的方法多采用以势流理论与边界层理论为基础的计算水力学，由于在局部区域产生分离流会形成回流旋涡流场，一部分能量会在内部损失，而这部分能量并不能忽略，因此势流理论并不适用，需采用紊流数学模型[2-3]。

20世纪80年代，水利工程一般采用简单的如普朗特的混合长度理论等的紊流模型进行数值模拟，但无法解决水工水力学中遇到的各种复杂流场问题。由于计算技术和数值方法的发展，有关数值解研究和紊流模型取得较大进展。紊流模型的逐步应用，使高雷诺数水流数值解的范围也逐步提高。泄水建筑物水力特性的数值模拟，与试验数据对比后，逐步验证和率定了紊流数值模型。杨永全等[4]曾对因受固体边界约束的水垫塘内的淹没射流做过分析，发现其流动特性与淹没自由射流具有各向异性的特点，并用紊流代数应力模型比较分析计算结果与试验实测资料之间的差异。倪浩清等[5]对室内浅水水池中的流动进行了紊流全场模型模拟，验证了全场模型所预报的输移扩散规律的可靠性。陶建华等[6]用有限差分法求解，采用k～ε紊流模型求解弱可压流动模型的方法，研究因溃坝而引起的复杂流场，发现符合给出自由面的变化规律及流场的非定态过程。陈黎等[7]对表孔泄洪进行了二维数值模拟并与模型试验对比，表明水气二相流VOF法数学模型是可行的。戴春胜[8]验证了VOF方法结合较精细的k～ε数值模型对河道地形复杂情况下河道水流泥沙运动模拟的可行性。本文在前人研究的基础上，采用了FLUENT软件对溢流坝水力特性进行数值模拟，为工程设计优化提供依据。

2 工程概况

团山子水利枢纽工程位于蛟河市前进乡团山子村二社境内，坝址座落在蛟河支流义气河下游，是吉林省重点水利工程项目。该工程主要由土石坝、电站厂房、溢流坝、砼挡水坝、取水阀室及城市供水管线组成。其中溢流坝位于桩号坝0+792 m～坝0+832 m，长度为40 m，由WES型实用堰、消力池段、护坦段、海漫段及尾水渠组成，结构形式为WES型实用堰，溢流坝分3孔，前缘净宽为30.0 m，堰顶高程为330.00 m，单孔净宽为10.0 m，溢流坝堰面曲线方程为y=0.112×x1.85，上游面坡度1∶0.3，反弧段反弧半径为10.0 m，直线段坡度为1∶0.75(如图1所示)。

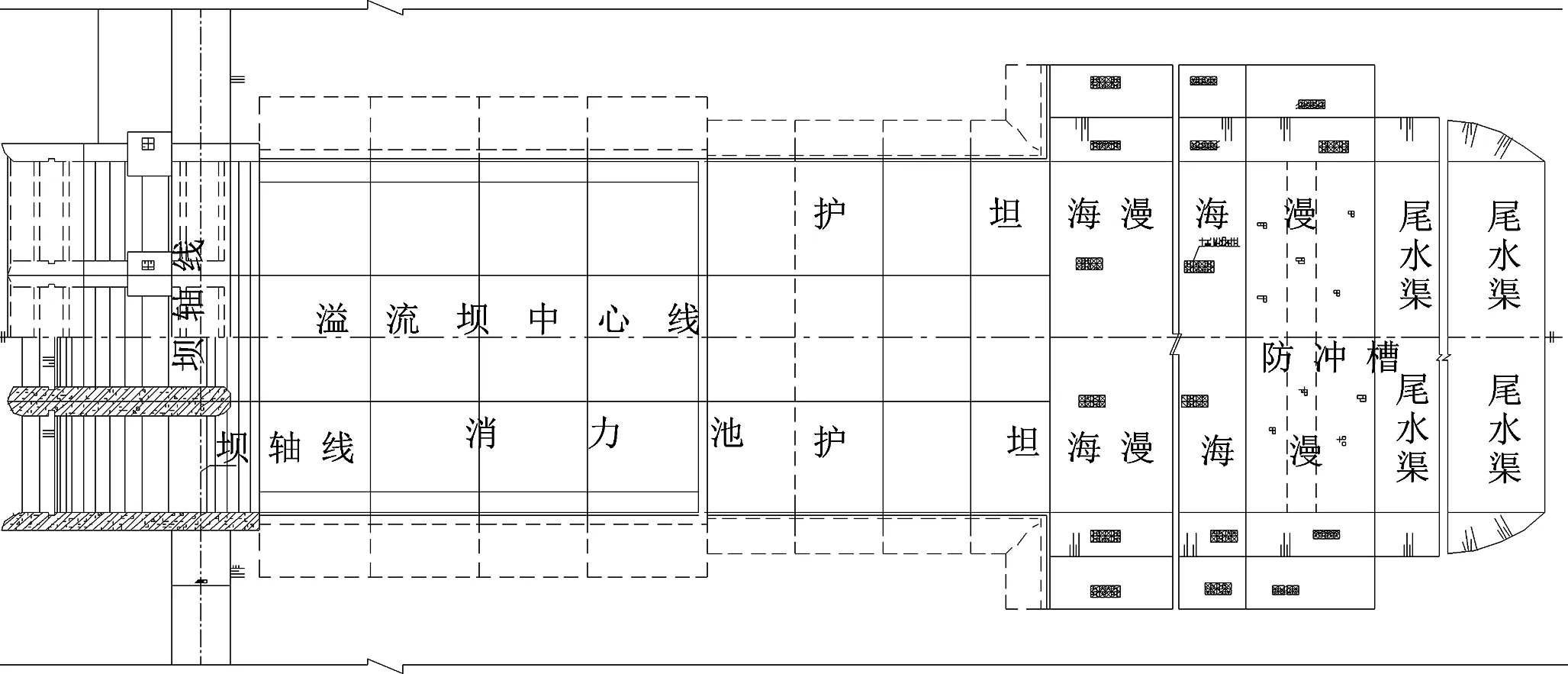
图1 溢流坝平面布置示意

工程主要特征水位及泄量见表1，泄洪操作时可将所有闸门按同一开度开启，也可只开启部分闸孔以调节下泄流量，但要尽量对称开启以利下游流态稳定[9]。

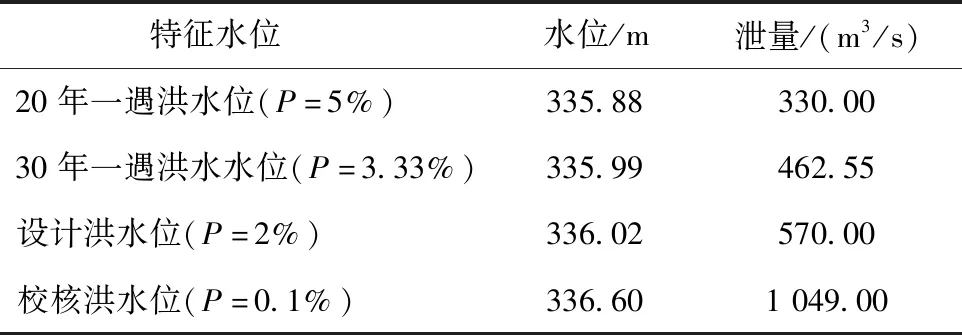
表1 溢流坝主要特征水位及泄量

该工程由于消力池出口原河道宽阔，泄流时下游水深较浅，故本次消力池结构尺寸设计较大。在消能设计过程中，对溢流坝进行了水工模型试验，主要针对20年一遇洪水、30年一遇洪水、设计洪水、校核洪水4个试验工况进行试验，分别检验溢流坝水流流态、流速分布以及压强分布情况，对消能建筑物结构进行了优化，达到节省建设投资的目的。最终采用数值模拟的方法对优化设计方案进行检验，为优化设计提供充足的依据。

3 数值模拟

3.1 数值模拟方法

物理模型试验和数值模拟是水力学研究的主要方法。由于水流流态复杂，模型试验是有效的研究方式。模型试验按照相似原理和相似准则，将原型实物按照一定比例缩小，通过试验的方法预演或重演并据此判断。通过模型试验可以对水力现象进行系统的观测研究，为理论分析提供依据。随着计算机技术的快速发展，数值模拟的方法被广泛采用，基于CFD数值模拟(计算流体动力学模拟)是以流体流动的质量守恒方程、动量守恒方程、能量守恒方程等基本方程来研究并模拟流体的流动情况。通过CFD的这种模拟，可以解决各种流体流动与传热问题，已经成功应用于各个领域。在计算机上通过数值模拟就可以形象再现物理试验的流动情景[10-12]。

CFD商业软件FLUENT，是通用CFD软件包，可以模拟从不可压缩到高度可压缩范围内的复杂流动，本文采用FLUENT软件对溢流坝进行数值模拟来研究其水力特性[13]，其中水流的自由液面通过VOF(Volume OF Fluid)方法进行分析。VOF方法是建立在欧拉网格下的界面追踪方法，该方法中，互不相容的流体组分共用一套动量方程，并通过引入相体积分数这一变量来实现对计算域内相间界面的追踪。

采用FLUENT软件分析时还需要选择湍流模型，FLUENT软件中采用的湍流模拟方法有Spalart-Allmaras模型、标准模型、RNG模型、Realizable模型、RSM模型及大涡模拟方法。由于Realizablek-ε模型在模拟强逆射流扩散率、压力梯度、回流、分离等问题上有较高的精度，而且收敛速度也较快，因此计算中采用Realizablek～ε双方程紊流模型，并对控制方程用有限体积法进行离散[14-17]。为了简化求解过程，获得相对准确的计算结果，在CFD中需选择合适的离散格式将方程离散成代数方程，在对其方程进行计算时，将方程中未知量的求解顺序等进行一些特别的处理，将偏微分方程组转化为空间网格的各节点的代数方程组，然后通过对代数方程组的求解来得到这些节点的值，而其他位置的值则可以根据插值原理等求出，其插值方式就叫做离散格式。本次数值模采用了QUICK格式的离散格式，并且选择了在流程的数值计算方法中针对非稳态下的可压流动的PISO方法。

在恒定计算过程中，计算的结束是以所有计算变量的残差值小于或接近10-5，并保持稳定或者水流的进口质量流量与出口质量流量相等作为判断标志。

3.2 模拟范围及网格划分

该溢流坝段包括控制堰段、消力池段、护坦段等组成，具体布置见图2。为观察完整流态，模拟范围向上延伸25 m，向下游延伸50 m。

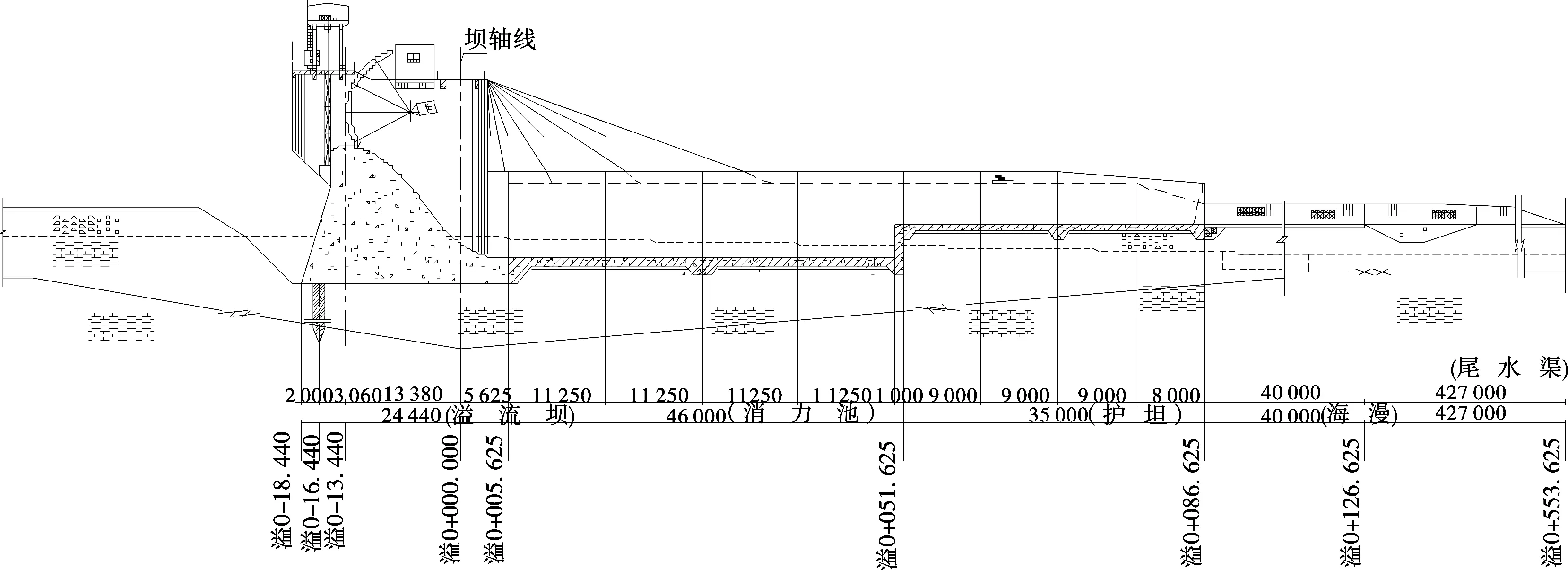
图2 溢流坝段纵断面示意

由于模拟的坝体段体型较复杂，采用AutoCAD建立模型，其大小采用原型尺寸建立。建立二维模型后，把模型输出到前处理软件GAMBIT，进行划分网格。网格的划分对于数值计算非常重要，质量不高的网格会降低模拟的精度，甚至会导致模拟的失败，在该模型中使用的网格单元类型为四边形网格，网格尺寸为0.5 m(溢流坝的网格划分如图3所示)。

图3 模型部分网格及尾水段网格示意

3.3 数值模拟结果

在该计算中，上下游水位保持不变为常量，在稳定后，其流态与时间无关，所以此计算是个稳态问题。在计算中设立了7个监测点(x1、x2、x3、x4、x5、x6、x7)和2个监测断面(通过进出口质量流量相等验证计算结束)，其位置如图4所示。

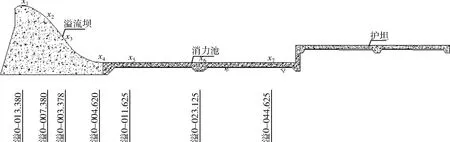
图4 数值计算监测点位置示意

1) 计算工况。由于在校核洪水下，水流流速最高，水汽交界面最为复杂，因此选取最不利条件下(校核洪水)的计算工况，其他工况不做检验。在此工况下，针对消力池深4.0 m，其上游库水位为336.57 m，下游尾水位325.00 m，流量Q=1 053.30 m3/s。通过物理模型试验中相应点的压力和CFD数值模拟溢流坝段监测点的压力对比见表2。

由表2可见，模型试验中测点压强大小较数值模拟的偏小，其原因可能是由于数值模拟在边界处理上不能与实际完全相符，以及数值模拟过程中对复杂问题进行了简化。但在数值模拟允许范围内，试验的结果也在一定程度上验证了数值模拟的准确性。

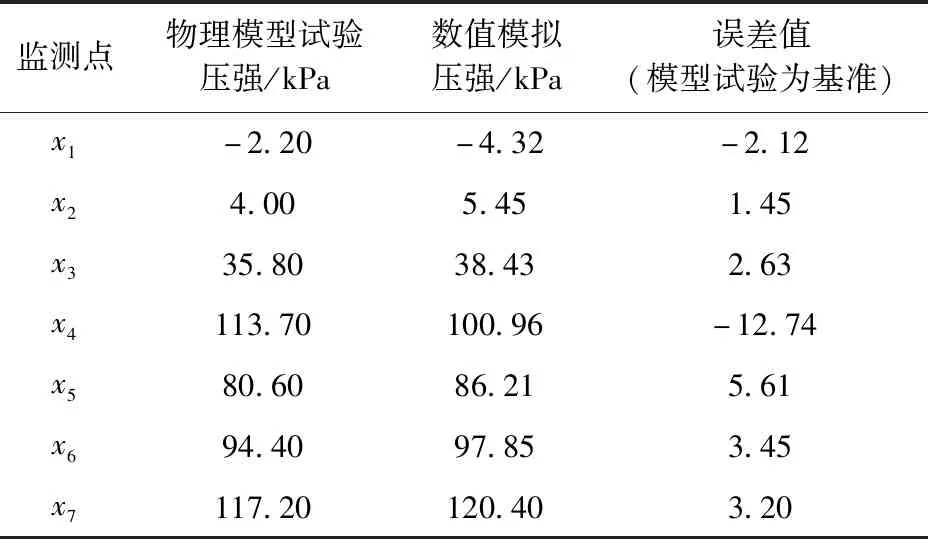
表2 监测点压强分布

2) 数值模拟分析。利用VOF模型跟踪自由水面，可看到明显的水汽交界面(模拟区域内密度分布结果如图5所示)。

图5 数值计算区域内密度分布示意

从图5中可以看出，发生了淹没式水跃，水汽混掺充分，在消力池中水流湍动强烈。

在图6可以看出，溢流坝顶部及消力池两端流速较小，产生回流的区域，对消能是有利的；图7可明显看出在溢流坝顶部产生了负压。

图6 数值计算区域流场分布示意

图7 数值模拟区域压力分布示意

从数值模拟的结果看，上游及下游没有出现明显的水面线波动的现象，水流较为平稳，符合水流的运动规律和力学特性，此方案的消能效果较好，与试验结论相符。

4 结语

泄水建筑物是水利水电工程枢纽中的重要组成部分，要结合具体的地质、施工、水文等条件和运行要求，本着既安全又经济的原则选定具体布置及形式。团山子水利枢纽采用在右岸布置溢流坝的布置方式，采用应用较多的WES型堰面形状。

尽管数值模拟方法的准确性还有待提高，无法仅仅以数值模拟的结论作为设计的依据，但是数值模拟方法的部分结果可以更形象的对其特性进行表述。本文利用FLUENT软件中的VOF模型对溢流坝进行数值模拟，研究其特定工况下的水力特性。首先用AutoCAD建立了溢流坝段体型模型，输入前处理软件GAMBIT对其进行网格划分，在设置边界条件后，利用FLUENT软件中的VOF模型获取了溢流坝校核水位工况下特定点的压力分布，并且跟踪自由水面，计算得到了模拟区域内密度分布。对比模型试验数据与数值模拟的计算结果，两者吻合较好，与设计值符合，说明下游消能效果较好，模型试验数据是可靠的，优化设计方案是可行的。