斜波压缩下锡的相变和层裂行为1)
2023-02-25种涛莫建军傅华李涛罗斌强
种涛 莫建军 傅华 李涛 罗斌强
(中国工程物理研究院流体物理研究所,四川绵阳 621900)
引言
武器、航空航天飞行器、汽车等工程结构受到内爆加载、高速撞击等动态载荷时会发生相变、层裂等现象,因此相变、层裂损伤及两者的相互关联研究是国防工业、基础科研的热点问题.锡是低熔点低强度[1]金属,具有丰富的相结构,常被做为相变和损伤研究的典型材料.相图中锡有4 个固体相和1 个液态相,针对其复杂的相结构人们已开展了实验[2-6]和理论[7-12]研究.静高压实验观测到锡的β-γ相变压力约9.4 GPa[13-14],且伴随约−2.6%的体积间断[3,15-17],说明β-γ 相变为一级相变.锡在约40 GPa[4-5]时开始γ-bcc 相变,此相变会造成约−0.76%[1]体积间断.冲击加载实验中,锡的卸载熔化和冲击熔化压力分别为23 GPa 和49 GPa[14].Davis 等[18]利用Z 装置完成了锡的斜波压缩实验,速度波剖面出现了β-γ 相变对应的特征波形,Davis 还基于Hayes 多相模型[19]开展了数值计算工作,计算结果不能很好描述相变过程.种涛等[20-21]开展了锡的斜波加载实验,也获取了含有β-γ 相变信息实验结果,与Davis 结果基本吻合.文献[13,22-23]先后开展了锡的多相Gruneisen 模型研究,Khishchenko[24]构建了锡的多相自由能模型,Zhang 等[25]建立了锡的β 和γ 两相的完全物态方程.利用考虑了包氏效应的多相本构模型,Song 等[26]对锡的冲击实验开展了数值模拟研究,计算结果可以很好地描述实验加载和卸载过程.
目前学者们利用静高压和冲击加载技术开展锡的相变行为实验研究,利用冲击加载技术开展锡的层裂损伤研究,斜波加载实验技术在材料相变动力学研究方面具有优势[21,27],但是斜波压缩下锡在卸载段是否发生层裂现象,若发生与冲击加载下层裂是否有所不同这一物理问题并不清楚.本工作采用斜波加载实验技术,同时开展锡相变、层裂的实验和数值模拟研究.结合由锡的多相Helmholtz 自由能计算的多相状态方程、Hayes 相变动力学方程和损伤度理论,对斜波压缩实验过程进行一维流体动力学数值模拟.
1 斜波压缩实验设计
CQ-4 是紧凑型磁驱动加载装置,可输出上升沿400~ 600 ns、峰值约4.0 MA 的光滑脉冲电流[28].实验负载区结构见图1 所示,加载电流通过由两个极板组成的U 型回路,在两电极板之间的缝隙产生感应强电磁场,电磁场再与加载电流相互作用产生垂直于载流面、向外的洛伦兹力,即磁压力,磁压力通过加载电极板传入样品.为了保证锡样品在实验过程中一维应变且其内部不形成冲击波,需对实验负载区结构和具体尺寸进行设计,具体方法见文献[21,29].本文实验的负载区结构布局及磁驱动加载原理示意图如图1 所示.实验有四个测速位置,其中三个位置测量不同厚度锡的后表面速度,一个测量极板Al/LiF 窗口界面速度.实验主要条件见表1.
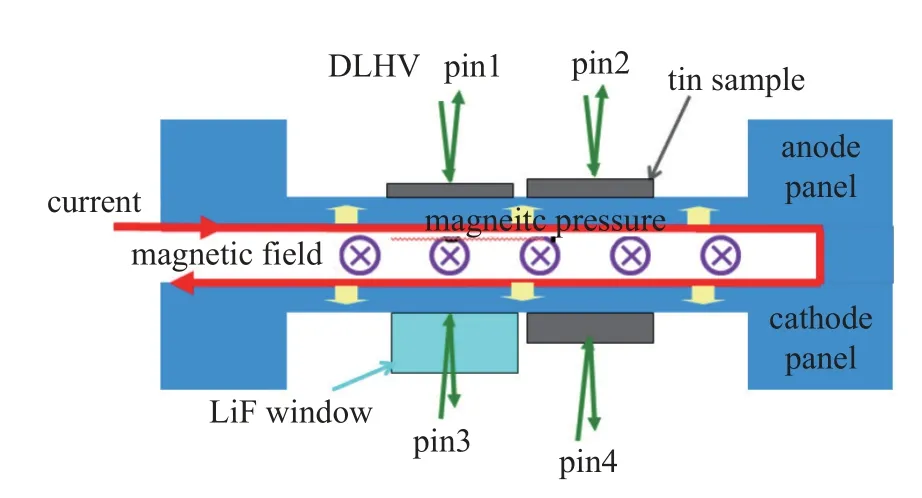
图1 磁驱动加载原理及样品布局Fig.1 Schematic diagram of magnetically driven ramp wave loading and layout of the samples

表1 实验条件Table 1 Experimental condition
2 实验结果与分析
图2 为实验获取的三个锡样品和铝极板后表面速度波剖面数据.其中图2(a)为加载电极铝/LiF 窗口界面速度,与实验加载电流波形相似、都近似正弦波,这是由装置放电参数决定的[28].由图2(a)得,速度5%到95%上升沿约600 ns,从1.16 μs 开始出现了较强的卸载、速度急剧下降,这是由于内表面卸载稀疏波到达Al/LiF 界面造成的,速度峰值到卸载时间T01≈ 0.27 μs.

图2 实验速度曲线Fig.2 Experimental velocity curve
图2(b)为不同厚度锡样品后表面速度波形,三个波形大体相同,只是进行了时间上的平移,随着进入锡样品中应力波压力的提升,速度波形平滑上升,加载段先后出现了弹塑性转变和相变对应的特征波形,卸载后又出现了由层裂损伤造成的振荡特征波形.图中弹塑性转变、相变和层裂三个物理现象对应的特征值具体见表2.三种厚度锡样品弹塑性转变对应的特征速度基本一致、约40 m/s,计算得到屈服强度约0.194 GPa,与冲击实验结果基本吻合[30].随着锡样品厚度的增加,相变对应的特征速度从670.3 m/s 减小到639.0 m/s,相变起始压力从7.54 GPa 减小到7.14 GPa,这是由于相变波在薄的样品中还处于非稳定态,变化趋势与冲击实验结果吻合.在卸载区,三个厚度样品第一个振荡周期(T)大致相等约0.29 μs,可得层裂片厚度δ≈C0T/2=2.59 × 0.29/2=0.38 mm.由图可提取三个锡样品峰值速度和回跳速度,两者之差为回拉速度(Δu),由层裂强度计算公式σs=ρ0C0Δu/2 可得其层裂强度约1.1 GPa,相同加载压力峰值下,冲击实验中锡的层裂强度约0.65 GPa[31].冲击加载下锡的层裂强度低,首先是由于冲击应变率高、相同加载压力下引起的冲击温升大于斜波压缩过程,本文斜波压缩实验15 GPa峰值压力下锡的温升约50 °C,而15 GPa 冲击加载下锡的温升约200 °C.其次,冲击实验中的锡后表面会反射强卸载冲击波,强卸载冲击波也会造成巨大的温升,实验发现20 GPa 附近卸载冲击波会造成锡卸载熔化,导致其层裂强度快速减小.

表2 速度波剖面上的特征值Table 2 The typical characteristic physical variables in the wave profiles
3 数值模拟与分析
为了再现本实验中锡的弹塑性转变、相变和层裂这三个物理过程,数值模拟需要同时考虑弹塑性模型、相变速率方程、多相状态方程和损伤模型.本文采用率相关的非平衡相变动力学方程、基于Helmholtz 自由能的多相状态方程和基于材料微观损伤的材料损伤演化方程来描述相变和层裂两个物理过程.由于实验过程为一维应变,数值模拟采用自编的一维流体动力学程序完成.
锡的本构关系采用Steinberg 模型[30],由于锡强度较低,对相变和层裂两个物理过程影响较小,因此本文忽略锡两相强度的差异,模型及其参数两相相同,初始屈服强度由本文实验结果确定.由实验结果得,锡的相变是在一定时间内完成,因此本文采用Hayes 非平衡相变速率方程[19,21],相变弛豫时间与Hayes 多相状态方程数值计算时的值[20]相等.
3.1 锡基于Helmholtz 自由能的多相状态方程
在一定比容V和温度T下,锡的Helmholtz 自由能[23]具体表达式为
式中,三项依次为固体的结合能、晶格的振动自由能和电子的自由能.
第一项固体结合能只是比容的函数,其具体形式为
式中,VR为参考比容,BR和为分别为绝对零度时固体在参考比容处的体积模量及体积模量对压强的一阶导数,PR为参考比容时的压强,Φ0(VR)为参考比容时的结合能.
第二项晶格的振动自由能在准谐振子近似下,具体形式为
式中,N为固体单位质量的原子数,kB为波尔兹曼常数,Θ (V)为德拜温度,D(z)为德拜积分.
第三项电子的自由能的具体表达式为
确定锡的β 和γ 两相Helmholtz 自由能表达式具体形式后,由热力学关系可计算锡在给定热力学状态下各相的压力和熵,其表达式为
式中,i=β 或γ,Pi为各相的压力,Si为各相的熵.
联立式(1)~ 式(5),可获得锡基于Helmholtz 自由能的多相状态方程,具体表达式为
锡的β 和γ 两相Helmholtz 自由能参数具体见表3.表中Φ0(VR)需要说明,数值模拟中需要的是两相参数的差值,并不需要每一相的准确值.

表3 锡的Helmholtz 自由能参数[20-21,23]Table 3 The parameters of Helmholtz free energy of Tin[20-21,23]
3.2 损伤演化方程
为了联系微观损伤理论和宏观物理模型,建立了损伤度(D)这一内变量,其定义为含空穴介质中空穴体积(Vold)与总体积(Vol)之比,其定义式为
式中,Vols为实体物质体积.
本文损伤演化方程采用袁福平[32]建立的适用于延性金属材料的损伤模型,该模型同时考虑了空穴成核和生长两种因素对损伤演化的贡献,具体形式为
式中,N和a分别为空穴成核和空穴长大损伤因子,σs为微损伤处拉应力,σ0为空穴成核和长大的阈值应力,λ为损伤率对相对阈值应力的依赖指数.
假设材料发生宏观层裂的极限损伤值为Dc,层裂条件可写为
当损伤达到极限损伤的时候材料发生层裂.结合式(8)和式(9)可开展材料中微损伤的演化和层裂发生的描述,锡的损伤演化模型具体参数见表4.其中 σ0与实验结果计算的层裂强度相当,Dc由实验结果确定.

表4 锡的Steinberg 模型[20,30]和损伤演化方程参数Table 4 Steinberg model[20,30] and damage evolution equation parameters of Tin
损伤度大于零后,需要对压力和强度进行修正,具体形式为
式中,P和Y分别是不考虑损伤时计算的压力和屈服强度,PD和YD分别是损伤度修正后的压力和屈服强度.
3.3 数值计算结果
数值模拟以铝极板内表面压力历史为边界条件,结合Al/LiF 界面速度数据和反积分数据处理方法可获取压力历史,见图3(a),加载压力峰值约15 GPa,波形上升沿约550 ns.由压力边界计算的Al/LiF 界面速度波形与实验结果重合,验证了该方法的正确性.图3(b)为计算和实验速度波形,三个样品的计算和实验结果整体吻合,计算结果可以很好地再现斜波压缩下锡样品依次经历的弹塑性转变、相变和层裂三个物理过程,其中计算波形中的弹塑性转变对应的特征速度、相变起始对应的特征速度、速度峰值、层裂对应的回拉速度及层裂片中应力波振荡周期等关键数据都与实验结果吻合,验证了物理模型及其参数的正确性.需说明,虽然实验过程包含了三个物理过程,但三个物理过程对应的物理模型及其参数并非强关联.锡的强度有一定的硬化效应,但其最大值小于0.25 GPa,对7.5 GPa 附近的相变过程和15 GPa 峰值压力后卸载段的层裂过程影响基本可以忽略.通过数值计算人为控制相变发生,分析相变对层裂强度的影响,发现相变对锡的层裂强度影响很小,结合冲击实验结果说明锡层裂强度的主控因素是温度.
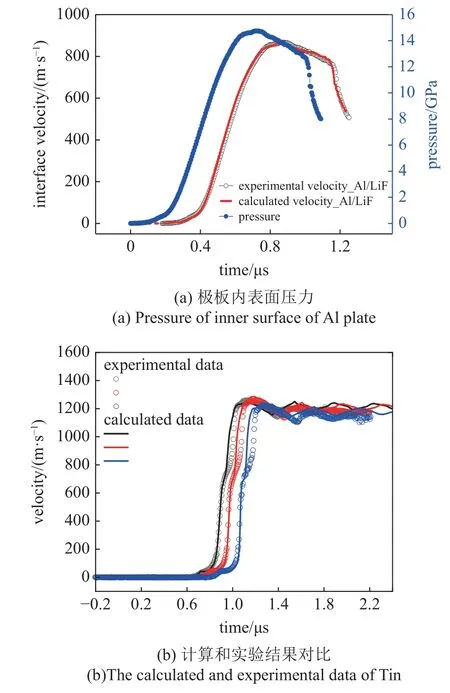
图3 计算和实验数据Fig.3 The calculated and experimental data
图4(a)为1.51 mm 厚锡样品加载面附近中心点的两相质量分数演化图,相变速率模型中的相变弛豫时间为6 ns,计算结果得在相变前全部为初始β 相,从相变起始压力7.5 GPa 开始,逐渐出现新相γ 相,γ 相质量分数随着样品中压力的提高逐渐增加,说明锡的β-γ 相变是率相关的非平衡相变.图4(b)为以本文物理模型计算的高压声速−压力曲线与其他计算或实验结果,本文数据依次出现了弹塑性转变、相变对应的声速变化,其中起始阶段声速从3.3 km/s 快速降低到2.6 km/s 对应的弹塑性转变,随后应力波以体波声速传播,在约7.5 GPa 处声速减小是由β-γ 相变造成的体积间断引起的,相变后应力波恢复到体波声速传播.本文计算的高压声速数据和其他文献数据整体趋势相同,都出现了相变引起的声速波动,本文计算声速和文献[22]计算的体波声速数据相近,但是相变完成后两者有一定差异,这是由于物理模型及其参数不同.
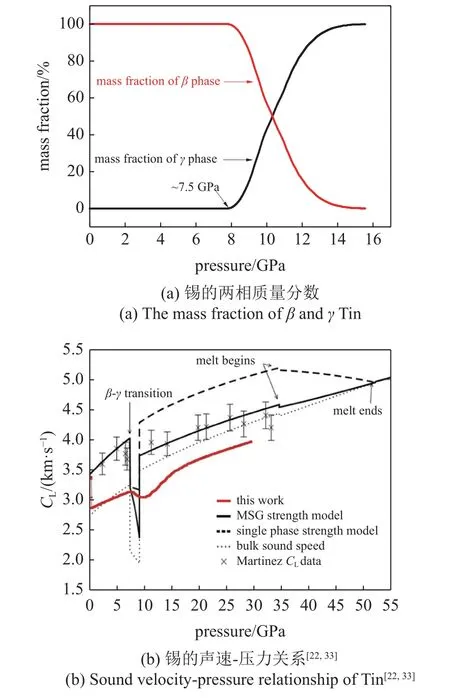
图4 数值计算结果Fig.4 The calculated data
由于斜波加载实验中对样品进行连续的压缩,单发实验可获取样品从初始状态到终态的准等熵线.图5(a)为在压力−比容热力学平面本文计算的准等熵线与等温线、冲击Hugoniot 实验数据对比,相变前、7.5 GPa 以下低压段等温线、冲击绝热数据和准等熵线基本重合,与理论预估吻合[38].相变开始后,本文计算的准等熵线与等温线数据基本重合、都位于绝热冲击数据下方,这是由于斜波压缩过程无强的间断面出现、样品中温升低.图5(b)为在温度−压力热学平面相图中本文计算的准等熵线路径和冲击绝热线路径,对比得斜波压缩过程中样品中的温升明显小于相同压力下的冲击加载过程,且两种情况下的温度差异随着压力的增加而变大.温度的差异是造成冲击和斜波加载下锡层裂强度巨大差异的主要原因.
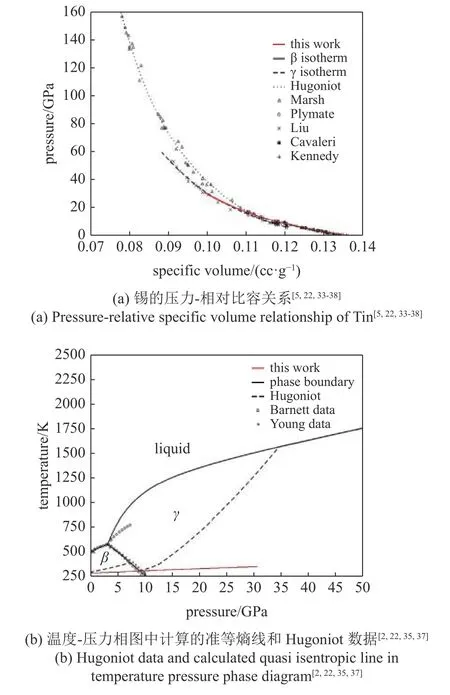
图5 不同热力学平面锡的等熵线Fig.5 Quasi isentropic lines of tin in different thermodynamic planes
4 总结
利用电磁加载CQ-4 装置,开展了锡的动态实验研究,首次在斜波压缩实验中获取包含弹塑性转变、相变和层裂三个物理行为信息的速度波剖面数据.实验结果显示,锡的屈服强度约0.194 GPa,相变起始压力随着锡厚度的增加从7.54 GPa 减小到7.14 GPa.在卸载段出现了明显的层裂损伤,层裂强度约1.1 GPa,与相同加载压力下冲击实验结果有巨大差异.结合由锡的多相Helmholtz 自由能计算的多相状态方程、Hayes 相变动力学方程和损失度理论,对金属锡的斜波压缩过程进行了一维流体动力学数值模拟,计算结果可以很好描述锡的弹塑性转变、相变和层裂三个物理过程.
致谢
感谢吴刚、胥超、税荣杰对 CQ4 实验装置的运行和邓顺益在实验数据测试中的帮助!
