基于优化核极限学习机的泥石流危险性评估
2023-02-25尚艳芳李丽敏温宗周王朝阳夏梦凡
尚艳芳, 李丽敏, 温宗周, 王朝阳, 夏梦凡
(西安工程大学电子信息学院, 西安 710600)
中国地形地貌较为复杂,其中山区地形所占比例占70%,且处于地震多发带,再加之不合理的工程活动,使中国山区居民饱受泥石流灾害的困扰,泥石流灾害破坏力巨大,容易导致大量人员伤亡和经济损失。因此,采用科学、先进的泥石流危险性评价方法,建立有效的预测预报系统是非常必要的。
针对泥石流危险性评价的研究开始较早,已取得较为丰富的成果,并且,随着泥石流的研究不断深入,各种其他学科理论和方法不断引入泥石流研究领域,中外许多学者对泥石流危险性评价也有了更透彻认识。李丽敏等[1]针对泥石流多因素影响,提出最小二乘支持向量机的泥石流灾害预报模型,但模型输入多维数据,计算机占用较多时间资源和内存资源,造成网络迭代速度较慢。根据泥石流形成条件不同,邓恩松等[2]针对两大不同类型的(降雨型和冰川型)泥石流进行研究,以中巴公路奥布段为研究区,结合了主成分分析法和灰色系统理论建立评估模型,但此种研究方法只适用于降雨型和冰川型泥石流灾害预测,具有一定的局限性。王俊豪等[3]使用层次分析法来确定泥石流危险性评价中各影响因素的权重,通过引用多位专家的评判标准减小主观误差对结果的影响,但没有进行进一步的验证性分析,可能导致多变量之间相互叠加,影响预报准确性。王艳锦等[4]使用特征金字塔网络对成康铁路沿线泥石流进行危险性评估,研究结果表明了机器学习理论在突发性地质灾害领域的有效性和可行性。张晓东[5]以宁夏盐池县作为地质灾害研究区,使用遥感和多源信息融合技术进行泥石流危险性评价,这一方法虽然效果较好,但由于需要借助遥感技术,因此不具有普适性。王晨辉等[6]采用支持向量机模型预测泥石流的危险程度,有大量数据可以供模型训练学习,这种方法虽然精度得到了保证但模型建立过程复杂,计算量较大。
针对上述预测方法中存在的问题,现采用主成分分析(principal component analysis,PCA)线性降维算法,对数据集做特征压缩;之后,使用核极限学习机(kernel based extreme learning machine,KELM) 预测泥石流危险性,并利用萤火虫算法(firefly algorithm,FA)对其进行参数寻优,从而得到泥石流危险性的分类结果;最后,将本文方法与核极限学习机模型、多分类支持向量机模型和BP(error back propagation,BP)神经网络模型进行比较,验证FA-KELM模型的优越性。
1 研究方法介绍
1.1 主成分分析算法(PCA)
主成分分析(PCA)采用几个互相正交的变量信息代替多源的信息量,目的是以最少的新变量揭示原可观测指标,在数据特征压缩的同时,最大程度避免特征信息间重叠,尽量减少原指标包含信息的损失[7-8]。包含如下步骤。
(1)设i组j维变量构成的数据矩阵为
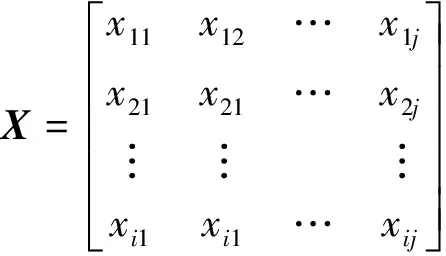
(1)
式(1)中:xij为j维变量的第i个样本,将xij标准化处理,得
(2)
(2)计算相关系数矩阵R。
R=[rij]m×n
(3)
(3)计算累计贡献率βi。
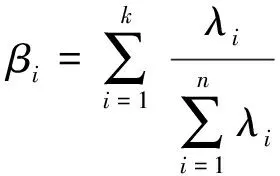
(4)
式(4)中:λj为特征矩阵R对应的特征值。
(4)选定主成分个数。一般情况下,当累计贡献率不少于85%时,则选定有m维主成分[9],与之对应的有m个特征值Λm=diag[λ1,λ2,…,λm]和m个特征向量Wm=[w1,w2,…,wm]。
1.2 核极限学习机(KELM)
核极限学习机(KELM)和其他传统前馈神经网络的结构类似,但在训练学习时,所需迭代参数少,学习速度快,其输出样本函数F(x)可用矩阵[10]表示为
F(x)=h(x)β=Hβ=L
(5)
β=H*L
(6)
式中:x为给定的模型输入因子;h(x)、H为隐含层神经元的输出;β为隐含层和输出层之间的连接权重;L为网络学习后的期望输出;H*为H的广义逆矩阵。通过求解最小二乘解[式(7)]可以得到输出权重矩阵的结果。

(7)
式(7)中:I为单位矩阵;C为正则化系数;本文研究中的核函数选用高斯核函数,即
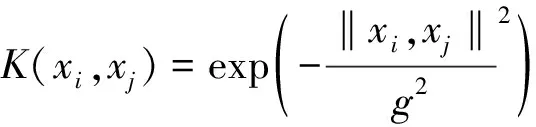
(8)
式(8)中:g为核参数;xi、xj为模型输入因子,引入核函数后,核矩阵为
QELM=h(xi)·h(xj)=K(xi,xj)
(9)
则表达式(5)网络输出可描述为
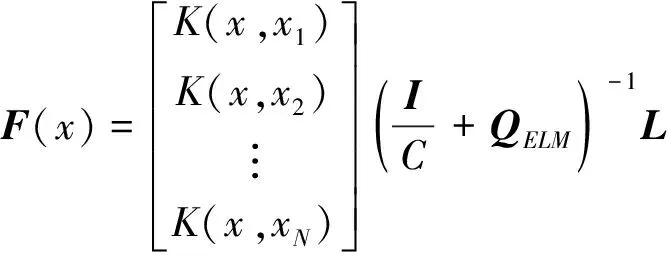
(10)
1.3 基于FA算法训练KELM模型
虽然KELM算法克服了传统ELM算法的缺点,但基于核的ELM则存在模型参数选择问题,本文研究中通过萤火虫算法[11-12](firefly algorithm,FA)调整KELM模型中的超参数,解决因人工设置参数而导致预测结果的随机性和不确定性,提高建模精度和预测性能。该模型的训练过程如表1所示。
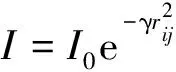
(11)
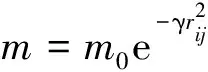
(12)
rij=‖xi-xj‖
(13)
式中:I0为最大亮度;m0为最大吸引度;γ为光强吸收系数;xi和xj分别为萤火虫个体i和j的所在位置。个体i向另一个个体j空间转移的依据公式为

表1 FA算法训练KELM模型过程Table 1 FA algorithm training KELM model process

(14)
2 研究区概况
北川县坐落于四川省盆地西北部向川西高原的过渡带上,峰峦起伏,山地自然景观占全县一半以上的面积,沟壑纵横,季风气候明显,阴雨天气较多,年均降雨量1 399.1 mm,空间分布不均,具有东南向西北变小的规律[13],同时,区内最高海拔4 769 m,最低点540 m,不稳定沟床比有明显规律,易于泥石流输移,流域切割密度较大,使得固体物源更易于参与泥石流活动。根据唐川等[14]、汪月鹃[15]调查,该区域内相对高差超过1 000 m,沟谷斜坡坡度多为15°~40°,地形险峻,地层岩性多样,复杂的地质构造为流域的支沟发育和泥石流的发生提供有利条件(图1)。
3 建模过程和结果分析
3.1 数据预处理
本文中数据摘自四川省北川县国家重点地质灾害监测项目的历史数据,选取其中72条泥石流沟基础数据作为研究样本。综合《泥石流危险性评价》[16]等,最终选择8种初始影响因子,分别为流域切割密度X1、流域面积X2、流域相对高差X3、不稳定沟床比X4、松散固体物质储量X5、年均降雨量X6、地震烈度X7和主沟长度X8。
为了克服输入影响因子丢失或者异常值对地质灾害预报准确性的影响,分别针对噪声大、存在野值、数据种类多的问题,使用以下3种方法进行解决。
(1)适当滤波法。本文使用移动平均滤波器对原始数据进行平滑处理,使用smooth函数,设置移动平均滤波器的默认窗宽为5。
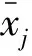
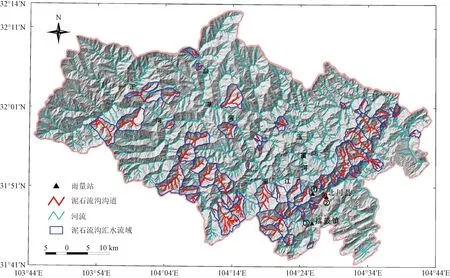
图1 北川县泥石流分布图Fig.1 Debris flow distribution map in Beichuan County
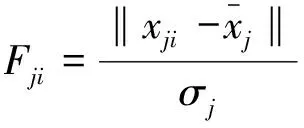
(15)
若Fji>F(n,a),则判定该数据属于异常值,应该丢弃对应的数据xji。
(3)归一化。在本数据集中有8种数据,为避免对后续变量的运算和分析造成很大的干扰,加快模型的求解速度,得到合理的结果,将所有纲量映射至[0,1]区间。转换函数公式为
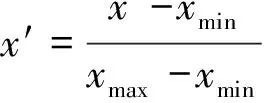
(16)
式(16)中:x′为经过归一化后的数据;x为样本原始数据;xmax、xmin为样本数据中的最大值、最小值。
为了验证预处理方法在本模型中的有效性,将预处理前后的数据分别作为FA-KELM预测模型的输入,对比了数据预处理前后的分类结果,如图2 所示。
从图2对比结果可知,通过必要的预处理工作,剔除了异常值,数据的取值范围均在客观合理范围内,模型预测准确率达到90.47%;然而,把不规范的数据作为输入时,其预测准确率仅有71.42%。仿真结果表明,在数据输入模型前,确保数据格式一致化以及数据的完整性是十分有必要的。

图2 数据预处理前后FA-KELM模型预测结果对比Fig.2 Comparison of FA-KELM model prediction results before and after data pretreatment
3.2 PCA降维
在数据集中随机选择51条泥石流沟数据作为网络模型训练,剩余数据用于验证模型。选择累计贡献率不少于85%的成分作为主成分,利用PCA算法选择出4种综合指标,涵盖了8个原始指标体系的绝大部分信息,达到了数据信息精炼化,提取后的变量如图3所示,将线性组合后的新变量输入到FA-KELM模型中进行训练学习并验证,降维前后的测试时间分别为100.69、82.47 ms。有效提高KELM模型的学习能力。
由图3中PCA主成分提取变量结果可得,前4个成分的累计贡献率为45.428%、63.297%、76.132%、86.259%,且到第4个成分时的累计贡献率达到了86.259%,大于定义主成分临界值85%。因此利用PCA主成分分析法能够将初始8维变量数据降至4维,模型数据结构复杂度控制到更低且消除了各因子之间的相关冗余度。所得到的主成分系数矩阵如表2所示。
根据表2中主成分系数矩阵可得,原始变量和主成分之间的线性关系表达式为
(17)

表2 主成分系数矩阵Table 2 Principal component coefficient matrix
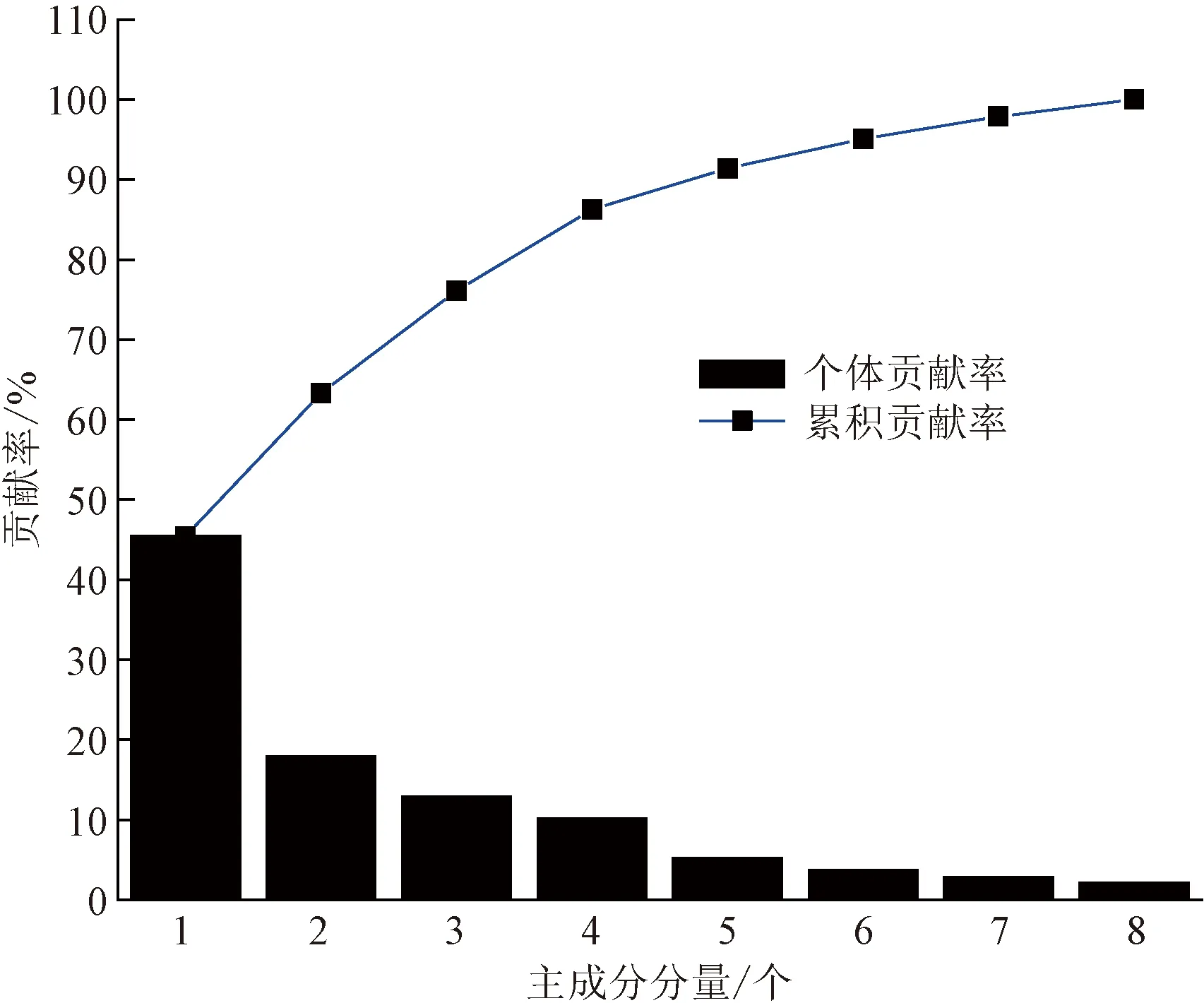
图3 PCA主成分提取变量Fig.3 PCA principal component extraction variables
式(17)中:F1~F4为降维后的4维主成分变量;X1~X8为原始8维影响因子数据。
3.3 仿真验证及结果分析
3.3.1 参数选择
KELM算法性能优劣取决于惩罚系数C和核函数参数g的选择,利用FA优化算法对以上参数进行优化选择,分类器的惩罚系数和核参数优化范围设置为(C,g)∈[2-5,210],为避免实验的偶然性且计算量适中,种群规模n设置为35,最大迭代次数为50,得到的最优参数C和g分别为142.413和1.802,优化参数花费时间为21.62 s,图4为寻优算法适应度值曲线图,萤火虫算法以极快的收敛速度取得更高的适应度函数值,寻优效率高,整体收敛能力强。基于Python3.7以及MATLAB2017b进行编程实现网络模型和优化算法,CPU为Intel(R) Core(TM) i7-10700F CPU@2.90 GHz,RAM为16.0 GB。

图4 寻优算法适应度曲线Fig.4 A chart of the adaptability curve of the optimization algorithm
3.3.2 评估模型训练
首先通过PCA对泥石流数据做特征提取,将训练集和测试集按3∶1划分,并且将危险性划分为4个等级,分别为: 低度危险、中度危险、高度危险、极高危险,其级别分别对应1级、2级、3级、4级。基于FA-KELM的泥石流危险性预测模型的流程如图5所示。初始时,使用随机产生的参数作为FA的初始种群,将训练集输入FA-KELM网络进行训练。预测准确率作为个体适应度函数,为去除较差子群,更新萤火虫位置,以最大适应度函数为标准选择,使得模型获得最佳调优的参数,最后利用测试集测试该模型的准确性。
3.3.3 性能评估
选取在泥石流预测方面应用较为广泛的核极限学习机[17](kernel based extreme learning machine,KELM)、多分类支持向量机[18-19](multi-class support vector machine, MSVM)以及误差逆传播算法[20-21](error back propagation,BP)作为对比模型,并采用混淆矩阵、曲线下面积(area under curve, AUC)、ROC曲线(receiver operating characteristic curve, ROC)评价分类器性能,在相同条件下FA-KELM模型与预测模型进行效果对比。图6和图7给出了各对比模型在相同数据集下泥石流危险性分类的混淆矩阵和ROC曲线。
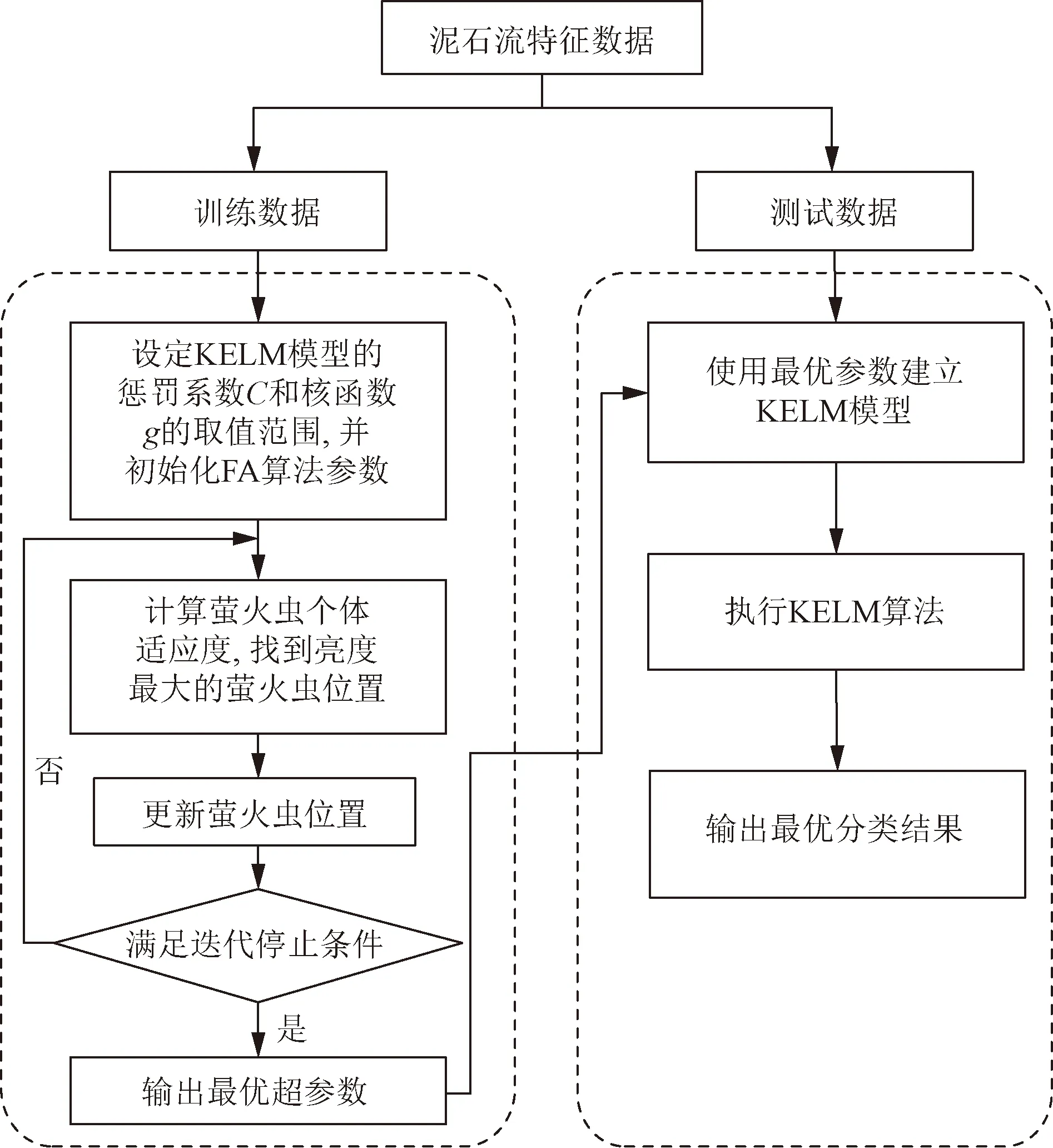
图5 基于FA-KELM的泥石流危险性评价流程图Fig.5 Flow chart of debris flow hazard assessment based on FA-KELM
由图6对比可知,本文提出的模型在对角线上的值均高于其他模型在对角线上的值,得到最佳混淆矩阵,KELM预测性能稍好,MSVM算法的预测标签与真实标签之间存在较明显的出入,BP算法预测结果偏离实际泥石流危险性等级,并且预测模型的优劣与ROC曲线下方面积的大小有关,面积越大,说明模型表现出色,根据图7的ROC曲线结果可知,FA-KELM曲线的面积为最大,对角线代表分类能力为0的一条线,ROC曲线离对角线越远,AUC越大,表明模型的分类能力越强。各模型具体AUC如表3所示。
根据表3对比可知,本文提出的FA-KELM模型在ROC曲线下面积AUC均值为90.6%,因此,与其他网络相比,其拥有最大AUC 均值,说明该算法更优,在泥石流危险性评估中具有较强竞争优势,有效提高分类效果。

图6 不同模型结果的混淆矩阵对比图Fig.6 Comparison of confusion matrix of the prediction results by different methods

图7 不同模型ROC曲线对比Fig.7 Comparison of ROC curves of different models

表3 4种模型AUC均值对比Table 3 Comparison of AUC mean for 4 models
4 结论
以泥石流危害程度为研究对象,建立了基于PCA算法和经过FA算法参数优化的KELM地质灾害评估模型。利用四川省北川县监测点数据进行实验验证,同时,将本文方法与未进行优化改进的KELM模型、多分类支持向量机模型、BP神经网络预测模型的输出结果进行比较,通过对比验证,表明本文选用的FA-KELM模型在泥石流危险性评估方面效果更优。具体结果如下。
(1) 泥石流灾害的成因是复杂的,致灾因子较多,因此利用PCA进行数据变换和降维处理,经过特征选择的数据更适应模型的训练,去除了因子之间的冗余信息,降低了网络运算量,消耗更少运算时间资源,提高模型准确性。
(2) 由于数据是在复杂严峻的外部环境下采集到的,不可避免地存在不符合要求、重复、错误数据等现象,对输出结果会产生影响,因此对数据集进行了预处理,将预处理前后的数据分别作为模型的输入,得到不同的结果,验证了预处理工作是模型训练前的重要环节,经过数据处理后,提高了数据质量,模型的准确率得到了提高。
(3)将FA优化的KELM方法应用于泥石流危险性评估中。选用FA优化算法对KELM中的参数寻优,并通过ROC曲线和对应的AUC均值对模型进行评估效果的评价,相较于其他3种传统算法,FA-KELM算法展现出更好的效果,评估结果与实际情况基本一致,在实际工程中是可行有效的。
(4)地质灾害的成功预报是极其复杂的系统工程,本文研究主要针对泥石流的危险性进行评估,而对于灾害发生强度、范围和时间的预测也是工程中的难题。同时泥石流灾害从孕育到致灾过程受多种因素导致,且受地形地貌、气象水文影响巨大,本文提出的模型提供一定的参考价值,但还需进一步提高与完善,以便更好地运用于其他流域地区的实际工程中。
