基于深度学习的页岩储层总有机碳含量预测方法

毕臣臣

(中石化石油物探技术研究院有限公司， 南京 211103)

中国页岩气具有成藏条件复杂，埋深较深，勘探开发难度较大等特点[1]。由于成藏机制的特殊性，页岩气与常规油气储层预测方法有所不同[2]，其储层预测的主要任务是寻找页岩的有利“甜点”区。总有机碳(total organic carbon，TOC)含量是评价页岩储层“地质甜点”的重要参数，能够表征页岩的生烃能力，且与含气量成正比[3-4]。通常TOC含量越大，页岩生烃能力越强，对应的含气量也越高[5]，所以TOC含量的准确预测在计算页岩储层含气量及“甜点”目标区优选中发挥着不可或缺的作用。TOC含量预测分为测井预测和地震预测两大类，测井预测TOC方法目前包括单因素法、多元回归法、ΔLogR法和神经网络法等多种较为成熟的方法[6-8]，可以分别利用单个或者多个相关性较高的测井参数来进行TOC曲线的预测，获得单井垂向上的TOC含量分布[9-10]。但仅利用测井的TOC数据难以满足实际生产需求，因此，TOC含量的地震预测成为目前页岩气勘探中研究的热点问题。

目前直接从三维地震勘探资料获取TOC含量的方法较少，地震预测TOC最常用的方法是利用实际测井TOC曲线和与其相关性较高的其他曲线(如密度曲线)进行回归拟合，得到它们之间的函数关系式，再由叠前地震反演结果直接或间接地计算出TOC含量数据体，进而获得三维横向和纵向的TOC含量分布。陈祖庆[11]综合分析了焦石坝地区多口井资料，建立了该区TOC含量与密度之间的线性表达式，并利用叠前反演密度体预测了TOC数据体；李曙光等[12]、王梦等[13]利用该方法实现了川南某深层页岩田和四川盆地LZ区块的TOC地震预测；檀文慧等[14]结合叠前反演结果计算出孔隙度数据体，进而利用TOC含量和孔隙度之间的二次函数关系，预测了丁山地区的TOC参数。然而这些方法只考虑了某单一因素影响，得到的是参数之间简单的一次或二次函数关系。但由于受多种因素影响，页岩储层的TOC含量可能与多个参数之间存在着较为复杂的非线性关系，这种非线性关系还有待进一步挖掘，TOC地震预测精度也有待进一步提高。

深度学习(或深度神经网络)作为目前解决非线性问题的一种有效方法，逐渐被引用到石油天然气勘探开发行业中[15]。陈娟等[16]采用遗传算法-误差反向传播(genetic algorithm-back propagation, CA-BP)神经网络建立了页岩气多个“甜点”参数与测试产量之间的网络模型，提高了页岩气水平井产能预测效率；丁燕等[17]利用深度信念网络(deep belief network, DBN)深度神经网络对裂缝识别参数进行非线性反演，以分频地震数据作为输入，裂缝识别参数作为输出目标，将获得的最优模型应用到整个研究区实现了潜山碳酸盐岩储层的裂缝预测；王锦涛等[18]提出了利用深度学习方法通过训练测井曲线的已知段，来预测缺失段曲线信息；马陇飞等[19]针对致密储层的测井岩性识别模糊的问题，提出基于深度神经网络模型的方法，利用岩性和测井曲线之间的非线性关系对研究区5种岩性进行识别分类。中外学者利用不同神经网络模型来预测TOC曲线，Ouadfeul等[20]构建了具有多层感知器的神经网络模型来预测美国Barnett页岩气田储层的TOC含量；王惠君等[21]以杭锦旗为目标研究区，选择卷积神经网络预测TOC曲线，结合研究区沉积相得到了TOC的平面展布特征；杨占伟等[22]在主成分分析的基础上，选择贡献率较高的4个主成分参数和TOC曲线分别作为输入、输出变量，采用误差反向传播(back propagation，BP)神经网络和梯度提升决策树(gradient boosting decision tree，GBDT)两种方法提高了川南某工区TOC曲线预测精度。但经过调研发现，目前深度学习方法通常是对于曲线的预测，在TOC含量地震非线性预测领域的研究和应用较少。

因此，针对常规TOC地震预测方法的不足以及预测精度较低等问题，现将深度学习引入TOC含量的地震预测研究中，提出基于深度学习的TOC含量地震预测方法。利用川东南某地区页岩储层实测钻井和地震资料，通过建立基于深度学习的深度前馈神经网络模型及模型最优化来充分挖掘并获取TOC含量与多参数之间的非线性关系，然后通过预测误差分析来验证方法的有效性，将其应用到整个研究区中预测TOC含量数据体，以提高研究区TOC含量的地震预测精度，从而更精确地识别页岩气“甜点”有利区，同时为四川盆地页岩TOC含量的地震预测提供一种新的技术方法。

1 方法原理

1.1 深度前馈神经网络模型

深度前馈神经网络是深度学习中比较经典的一种网络结构[23-24]。其特点是除了基本的输入、输出层之外，包含两个及以上的隐含层，每层由多个神经元构成，属于全连接神经网络。隐含层神经元的实质是一个较简单的非线性函数，众多的神经元共同构成了深度前馈神经网络复杂函数。网络中所有信息只朝着一个方向传播，即隐含层神经元对上一层传来的信息进行非线性变换后传递给下一层，经过逐层传送和处理之后，由输出层输出最终结果。前面几个隐含层负责输入数据特征的学习，后面几个隐含层负责对输出数据的预测，从而实现非线性关系的映射。相较于常规回归拟合方法，深度前馈神经网络更适合对复杂的非线性关系进行学习和拟合，可以用来解决页岩TOC含量的预测问题。

训练过程中，每个输入样本数据和神经元输出结果都会随机赋予其每项各自的权重系数w和偏置项b，这个过程遵循每一层输出的方差尽量相等的原则。通过迭代训练得到最优的权重系数w和偏置项b，使得网络的预测TOC结果与实测TOC结果的误差最小，获得最优的TOC含量预测模型。

1.1.1 4层神经网络

以包含2个隐含层的4层深度前馈神经网络为例，如图1所示。其输入数据x1、x2分别为纵波速度、密度，输出数据y为TOC含量，通过设置权重系数w和偏置项b进行参数的初始化。

图1中每个神经元的激活函数为非线性Sigmoid逻辑函数，如式(1)所示，以此可以建立输入、输出参数之间的非线性网络模型。

(1)

式(1)中：z为传递到当前神经元的加权求和结果。

图1 深度前馈神经网络结构示意图Fig.1 Structure diagram of deep feedforward neural network

网络向前传播时，将x1、x2经过加权求和传递给第一隐含层的3个神经元n1、n2和n3，分别得到z1、z2和z3，具体过程为

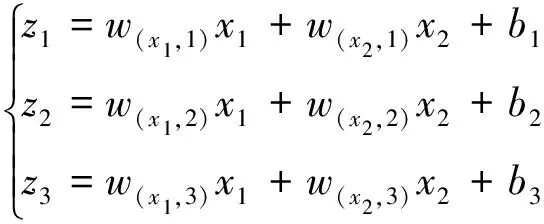
(2)

式(2)中：w(x1，1)、w(x1，2)、w(x1，3)与w(x2，1)、w(x2，2)、w(x2，3)分别为x1、x2传递到第一隐含层3个神经元n1、n2、n3过程中的权重系数；b1、b2、b3为相应的偏置项。

依据式(1)分别将z1、z2和z3输入Sigmoid逻辑函数中进行非线性转换，得到的转换结果为f1(z1)、f2(z2)、f3(z3)。

网络继续向前传播，将f1(z1)、f2(z2)和f3(z3)加权求和结果z4、z5和z6作为逻辑函数的输入，传递给第二隐含层的神经元n4、n5、n6，具体过程为

(3)

式(3)中：w(1，4)、w(1，5)、w(1，6)、w(2，4)、w(2，5)、w(2，6)、w(3，4)、w(3，5)、w(3，6)分别为由第一隐含层的n1、n2、n3，传递到第二隐含层n4、n5、n6过程中的权重系数；b4、b5、b6为相应的偏置项。

同样对z4、z5和z6进行非线性转换后得到第二隐含层的结果f4(z4)、f5(z5)、f6(z6)，并将加权求和结果z7传递给输出层神经元n7，具体过程为

z7=w(4，7)f4(z4)+w(5，7)f5(z5)+w(6，7)f6(z6)+b7

(4)

式(4)中：w(4，7)、w(5，7)、w(6，7)为由第二隐含层的n4、n5、n6传递到输出层n7的权重系数；b7为相应的偏置项。

在输出层非线性转换后，得到最终的预测结果f7(z7)，最终输出结果y即为所预测的TOC含量。

1.1.2 多层神经网络

将上述传播过程推广到L层神经网络。对于第l层网络，根据上一层结果al-1=fl-1(zl-1)、权重矩阵W(l)∈Rml×ml-1和偏置矩阵bl∈Rml，可以得到净输入zl∈Rml。经过ml个神经元激活函数fl(·)的非线性转换，可以得到该层输出al∈Rml，具体过程为

(5)

将整个L层网络看作一个复合函数φ(x;W，b)，将向量x作为第0层的输入a0，将第L层的输出aL作为整个函数的输出，按照式(5)进行信息逐层传递，则整个网络中信息传递过程为

x=a0→z1→a1→z2→…→aL-1→zL→aL

=φ(x;W，b)

(6)

1.2 目标函数求解

Minimizeφ(x;W，b)

(7)

为了获得最优化参数W和b，采用共轭梯度法对式(7)进行求解，使得输出预测值与真实值之间达到最小二乘误差，当达到预先指定的迭代次数时终止优化过程。

1.3 基于深度学习的TOC预测方法

常规回归拟合TOC含量预测方法(回归拟合法)，拟合关系简单，精度较低。利用深度前馈神经网络算法进行TOC含量预测可以同时训练TOC含量与密度、纵波阻抗、横波阻抗等多参数之间的复杂非线性关系，从而提高预测精度。基于深度学习的TOC含量预测方法(深度学习法)流程如下。

(1)训练样本集构建：经过测井资料分析，选择与TOC含量相关度较高的参数作为神经网络模型的输入数据，已知井的TOC含量数据作为输出数据，构建训练样本集。

(2)神经网络构建：设置合适的隐含层数以及神经元数，在保证预测精度的同时，尽量减少计算量。利用前馈神经网络传播算法构建TOC含量预测模型，使得神经网络的信息由输入层逐层、逐单元传播到输出层，计算出整个模型的目标函数值。

(3)神经网络训练：根据实际的样本集，进行神经网络训练，选择合适的迭代次数，以使目标函数值误差趋于最小。

(4)神经网络调优：评估神经网络的性能(即训练拟合精度)，若神经网络性能较好，则将其应用在实际数据上进行TOC含量预测；否则，返回步骤(2)，调整网络结构，重新进行步骤(3)训练，直至误差满足阈值，从而得到最优的TOC含量预测模型。

(5)TOC含量预测：利用所建立的最优神经网络预测模型，对TOC含量数据体进行预测。

2 测井资料网络模型训练与预测

2.1 网络模型训练

研究区川东南某气田共3口钻井，其中Y1井和Y2井具有实测TOC曲线，且分布在研究区南部和北部，因此选择其作为样本数据进行深度学习网络模型构建具有代表性。首先通过对两口钻井的TOC与其他测井曲线进行交汇分析[25-26]，发现TOC含量与密度、纵波阻抗和横波阻抗的相关度较高，呈依次减小趋势，与其他曲线相关度较低。因此，将Y1井和Y2井中与TOC含量相关度较高的密度、纵波阻抗、横波阻抗曲线作为输入样本数据，TOC曲线作为输出样本数据，构建样本集，如图2和图3所示。从样本集中随机抽取20%作为验证集，对网络模型结构进行调试。

首先测试隐含层的个数，将每个隐含层的神经元个数设为定值20，迭代次数设为300，图4显示了隐含层个数为1、3、5、7时的验证误差和训练误差。当网络从0迭代到200次，误差先快速减小后缓慢减小；当迭代次数大于200时误差基本趋于稳定。隐含层数为3时，验证误差和训练误差最小；当隐含层数减少或增加时，误差均有所增大。然后测试隐含层神经元个数，将网络的隐含层个数设为定值3，迭代次数设为300，图5显示了每层神经元个数分别为10、20、30、40时的验证误差和训练误差。当网络从0迭代到200次，误差减小速度先快后慢；当迭代次数大于200时误差基本趋于稳定。神经元个数为20时，验证误差和训练误差达到了最小值。因此，通过上述深度神经网络参数测试，综合考虑预测误差和预测时长等各项因素，最终设置网络参数为3个隐含层，每层20个神经元，利用共轭梯度法对目标函数值最小化，迭代次数200作为本次训练的终止训练条件，此参数下的最小训练误差为0.109 36，最小验证误差为0.104 70。

图2 Y1井实测井曲线Fig.2 Actual logging curve of Y1 well

图3 Y2井实测井曲线Fig.3 Actual logging curve of Y2 well

图4 误差随隐含层数的变化Fig.4 The error varies with the number of hidden layers

图5 误差随隐含层神经元数量的变化Fig.5 The error varies with the number of neurons in the hidden layer

2.2 预测及误差分析

按照上述深度神经网络参数测试结果，进行研究区Y1井、Y2井TOC含量的预测，预测结果如图6所示，图6中蓝色、红色曲线分别为原始和深度学习预测的TOC曲线，二者吻合程度非常高。

为了验证本文方法的优越性，选用常规回归拟合法，进行测试对比分析。图7为Y1井、Y2井回归拟合法TOC预测结果，图7中蓝色、红色曲线分别为原始和预测TOC曲线。对比图6和图7，从两口井的预测结果整体上来看，利用深度学习法预测的TOC曲线与原始曲线基本重合，相关度很高，而回归拟合法预测的TOC曲线与原始值有较大的误差。图8中蓝色、红色曲线分别为深度学习法、回归拟合法两种方法TOC预测结果的绝对误差，图8中可以直观地看出，利用深度学习法预测的误差明显比回归拟合法的误差小。

图6 深度学习法TOC曲线预测结果Fig.6 Prediction results of TOC curve by deep learning method

图7 回归拟合法TOC曲线预测结果Fig.7 Prediction results of TOC curve by regression fitting method

为了定量分析，分别求取了两种方法预测结果相对于实测原始值的相关系数和平均误差值，如表1所示。表1中回归拟合法预测的TOC与实际曲线的相关系数为0.896，平均误差为0.221，而深度学习法预测的TOC与实际曲线的相关系数为0.987，平均误差为0.109。由此可见，相比于回归拟合法，利用深度学习方法预测TOC综合考虑了多种参数与TOC之间的关系，可以同时对两口井的TOC参数特征进行学习，实现了TOC的高精度预测。

图8 TOC预测结果绝对误差对比Fig.8 Comparison of absolute error of TOC prediction results

表1 TOC预测结果相关系数及误差对比Table 1 Correlation coefficient and error comparison of TOC prediction results

3 实际地震资料TOC含量预测应用

为了验证本文方法的可行性和实用性，结合研究区实际地震资料[27-28]，开展TOC预测方法的应用测试。研究区目的层为五峰-龙马溪组页岩，测试之前，已经通过叠前振幅随偏移距变化(amplitude versus offset,AVO)反演获得了可靠的密度、纵波阻抗和横波阻抗弹性参数数据体[29]，如图9所示。前面利用Y1井、Y2井的实际测井曲线，已经建立了针对TOC含量预测的深度神经网络模型。因此，将叠前反演的结果作为输入数据，输入到上述构建好的神经网络模型中，成功预测了研究区TOC数据体，预测结果剖面如图10(a)所示。与常规回归拟合法的TOC含量预测结果[图10(b)]相比，本文深度学习方法横向上分布更为连续，对有利储层的识别更加清晰、准确。与Y1井的录井信息对比分析可以知，预测TOC含量与井上TOC规律一致，龙马溪组整体的TOC含量基本在2%以上，五峰组-龙马溪组底部(图10中过井剖面底部红色部分)表现出较高TOC含量值，其数值可达到6%，说明该处生烃能力好，为含气有利储层。因此，利用深度学习方法来预测TOC含量是可行的，可以提高页岩储层TOC含量的预测精度及分辨率，具有较高的实用性。

图9 叠前AVO弹性参数反演结果Fig.9 Results of prestack AVO elastic parameter inversion

图10 两种方法TOC含量预测结果剖面对比Fig.10 Comparison of TOC content prediction results of two methods

4 结论

(1)TOC含量的预测是页岩“甜点”预测中非常重要的环节。TOC含量预测目前应用较广泛的是回归拟合法，即通过对TOC曲线与密度曲线进行回归拟合，建立线性表达式，再将叠前AVO反演的密度结果代入线性表达式中计算出TOC含量数据体。该方法的拟合关系式简单、考虑因素单一，当研究区有多口井时，或TOC与多个参数均存在较好的相关关系时，无法综合考虑，不能满足实际生产对TOC预测的需求。

(2)基于深度学习的页岩TOC含量地震预测方法，优选出测井上与TOC含量曲线相关度较高的密度、纵波阻抗、横波阻抗曲线作为样本数据，通过调节深度前馈神经网络的模型结构，并利用共轭梯度法进行网络模型参数寻优使目标函数值最小，从而建立TOC含量预测模型。该方法通过建立具有多个隐含层的网络模型，能够充分挖掘纵波阻抗、横波阻抗、密度与TOC含量之间的非线性关系。

(3)实际测井、地震资料的应用结果表明，基于深度学习的页岩TOC含量预测结果与实际资料的吻合程度更高，误差更小。与常规的回归拟合法相比，该方法充分考虑了研究区与TOC含量相关性较高的纵波阻抗、横波阻抗和密度的多因素影响，能够获得多参数之间的非线性关系，提高了页岩储层TOC含量的预测精度及分辨率，具有较高的实用性。