过驱动四旋翼飞行器实验平台姿态跟踪鲁棒控制器的设计与验证
2023-02-24蒲虹宇吴祺煊贺晓华张金鹏
彭 琛, 王 硕, 蒲虹宇, 吴祺煊, 张 鹏, 贺晓华, 张金鹏
(1.电子科技大学 航空航天学院, 成都 611731; 2.江西洪都航空工业集团有限责任公司, 南昌 330096; 3.中国空空导弹研究院, 河南 洛阳 471009; 4.空基信息感知与融合全国重点实验室, 河南 洛阳 471009)
0 引 言
近年来无人机因其具有体型小、 隐蔽性强、 灵活性高、 造价较低等优势, 被广泛应用于各领域中的搜索、 检测、 侦察、 拍摄、 快速锁定目标等工作[1]。 然而, 研究人员在进行实机验证时, 可能会出现种种风险导致运动体的损坏, 从而造成损失。 为了减少这种损失, 仿真实验平台便应运而生。 有机构以四旋翼无人机为蓝本研发了三自由度(3 Degree of Freedom, 3DOF)四旋翼实验平台[2-3]。 四旋翼实验平台保留了实际飞行器的基本特性, 但这些实验平台仍有以下问题: ①过驱动结构带来的控制分配问题; ②实验平台只能通过角位置编码器获取角度测量信息, 而不能获取角速度测量信息; ③实验平台会受到未知不可测的扰动; ④实验平台的电机具有明显的死区及饱和非线性特性。 本文以如图1所示的四旋翼飞行器仿真实验平台为研究对象。 该四旋翼飞行器实验平台的输入是四个旋翼电机的电压, 输出是四旋翼飞行器的三自由度姿态角, 属于典型的过驱动系统。

图1 四旋翼实验平台实物图Fig.1 The quadrotor experimental platform
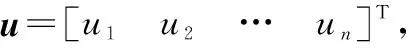

(1)
式中:B为控制矩阵; (ui)min为第i个执行机构操纵量的下限; (ui)max为第i个执行机构操纵量的上限。
伪逆矩阵法是由BODSON提出的经典控制方法[5], 选择的优化指标为操纵量的二次范数, 从Bu=v的无数组解中选取离原点最近的解为最优解[6]。 通过构建的权重矩阵W实现对操纵量进行加权的目的, 增大控制效率较低的执行器的权重值, 可增大执行器输出量, 避免饱和现象在效率较高的执行器中过早出现[4]。
考虑操纵面有约束存在的情况时, 研究人员提出了再分配加权伪逆法[7]。 这种方法具有计算效率高、 实时性好的特点, 但可能会出现结果不收敛的问题[8]。 Hang等[9]提出了一种基于伪逆法的零空间控制分配方法来处理控制输入的约束。 Stephen等[10]基于复用伪逆法的方式改进了级联广义逆法。 Yang等[11]针对航天器的反作用轮提出了一种动态加权伪逆分配方法。 宋佳等[12]设计了一种固定推力器开启数的改进再分配伪逆法的控制分配系统。
此外, 20世纪90年代Durham提出一种直接分配法[13], 通过控制量的最优近似分配控制输入。 Page等[14]提出无约束最小二乘控制分配方法, 通过速度与位置的限制设计代价函数。 Doman等[15]将线性控制分配问题推广到仿射问题。 Harkegard[16]使用二次规划考虑控制分配问题。 针对非线性控制分配方案, 杨恩泉等[17]提出了一种新的多目标非线性规划控制分配方法, 并对非线性控制分配问题的评价指标与方法进行了研究。 闫骁绢[18]提到了一种分段线性规划法, 该方法中首先要对代价函数进行分段线性逼近, 将其转化为混合整数线性规划问题进行求解得到最优控制分配结果。 Naderi等[19]将其控制分配问题转变为规划问题, 并采用矩阵形式变换将非线性的可行域进行简化, 最终得到最优控制分配结果。
在实际应用场景中, 带动桨叶转动的电机存在死区饱和等非线性特性, 正是由于这些非线性特性的存在, 才使得控制律在实际中的控制效果达不到预期。
目前针对电机存在死区饱和特性时的控制问题有很多处理方案, 一种方案是可以将死区饱和非线性问题视为容错控制问题, 进行容错控制分配律的设计: 文献[20]针对执行器存在死区和齿隙非线性的场景, 提出一种基于神经网络算法模型的自适应滑模容错控制器, 实现了执行器存在非线性条件下多操纵面飞机的容错控制; 文献[21]考虑执行器饱和特性, 将其与模型不确定性一起看作是执行器故障的一种, 设计一个由固定控制分配动作以及自适应控制动作组成的控制分配方案, 来补偿执行器故障带来的控制性能偏差; 文献[22]将死区以及效率下降看作是执行器故障, 结合容错控制设计得到一种非并联分布式补偿形式控制器补偿执行器故障带来的控制效能损失。
另外一种方案是结合自适应控制对执行器非线性问题进行自适应补偿; 文献[23]针对具有执行器饱和的不确定过驱动系统, 采用一种元素非对称投影算法约束自适应参数的自适应控制, 弥补了执行器非线性带来的影响; 文献[24]针对具有执行器饱和的过驱动系统, 提出一种自适应控制分配方法, 该方法不需要进行故障估计, 可以在不使用控制输入矩阵估计的情况下容忍执行器的有效性损失, 因此不需要通过持续激励或附加传感器来确定执行器的有效性; 文献[25]主要研究了在存在流体动力学不确定性、 推进器死区和饱和情况下的水下航行器的自适应深度跟踪控制问题, 其中结合梯度投影算法提出自适应有界深度控制律, 达到抑制推进器固有饱和特性的目的; 文献[26]设计了自适应有限时间控制器, 解决了具有全状态约束和死区的严格反馈非线性连续时间系统的跟踪控制问题; 文献[27]通过构造输入饱和参数相关的泛函, 设计得到自适应的增益调度控制器, 保证输入在饱和约束范围内。
通过总结可发现, 上述文献中的过驱动系统都不涉及角度信息不可测的问题, 并且未把执行机构的非线性特性与系统所受到扰动进行同时考虑。 因此在本文中, 针对如图1所示的过驱动四旋翼实验平台, 采用自适应扩张状态观测器(Adaptive Extend State Observer, AESO)对不可测的角速度信息以及扰动信息进行估计, 基于AESO以及PID(Proportional-Integral-Derivative)设计控制律, 之后再采用辅助系统对电机死区饱和非线性特性进行补偿, 并通过伪逆矩阵分配法对系统进行控制分配, 最终实现四旋翼实验平台在无角速度测量信息、 未知扰动影响、 电机存在死区饱和非线性条件下的角度跟踪控制, 并通过仿真以及实验结果验证控制律的有效性。
1 问题描述
根据图1, 定义四旋翼实验平台的1号螺旋桨电机位置为头部, 4号螺旋桨电机位置为尾部, 2、 3号电机分别为实验平台的左侧和右侧。
如图2所示, 针对四旋翼实验平台, 可将地面坐标系定义为Γi={O;i,j,k}, 其中,i、j两轴的正向分别表示正北以及正东方向,k轴正向表示与重力加速度相反的方向。 此外, 定义四旋翼实验平台的机体坐标系为Γb={G;ib,jb,kb},ib指向机头方向,kb表示垂直于机身向上的方向,jb表示满足右手螺旋定则且与轴成垂直夹角指向实验平台左侧的方向。
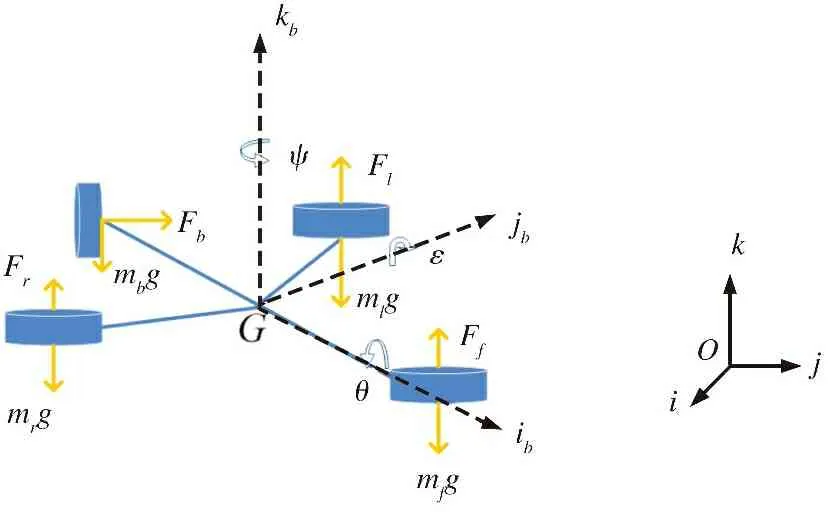
图2 四旋翼实验平台模型原理图Fig.2 Schematic diagram of the quadrotor experimental platform model
四旋翼飞行器的三自由度姿态运动为:
(1) 俯仰(pitch)运动: 螺旋桨电机1、 2、 3通过桨叶的旋转获得升力, 当升力不平衡时, 螺旋桨电机1会绕着万向节进行上下的摆动, 称这种运动为俯仰运动, 俯仰运动的幅度定义为俯仰角(pitch angle), 使用符号ε表示。
(2) 滚转(roll)运动: 当螺旋桨电机2、 3产生的升力不同时, 四旋翼飞行器会以螺旋桨电机1、 4所在的连接杆为轴, 进行上下的摆动, 将这种运动称为滚转运动, 滚转运动的幅度定义为滚转角(roll angle), 使用符号θ表示。
(3) 偏航(yaw)运动: 称四旋翼飞行器绕万向节所在的垂直轴进行的左右摆动为偏航运动, 摆动幅度为偏航角(yaw angle), 使用符号ψ表示。
根据图2构建四旋翼实验平台的动力学模型如下:
(2)
式(2)中所有符号表示意义见表1。

表1 四旋翼实验平台相关符号Table 1 Symbols of quadrotor experimental platform
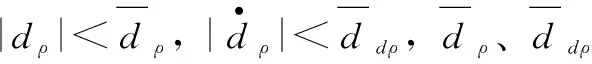
定义转动惯量矩阵J∈R3×3为
定义控制矩阵B∈R3×4为
式中:a1=Lcosθ,a2=Lcosε,a3=Lsinθ·cosε,a4=Lcosθ·cosε。
定义重力矩阵G∈R3×1为
定义系统的控制输入变量U∈R4×1为
定义外部扰动D∈R3×1为
将系统的三轴姿态角向量ρ∈R3×1定义为
则可将式(2)可以改写为
(3)
变换可得
(4)
令
uρ=J-1BU+J-1G
dρ=J-1D
(5)
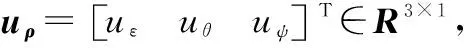
(6)
通过以上步骤, 建立了四旋翼实验平台的数学模型, 并将其转化为如式(6)所示的线性受扰双积分系统形式。 令ρd=[εd,θd,ψd]T∈R3×1表示三轴姿态角期望值, 则本文的目的是设计控制律使得三轴姿态角的实际值能对期望值进行跟踪, 即当t→∞时, 有ρ→ρd。
2 基于AESO方法的实验平台控制
目前, 针对系统中某些状态信息以及扰动信息的估计问题, 常采用的一种解决方法是利用扩张状态观测器(Extend State Observer, ESO)。 ESO在高增益参数下虽然稳态误差小, 但瞬态超调显著变大; 在小增益参数下虽然瞬态超调较小, 但相应的稳态误差变大。 因此本小节在不考虑输入非线性补偿情况下, 采用AESO进行控制律设计, 并对其进行稳定性分析。 下节中将进一步考虑输入非线性补偿情况下的控制律设计。
整体的控制结构如图3所示。 控制律由AESO输出得到的角速度估计信息和扰动估计信息、 期望姿态角信号、 实际姿态角信号构建得到; 之后控制律输入到控制分配环节; 最后将分配的各旋翼电压输入到四旋翼实验模型中驱动其运动并得到实际姿态角信号。 此外, AESO模块中输入实际姿态角信息以及设计的控制律, 得到角速度以及扰动信息的估计值。
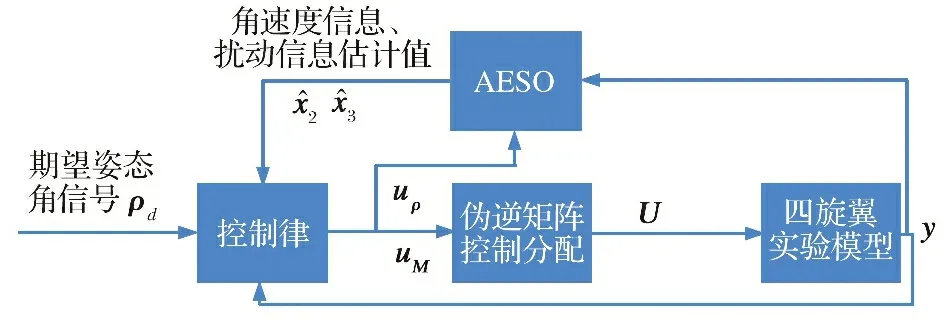
图3 无输入补偿下的控制律设计Fig.3 Control law design without input compensation
图中,U∈R4×1表示四旋翼实验平台各个旋翼电机被分配的升力,uM=BU∈R3×1表示进行控制分配的控制指令,uM通过伪逆矩阵法可得到控制分配后的升力U:
(7)
2.1 基于AESO控制律设计
首先将式(6)中所提到的线性双积分系统改写如下:
(8)
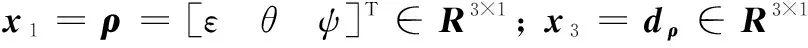
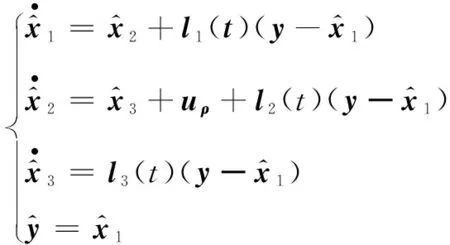
(9)
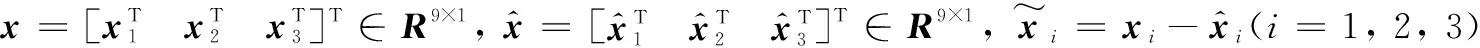
定义:
式中:03×3表示维数为3×3的零矩阵;I3表示维数为3×3的单位矩阵, diag(…)代表将括号中的向量按顺序以分块对角的形式罗列起来形成一个高维矩阵, 并且通过diag(…)得到的矩阵不一定是对角矩阵。 根据上述定义可将式(9)改写为如下形式
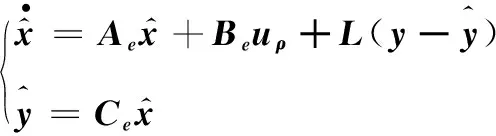
(10)
借鉴文献[29], 设计自适应AESO的时变增益:
(1)令ρ1=-ω0,ρ2=(-0.5+0.866j)ω0,ρ3=(-0.5-0.866j)ω0, 其中ω0∈R3×3是一个对角矩阵, 对角线元素表示3个姿态通道的AESO最大带宽。
(2)定义:
式中:ka为一个小于1的正数;Tω为设计的变化时间。
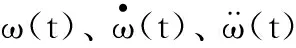
式中:ξi(i=1,2)为巴特沃斯滤波器的设计参数, 则AESO的带宽可以表示为ωn(t)=ω0ω(t)∈R3×3。
(3)取中间变量ai∈R3×3(i=1, 2, 3)为
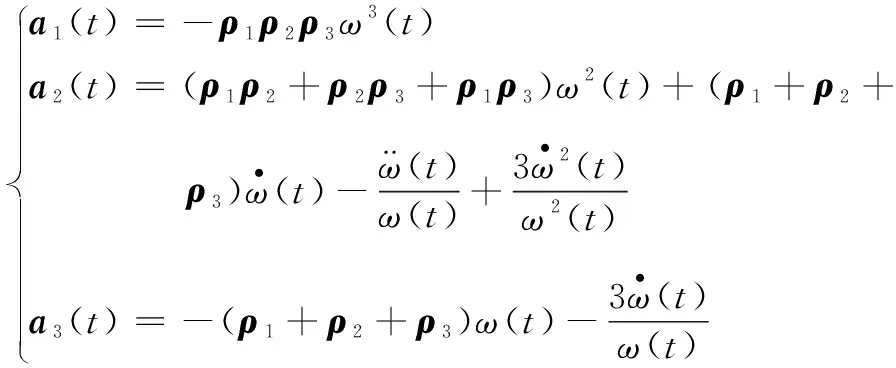
(11)
(4)时变增益可设计为
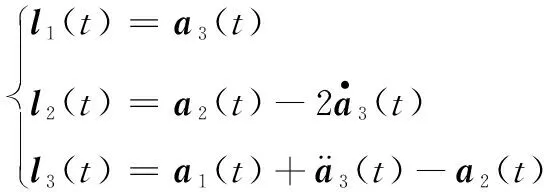
(12)
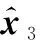
(13)
标称控制律u0采用PID控制进行设计:
(14)
式中:eρ=(y-ρd)∈R3×1表示实际角度值与期望值之间的误差;Kp、KD、KI∈R3×3均为对角矩阵, 对角元素表示PID控制参数。 则控制律uρ可表示为
将式(15)代入式(5), 再结合式(7)中的伪逆矩阵法进行控制分配, 可以反解得到实际输入到模型中的升力为
U=BT(BBT)-1(Auρ-G)
(16)
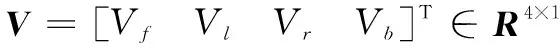
2.2 稳定性分析
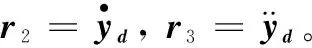
(17)
则可根据式(7)及式(17)推导得到
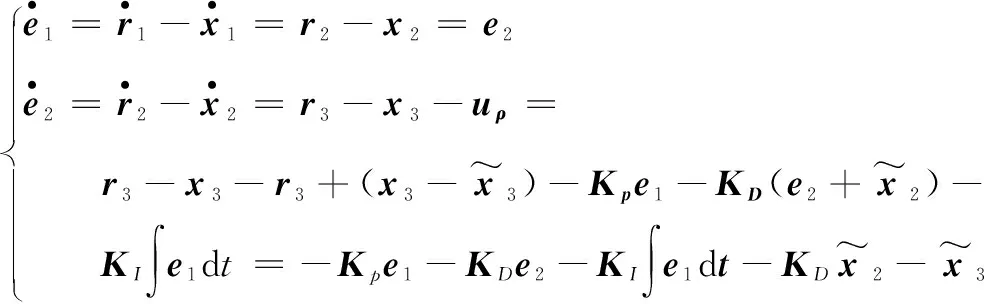
(18)
令
则可将式(18)改写为如下形式
(19)
根据文献[28]中的引理1可得到如下结论:
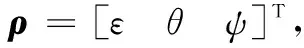
则有:
1) 跟踪误差e对∀t>t0是有界的;
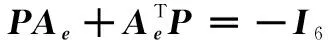
(20)

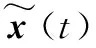
则可证明结论2)。
注释1根据文献[29]可知,ci(i=1,2,…,5)值的大小与AESO的带宽大小ωn(t), 以及观测器增益设置参数l1(t),l2(t),l3(t)有关。 选择合适的观测器增益, 可以影响AESO估计值的精度, 进而影响跟踪误差界值大小, 最终影响基于AESO设计的控制律的控制效果。
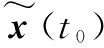
3 输入非线性下的实验平台控制
在实际的机械结构中, 电机对输入电压的响应很少具有标准的线性关系, 电机的输入非线性主要包括三种: 齿隙非线性、 死区非线性、 饱和非线性, 这些非线性因素导致设计控制律的控制效果大打折扣。 由于齿隙非线性带来的控制效果削弱非常小, 因此在本节中主要讨论在电机死区及饱和影响下, 如何对其进行控制律的设计。
本节中采用辅助系统对死区饱和带来的控制效能损失进行补偿, 具体的控制结构如图4所示。 其中, 经过控制分配后得到的控制输入电压先经过死区饱和环节对其大小进行限制, 再输入到四旋翼实验模型中。 经过死区饱和环节前后的电压转变为控制指令uM、UMc输入到辅助系统中, 得到补偿控制律ΔU, 其作用就是抵消电机死区饱和现象带来的控制削弱。 ΔU与期望姿态角信号以及AESO的输出共同构成新的抗电机死区饱和非线性的控制律。
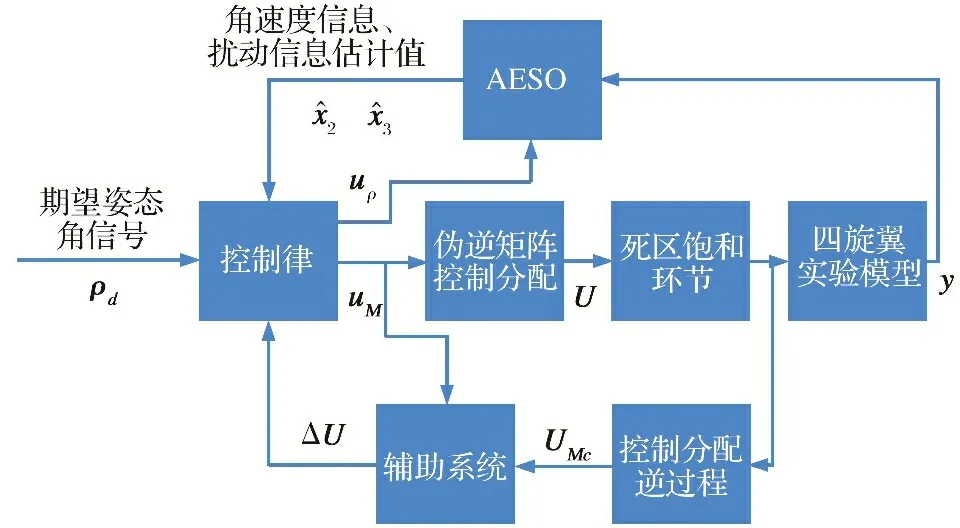
图4 输入非线性补偿下的控制结构图Fig.4 Control structure diagram under input nonlinear compensation
3.1 死区饱和非线性测定
针对四旋翼实验平台, 电机存在死区及饱和等非线性现象, 将对控制器的控制效果产生不利的影响。 在小电压下, 电机由于摩擦力等影响导致电机并不能正常启动, 将电机无转动响应时对应的输入电压区间称为电机死区。 当电压超过某个值后, 电机的转速不再随电压的增加而增加的现象称为饱和现象。 在进行控制器设计前需要对四旋翼实验平台电机的死区饱和范围进行测定。
通过实验测定, 得到的螺旋桨电机输入电压与输出升力之间的关系如图5所示。 点划线为根据原始测量数据拟合得到的电压拉力曲线, 黑色实线为根据点划线得到的标准死区饱和电压拉力曲线。 根据图5中黑色线可以判定-2~+3 V的电压区间为电机死区, -10 V以下以及10 V以上的电压区间为电机的饱和区。 以上分析结果表明, 该实验台是作动器具有明显的非线性特性的过驱动系统, 因此对其设计姿态控制器时, 需要对作动器死区以及饱和特性进行补偿。

图5 电压拉力模型Fig.5 Voltage pull model
结合以上作动器死区以及饱和的特性分析, 可以得到死区饱和函数表达式:
(21)
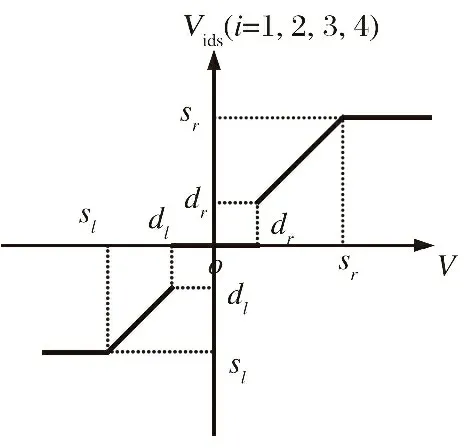
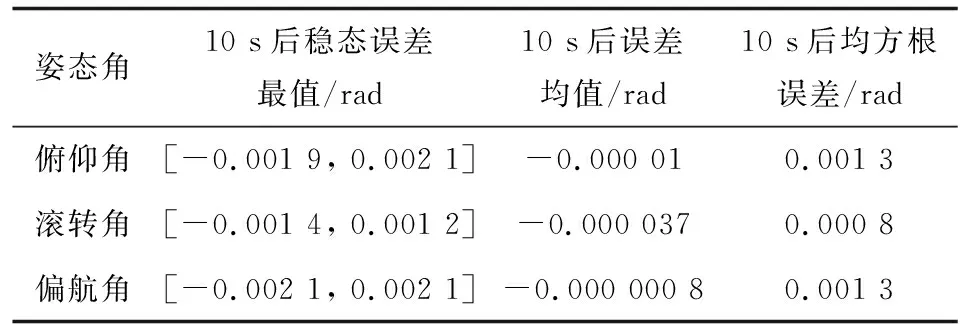
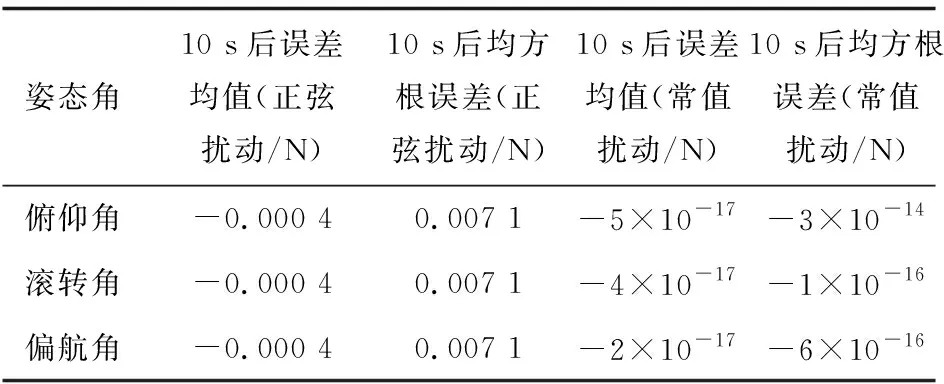
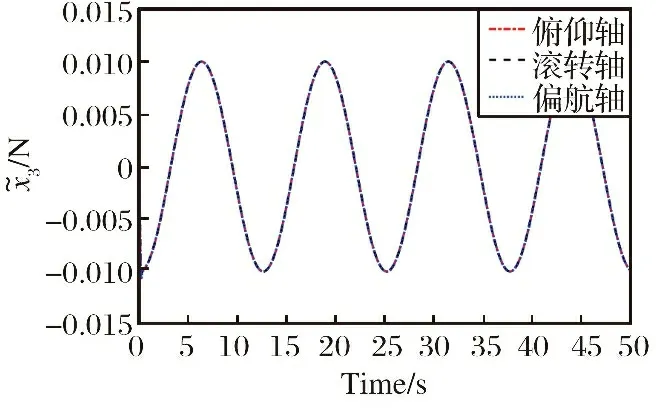
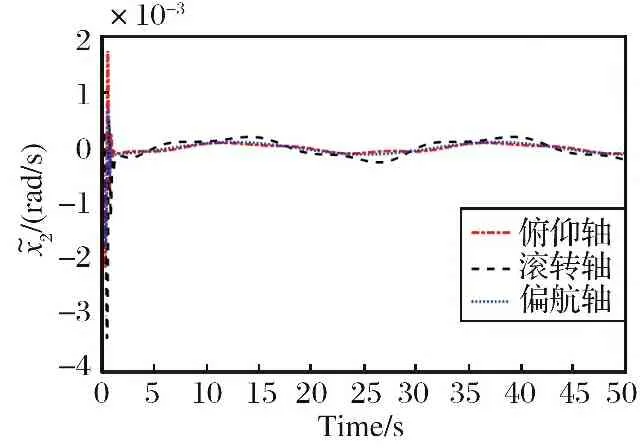
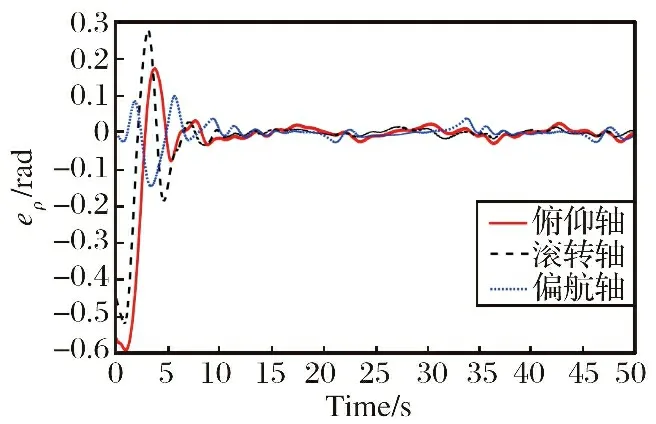
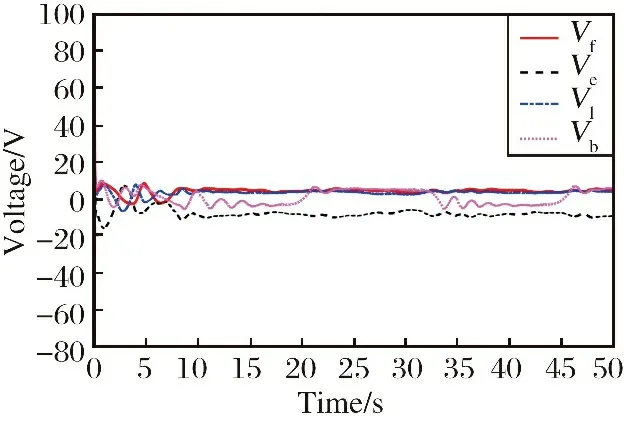
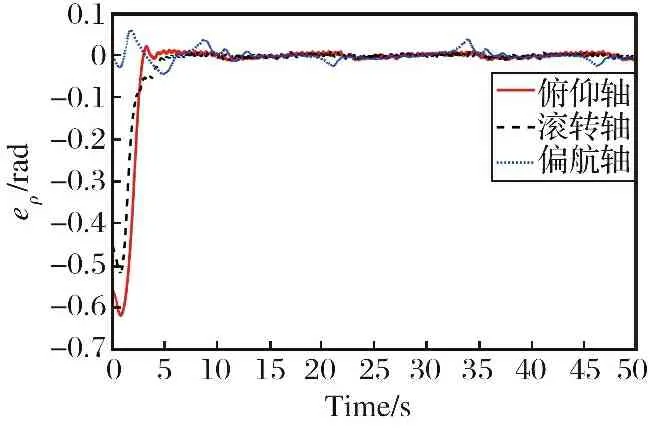
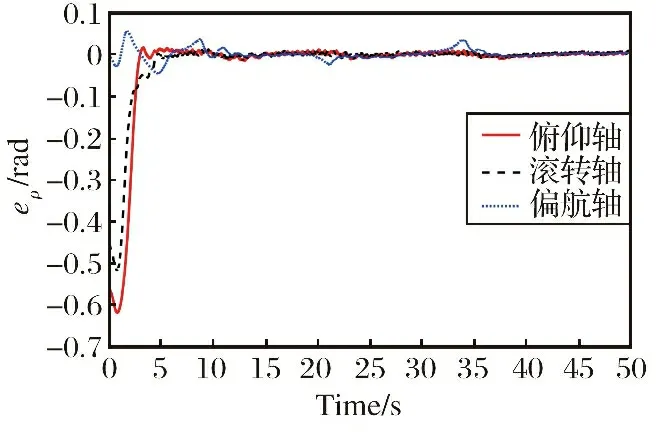
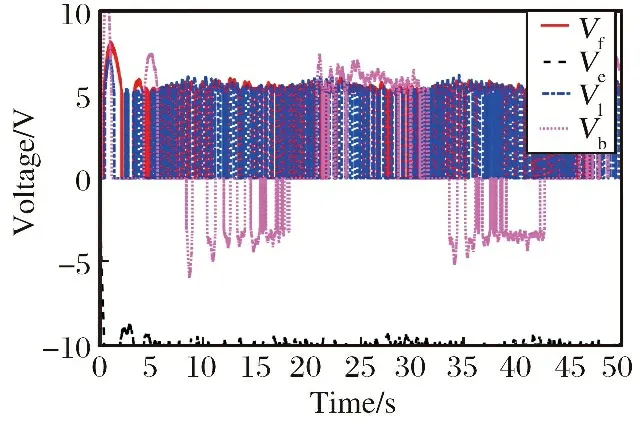
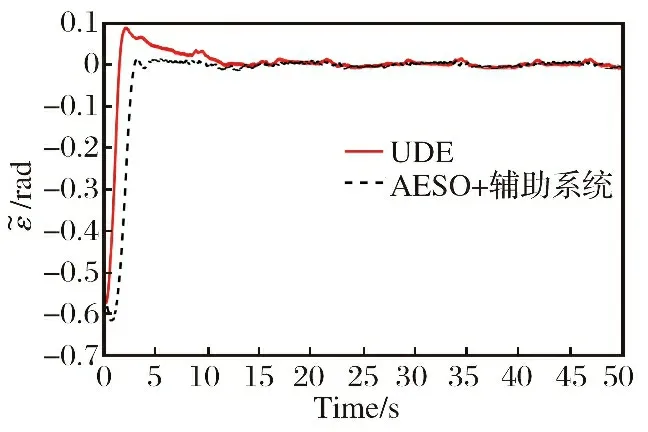
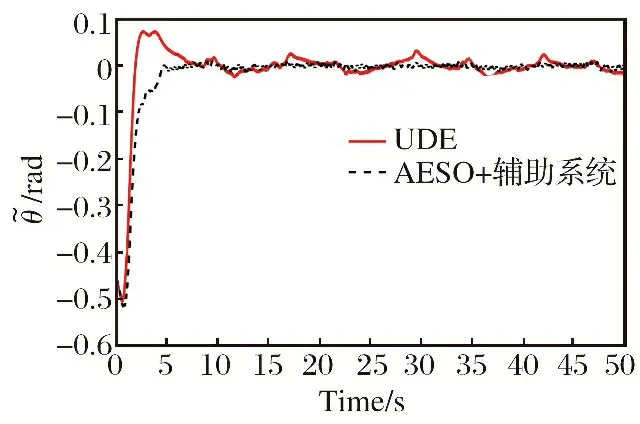
式中: 当v>dr时,kf=kr; 当v 图6 死区饱和环节的输入输出电压对应图Fig.6 Correspondence diagram of input and output voltage in dead zone saturation link 对死区饱和环节的说明: ①其主要作用就是对控制分配后的电压进行死区饱和的限制, 具体表现为: 当控制分配电压在死区区间时, 输出电压大小为0, 当电压在饱和范围内时, 输出电压就是饱和范围的边界值。 ②该死区饱和环节本质上可以看作是对电机本身固有死区饱和非线性特性的数学建模。 无该环节时, 控制分配的电压直接输入到电机中, 此时电压需要经过电机本身固有的死区饱和范围, 才能进行响应。 若输入电机的电压常在死区区间或者饱和区间内, 电机的寿命会变短, 而且会对电机的物理特性产生改变。 增加死区饱和环节时, 对控制分配后的电压进行死区饱和范围对应, 使得输入电机的电压不再经过电机本身具有的死区饱和范围, 使得输入电机的电压一直在图5的线性响应范围内。 ③根据电机本身固有死区饱和数学模型, 由控制指令uM得到的电压V经过电机死区饱和后的实际电压为Vds,Vds经过式(7)所示控制分配的逆过程得到UMc, 利用UMc与控制指令uM之间的差值计算需要补偿的控制律大小。 将辅助系统设计为 (22) 式中: ΔM=uM-UMc;ζ∈R3×1为中间变量;c∈R3×3为需要设计的参数。 将ΔM转变为需要补偿的控制律ΔU: ΔU=Kζ (23) 式中:K∈R3×3为一个对角矩阵, 对角元素是待设计的补偿控制律增益参数。 结合2.1小节中所设计的控制律uρ, 设计考虑输入非线性补偿下的控制律为 (24) 需要说明的是, 式(24)中基于AESO设计并使用的控制律uρ与式(15)形式一致, 而uM未参与AESO的作用过程, 因此uρ与基于AESO所设计控制律的稳定性紧密相关, 结合定理1可知该系统下跟踪误差是有界的。 进行该仿真的目的为: ①验证基于AESO控制律能否在角速度测量信息未知、 存在扰动条件下实现对期望姿态角的跟踪; ②验证AESO对角速度信息以及扰动估计的准确性。 将期望姿态角(单位: rad)设置为 PID的参数取: KI=03×3 AESO的最大带宽参数ω0=30, 对四旋翼实验平台仿真模型的三轴施加时变扰动信息(单位: N)为 仿真结果如图7~9以及表3~5所示。 表3 时变扰动下三轴角度跟踪误差统计数据表Table 3 Statistical data table of three-axis angle tracking error under time-varying disturbance 图7 时变扰动下, 三轴角度跟踪误差Fig.7 Under time-varying disturbance, three-axis angular tracking error 图7以及表3中的结果显示, 仿真中三轴实际角度的跟踪误差均在[-0.002 1, 0.002 1]rad范围内, 三轴角度的均方根误差也非常小, 说明基于AESO设计得到的控制律是有效的。 图8以及表4中的结果显示, 时变扰动仿真条件下, 三轴扰动的估计值与实际值的大小基本一致, 10 s后三轴扰动的估计误差均为-0.000 4 N; 在常值扰动的仿真条件下, 三轴的扰动估计误差在10-17量级, 扰动估计的均方根误差在10-14量级。 说明AESO能够对多种形式的扰动进行准确估计。 此外可以通过增大AESO最大带宽参数ω0的方式缩小扰动的估计误差。 表4 时变扰动下, 扰动估计误差统计数据表Table 4 Statistical data table of disturbance estimation error under time-varying disturbance 图8 时变扰动下, 扰动估计误差Fig.8 Under time-varying disturbances, the disturbance estimation error 图9以及表5中的结果显示, 仿真中三轴角速度的估计值与实际角速度之间的误差均达到10-5数量级, 均方根误差也达到了10-4数量级, 说明角速度估计值可与实际值之间进行精确估计, 说明AESO可对角速度信息进行准确估计。 表5 时变扰动下, 角速度估计误差统计数据表Table 5 Statistical data table of angular velocity estimation error under time-varying disturbance 图9 时变扰动下, 角速度估计误差Fig.9 Under time-varying disturbance, the angular velocity estimation error 进行该实验的目的为: 验证基于AESO控制律相对于基于ESO控制律以及无干扰估计PID控制律的优越性以及AESO的作用。 进行实机实验时, 将期望姿态角(单位: rad)设置为 将式(14)中标称控制器PID的参数设计为 KI=03×3 选取的分段函数为 图10 AESO带宽参数变化曲线Fig.10 AESO bandwidth parameter change curve 得到的实验结果如图11~14以及表6~7所示。 表6 基于AESO设计控制律与无扰动估计控制律下的角度跟踪误差数据统计表Table 6 Angle tracking error data statistics table based on AESO design control law and disturbance-free estimation control law 图11 基于AESO设计控制律下三轴跟踪误差Fig.11 Three-axis tracking error based on AESO design control law 图11中展示了在基于AESO的控制律下, 三轴姿态角跟踪误差曲线, 结合表6中的角度跟踪误差数据可知三轴姿态角的实际值能够跟踪期望值。 故可验证该控制律的有效性。 图12与表7说明在ωn(t)下限值时, 基于ESO设计控制律产生的控制效果时瞬态的超调小, 但后续稳态的误差震荡幅度大, 瞬态的控制效果好。 表7 带宽参数上限与下限时, 基于ESO设计控制律下的角度跟踪误差数据统计表Table 7 Statistical table of angle tracking error data under ESO design control law for the upper and lower limits of bandwidth parameters 图12 带宽参数下限值时, 基于ESO设计控制律下的三轴角度跟踪误差Fig.12 Three-axis angle tracking error based on ESO design control law when the lower limit of the bandwidth parameter 图13与表7说明在ωn(t)上限值时, 基于ESO设计控制律产生的控制效果时瞬态的超调很大, 但后续稳态的误差震荡幅度较小, 稳态的控制效果相对较好。 图13 带宽参数上限值时, 基于ESO设计控制律下的三轴角度跟踪误差Fig.13 Three-axis angle tracking error based on ESO design control law when the upper limit of the bandwidth parameter 将表6~7中的数据进行对比可发现: ①基于AESO设计控制律下的俯仰轴与偏航轴超调, 比ωn(t)上限值时基于ESO设计控制律下的要小; ②基于AESO设计控制律下的三轴稳态误差最值、 均值、 均方根误差值, 均比ωn(t)下限值时基于ESO设计控制律下的要小。 因此可以说明基于AESO设计的控制律结合了两种不同大小带宽参数下基于ESO设计控制律的优点, 对基于ESO设计控制律的控制效果有着明显的改善效果。 图14是无扰动估计控制律下的角度跟踪误差曲线, 结合表6以及图11进行对比, 可以发现相同的控制参数下, 基于AESO设计控制律的控制效果在稳态误差最值、误差均值、 均方根误差值方面均优于无扰动估计控制律的控制效果, 如基于AESO设计控制律得到的俯仰轴稳态误差最值比无扰动估计控制律得到的控制效果要小0.040 6 rad; 基于AESO设计控制律得到的滚转轴均方根误差值是无扰动估计控制律得到的控制效果的1/11倍。 说明了控制律中考虑扰动信息的必要性以及基于AESO设计控制律的优越性。 图14 无扰动估计标称PID控制律下, 三轴姿态角跟踪误差Fig.14 Three-axis attitude angle tracking error under nominal PID control law without disturbance estimator 进行该实验的目的为: ①验证结合辅助系统设计的抗死区饱和控制律的有效性; ②与其他抗死区饱和控制律对比, 验证本文控制律的优越性。 进行实机实验时, 将期望姿态角(单位: rad)设置为 将PID的参数设计为 Kp=diag(30 30 30) KD=diag(30 30 30) KI=03×3 选取的分段函数为 控制效果如图15~23以及表8所示。 表8 各实验条件下三轴角度跟踪误差数据统计表Table 8 Statistical table of three-axis angle tracking error data under various experimental conditions 图15 无死区饱和环节且无辅助系统下, 三轴角度跟踪误差Fig.15 Without dead zone and saturation link and without auxiliary system, the three-axis angle tracking error 图16 无死区饱和环节且无辅助系统下, 控制分配的电压Fig.16 Without dead zone and saturation link and without auxiliary system, the control allocated voltage 文献[3]中将死区饱和非线性看作一种扰动, 基于不确定及干扰估计器 (Uncertainty and Disturbance Estima-tor, UDE)设计了针对四旋翼实验平台的抗死区非线性以及扰动的鲁棒控制律。 作为对比, 分别无死区及饱和环节、 有死区饱和环节但无辅助系统、 基于文献[3]中UDE所设计控制律条件下的实验。 其中UDE的参数为 Kp=diag(30 30 30) KD=diag(30 30 30) TUDE=diag(100 100 100) 图15~16展示的是不施加死区饱和环节下的控制效果, 其主要作为对比实验。 可以看到此时控制分配后的电压在一瞬间出现大尖峰值。 图17~18展示的是只施加死区饱和环节下的控制效果。 其中结合表8将图17与图15进行对比发现: 俯仰轴和滚转轴的超调明显降低、 稳态误差的最值缩小、 均值缩小、 均方根误差缩小, 偏航轴的跟踪效果基本一致,稳态误差均值稍有变大。 结合图18说明实验平台的输入电压全在死区饱和电压范围内时, 可提升控制律的控制效果。 产生这种现象的主要原因是: 施加的死区饱和环节对分配的电压进行了限制, 不会再出现图16中大电压尖峰值的情况, 使得三轴的角度跟踪超调变小。 在偏航轴的控制中, 4号电机比较特殊, 其是垂直于水平面安装的, 使得它在偏航轴的控制中能起到决定性作用, 因此死区饱和环节对偏航轴在稳态时的负面影响较明显, 使得偏航轴稳态误差均值等参数稍有变化。 图18主要展示了死区饱和环节对电压的限制, 可见死区饱和环节可以把控制分配后的电压限制在除0外的非死区区间以及非饱和区间的范围内。 图17 有死区饱和环节但无辅助系统下, 三轴角度跟踪误差Fig.17 With dead zone and saturation link but without auxiliary system, the three-axis angle tracking error 图18 有死区饱和环节但无辅助系统下, 经过死区饱和环节后的电压Fig.18 With dead zone and saturation link but without auxiliary system, the voltage after dead zone and saturation 图19~20展示的是既施加死区饱和环节又施加辅助系统进行补偿下的控制效果。 其中结合表8将图19与图17进行比较, 三轴的稳态误差范围、 均值、 均方根误差值基本一致, 俯仰轴和偏航轴角度跟踪的超调均明显降低, 偏航轴稳态误差的最值减小, 说明偏航轴跟踪的波动幅度降低, 此时图20中显示输入到实验平台中的电压也不在除0外的非死区区间以及非饱和区间的范围内。 以上结果验证了辅助系统抗死区饱和非线性的作用, 同样验证了考虑非线性补偿下设计的控制律的有效性。 图19 有死区饱和环节且有辅助系统时, 三轴角度跟踪误差Fig.19 With dead zone and saturation link and with auxiliary system, the three-axis angle tracking error 图20 有死区饱和环节且有辅助系统时, 经过死区饱和环节后的电压Fig.20 With dead zone and saturation link and with auxiliary system, the voltage after dead zone and saturation 结合图21~23以及表8中的数据, 发现3.2节中所设计控制律得到的控制效果优于基于UDE设计得到的鲁棒控制律下, 俯仰角以及滚转角的超调、 稳态误差等表现, 说明基于UDE设计控制律在对俯仰以及滚转角进行跟踪时, 其瞬态和稳态性能差; 偏航角的误差均值虽小, 但其均方根误差大于本小节中控制律下偏航角控制效果, 说明其稳态误差偏离均值较大; 因此验证了本小节中所设计控制律的优越性。 图21 基于UDE与基于AESO+辅助系统控制律俯仰角跟踪误差对比Fig.21 Comparison of pitch angle tracking error based on UDE and AESO+Auxiliary System control law 图22 基于UDE与基于AESO+辅助系统控制律滚转角跟踪误差对比Fig.22 Comparison of roll angle tracking error based on UDE and AESO+Auxiliary System control law 图23 基于UDE与基于AESO+辅助系统控制律偏航角跟踪误差对比Fig.23 Comparison of yaw angle tracking error based on UDE and AESO+Auxiliary System control law 以上3组仿真以及实验可说明, 本文中基于AESO所设计的控制律相较于基于ESO和UDE所设计的控制律, 具有瞬态超调小、 稳态误差小的特点; 本文中基于AESO以及辅助系统设计的控制律, 削弱了死区饱和非线性特性带来的影响, 提升了控制效果。 本文在存在未知扰动、 无角速度测量信息、 电机存在死区及饱和非线性情况下, 针对四旋翼实验平台的三轴角度跟踪控制问题, 做出以下工作: (1) 利用AESO对未知的扰动以及角速度信息进行估计, 并基于其估计值设计了一种有效的控制器, 保证闭环系统稳定的同时, 改善了闭环系统瞬态响应性能以及稳态性能。 并且对闭环系统进行理论分析, 给出了跟踪误差的最终界。 (2) 基于AESO以及辅助系统提出了一种可对电机死区饱和非线性特性带来影响进行补偿的角度跟踪控制器。 设计并实现多组仿真以及实验, 通过仿真以及实验验证所提控制器的有效性。3.2 输入非线性补偿下的控制律设计
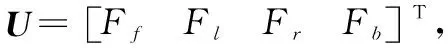

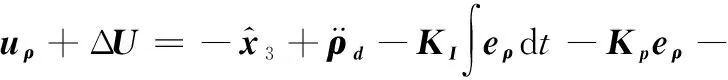

4 仿真以及实验结果
4.1 模拟环境下的仿真


4.2 实机实验一

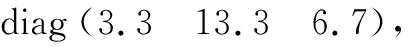
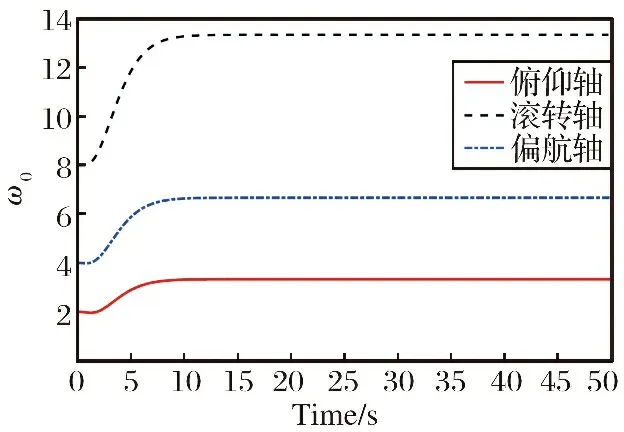



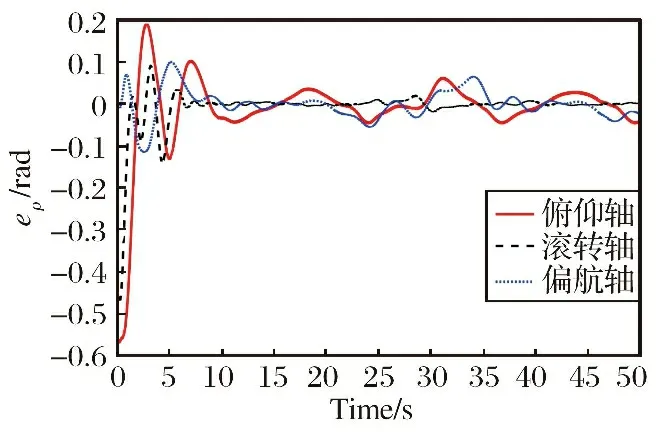


4.3 实机实验二

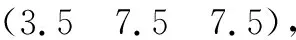



5 结 论
