考虑滑移效应的体外预应力波形钢腹板梁桥的应力增量

杨美良,樊林杰,袁以鑫,刘阳帆

（长沙理工大学 土木工程学院，长沙 410114）

波形钢腹板梁桥是近年来兴起的一种桥梁形式，因其优越的性能而引起广泛关注。最早的法国建成的Cognac桥[1]，有效减小了大跨度桥梁的自重荷载。与传统的PC箱梁桥相比，波形钢腹板箱梁桥结构自重小，能显著降低腹板对上下翼缘板的约束作用，大幅度提高底板的有效预应力，在全球得到普遍推广。

目前，研究者已在波形钢腹板梁桥抗弯[2]、抗剪[3]、疲劳[4]、动力特性[5-6]等方面取得了一定的成果，但对于应力增量的涉及相对较少，且大多数是基于传统的PC箱梁桥，几种比较典型的方法分别是黏结折减系数法[7]、基于截面配筋率指标建立回归公式法[8]、基于变形的计算方法[9-10]和基于能量法[11-12]的计算方法。Antoine等[7]采用黏结折减系数法对预应力混凝土结构进行了研究，得到了考虑剪切变形的应力增量计算公式。Harajli等[13]建立了非线性有限元模型，进行参数拟合，分析体外预应力梁的“二次效应”影响和预应力筋的应力增量。Kim等[14]建立了适用于计算后张法体外预应力连续梁的非线性模型，并将计算出的弯矩分布结果与试验结果进行对比分析，验证了模型的正确性。刘晓刚等[8]采用基于截面配筋指标建立回归公式的方法，进行了无黏结预应力筋应力增量的研究。通过将大量参数进行对比分析，构建了组合结构屈服时应力增量的计算方法。杜进生等[10]开展了关于塑性铰区长度的研究，提出了基于结构变形的应力变化分析方法，并进行了大量的试验梁对比，但并未给出体外预应力筋极限应力的计算公式。刘钊等[11]从能量法的角度入手，推出了结构处在正常使用阶段时预应力筋应力增量的解析解公式。苏俭[12]考虑典型布筋形式与荷载工况，利用能量法推导了体外预应力筋的应力增量解析计算公式，其中考虑了剪切变形的影响。刘玲[15]等进行了6根体外预应力加固混凝土简支梁的试验研究，研究了混凝土强度、跨高比、有效预应力、受拉区普通钢筋的数量等参数对预应力筋应力增量的影响。杜进生等[16]基于理论分析和数值模拟，研究了波形钢腹板组合梁破坏时塑性铰的长度变化，但并没有提出波形钢腹板组合梁体外预应力筋应力增量的计算公式。徐荣桥等[17]基于ABAQUS软件的自定义单元，编写了一个自定义有限元单元，较好地模拟了体外预应力筋的实际情况，能计入滑移效应产生的影响，并基于此构建了应力增量的计算公式，但这是基于传统PC箱梁桥的理论，并不能完全适用于波形钢腹板组合梁桥，后续还需进行针对性的研究。

在现有的体外预应力筋应力增量研究方面，大部分是基于传统PC箱梁桥，针对波形钢腹板组合梁桥建立的应力增量研究鲜有报道。笔者在现有波形钢腹板梁桥试验的基础上，结合Euler-Bernoulli理论，通过预应力筋的变形和结构整体变形的几何关系，推导了考虑滑移效应的体外预应力筋应力增量的计算公式，将公式计算结果与试验梁和Ansys数值模型的结果进行对比，以证明本文理论的适用性。

1 考虑滑移的应力增量模型

考虑一简支梁，结合折线布筋形式，建立简化计算模型，如图1所示，同时对预应力筋做如下假定：

1）在外力作用下，组合梁和体外预应力筋均处于线弹性工作状态，未发生屈曲破坏。

2）未发生剪切滑移时，结构还遵循“拟平截面假定”。

3）考虑钢腹板剪切作用对梁体结构变形产生的影响。

4）忽略预应力筋在锚固端和转向块处的摩擦力，简化受力分析。

设预应力筋端点的初始位置为（xi,yi）(i=1、2、3、4)，形状为三折线。

如图1所示，预应力筋线形简化为三折线形式。为简化计算过程及公式，定义各段为第i段（顶点为i和i+1）（i=1、2、3），则第i段变形前的长度为

图1 计算简图Fig.1 Calculation diagram

如果顶点i的位移用（ui,vi）表示，那么第i段预应力筋发生变形后的总长度可以表示为

展开式（2）并消去高阶小量，化简后可得

其中：θi为第i段预应力筋与x轴之间的夹角，即

根据几何关系，可以得到整根预应力筋在发生变形后的伸长量为

式（5）是通过解得预应力筋在锚固端和转向块处的位移，得到结构整体变形后推导的预应力筋伸长量计算公式。有了伸长量表达式，就能够得到预应力筋在结构变形后的应力、应变增量的表达式分别为

其中：Ls和Es分别表示预应力筋的总长度和弹性模量。根据梁理论，用组合梁的挠度和转角来表示预应力筋在转向块处的位移，可以得到

其中：ei是转向块与中性轴的偏心距（见图1）；Ψ(xi)是梁的转角；ω(xi)是梁的挠度。如果采用Euler-Bernoulli梁理论，那么Ψ(xi)=ω′(xi)。此时，把式（8）代入式（6）、式（7）中，就可以得到Euler-Bernoulli梁理论中预应力筋的应力增量表达式为

因此，得到一个关于挠度的应力增量公式。后续只需求得组合梁的挠度公式，将其代入式（9）中，即可得到预应力筋的应力增量。

2 理论分析

2.1 跨中挠度计算

波形钢腹板组合梁主要的力学特征是：“混凝土顶、底板受弯，钢腹板受剪”。因此，进行挠度的推导时，将同时考虑两种作用的影响：混凝土顶、底板产生的弯曲变形；钢腹板的剪切变形。

在推导两点对称加载情况下（图2）的挠度公式时，一般是先考虑只有一个集中荷载作用时的情况，然后通过叠加原理，得到对称加载时的挠度公式。因此，只需进行集中荷载F下（图3）的挠度公式推导，通过叠加计算，即可求得两点对称加载情况下的挠度公式。

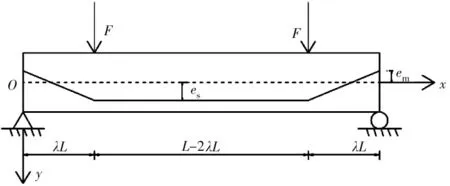
图2 两点对称加载时的计算简图Fig.2 Calculation diagram for two-point symmetrical loading

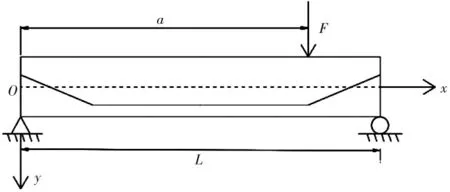
图3 集中力F作用时的计算简图Fig.3 Calculation diagram when the concentrated force F is applied

集中荷载F作用下，组合梁所受的剪力和弯矩表达式可以表示为

式 中：F为 外 荷 载；a为 图2中 集 中 力F与 梁 端 的 距离；L为简支梁跨径。

波形钢腹板的剪切模量采用Johnson等[18]建立的有效剪切模量Ge的计算公式

式中：a、b、α的具体尺寸见图4；Ge为钢板的抗剪弹性模量。

图4 波形钢腹板示意图Fig.4 Sketch of corrugated steel webs

假设只受剪力时，组合梁挠曲线上任一点处的斜率等于该点所在截面的剪应变，那么可得

式中：ω1为简支梁在剪力作用下的挠度；A为竖向抗剪面积，A=2ht，可参见文献[19]，h为钢腹板竖向高度；t为钢腹板板厚；Q(x)为剪力；k为剪切系数，此时取k=0。

将式（11）代入式（13）中，可得到组合梁因发生剪切变形而产生的挠度ω1。

设波形钢腹板组合梁弯矩引起的挠度为ω2，可得

式中：Ec为混凝土板弹性模量；Ic为混凝土板对形心轴的惯性矩。

将式（11）代入式（15）中，可得

根据叠加原理，将式（14）和式（16）按图2所示 进行计算，得到两点对称加载时组合梁的挠度公式

2.2 应力增量求解

得到挠度之后，根据式（9）、式（10）和式（17）可进行应力增量的求解。三折线布筋时，对称荷载作用下

可对应力增量求解公式进行化简

3 数值模型

为了比较验证，依据文献[20]的模型数据和材料设计要求，通过有限元软件Ansys，建立波形钢腹板组合梁全桥数值模型。模拟波形钢腹板组合梁从开始加载到丧失承载能力的受力全过程。

3.1 试验模型数据

以文献[20]的试验参数为基础，简化计算模型，进行预应力筋应力增量的求解。模型梁长4.4 m，宽1.525 m，共设有4道横隔板。体外预应力钢筋为2ϕ15.24钢绞线，抗拉强度标准值fpk=1 860 MPa；顶、底板普通钢筋设计强度为210 MPa，ϕ6 mm的光圆钢筋，横向和纵向间距均为100 mm。具体尺寸和布置形式等见图5。

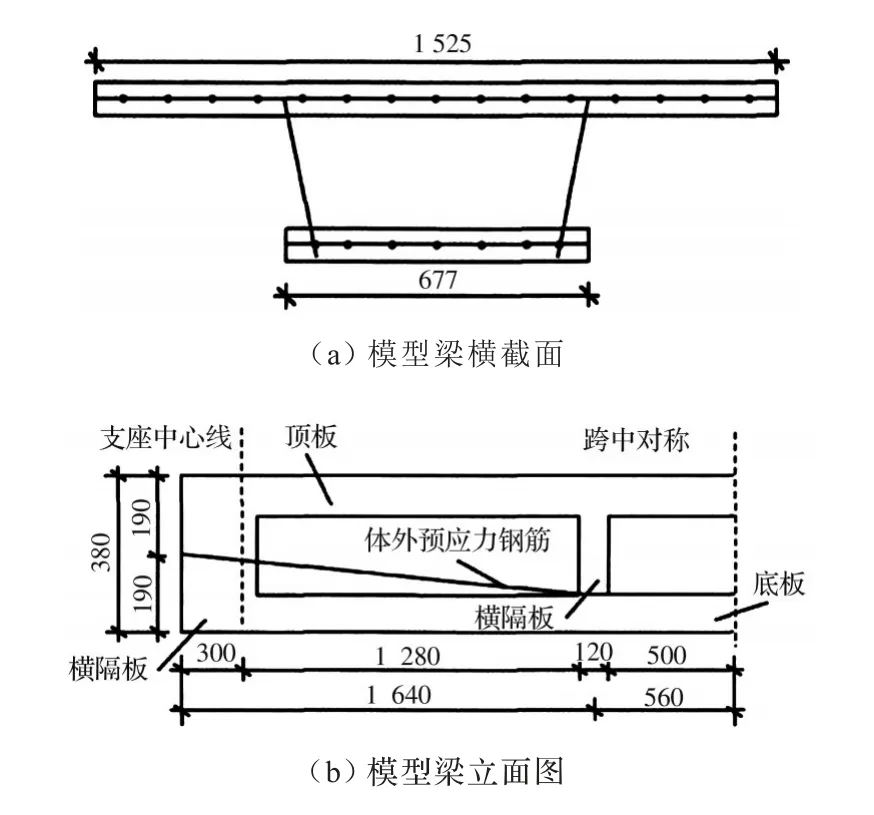
图5 模型截面尺寸（单位：mm）Fig.5 Model section size(Unit:mm)

波形钢腹板厚度为4 mm，细部尺寸见图6，其中：a为直板段宽度；b为斜板段水平宽度；C为斜板段宽度。

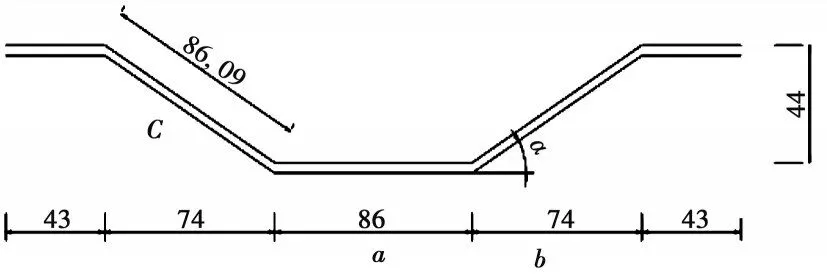
图6 波形钢腹板尺寸（单位：mm）Fig.6 Dimensions of corrugated steel web(Unit:mm)

文献[20]中，模型试验梁加载前需进行挠度、应变和锚下有效预应力测点布置。挠度测点布置在支座和顶板；在顶、底板和波形钢腹板均设置应变测点；试验采用普通钢绞线和智能预应力钢绞线。智能预应力钢绞线内部布置3个光栅测点。同时，在试验梁的张拉端和锚固端均设置锚下有效预应力测点。

体外预应力筋采用单端张拉，张拉力均为120 kN，一次性张拉到位。

试验梁利用反力架做支撑，采用千斤顶进行分级加载，加载方式为两点对称加载。当试验荷载小于110 kN时，采用每级10 kN的荷载增量加载；当荷载达到110 kN时，采用每级5 kN的荷载增量加载，直至梁体塑性破坏。

3.2 材料单元和本构关系

数值模型由混凝土顶底板、顶底板普通钢筋、波形钢腹板、横隔板、支座处钢垫块、加载端分配梁和体外预应力筋几部分组成。

在Ansys众多实体单元中，空间实体8节点单元Solid65是专门为钢筋混凝土材料开发的，可进行非线性处理，具有拉碎和压碎的性能，可模拟钢筋混凝土的开裂、压碎、塑性变形和徐变。因此，混凝土顶、底板选用Solid65实体单元。

波形钢腹板用壳单元Shell93模拟，能考虑剪切变形带来的影响。横隔板采用Solid45单元，同时，为了避免应力集中，在锚固端和转向块处将弹性模量增加到10倍，相当于使其弹性模量无穷大，达到刚体的效果。普通钢筋选用能同时承受拉应力和压应力的Link8单元。

体外预应力筋选用只能单向受拉或者单向压缩的Link10单元，通过添加初应变的方式实现预应力筋的张拉。同时，采用Combin39单元来模拟体外预应力筋在转向块位置的滑移效应[21]。

3.3 模型建立和网格划分

建立实体模型时，通过体分割法建立普通钢筋形成分离式模型，模型建成后，钢筋与混凝土为共节点，可以共同工作，不需要通过耦合来联系在一起。波形钢腹板与顶、底板之间的连接也通过体分割法，在两者连接处形成共节点。在支座处和加载处用实体单元建立垫块，增大其弹性模量，达到模拟成刚体的效果，消除加载不均衡和不对称等因素对计算结果的影响。支座处钢垫块与底板、分配梁与顶板分别施加约束，保证垫块与底板、分配梁与顶板是一个整体。

在进行网格划分时，根据波形钢腹板的形状进行，保持预应力筋、混凝土和波形钢腹板的划分方式相同，保证节点的一致性，能更好地完成布尔运算。

为分析滑移效应对应力增量的影响，共建立两个对比模型。模型一中，预应力筋在转向块和锚固端处用Combin39单元与混凝土粘结，以模拟滑移效应。模型二中，预应力筋在转向块和锚固端处与混凝土进行结点耦合操作，模拟成刚体，没有相对滑移。有限元整体模型如图7所示。

图7 有限元模型图Fig.7 Finite element model diagram

3.4 计算结果及分析

求解过程中，通过荷载步和荷载子步的设置，实现加载梁处逐级加载。直到结构压应力或混凝土压应变超出承载范围而发生破坏为止。提取模型运行后的计算结果，得到跨中截面挠度值和预应力筋的应力值，对比分析文献[20]中试验结果和数值计算结果（图8、图9）。

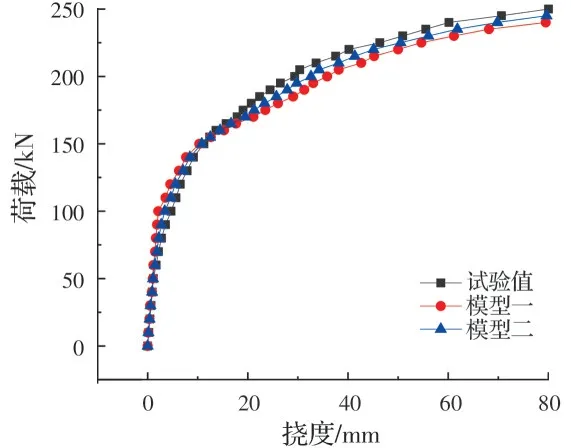
图8 跨中截面荷载-挠度曲线Fig.8 Mid-span section load-deflection curve

图9 有效预应力-荷载曲线Fig.9 Effective prestress-load curve

分析结果表明：模型值与试验值相差不大，验证了模型分析的准确性，较好地拟合了实际情况。从图8、图9中可以看出，曲线有明显的三阶段变化，分别对应模型梁从开始加载到破坏过程中的3个阶段：弹性阶段、开裂阶段和塑性阶段。

弹性阶段：当荷载小于100 kN时，结构处于线弹性受力范围，底板尚未出现裂缝，此时力筋应力变化很小。

开裂阶段：当荷载增大到100 kN时，底板混凝土出现开裂，结构进入开裂阶段，结构刚度明显减小。但由于底板混凝土较薄，受拉区普通钢筋没有屈服，还处于线弹性受力范围，所以结构整体挠度变化很小，应力增量的变化也较小。

塑性阶段：当荷载增大到150 kN后，底板钢筋开始屈服，结构刚度持续降低，进入塑性阶段。结构整体挠度变化和应力增量增长速度显著加快。

当体外预应力筋仍处于弹性受力阶段时，图8所示荷载—挠度曲线大致呈线性增长关系，只有在力筋达到非线性段后，才变为曲线。此时结构整体挠度迅速增大，直至顶板被压碎，模型梁因失去承载能力而破坏。

对比模型一、二的曲线可以发现，考虑滑移效应时，结构整体挠度变形和应力增量增大，承载能力降低。说明滑移效应对应力增量的影响较为明显，不能忽略，在设计时应考虑其影响。

对比荷载—挠度曲线和有效预应力—荷载曲线可以发现，Ansys建模得到的结果和试验所得结果虽有误差，但吻合情况良好，相差不大。说明Ansys模型较好地模拟了试验梁从开始加载到发生破坏的受力全过程。

4 理论公式验证

对比分析理论计算结果、模型结果和试验测试结果（见表1）。

表1 计算结果、模型结果和试验结果对比Table 1 Comparison of calculation results,model results and test results

分析表1可知：

1）推导公式的计算值与文献[20]的试验值相比，误差不超过5%，处于允许范围。计算值与模型值拟合程度较好，验证了公式的适用性。

2）分析模型一、二可知，考虑预应力筋在转向块处的滑移效应时，得到的应力增量比不考虑时的结果偏大，且更为接近试验值。说明力筋的滑移效应带来的影响不能忽视，后续研究中应考虑此因素。

为进一步验证公式的适用性，参考同样布筋形式和加载形式下的模型梁数据，对文献[22]和文献[23]的数据进行理论的验证计算，并进行对比（见表2）。

表2 计算值和试验值对比分析Table 2 Comparative analysis of calculated value and test value

分析表2可得：与试验值相比，公式的计算值偏低，但处于允许范围，且误差不大。表明公式计算所得的应力增量与实际情况吻合良好。

5 结论

1）在考虑预应力筋在转向块处滑移效应的影响工况下，得出结构变形与力筋伸长量之间的理论关系。并结合Euler-Bernoulli梁理论进行简化，推导出适用于波形钢腹板体外预应力筋的应力增量计算公式，将其应用于已有的试验，对公式进行验证，所得误差较小，证明其有一定的适用性。

2）建立的Ansys模型模拟了试验梁从开始加载到结构破坏的全过程。结果表明，模型计算得到的应力增量与挠度近似正相关。在引入滑移效应的影响后，模型的整体变形和应力增量增大，承载能力降低。

3）有限元计算结果表明，以混凝土板开裂和顶底板受拉区普通钢筋屈服为分界点，组合梁的受弯破坏过程经历了弹性阶段、开裂阶段和破坏阶段。