基于ABAQUS牙轮钻头轮体速比计算机仿真研究*
2023-02-24吴泽兵
吴泽兵,王 刚
(西安石油大学机械工程学院,西安 710065)
0 引言
三牙轮钻头是国内外应用最为普遍的牙轮钻头[1-4],随着钻井深度不断地增加,地层越来越复杂。因此国内外学者进行大量的研究试验,分析不同因素对牙轮钻头的轮体速比影响[5-8]。黄春申[9]为了得出不同类型的三牙轮钻头钻资中砂岩和嘉一灰岩的机械钻速,从而开展了大量的室内物理试验来模拟破岩,并通过数据收集得出了这两种钻头的机械钻速,平均传动比随钻压的变化关系,为钻这两种岩石层的钻头的改进和设计提供了重要的试验数据。张强、张晓东等[10]采用正交实验法,研究不同结构齿圈组成的实验牙轮对轮体速比的影响,结果表明不同的齿圈位置、齿数齿形对牙轮钻头的轮体速比都有影响,其中不同的齿圈组合对轮体速比影响最大,随着内排齿向外排齿靠近,传动比下降。每圈齿数对传动比也有显著影响,其中外齿圈齿数比内齿圈齿数影响大。张强等[11]通过用两种不同结构的钻头研究在不同钻压和转速情况下对传动比的影响,分析得出钻压和转速对牙轮钻头传动比都有影响,其中钻压影响较大。况雨春等[12-14]建立了一种动力学模型用于研究岩石与钻杆和钻头的互作用行为。该模型可以较好模拟钻井参数的动态变化,也可研究钻进过程中钻压、扭矩和转速等变换情况。Saouma和Kleinosky[15]使用有限元软件SICRAP模拟裂纹扩展过程。通过与实验比较,表明了将弹性分析与断裂力学相结合可以模拟岩石的切削过程。练章华与马德坤[16]通过搭建室内钻井试验台,用两种不同结构的牙轮钻头钻资中砂岩和灰岩进行大量试验,结果表明钻头的传动比与钻井速度、岩石性质、齿形及钻井参数有着密切联系,为优化这两种钻头结构提供了重要的试验数据。吴泽兵等[17]在ABAQUS软件建立三牙轮钻头全齿与岩石接触模型,通过进行网格划分、材料属性定义、设置边界条件和载荷等进行破岩仿真分析,仿真得到了完整的井底应力分布和各牙轮的轮体速比与钻压和转速的关系,为优化牙轮结构和研究牙轮的轮体速比提供了更为方便的方法。
本文在CERO软件中建立三牙轮钻头的几何模型,将模型导入ABAQUS有限元分析中忽略钻头壳体建立钻头全齿与岩石相互接触模型,定义好网格、岩石性质、边界条件等,研究钻压和转速对牙轮轮体速比的影响,实验结果表明牙轮的轮体速比随着钻压的增大而增大,最后趋向一致,并得出当转速增加到一定程度时牙轮的轮体速比达到最大。最后为了验证该仿真分析软件的准确性,将其和之前学者所做的现场试验数据进行比较。
1 牙轮全齿与岩石互作用模型
1.1 仿真条件假设
由于三牙轮钻头在钻井过程中,牙齿与岩石相互接触在井底运动形式复杂,所以为了方便仿真结果的计算,缩短仿真时间,对整个仿真过程提出以下假设。
(1)考虑在破岩过程中与岩石接触的牙齿有极小的变形,因此将其考虑为刚体。
(2)由于在破岩过程中,钻头时常出现温度升高现象,所以忽略温度对切削齿的影响。
(3)将岩石视为各项同性材料,忽略较大的岩石间隙对破岩的影响。
(4)忽略使牙轮中心不断上下变换的钻头纵向震动。
1.2 仿真模型的建立
应用CREO3.0软件建立由牙轮、牙掌、喷嘴、丝扣和由若干齿圈牙齿组成的三牙轮钻头几何模型,如图1所示。

图1 三牙轮钻头三维模型
首先在CREO软件中将牙轮钻头与圆柱形的岩石进行装配,并将其导入ABAQUS中,由于在破岩过程中是牙齿与岩石相互接触,为了提高破岩效率,节约仿真时间,因此将三牙轮钻头的模型进行简化,只保留与岩石接触的牙齿部分,如图2所示。

图2 钻头全齿模型
1.3 ABAQUS前处理定义
1.3.1 网格划分
在进行有限元仿真分析中,划分网格单元的大小、数量和类型是影响仿真效率和实验准确性关键因素,所以要在满足实验结果准确性前提下尽量减少仿真时间,所以将岩石划分为与切削齿接触的接触区,剩下的为非接触区,由于接触区域只是很小的一部分,所以可以将其网格划分的更加精细,非接触采用较为稀梳的网格,整体采用C3D8R六面体类型网格将其划分,因为C3D8R网格单元更加稳定,由于牙轮牙齿模型较为复杂,为了节约仿真时间,采用四面体网格进行划分如图3所示。

图3 牙齿—岩石模型网格
1.3.2 约束与边界条件
由于在钻头钻井过程中,岩石下表面和岩石四周不受钻进影响,故采用固定约束,约束其6个自由度,在钻头轴线方向施加集中力或速度的方式模拟井底钻压,施加扭矩或转速提供钻头旋转动力。
1.3.3 材料属性定义
岩石属于一种非线性的各向异性的材料,其力学性质较为复杂。在外部载荷作用下,逐渐吃入岩石,在达到应力极限时岩石发生断裂。因此,选择合适的岩石本构模型是确保破岩仿真实验准确性的关键因素。对于一般各向同性岩石可以用不同的参数准则来构造岩石本构模型。考虑到Druker-Prager参数更适用ABAQUS有限元软件,故用其准则作为岩石动态本构模型[18-20]。其屈服条件可表示为:
式中:L2为第二应力不变量;T1为第一应力不变量;b和K为试验常数;τ1、τ2、τ3分别为第一、第二和第三主应力。
具体砂岩岩石参数:密度2 350 kg/m3,弹性模量13 600 MPa,泊松比0.27,内摩擦角50°。
1.3.4 接触定义
在牙轮钻头破岩过程中,岩石受切削齿作用产生形变,由于牙轮运动形式,牙齿和岩石互作用行为存在侵入岩石,滑动最后与岩石分离,再接触下一个岩石单元完成同样步骤,因此选择面-面的接触方式模拟切削齿和岩石接触破岩过程,摩擦因数采用0.3罚接触。
2 仿真结果分析
2.1 牙轮全齿破岩仿真结果
图4所示为仿真过程中三牙轮全齿与岩石相互作用有限元模型和井底应力分布图,可以直观地显示三牙轮钻头的岩石破碎及应力分布情况。由于牙轮绕着钻头进行公转的同时又绕着自身轴线进行自转,所以当切削齿与岩石接触作用时,牙齿对岩石产生冲击、压碎和滑动作用,且由于牙齿与岩石接触时间极短,所以三牙轮钻头齿坑往往存在较多齿坑。

图4 全齿与岩石破岩仿真模型(左)和井底应力图(右)
2.2 钻压对轮体速比的影响
定义钻头转速为60 r/min,研究其在30 kN、60 kN、90 kN、120 kN四组不同钻压下各牙轮的轮体速比,通过观察图5可知4组不同钻压下牙轮的轮体速比大致都开始于0.5,其中在30 kN下有两个节点的传动比都大于1.6,其他3组不同的钻压下传动比都没有超过1.6节点。但是4组不同的钻压下的传动比在不同时刻几乎都在1~1.5进行上下波动,最后通过图6可知在50 kN钻压下牙轮三的平均轮体速比超过牙轮二的,在90 kN钻压下牙轮一的平均轮体速比超过牙轮二的,但是3个牙轮的整体的平均轮体速比是呈上升趋势的,且最后趋向稳定。


图5 各钻压下轮体速比与时间关系曲线

图6 牙轮平均轮体速比与钻压关系曲线
2.3 转速对轮体速比的影响
定义钻头钻压为60 kN,研究在30 r/min、60 r/min、90 r/min、120 r/min四组转速下各牙轮的轮体速比,通过图7可知在4组不同转速情况下牙轮钻头的轮体速比也大致都开始0.5,在30 r/min牙轮一的传动比发生异常,在短时间内没有进行波动,4组不同转速下牙轮的传动比在不同时刻基本也都在1.0~1.5这个范围内上下波动。并且观察图8可知当达到一定转速时,牙轮的轮体速比达到峰值不再增加。

图7 不同转速下牙轮轮体速比

图8 牙轮平均轮体速比与转速关系曲线
3 验证仿真实验的正确性
练章华[16]通过大量研究试验表明,用某种钻头钻同一种岩石时,在其他钻井参数一样的条件下,牙轮钻头的传动比总是最后趋于统计平均值。张强[11]研究不同的钻井参数(钻压和转速)对牙轮钻头传动比的影响,经分析得出牙轮钻头的传动比在不同钻压和不同转速下都在一定区间内(1~1.5)发生阶跃跳动,并且随着钻压的增大其传动比平稳增加最后趋于某一统计平均值。吴泽兵[17]使用ABAQUS有限元分析软件探究不同钻压对钻头轮体速比的影响,通过进行材料属性定义,网格划分,边界条件设定等一系列设定后分析得出随着钻压的增大牙轮钻头的轮体速比也逐渐增大并趋向某一平均值(图9),因此从前人所做的现场试验结果和仿真结果来看,此次仿真实验的正确性[21-22]。
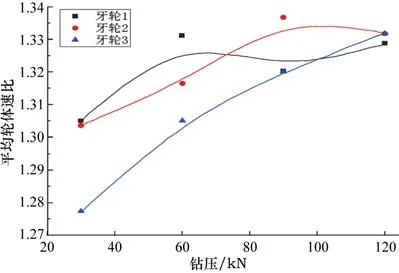
图9 预测结果
4 结束语
(1)使用ABAQUS软件进行了三牙轮钻头全齿破岩仿真分析,得到了较为完整的井底应力分布图,了解到三牙轮钻头轮体速比随时间随机变化,基本保持在1~1.5这个范围内。
(2)通过仿真模拟了钻压对轮体速比的影响,得出随着钻压的增大,各牙轮的轮体速比逐渐增大且趋于稳定。
(3)通过仿真模拟了转速对轮体速比的影响,得出当达到一定转速时,牙轮的轮体速比达到峰值不再增加。
(4)最后将实验结果与前人所做的现场试验数据进行对比来验证使用有限元分析软件研究钻头传动比的可靠性,本文成果为研究牙轮钻头传动比提供了一种有效的仿真试验方法,为设计性能更好的钻头提供了一定的技术手段。
