基于ISOA-RBPNN的埋地管道剩余强度预测*

2023-02-24骆正山彭红发

中国安全生产科学技术 2023年1期

骆正山，彭红发

（西安建筑科技大学管理学院，陕西西安 710055）

0 引言

由于环境、运输介质等原因，油气管道在服役期间易发生腐蚀，导致管壁变薄、强度降低，甚至造成管道泄漏事故，危及人员安全和生态环境。因此，预测油气管道剩余强度对于管道安全运营尤为重要。

目前，油气管道剩余强度计算主要是利用各种评价规范准则和有限元分析。国外提出的相关规范准则大部分是基于特殊实验环境得出，文献[1-5]实质大都为经验或半经验关系式，其准确性较低。有限元分析方法经常应用于油气管道剩余强度领域，郑恒伟等[6]、杨燕华等[7]、马廷霞等[8]、臧雪瑞等[9]和王艺斐等[10]利用ABAQUS 软件建立腐蚀管道的有限元模型。在模拟不同管材及腐蚀类型有限元分析时，必须设置不同失效准则；若研究对象发生变化时，则需重新计算，因此有限元的实时性较差。随着人工智能技术的迅速发展，工程安全管理领域不断出现新理论，其中人工神经网络具有较强的自学能力，不需要通过人为实验法确定实验相关参数，从而避免人为实验误差对参数的影响[11]。徐鲁帅等[12]利用差分进化算法优化BP神经网络，预测含腐蚀缺陷管道失效压力。张新生等[13]、李琴等[14]和贾思奇等[15]运用群体智能算法优化BP神经网络，构建管道失效预测模型。凌晓等[16]针对群体算法易出现局部最优等问题，提出使用改进萤火虫算法，对BP神经网络预测模型中的参数进行优化，预测管道外腐蚀速率。但上述改进方法均为直接采用智能算法优化BP神经网络的初始权值和阈值，且少有文献考虑到预测模型易陷入局部最优的问题。由于BP神经网络存在迭代速度慢的缺陷，直接利用智能算法优化参数也无法达到满意的预测效果。

综上所述，本文提出以弹性梯度下降法改进BP神经网络研究管道剩余强度，与传统BP神经网络相比，迭代速度得到较大提升。通过对海鸥算法进行多方面改进，可有效避免陷入局部最优，构建ISOA-RBPNN腐蚀管道剩余强度预测模型，预测精度更高。本文实验以79组管道爆破数据进行验证分析，与目前研究领域内预测性能较好的2 种改进BP神经网络模型进行统计学指标对比。研究结果可为后续研究腐蚀管道剩余寿命和制定维修策略提供参考依据。

1 理论基础

1.1 BP神经网络

BP神经网络是由Mcculland 和Rumelhart为代表的PDP小组提出的误差反向传播算法[17]。BP神经网络组成结构包括：输入层、隐含层和输出层，如图1所示。神经网络中节点代表神经元，通过对应权值连接前后2 层神经元。BP神经网络通过训练前面1 层网络固定阈值和权值，将其输出作为下1 层网络的输入，完成训练后，再用反向传播算法不断调整阈值和权值，直到误差信号达到输出要求。

图1 BP神经网络结构Fig.1 Structure of BP neural networ k

1.2 海鸥优化算法

海鸥优化算法（seagull optimization algorithm，SOA）是根据海鸥的迁移和攻击行为所提出的1 种新全局搜索算法[18]。SOA模拟海鸥种群在迁徙过程中如何从1个位置转移到另1 个位置，且需满足3 个条件：避免碰撞、向最佳位置移动、保持与最佳海鸥接近。获取最佳位置范围后，海鸥通过螺旋式运动不断更新搜索海鸥与最佳海鸥位置，直到到达最佳位置。

2 改进海鸥优化算法（ISOA）

2.1 Cat混沌映射优化种群初始化

种群初始化对SOA算法的预测精度影响较大，Cat映射可以避免种群分布倾向于聚集某几个位置，在[0，1]内均匀分布，引入Cat混沌映射优化SOA算法的种群初始化，可显著提高算法的寻优能力和迭代速度[19]。假设种群规模为100，SOA算法种群初始化如图2所示，其个体分布较为杂乱；Cat混沌映射优化种群初始化如图3所示，其个体分布均匀。而SOA算法具有更好的遍历性。

图2 随机初始化种群Fig.2 Random initialization population

图3 Cat映射初始化Fig.3 Cat map initialization

2.2 优化搜索方向

在攻击过程中，海鸥会发生螺旋式运动，并以此更新海鸥位置，该过程可用式（1）描述：

式中：r为每次螺旋运动半径，m；k为[0，2π]的随机数；u 和v为“螺旋运动”形状的常数；x′，y′，z′表示螺旋运动的位置。

传统海鸥算法在局部搜索阶段的单向搜索，位置变化方向不可更改，通过引入随机数控制位置变换方向，将单向搜索改进为双向搜索，提高SOA算法的全局搜索能力，其原理如式（2）所示：

式中：Hs（t）为攻击位置；Ds（t）为搜索海鸥所在位置和最佳位置的距离；x，y，k为控制搜索的系数；Hbs（t）为个体最佳位置；R为随机数。

2.3 优化攻击形式

海鸥群落攻击猎物位置进行纵向交叉与横向交叉，提高下次迭代精度。横向交叉类似于遗传算法中的交叉变异，由此产生优于父代的海鸥个体如式（3）所示：

式中：MShc（i，d）和MShc（j，d）为子代，A=X（i，d）和B=X（j，d）为父代的2 个体，父代与子代对比保存优势；惯性权重r1和r2为[-1，1]范围内的随机数，学习因子g1和g2为[0，1]范围内的随机数。

纵向交叉是指粒子在不同维度的交叉，可在不影响其他维度情况下跳出局部最优，归一化之后才能进行纵向交叉，且每更新1 个维度都需要进行纵向交叉，纵向交叉更新维度的原理如式（4）所示：

式中：MSvc（i，d1）为d1维的子代；τ为[0，1]范围内的随机数。

3 构建ISOA-RBPNN模型

传统BPNN常采用误差梯度下降法调整相应的权值和阈值，导致模型迭代速度慢，引入弹性梯度下降法可以有效克服该问题[20]。修正权值和梯度大小无关，仅和梯度符号相关，其原理如式（5）所示：

式中：Δ（t）ij为更新值；为均方误差梯度。

更新后的权值如式（6）所示：

假设原始数据共有N个因素，并对其进行归一化处理，训练集k组，测试集s组，对油气管道剩余强度有影响的因素Z=[Z1，Z2，…，Zm]，则BP神经网络的输入层节点数为n，如式（7）～（9）所示，确定隐含层数量M，通过ISOA寻找RBPNN 的最优权值与阈值，最终构建ISOA-RBPNN模型预测腐蚀管道剩余强度。

式中：k为训练集数量；n 为输入层节点数；m为输出层节点数，m=1；M为隐含层数量；a 为[0，10]的常数。

4 实例验证

4.1 数据来源

为验证预测模型准确性，根据某石油天然气输送管道风险评估项目实测数据，并参考文献[21]多次筛选后选取79 组代表性管道爆破数据，该数据涵盖管道钢级X42～X100 的常见类型。不同管道钢级（Z1）、管径（Z2）、壁厚（Z3）、缺陷深度（Z4）、缺陷长度（Z5）、抗拉强度（Z6）为管道剩余强度主要影响因素，部分数据如表1所示。

表1 管道爆破数据Table 1 Pipeline blasting data

4.2 RBPNN模型参数寻优

由于指标间的单位存在差异，因此对原始数据进行归一化处理。BP神经网络输入层为影响管道剩余强度主要因素，所以输入层设6 个节点，输出层为腐蚀管道剩余强度。由公式（7）～（9）可确定隐含层节点大致范围，通过对比不同节点数输出结果的误差，确定节点数为10，隐含层层数为2。设初始海鸥种群个数为20，最大迭代次数为100，采用均方根误差作为适应度函数，获得SOA和ISOA的适应度对比图，如图4所示。ISOA从第37 次迭代开始适应度值保持在0.009 99，达到收敛状态，而SOA在第59 次迭代才达到收敛状态，适应度值为0.164 31，ISOA更快达到收敛状态，且适应度值更低，证明ISOA收敛速度和预测效果均优于SOA。

图4 适应度对比Fig.4 Fitness comparison

4.3 模型评价指标

为评价不同模型预测效果，选取平均相对百分比误差（MRE）、决定系数（R2）和均方根误差（RMSE）作为模型的性能评价指标，相关表达式如式（10）、式（11）、式（12）所示：

4.4 ISOA-RBPNN模型预测结果对比分析

PSO-BPNN、IFA-BPNN及ISOA-RBPNN模型均为利用智能算法优化BP神经网络，PSO-BPNN和IFA-BPNN模型为目前主流预测方法，且预测效果较好。为验证ISOA-RBPNN模型预测效果更好，与PSOBPNN、IFA-BPNN模型预测结果进行对比。在归一化处理后的79 组爆破数据中随机抽取70 组作为训练集，剩余9 组作为测试集，3 种模型预测结果如表2所示。PSO-BPNN模型预测结果的平均相对误差为9.56%，IFA-BPNN模型预测结果的平均相对误差为5.29%，而ISOA-RBPNN模型预测结果的平均相对误差仅为2.58%，预测精度得到较大提升。且ISOA-RBPNN模型在各检测点的相对误差均小于其他2 个预测模型，证明ISOA-RBPNN在预测腐蚀管道剩余强度方面效果更好。

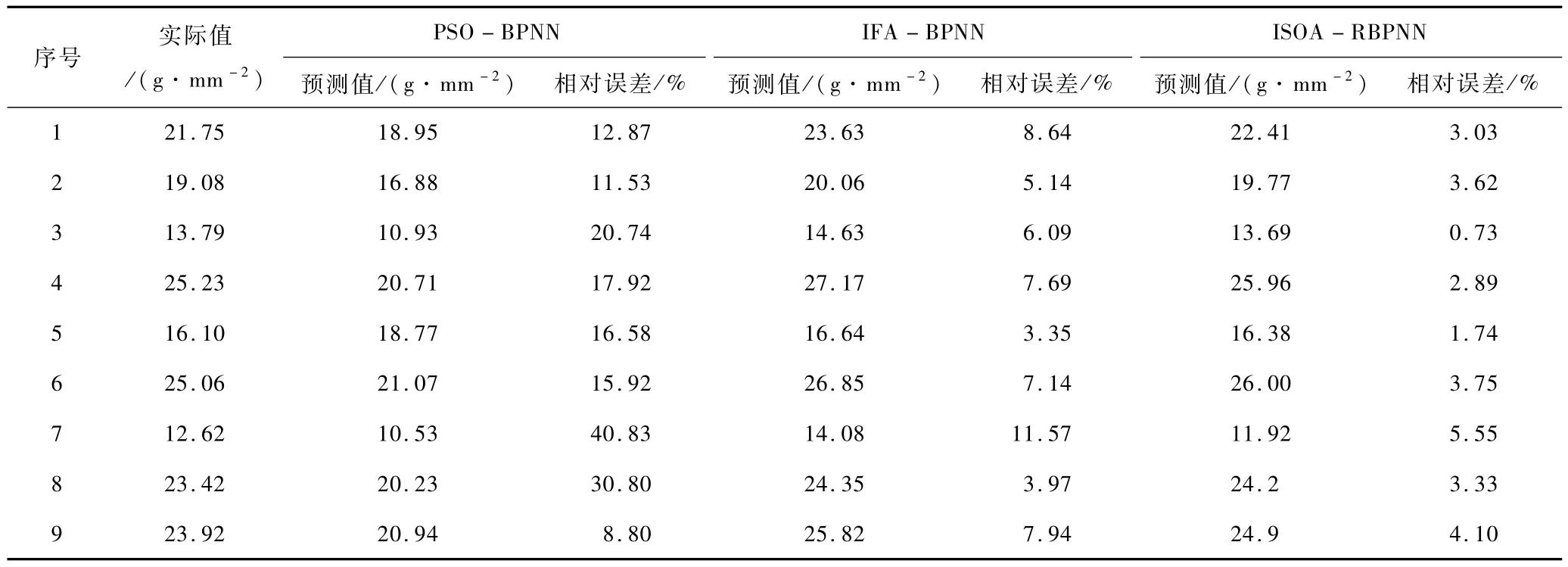
表2 3种模型剩余强度预测对比Table 2 Comparison on residual strength pr ediction of three models

由图5～6 可知，ISOA-RBPNN 模型，与PSOBPNN模型和IFA-BPNN模型对比，预测精度得到较大提高，模型预测值更接近实际值。ISOA-RBPNN模型的平均相对百分比误差为4.29%和均方根误差为0.97 MPa均低于其他预测模型，决定系数为98.89%更接近1，证明ISOA-RBPNN模型对腐蚀管道剩余强度具有更好的预测性能。

图5 模型预测结果对比Fig.5 Comparison of model prediction results

5 结论

1）传统BP神经网络模型收敛速度慢，且易陷入局部最优，引入弹性梯度下降法优化BP神经网络，模型的收敛速度得到较大提升，利用ISOA优化模型参数可有效避免局部最优问题对预测结果的影响，并提高该模型的全局搜索能力和预测精度。

2）使用ISOA对弹性BP神经网络中的权值和阈值进行寻优，本文所构建的ISOA-RBPNN腐蚀管道剩余强度预测模型，保留BP神经网络较强的非线性映射能力和自适应能力，且该模型的各项统计学指标均优于PSO-BPNN和IFA-BPNN模型，其决定系数、平均相对百分比误差和均方根误差分别为98.89%、4.29%和0.97 MPa，表明该模型预测值与实际值基本一致。