海上超高温高压钻井井筒温度压力场耦合研究*
2023-02-24张万栋向世林
张万栋,罗 鸣,吴 江,韩 成,向世林,张 智
(1.中海石油(中国)有限公司湛江分公司,广东 湛江 524057;2.西南石油大学油气藏地质及开发工程国家重点实验室,四川 成都 610500)
0 引言
随着对油气资源需求的持续增长,以及石油和相关学科领域的技术水平大幅提升,油气勘探开发工作正在稳步向高温高压油气井发展,高温高压油气藏已经逐渐成为油气勘探开发的重要区域,超高温高压油气藏也将成为未来勘探开发的重要领域之一[1]。我国南海高温高压领域天然气资源量达15 万亿m3,占南海油气总资源量的1/3,是我国能源重要接替区和国家“一带一路”战略能源保障基地。中国南海与美国墨西哥湾、英国北海并称全球3 大海上高温高压区域,中国南海莺琼盆地已钻井井底温度可达249 ℃,井底压力达142 MPa,储层压力系数高达2.38,属于典型的超高温高压领域[2-3]。
按照油气层温度压力等级,油田服务公司和API标准[4-5]开展高温高压分类标准的划分,中海油超高温高压井划分标准为[6]:井底温度高于177 ℃、压力高于103.45 MPa(15 000 psi)或孔隙压力当量密度大于2.10 g/cm3的井。目标区块地层压力系数在2.30 左右,储层温度在200 ℃左右,属于典型的超高温高压,部分井到达极高温高压,其钻探是公认的世界级难题。与常规油气井相比,由于超高温高压地层窄安全密度窗口问题突出,储层段安全钻井密度窗口可低至0.10 g/cm3及以下,且超高温高压特殊的温度、压力环境对钻井过程中井筒内钻井液的密度和流变性影响明显,对超高温高压井的井筒温度压力预测及控制提出更高要求[7-11]。
国内外学者对井筒瞬态温度压力预测模型开展大量研究,Hasan 等[12]、Ramey[13]、Willihite[14]的经典预测模型并未将温度压力耦合起来进行求解,井筒温度压力预测精度存在一定限制;杨谋等[15]基于钻井全过程各井筒单元传热机理,建立钻井循环与停止循环期间井筒-地层瞬态传热模型;郑友志等[16]考虑定向井井型的影响,建立井筒瞬态温度压力耦合计算模型;Falavand等[17]考虑钻屑及地层瞬态热反应的影响,建立气-液-固三相流的井筒温度压力预测模型。部分学者针对海上超高温高压钻井难点,进行ECD精准预测与控制[18]、控压钻井[19]、作业模式[20]、配套钻井技术[21-22]等分析研究,但并未深入对海上超高温高压钻井井筒温度压力进行耦合预测研究。
因此,本文依据海上超高温高压钻井的特点,基于流体力学和传热学理论,将井筒瞬态传热划分为钻柱段、海底泥线以下环空段、隔水管环空段3 个区域进行分析,并综合考虑超高温高压的井筒环境对钻井液密度、流变参数的影响,建立海上超高温高压钻井井筒温度压力耦合瞬态预测模型;在此基础上,利用实例井现场随钻数据进行模型验证,分析正常钻进期间井筒温度压力的耦合变化规律,评价钻井液的物性参数变化对耦合结果的影响机理,以期降低海上超高温高压地层窄密度窗口中的安全钻进风险,为海上超高温高压钻井井筒温度压力精准预测及控制提供理论支撑。
1 钻井井筒传热物理模型
在钻井液循环过程中,随着井筒内热量不断的交换,井筒内流体的温度将不断变化,而影响整个井筒的压力分布;反过来,井筒的压力分布变化又将进一步影响井筒的温度分布,这是1 个温度压力相互耦合的过程。井筒内传热物理模型如图1所示,图中Δr,Δz为径向和轴向单元距离,m;Tp,j,Ta,j,Tcem,j分别为空间节点j处的钻柱内温度、环空内温度、水泥环温度,℃;Ti,j为井筒传热控制单元i在空间节点j处的温度,℃。

图1 井筒传热物理模型示意Fig.1 Schematic diagram of wellbore heat transfer physical model
钻井液从管内向下流动过程中,将与钻柱内壁发生对流换热;通过钻头喷嘴时,其温度变化为节流压降而产生的热量;在环空上返过程中,与井壁(或套管内壁)和钻柱外壁以热对流方式交换热量;在沿海水段隔水管环空上返过程中,流体将与隔水管内壁和钻柱外壁以热对流方式交换热量。地层中为二维瞬态传热,而海水与隔水管外壁之间为对流换热。
井筒内流体流动的自身产热和外界环境是影响环空内流体和井筒温度的主要因素,根据海上超高温高压钻井的特点,划分为3 个区域进行传热分析:1)钻柱段,环空内流动的流体为其外界环境;2)海底泥线以下的环空段,将与外部环境(地层和钻柱外壁)同时传热;3)隔水管环空段,其外部环境是海水。
2 钻井温度压力场耦合数学模型
模型建立过程中的基本假设为:1)假设在正常钻井工况中井筒内只存在单相流体钻井液;2)忽略井筒内流体的轴向导热,井筒内流体为一维瞬态传热;3)只考虑地层的热传导,且地层为瞬态传热;4)管柱内壁和外壁之间的传热忽略热阻的影响;5)流体和地层岩石的比热和导热系数不受温度、压力的影响;6)假设井筒内流体服从赫巴(Herschel-Bulkley)流变模式。
2.1 井筒传热控制方程
按照钻井井筒传热物理模型中划分的3 个传热区域,分别对每段传热区域进行控制方程分析,在循环过程,其流动符合动量守恒方程和连续性方程。
1)由质量守恒方程,可得连续性方程如式(1)所示:
式中:ρ为密度,kg/m3;v为流速,m/s;t为时间,s;A为流道的横截面积,m2;z为井筒轴线长度,m;下标i表示传热分析的第i部分。
2)由流体力学理论,可得动量方程如式(2)所示:
式中:p为压力,Pa;g 为重力加速度,m/s2;pf为摩阻压降,Pa。
2.2 循环期间传热数学模型
2.2.1 钻柱段传热模型
海水段井筒传热模型如图2所示,钻井液在沿钻柱向下流动过程将与钻柱内壁发生对流换热,钻柱外部为环空循环流动的钻井液。由传热学理论,可得钻柱内的温度场方程如式(3)所示:

图2 海水段井筒传热模型Fig.2 Wellbor e heat transfer model in seawater section
式中:ρf为钻井液的密度,kg/m3;cf为钻井液的比热容,J/(kg·℃);Tp为钻柱内温度,℃;Dpi为钻柱内径,m;Qf为钻井液排量,m3/s;qap为钻井液与环空或海水的换热量,J;qp为钻柱内摩阻产生的热量,J。
根据对流换热原理,环空中流动钻井液将与钻柱中流动钻井液交换热量,其径向对流换热量qap如式(4)所示:
式中:Ta为环空内温度,℃;Dpo为钻柱外径,m;hpi为钻柱内流体对流换热系数,W/(m2·℃);hpo为钻柱外流体对流换热系数,W/(m2·℃);qap为环空内钻井液与钻杆内钻井液之间的换热量,J。
2.2.2 环空段传热模型
1)海底泥线以下环空段
海底泥线以下环空内温度受到地层或套管内壁和钻柱外壁温度的影响,其井筒传热模型如图3所示。

图3 海底泥线以下井段井筒传热模型Fig.3 Wellbore heat transfer model below subsea mudline
钻井液在沿环空向上流动的过程中,与地层或套管内壁和钻柱外壁均发生对流换热,取流动方向为正方向,该段环空温度场方程如式(5)所示:
式中:Dai为环空内径,m;qea为地层和环空之间的换热量,J;qa为环空内摩阻产生的热量,J。
环空内钻井液与套管内壁或井壁发生对流换热,地层和水泥环内的传热为热传导,为了简化计算,可通过无因次时间函数f(t)来表示,可得井筒环空与地层之间的传热量qea如式(6)所示:
式中:Te为地层温度,℃;ke为地层导热系数,W/(m2·℃);kcem为水泥环导热系数,W/(m2·℃);Dh为水泥环外径,m;Dao为环空外径,m;hai为环空内流体对流换热系数,W/(m2·℃)。
2)隔水管环空段
隔水管环空段温度场的计算公式同式(5)相同。隔水管的外部环境为钻柱和海水,将与海水和钻柱内的流体都发生热交换,可得环空内钻井液与海水的对流换热量计算公式如式(7)所示:
式中:qsa为钻井液与海水的换热量,J;Tsea为海水的温度,℃;Dro为隔水管外径,m;Dri为隔水管内径,m;hro为隔水管外流体对流换热系数,W/(m2·℃);hri为隔水管内流体对流换热系数,W/(m2·℃);kr为隔水管导热系数,W/(m2·℃)。
2.3 井筒循环压耗计算模型
钻井液循环过程中,通过钻井液流态计算摩阻系数,得到循环摩阻,同时考虑钻头压耗及重力的影响,即可计算得到整个井筒压力分布。摩阻系数采用Blasius型经验计算公式[23]如式(8)所示:
式中:f为摩阻系数;Re为雷诺数;a′,b′为摩阻系数常数。
当钻井液流动处于层流状态时,a′=24,b′=1;当钻井液流动处于紊流状态时,系数a′和b′由流性指数决定,如式(9)所示:
式中:n 为流性指数。
循环过程的摩阻压耗如式(10)所示:
式中:Δpf为循环摩阻压耗,Pa;vf为钻井液流速,m/s;L 为井筒长度,m;d 为当量直径,m。钻头压耗如式(11)所示:
式中:Δpb为钻头压耗,Pa;cb为喷嘴流量系数;Ao为钻头喷嘴的当量面积,m2。
2.4 高温高压钻井液密度和流变参数模型
2.4.1 钻井液密度计算模型
由于流体的密度会受到温度压力的影响,因此应结合循环的温度场来计算温度压力对钻井液密度的影响,钻井液密度计算模型如式(12)所示[24]:
式中:ρf0为参考密度,kg/m3;p0为参考压力,Pa;T0为参考温度,℃;a,b,c为钻井液密度的特性系数;T为温度,℃;p为压力,Pa。
2.4.2 钻井液流变参数计算模型
在高温高压条件下,钻井液流变曲线近似为1 条曲线且不经过原点,而赫巴流变模式因为其综合幂律和宾汉2 种流变模式,能更好地描述钻井液在高温高压条件下的流动特性,因此钻井液流变模式采用Herschel-Bulkley模型[25-26]描述,赫巴流变模式表达式如式(13)所示:
式中:τ为剪切应力,Pa;τ0为屈服值,Pa;K为稠度系数,Pa·sn;γ为剪切速率,s-1。
从温度与压力条件对钻井液赫巴流型流变参数的影响进行分析,建立温度、压力条件对钻井液屈服值、稠度系数和流性指数影响的数学模型如式(14)所示[27]:
式中:f(ζ)可分别代表τ0,K和n;f(ζ0)为参考τ0,K和n;Aζ,Bζ,Cζ为钻井液流变参数的特性系数。
3 耦合数学模型的求解
3.1 边界条件
1)在井口,地表温度和注入钻井液温度为已知温度,钻井液出口压力等于大气压力。
2)在井底,钻柱内的温度与环空温度相等。
3.2 初始条件
海底泥线以上的井筒温度等于海水温度,如式(15)所示:
海底泥线以下的井筒温度等于地层温度,如式(16)所示:
3.3 求解算法
首先进行井筒空间离散化,确定网格时间、空间和径向的步长,时间域包含求解过程计算的整个时间段,空间域包含整个环空和钻柱节点,通过离散求解模型[28],再不断迭代求解耦合模型,计算井筒内温度压力剖面,其求解流程如图4所示。

图4 井筒温度压力场耦合模型求解流程Fig.4 Solution process of wellbore temperatur e and pressure field coupling model
4 超高温高压井实例计算
以海上某超高温高压井(D井)为例进行分析,该井水深90 m,钻井液入口温度为33 ℃,钻井液排量为16 L/s,地温梯度4.1 ℃/100m,海面温度为25 ℃。钻具组合为:Ø215.9 mm PDC钻头+高温阀芯浮阀+LWD+MWD+Ø206.4 mm倒划眼扶正器+堵漏短节+Ø165.1 mm钻铤×13 根+Ø165.1 mm震击器+411*520 转换接头+Ø139.7 mm加重钻杆×14 根+521*HT38 转换接头+Ø101.6 mm钻杆×1 500 m+HT38*520 转换接头+Ø139.7 mm钻杆。D井井身结构基础数据如表1所示,井筒内各单元的物理性质如表2所示。

表1 井身结构基础数据Table 1 Basic data of wellbore structure

表2 井筒内各单元的基础数据Table 2 Basic data of each wellbor e unit
4.1 井筒温度压力耦合变化规律
根据所建立的温度压力场耦合计算模型,计算温度和ECD耦合计算结果,与实例井现场随钻数据进行对比,以验证计算结果的准确性,实例井温度和ECD耦合计算结果与实测值对比如图5所示。
由图5可知,钻井液出口温度的计算值和实测值的最大误差为4.85%,ECD的计算值和实测值的最大误差仅为0.97%,表明本文模型计算精度较高。

图5 实例井温度和ECD耦合计算结果与实测值对比Fig.5 Comparison between coupling calculation results and measured values of temperature and ECD of example well
基于基础数据进行井筒温度压力耦合计算后,得到井筒温度剖面分布情况如图6所示,井筒压力分布情况如图7所示。
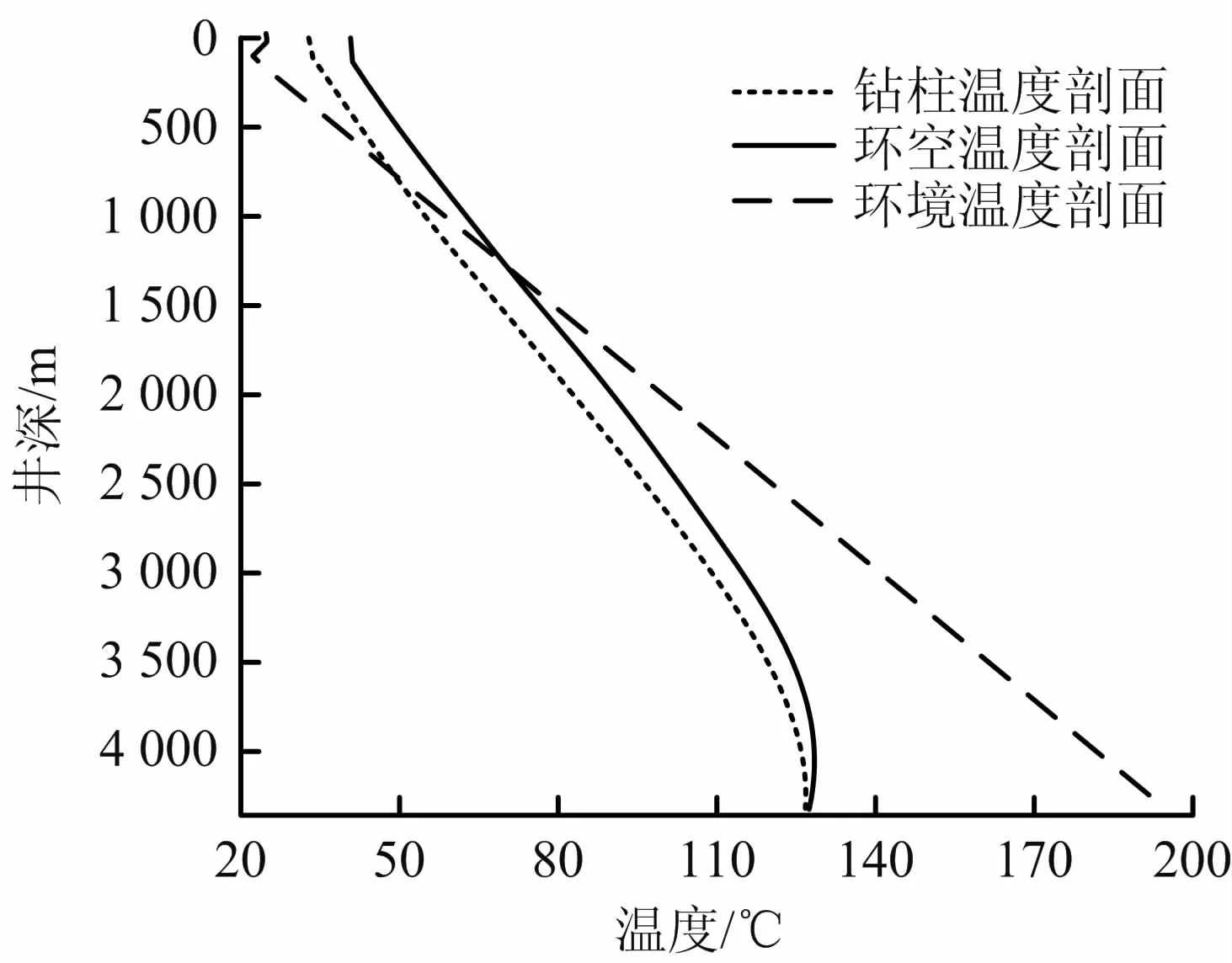
图6 井筒温度剖面分布情况Fig.6 Pr ofile distribution of wellbore temperature

图7 井筒压力的分布情况Fig.7 Distribution of wellbore pressure
由图6中可以看出,由于地层高温的影响,环空和钻柱内钻井液的温度差值比较小,钻柱和环空井底处温度值均为127.56 ℃;钻井液在上返流动过程中,环空温度值将先增加后降低,井深为4 060 m时达到最高温度128.50 ℃,这是由于钻井液在沿环空向上流动过程受到地层温度影响,将持续吸收地层热量,直到传递给钻杆的热量与从地层吸收的热量达到平衡,环空内钻井液将达到最高温度值。由图7可知,在同一井深处对应钻柱和环空内压力值,在井底处钻柱和环空内压力值基本相等;但在井口处钻柱和环空内压力差值为12.13 MPa。
4.2 钻井液的物性参数变化对耦合结果的影响
4.2.1 对井筒温度的影响
由于高温高压下钻井液性能的变化将对井筒温度场产生影响,分别计算考虑温压对钻井液密度的影响、考虑温压对钻井液流变性的影响、不考虑温压对钻井液物性参数的影响、同时考虑温压对钻井液密度和流变性的影响4 种条件下的井筒温度分布大小,如图8所示,其中同一线型,左侧表示钻柱温度在不同条件下随井深的变化,右侧表示环空温度随井深的变化。
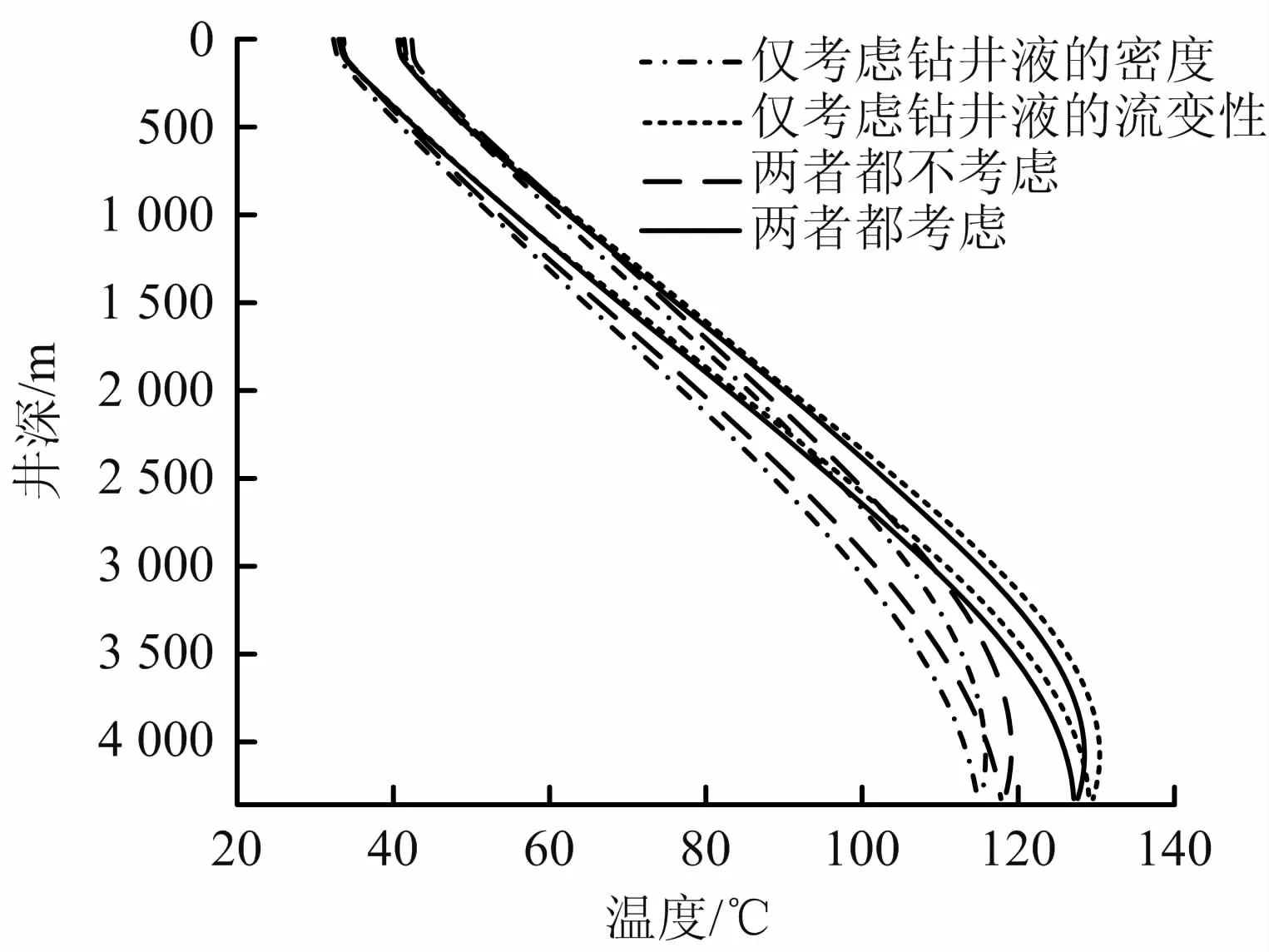
图8 钻井液性能对井筒温度场的影响Fig.8 Influence of drilling fluid perfor mance on wellbore temperature field
由图8可知,综合考虑温度压力对钻井液物性参数影响作用所得井筒温度,大于不考虑温度压力对钻井液物性参数影响作用时的井筒温度,且两者之间的误差随井深的增加越来越大,相对于上部浅层段,下部地层段受到的影响大,而在井底两者温度计算结果差值高达13 ℃;此外,钻井液流变性变化对井筒温度的影响大于钻井液密度变化的影响。因此,超高温高压钻井过程中进行井筒温度场预测时,应综合考虑钻井液性能受温度压力的影响。
4.2.2 对井筒压力的影响
考虑温度压力对钻井液性能的影响作用,计算得到井底压力随循环时间的变化规律如图9所示。
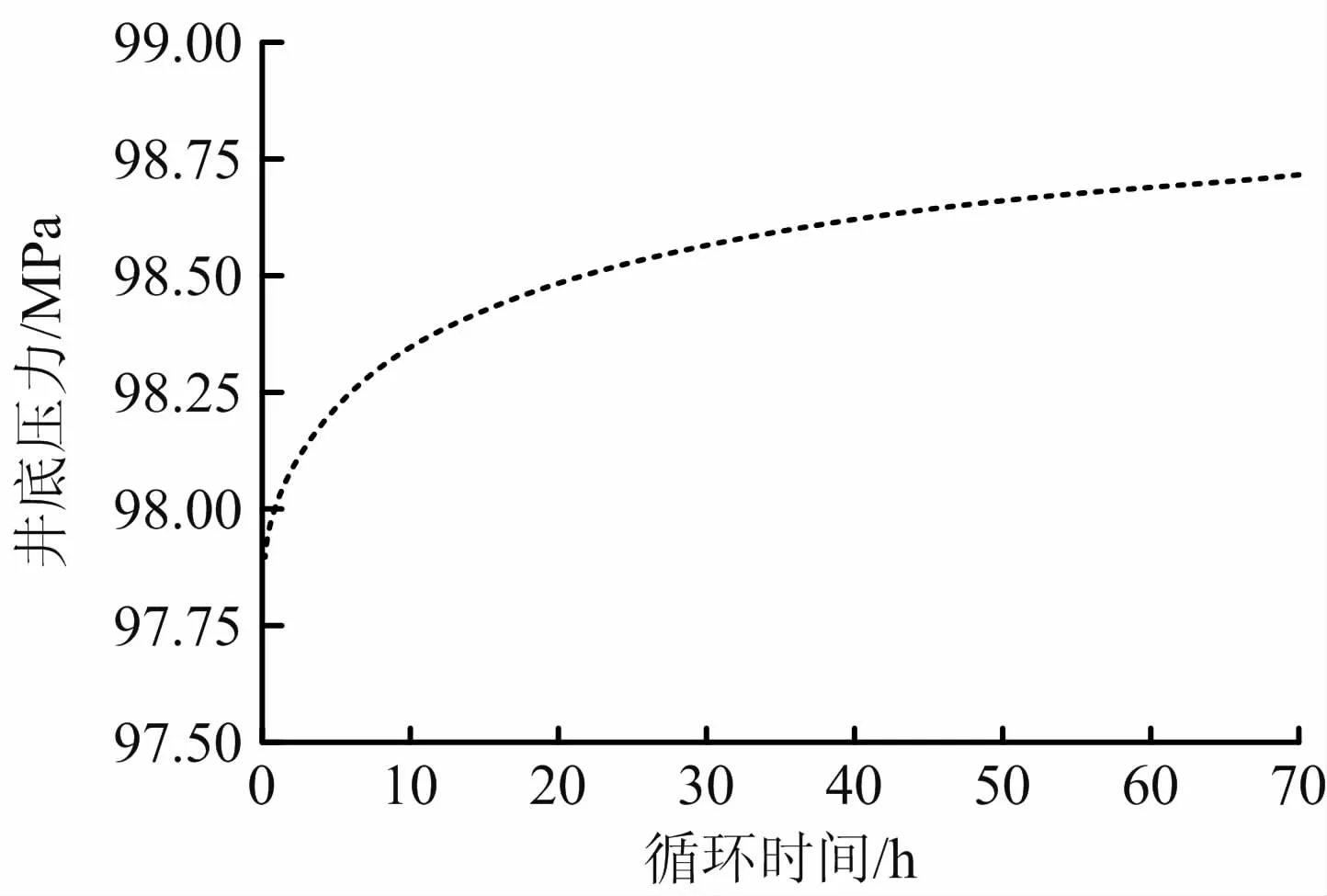
图9 井底压力随循环时间的变化规律Fig.9 Change of bottomhole pressure with circulation time
由图9可知,在开始循环时井底压力将随着循环时间的增加而逐渐增加,循环一定时间后井底压力将趋于稳定。在刚开始循环时间段,井底压力上升速度较快,是由于刚循环时井底温度高,钻井液平均温度值较高,钻井液平均密度较低;随着循环时间的增加,钻井液平均温度值明显降低,钻井液的平均密度和流变性增加,因此井底压力也逐渐增加;随着循环时间的增加,井筒内温度场逐渐达到平衡,井底压力逐渐稳定。
4.2.3 对密度的影响
分别计算考虑温度、压力及温度压力综合对钻井液密度的影响,得到钻进循环时不同井深处钻井液密度的分布情况如图10所示,其中同一线型,左侧表示环空内钻井液密度在不同条件下随井深的变化,右侧表示钻柱内钻井液密度变化。

图10 温度和压力对钻井液密度的影响Fig.10 Influence of temperature and pressure ondrilling fluid density
由图10可知,温度对钻井液密度的影响大于压力对钻井液密度的影响;仅考虑温度影响时,不同井深处钻井液密度均小于入口密度值,且在地层段受高温的影响钻井液密度明显小于入口密度值;而仅考虑压力影响时,钻井液密度大于入口密度值,且随井深逐渐增加。因此,若采用钻井液入口处的密度预测井底压力会产生较大误差,在实际预测中应综合考虑温度压力对钻井液密度的影响进行井底压力求解。
4.2.4 对ECD的影响
分别计算考虑密度、流变性及密度流变性综合对当量循环密度ECD的影响,得到不同井深处ECD的变化对比情况如图11所示。

图11 不同井深处ECD的变化对比情况Fig.11 Comparison of ECD change at different well depths
由图11可知,仅考虑温度压力作用下钻井液密度对ECD的影响程度大于流变性对ECD的影响;仅考虑密度变化的ECD明显低于两者都未考虑时的ECD;而仅考虑流变性变化的ECD 略低于两者都考虑时的ECD。计算结果表明,考虑密度和流变性两者变化对钻井液影响的ECD比两者变化都不考虑时的ECD低,相当于井底压力相差0.93 MPa,这对超高温高压窄安全密度窗口地层压力控制有很大的影响。因此,在海上超高温高压钻井过程中,有必要综合考虑温度压力对钻井液密度和流变参数的影响,耦合求解预测井筒温度压力场,以降低超高温高压地层窄密度窗口中的安全钻进风险。
5 结论
1)基于流体力学和传热学理论,综合考虑超高温高压井筒环境对钻井液密度以及钻井液流变参数的影响,建立海上超高温高压钻井井筒温度和压力耦合预测模型,分析钻井液循环期间井筒温度压力的变化规律。
2)对于井筒温度而言,钻井液流变性变化的影响大于钻井液密度变化的影响,耦合计算温度结果要大于不耦合计算的温度值,且两者之间的温差随井深的增加越来越大,两者温度差值在井底高达13 ℃。因此,在超高温高压钻井过程中进行井筒温度场预测时,应综合考虑钻井液性能受温度压力的影响。
3)对于钻井液密度而言,温度的升高将降低钻井液密度,而压力的升高将增加钻井液密度,但温度对钻井液的影响大于压力对钻井液密度的影响,因此在实际预测中应综合考虑温度压力对钻井液密度的影响进行井底压力求解。
4)而对于井筒压力而言,钻井液密度变化对ECD的影响要大于流变性对ECD的影响,且耦合计算的ECD要小于不耦合计算的ECD,两者差值可达0.022 g/cm3。为降低窄密度窗口中的安全钻进风险,海上超高温高压钻井过程中预测井筒温度压力场时有必要综合考虑温度压力对钻井液密度和流变参数的影响。
